面试经典 222. 完全二叉树的节点个数
-
二叉树我最近刷的特别多,差不多快刷完了,但是有一种题型差点给我忽略了,那就是完全二叉树,这也是一个很重要的题型,今天刚好有一道题目可以来复习一下完全二叉树的特性
-
题目链接如下:https://leetcode.cn/problems/count-complete-tree-nodes/?envType=study-plan-v2&envId=top-interview-150

-
做这道题首先有一点要知道的,就是完全二叉树是怎么样子的,下面说一下完全二叉树的概念
-
完全二叉树:只有最底层的节点未被填满,且最底层节点尽量靠左填充

-
ok 现在已经了解了基础概念了,我们再来看这道题目
-
这道题目的目的是让我们遍历这棵树,并算有几个节点
-
说实话,这道题很简单,用暴力的做法,就是遍历一整棵树,代码如下:
-
递归法:
//方法一:递归
func Solution222(root *TreeNode) int {if root == nil {return 0}left := Solution222(root.Left)right := Solution222(root.Right)return left + right + 1
}
- 迭代法:
//方法二:迭代
func Solution222v2(root *TreeNode) int {if root == nil{return 0}queue := []*TreeNode{root}count := 0for len(queue) > 0{node := queue[0]queue = queue[1:]count++if node.Left != nil{queue = append(queue, node.Left)}if node.Right != nil{queue = append(queue, node.Right)}}return count
}
-
这两个方法是遍历树的最基本的方法之一
-
但是 这不是这道题的本意,这道题目是想要我们理由完全二叉树这个特性解题
-
那我们需要好好思考一下,完全二叉树有什么特点
-
除了最后的叶子节点,其他层级节点都是满的
-
当 左子树的深度 和 右子树的深度 一致的时候,说明 左子树是满的二叉树 可以通过 2的h次方求的左子树的节点个数

-
当 右子树的深度 不如 左子树的深度 的时候,说明 左子树不是一个满的二叉树,但是右子树单独看是一个满的二叉树,所以可以通过 2的h次方求右子树的节点个数

-
-
ok,知道这些特点,我们是不是可以利用一个逻辑来减少遍历
- 当 左子树深度 等于 右子树的时候,就可以通过深度来计算左子树的节点,然后只遍历右子树
- 当 左子树深度 等于 右子树的时候,就可以通过深度来计算右子树的节点,然后只遍历左子树
-
这样我们本来需要遍历全部二叉树节点的,现在只需要遍历一半,思路瞬间打开,代码如下:
//方法三:二分查找
func Solution222v3(root *TreeNode) int {if root == nil{return 0}//检索左子树深度left := root.Leftldepth := 0for left != nil{left = left.Leftldepth++}//检索右子树深度right := root.Rightrdepth := 0for right != nil{right = right.Leftrdepth++}//左右子树深度判断if ldepth == rdepth{return (1<<ldepth) + Solution222v3(root.Right)}else{return (1<<rdepth) + Solution222v3(root.Left)}
}
ok,这里这道题目就结束了,感谢大家观看
相关文章:

面试经典 222. 完全二叉树的节点个数
二叉树我最近刷的特别多,差不多快刷完了,但是有一种题型差点给我忽略了,那就是完全二叉树,这也是一个很重要的题型,今天刚好有一道题目可以来复习一下完全二叉树的特性 题目链接如下:https://leetcode.cn/…...

【css】3d柱状图-vue组件版
创建一个响应式圆柱形进度条组件 在现代网页设计中,圆柱形进度条是一种非常流行的视觉元素,用于展示数据的进度或状态。本文将介绍如何使用Vue.js和LESS创建一个响应式的圆柱形进度条组件。 组件结构 我们的组件由两部分组成:一个圆柱形的…...

《计算机组成原理》(第3版)第3章 系统总线 复习笔记
第3章 系统总线 一、总线的基本概念 总线是连接多个部件的信息传输线,是各部件共享的传输介质,如图3-1所示。 图3-1 面向CPU的双总线结构框图 倘若将CPU、主存和I/O设备都挂到一组总线上,便形成单总线结构的计算机,如图3-2所示…...

【网络安全】https协议的加密方案避免中间人攻击(MITM攻击)导致的数据泄露风险
目录 引言 概念准备 中间人 加密 数据摘要 && 数据指纹 数字签名 密钥加密 中间人攻击 CA证书 https加密的解决方案 个人主页:东洛的克莱斯韦克-CSDN博客 引言 http在应用层协议中是明文传输协议,它是通信双方传输数据时的一种约定。【…...

拼多多商家电话采集 拼多多店铺爬虫软件使用教程
拼多多商家电话采集和店铺爬虫软件使用教程: 商家电话采集: a. 打开拼多多网站,进入需要采集电话号码的店铺页面。 b. 打开浏览器开发者工具(一般按F12键或右键选择“检查”)。 c. 在开发者工具中切换到“网络”或“Ne…...
RK3566 MIPI屏调试记录
文章目录 1. 前言2. 环境介绍3. 思路介绍4. 确认要修改的设备树文件5. 设备树中修改关键引脚5.1. 添加dsi0节点5.2. 修改屏幕背光引脚5.3. 添加屏幕复位引脚5.4. 添加屏幕使能引脚 6. 修改屏幕timing参数7. 修改上下电时序8. 修改初始化序列和反初始化序列9. 显示路由配置10. 最…...
)
爬虫数据模拟真实设备请求头User-Agent生成(fake_useragent:一个超强的Python库)
在Python开发中,处理HTTP请求时经常需要模拟不同的用户代理(User-Agent)来绕过网站的反爬虫机制或进行兼容性测试。fake_useragent正是这样一个强大的Python库,它能够生成随机且多样化的用户代理字符串,让你的请求看起…...

【教育宝-注册安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...
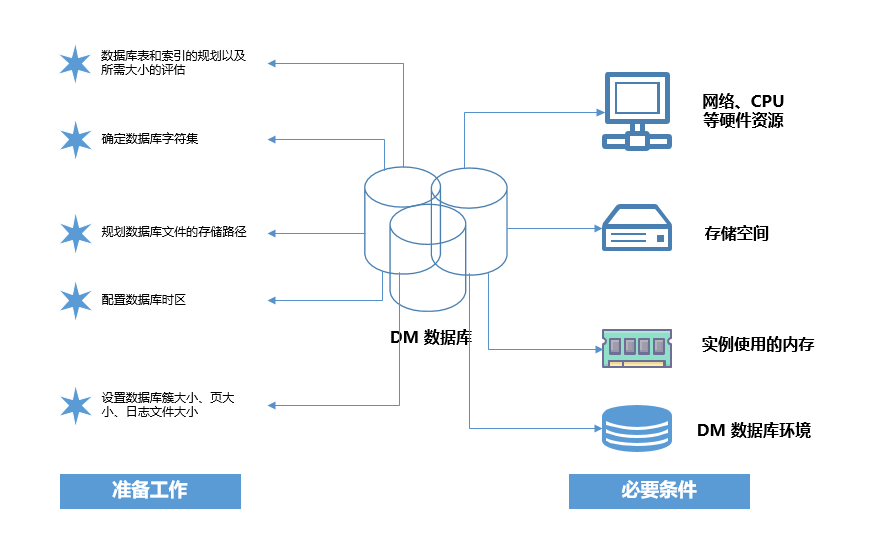
3.达梦数据库基础运维管理
文章目录 前言一、基础数据库管理权限角色管理1.1 DM 系统管理员的类型1.2 角色责则分类 DM 数据库2.1 数据库评估2.2 状态和模式 参考内容 前言 本篇博客为上一篇博客的进阶版,主要针对常规达梦数据库的基本管理上面 一、基础数据库管理 权限角色管理 1.1 DM 系…...

【Linux】【系统纪元】Linux起源与环境安装
快乐的流畅:个人主页 个人专栏:《C游记》《进击的C》《Linux迷航》 远方有一堆篝火,在为久候之人燃烧! 文章目录 一、Linux的起源1.1 计算机硬件1.2 计算机软件 二、Linux的环境安装2.1 安装方式2.2 安装版本2.3 安装过程2.4 远程…...
)
Android笔试面试题AI答之Activity(9)
文章目录 1.如何在Application中获取当前Activity实例 ?方法一:使用全局变量或单例方法二:使用LocalBroadcastManager或EventBus方法三:通过Fragment方法四:使用Service和Intent注意事项 2.Activity A跳转Activity B&a…...

什么是嵌入式
1、什么是嵌入式 对专用设备的控制,把不需要的功能能够裁剪、删除,适配于专用设备,就叫做嵌入式(也叫做嵌入式系统) 嵌入式系统定义:用于控制、监视或者辅助机器和设备的运行 一个嵌入式系统由硬件和软件…...

SAM 2:Segment Anything in Images and Videos 论文详解
SAM 2:Segment Anything in Images and Videos 文章目录 SAM 2:Segment Anything in Images and Videos摘要1 Introduction具体分析 2 Related work具体分析: 3 任务:可提示的视觉分割4 模型具体分析具体分析 5 数据5.1 Data engine5.2 SA - V数据集 6 Z…...
基操之我要玩并发)
PYTHON专题-(10)基操之我要玩并发
什么是并发? 并发指的是两个或多个事件在同一时间间隔内发生。在计算机科学中,并发通常指的是一个程序同时执行多个独立的任务。这些任务可以同时进行,而不会相互干扰或阻塞彼此。并发可以提高程序的执行效率和资源利用率,但也需要…...

双指针实现删除字符串中的所有相邻重复项
class Solution:def removeDuplicates(self, s: str) -> str:res list(s)slow fast 0length len(res)while fast < length:# 如果一样直接换,不一样会把后面的填在slow的位置res[slow] res[fast]# 如果发现和前一个一样,就退一格指针if slow …...

vue(vue2和vue3)项目打包去除console.log
1.Vue2去除 module.exports { configureWebpack: (config) > {// 取消console打印config.optimization.minimizer[0].options.terserOptions.compress.drop_console truereturn {name: "项目名称",resolve: {alias: {"": resolve("src")}}…...

Visual Studio 2022社区版、专业版、企业版功能对比表
https://visualstudio.microsoft.com/zh-hans/vs/compare/...

Codeforces 888 div3 A-G
A. Escalator Conversations 分析 二者身高差为k的倍数且不超过m-1倍,身高差不能为0(即不能在同一个阶梯) C代码 #include<iostream> using namespace std; void solve(){int n,m,k,H,ans0;cin>>n>>m>>k>>H;…...

IDEA如何去掉编辑框右侧的竖线
打开 IntelliJ Idea 软件 依次找到 File—>Settings—>Editor—>General—>Appearance 去掉勾选 Show hard wrap and visual guides (configured in Code Style options)...

3DCoat v2023 激活版下载与安装教程 (数字雕刻程序)
前言 3DCoat 是一款数字雕塑软件,由乌克兰开发。该软件专注于游戏模型的细节设计,集三维模型实时纹理绘制和细节雕刻功能为一身,可以加速细节设计流程,在更短的时间内创造出更多的内容。 一、下载地址 下载链接:分享…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
