直方图及其应用
直方图定义
直方图是一种描述数据的分布
通过将连续变量划分成一系列区间,统计区间频率,并用来表示,以表征其统计特征
在图像处理中,直方图可以用来表示图像中像素值的分布状况,描述不同灰度级的像素在图像中的占比

直方图应用
1. 图像增强。通过调整像素值,让图像的像素复合某种统计特性,达到增强图像的目的
2. 图像分割。利用直方图来将图像划分为多个区域,从而进行目标分割
3. 像素的统计特性,可以作为图像的一种特征,用于对图像内容进行分类、检索、压缩
https://blog.csdn.net/yishuihanq/article/details/120220374

OpenCV画直方图
cv2.calcHist(images,channels,mask,histSize,ranges)
关于`cv2.calcHist`函数的说明
hist = cv2.calcHist(images, channels, mask, histSize, ranges, accumulate)
- images: 源图像
- channels:参与计算直方图的通道
- mask:一个可选的掩膜,它与源图像具有相同的尺寸,用于指定计算直方图的区域。例如,可以通过指定一个矩形来计算图像的某个区域的直方图。
- histSize:表示要计算的直方图的大小,以方括号形式传入。如果输入图像是灰度图像,则为灰度级别数;如果是彩色图像,则可以对每个通道指定不同的大小,例如 [256, 256, 256] 表示每个通道的直方图大小为 256。
- ranges:表示像素值的范围,以方括号形式传入。如果输入图像是灰度图像,则范围应该是 [0, 256];如果是彩色图像,则可以为每个通道指定不同的范围,例如 [0, 256, 0, 256, 0, 256] 表示每个通道的范围分别为 [0, 256]。
- accmulate:一个可选的参数,用于指定是否要累加直方图。如果指定为 True,则计算整幅图像的直方图;如果指定为 False,则只计算当前区域的直方图。
2. (numpy)np.histagram
关于np.histagram的用法:
hist, bins = np.histogram(a, bins=10, range=None, normed=False, weights=None, density=None)
- a: 输入的一维数组。
- bins: 直方图的bin数量,也可以指定每个bin的边界,如[0, 10, 20, 30, 40]。
- range: 直方图统计的范围。
- normed和density:两个参数效果相同,设置是否对结果进行归一化。
对比度增强
对比度:最暗的像素和最大的像素值的对比
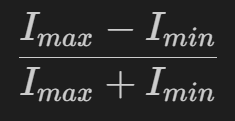
一个经典的对比度增强的方法:对比度拉伸,局限:仅适用于低动态图像
https://blog.csdn.net/xinjay1992/article/details/108672007

直方图均衡化
直方图最广泛的应用之一,就是直方图均衡化。
直方图均衡化,是一种对**图像增强**的方法:通过重新分配像素值的灰度级,来增强图像的对比度。
对于矩阵的意义:让像素在整个像素范围更加均匀
基本思想
将直方图变换为一个均匀分布的直方图,使得像素值更加均匀,从而达到增强图像的目的。
通常,直方图中呈现尖峰的位置,说明处于该值的像素较为接近
而直方图均衡化后,可以令这些像素取值更加分散,因此视觉上可以将不明显的物体与周围物体区分开来
计算过程
https://blog.csdn.net/weixin_45930877/article/details/119581282
直方图性质等详解:https://zhuanlan.zhihu.com/p/411042641
底层代码
np.interp 是 NumPy 中的一个函数,用于进行线性插值。具体来说,
np.interp(x, xp, fp, left=None, right=None, period=None) 函数用于计算一个新的数组 x 对应的线性插值结果。其中,x 表示需要进行插值的位置,xp 表示已知数据的位置,fp 表示已知数据的取值。
具体地说,np.interp 的计算方式为:对于 x 中的每一个位置,找到其在 xp 中的相邻位置 xp_i 和 xp_{i+1},然后在这两个位置的 fp 取值中进行线性插值,得到 x 对应位置的插值结果。
如果 x 中的某个位置超出了 xp 的取值范围,那么根据参数 left 和 right 的取值,有不同的处理方式。如果 left 和 right 都未指定,那么超出取值范围的位置将返回 np.nan;如果 left 和 right 中的一个指定了值,那么超出取值范围的位置将使用该值进行插值;如果两者都指定了值,那么会根据超出位置的方向分别使用两个值进行插值。
此外,如果 xp 中的值不是单调递增的,那么可以使用参数 period 指定数据的周期,从而进行周期性插值。
import cv2
import numpy as np
import matplotlib.pyplot as plt# 先把图像变暗
img = cv2.imread('E:/notebook/lena.png', 0)
plt.imshow(img, cmap='gray')
plt.show()
dark = (0.5 * img).astype('uint8')
# cv2.imwrite("E:/notebook/dark_lena.jpg", dark)
image = cv2.imread("E:/notebook./dark_lena.jpg")
plt.imshow(image, cmap='gray')
plt.show()
# 计算直方图
hist, bins = np.histogram(img.flatten(), 256, [0,256])
plt.hist(hist, bins=bins)
plt.show()
print(hist[100:105])
# [1950 1950 1881 1862 1683]
# 直方图归一化
hist_norm = hist.astype(np.float32) / hist.sum()
print(hist_norm[100:105])
# [0.00743866 0.00743866 0.00717545 0.00710297 0.00642014]
# 计算累积直方图
cum_hist = hist_norm.copy()
for i in range(1, len(cum_hist)):cum_hist[i] = cum_hist[i-1] + cum_hist[i]
print(cum_hist[100:105])
# [0.32024384 0.3276825 0.33485794 0.34196091 0.34838104]
# 均衡化
img_equalized = np.interp(img.flatten(), bins[:-1], cum_hist).reshape(img.shape)
# print(bins)
plt.imshow(img_equalized, cmap='gray')
plt.show()

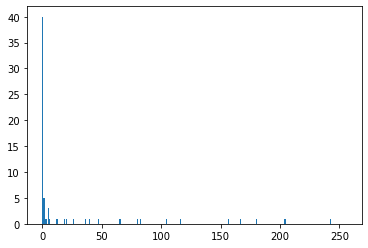

缺点
直方图整体均衡化用于增强图像质量。通过将图像映射到小区间,并进行归一化,使得其像素范围能够充斥整个空间。从而达到增强图像对比度,或者将亮度调整到适宜空间内的效果。
然而,对图像总体进行直方图均衡化,也会造成一些负面效果。
* 图像中某部分很亮,其他部分很暗,直方图均衡化会导致亮部过曝

* 图像分层

* 噪声问题
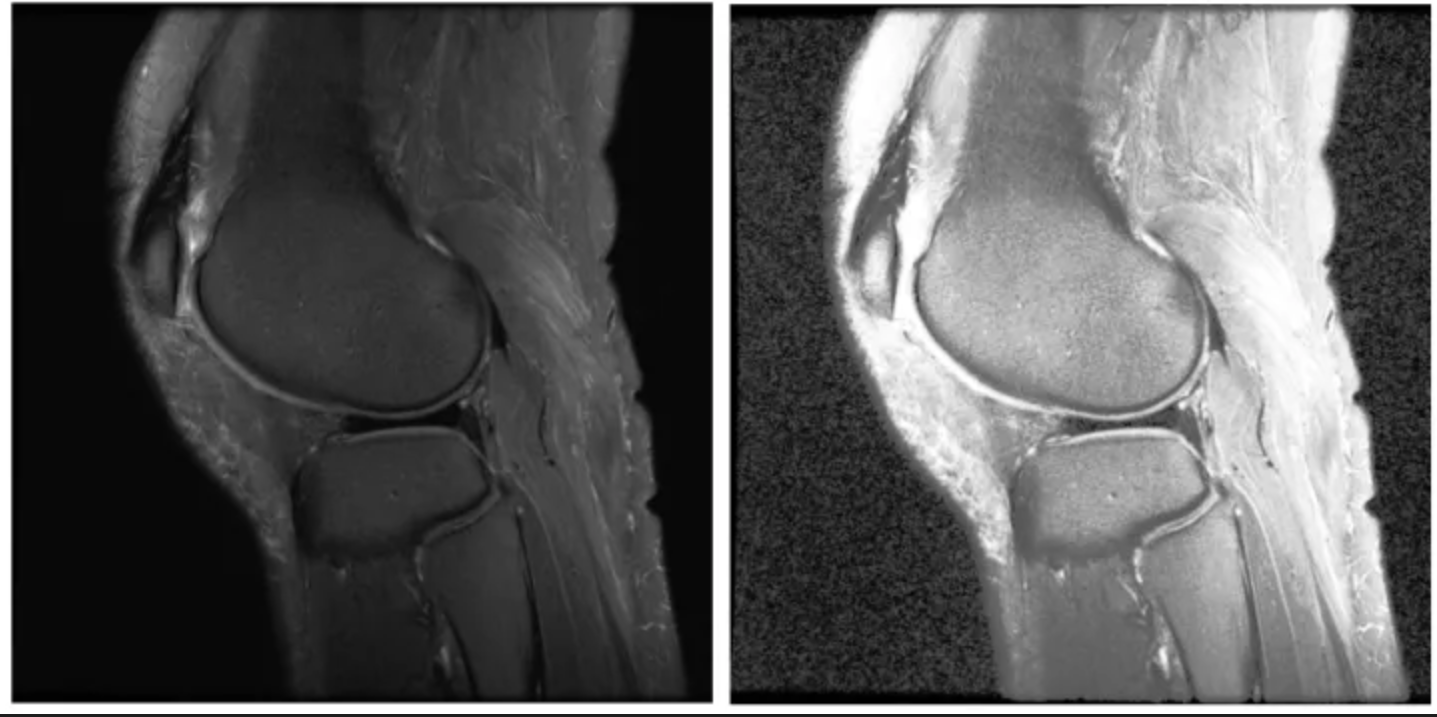
自适应直方图均衡(AHE, adaptive histogram equalization)
将图像分成若干的各区域,对每个小区域做直方图均衡化
def AHE(im, wsz=100):h, w = im.shapeout = np.zeros(im.shape) # Declare output variablefor x in range(wsz//2, h + wsz//2):for y in range(wsz//2, w + wsz//2):blk = im[x-wsz//2:x+wsz//2, y-wsz//2:y+wsz//2]tmp = cv2.equalizeHist(blk)out[x-wsz//2:x+wsz//2, y-wsz//2:y+wsz//2] = tmpreturn out
img = cv2.imread("E:/notebook/person.png", 0)
plt.imshow(img, cmap="gray")
plt.show()
img = AHE(cv2.imread("E:/notebook/person.png", 0), wsz=50)
plt.imshow(img, cmap="gray")
plt.show()

CLAHE (contrast limited adaptive histogram equalization)
**核心思想** 将图像划分为若干个小块,并在小块内进行限制性直方图均衡化,经双线性最后的均衡化后的图像。
**步骤**
1. 将图像划分成若干个大小相等的块
2. 对每个子图进行“限制性”均衡化
3. 插值,得到均衡化后的像素值
“限制性”均衡化
**参数解释**
`clipLimit`: 控制了直方图均衡化中对比度增强的程度。该参数的数值越大,对比度增强的程度也越大,但是同时也会增加图像出现伪影的概率。
clip_limit = clip_limit_factor * (M / N)
其中,clip_limit_factor是一个用户定义的参数,通常取值在0.01到0.1之间;M是图像像素数量,N是直方图中的最高峰的数量。通常情况下,N的取值在50到200之间。
import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
clip_limit = 5
arr_clipped = np.clip(arr, a_min=None, a_max=clip_limit)
print(arr_clipped)
# [1 2 3 4 5 5 5 5 5]平滑伪影
`tileGridSize` 表示将图像分割成的小块的大小。它对均衡化结果的影响主要体现在以下两个方面:
* 计算直方图时的像素点数量:由于 CLAHE 算法是在每个小块上进行直方图均衡化,因此 tileGridSize 的大小会直接影响每个小块中包含的像素点数量。如果 tileGridSize 太小,每个小块中的像素点数量就会很少,可能会导致直方图统计不准确,从而影响均衡化结果。而如果 tileGridSize 太大,每个小块中的像素点数量就会很多,可能会导致直方图过于集中,也会影响均衡化结果。因此,要根据具体的图像特征和处理需求,选择适当的 tileGridSize 大小。
* 均衡化效果的细节保留:tileGridSize 的大小还会影响均衡化结果中细节的保留程度。如果 tileGridSize 太小,每个小块中的像素点数量较少,可能会导致细节的损失。而如果 tileGridSize 太大,每个小块中的像素点数量较多,可能会导致一些小细节被平滑掉,从而导致细节不够清晰。因此,要根据具体的需求和图像特征,选择适当的 tileGridSize 大小,以达到最优的均衡化效果和细节保留程度。
cl = cv2.createCLAHE(clipLimit=3, tileGridSize=(8, 8))
im = cl.apply(cv2.imread("E:/notebook/person.png", 0))
plt.imshow(im, cmap='gray')
plt.show()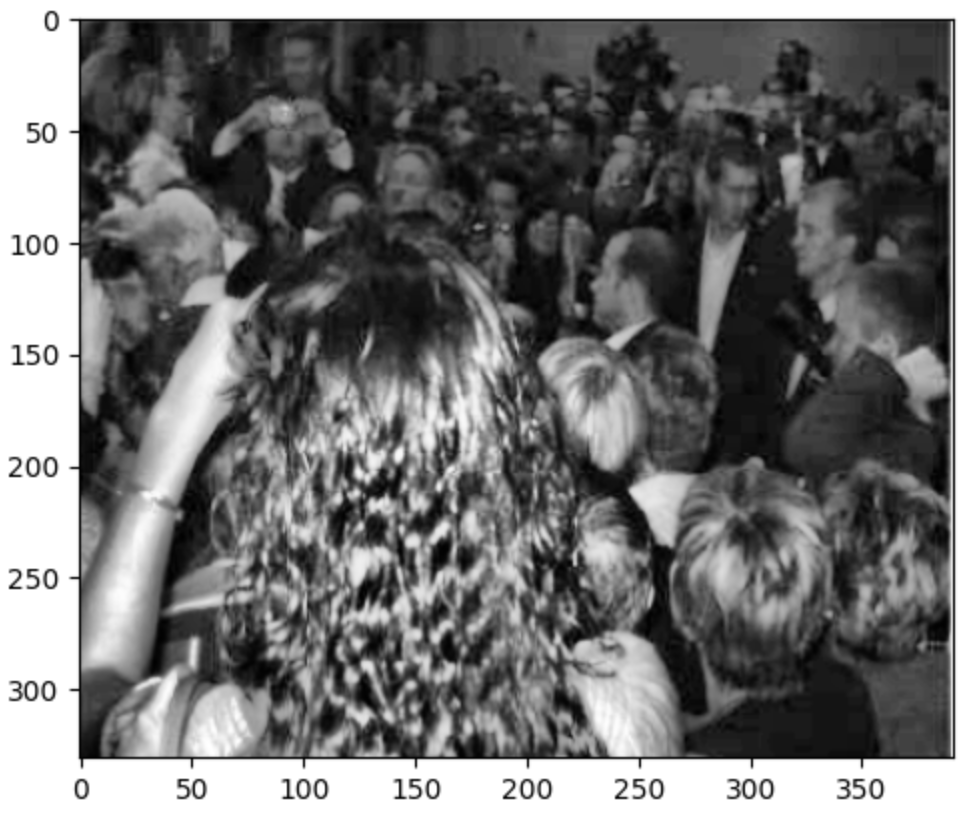
直方图应用---图像分割
直方图的波动曲线,表示了不同像素等级的统计信息
对于一个语义上关联较为紧密的物体,其像素的关联可能也较为紧密
因此,在对某个高频像素进行处理的时候,往往也是对于语义关联较为紧密的物体进行处理。
最优阈值怎么选?
img = cv2.imread('E:/notebook/greenscreen.png')
plt.imshow(img)
plt.show()
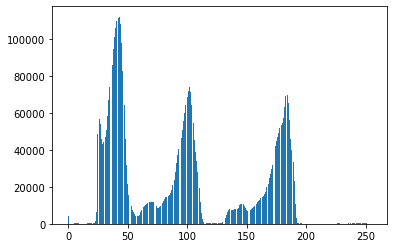
hist, bins = np.histogram(img.flatten(), 256, [0, 256])
print(hist)
plt.bar(range(256), hist.ravel())
plt.show()
max_peak = np.argmax(hist)
print(max_peak) # 最多的43阈值1
second_peak = np.argmin(hist[100: 150]) + 100
print(second_peak) # 第二多的119阈值2
# 区间1 [0: max]
img_bin = np.zeros_like(img)
img_bin = np.where((img >= max_peak), 255, img_bin)[:, :, 0]
plt.imshow(img_bin, cmap='gray')
plt.show()
img_bin_2 = np.ones_like(img) * 0
img_bin_2 = np.where((img <= second_peak), 255, img_bin_2)[:, :, 0]
plt.imshow(img_bin_2, cmap='gray')
plt.show()
mask = img_bin * img_bin_2
plt.imshow(mask, cmap='gray')
plt.show()
[ 4453 8 45 52 136 241 268 419 321 185
125 146 146 151 149 168 178 251 253 323
375 475 584 1422 6139 48787 56813 54050 46046 43175
44371 46881 50671 58219 67125 74001 79400 86139 94594 101315
106251 109673 111434 112107 108057 98107 82611 64185 45954 32076
21640 15553 11695 9372 7469 6331 5179 4293 4001 4069
4792 6236 7699 8896 9643 10292 10823 11433 11818 11658
11690 11837 11720 10725 9846 8624 8447 8868 9864 11090
12556 13322 14375 14455 14782 15375 16505 18185 20749 23972
27871 32725 37063 40653 43648 46654 50872 55540 60205 64409
68385 71674 73997 71533 64290 54777 45432 38829 34013 27982
19619 11758 5682 2464 1106 706 514 488 441 417
438 421 431 444 427 437 465 474 555 690
1209 2081 3344 4898 6402 7349 7833 7570 7398 7632
7893 8051 8164 8724 10058 10658 10922 10622 9631 8468
7228 6841 7235 7717 8257 8614 8938 9540 10613 11682
12396 12713 13697 14371 14911 16181 17299 19732 21809 24816
27204 29519 32065 37209 41996 45069 46880 49048 51798 53681
54753 57345 63271 69282 69754 65532 56153 46119 39935 33199
23103 10697 3033 681 246 182 183 124 108 104
86 100 81 95 73 84 79 86 81 73
81 106 119 131 119 125 113 124 128 132
142 126 157 133 129 142 181 169 183 140
100 82 100 93 107 150 169 182 145 195
250 318 440 511 573 544 426 427 376 354
276 230 161 115 110 95]



相关文章:

直方图及其应用
直方图定义直方图是一种描述数据的分布通过将连续变量划分成一系列区间,统计区间频率,并用来表示,以表征其统计特征在图像处理中,直方图可以用来表示图像中像素值的分布状况,描述不同灰度级的像素在图像中的占比直方图…...
《SpringBoot篇》26.SpringBoot整合Jackson超详细教程(附Jackson工具类)
陈老老老板🦸👨💻本文专栏:SpringBoot篇(主要讲一些与springboot整合相关的内容)👨💻本文简述:本文讲一下Jackson常见用法,超级详细。👨&am…...
Redis 如何实现库存扣减操作和防止被超卖?
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
Ubuntu查看系统版本)
(Linux)Ubuntu查看系统版本
uname -a : 查看操作系统的发行版号和操作系统版本 Command: uname -aResult: Linux SERVER 5.19.0-35-generic #36-Ubuntu SMP PREEMPT_DYNAMIC Fri Feb 3 18:36:56 UTC 2023 x86_64 x86_64 x86_64 GNU/Linux uname -v : 查看版本号 Command: uname -vResult: #36-Ubuntu …...
)
VxWorkds 内存管理(3)
虚拟内存管理 对于带MMU的目标板,VxWorks提供虚拟内存的支持,VxWorks提供了两种虚拟内存管理单元(MMU)的支持: 基本MMU和VxVMI 基本MMU邦定于VxWorks中,可以通过config.h中宏定义INCLUDE MMU BASIC或Tornado工程配置中包含基本MMU组件 VxV…...

单元测试、反射、注解、动态代理
🏡个人主页 : 守夜人st 🚀系列专栏:Java …持续更新中敬请关注… 🙉博主简介:软件工程专业,在校学生,写博客是为了总结回顾一些所学知识点 目录单元测试、反射、注解、动态代理单元测…...

【数据结构】夯实基础|线性表刷题01
作者:努力学习的大一在校计算机专业学生,热爱学习和创作。目前在学习和分享:算法、数据结构、Java等相关知识。博主主页: 是瑶瑶子啦所属专栏: 【数据结构|刷题专栏】:该专栏专注于数据结构知识,持续更新&a…...
Java怎么实现几十万条数据插入(30万条数据插入MySQL仅需13秒)
本文主要讲述通过MyBatis、JDBC等做大数据量数据插入的案例和结果。 30万条数据插入插入数据库验证实体类、mapper和配置文件定义User实体mapper接口mapper.xml文件jdbc.propertiessqlMapConfig.xml不分批次直接梭哈循环逐条插入MyBatis实现插入30万条数据JDBC实现插入30万条数…...
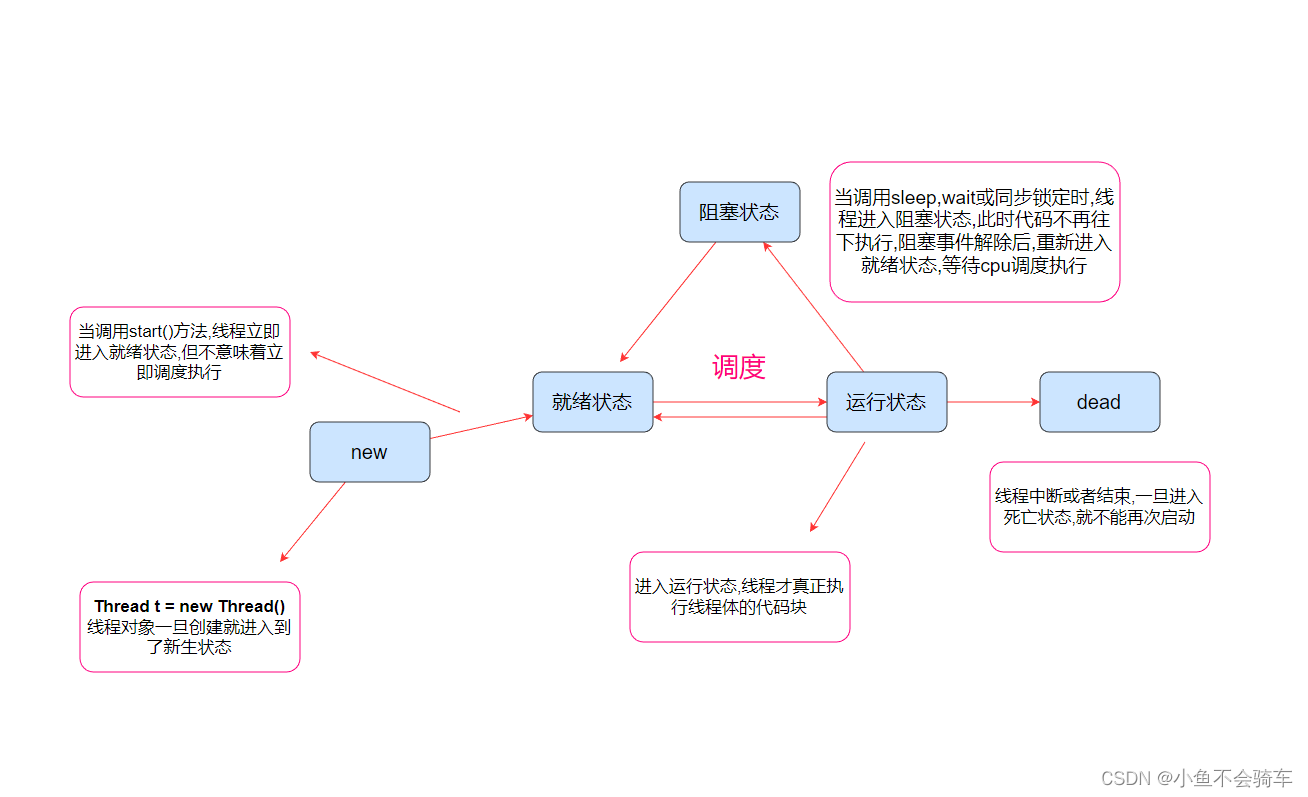
java多线程之线程的六种状态
线程的六种状态(1) NEW(初始状态)(2) TERMINATED(终止状态 / 死亡状态)(3) RUNNABLE(运行时状态)(4) TIMED_WAITING(超时等待状态)(5) WAITING(等待状态)(6) BLOCK(阻塞状态)sleep和wait的区别:操作系统里的线程自身是有一个状态的,但是java Thread 是对系统线程的封装,把这里的…...
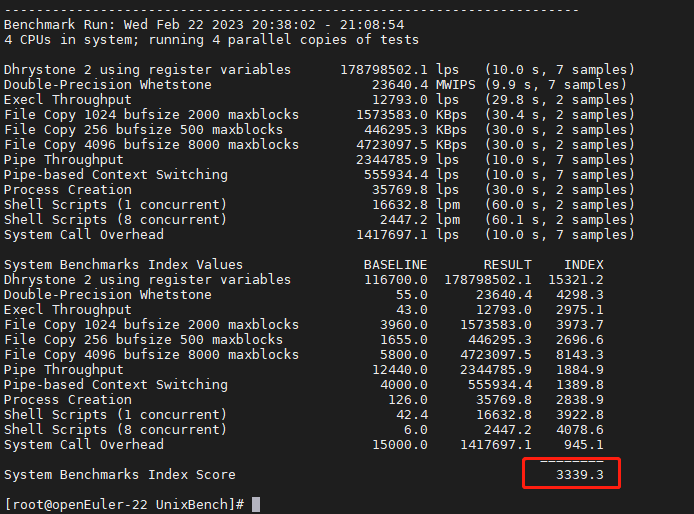
UnixBench----x86架构openEuler操作系统上进行性能测试
【原文链接】UnixBench----x86架构openEuler操作系统上进行性能测试 (1)打开github上 UnixBench 地址,找到发布的tag (2)找到tar.gz包,右键复制链接 比如这里是 https://github.com/kdlucas/byte-unix…...
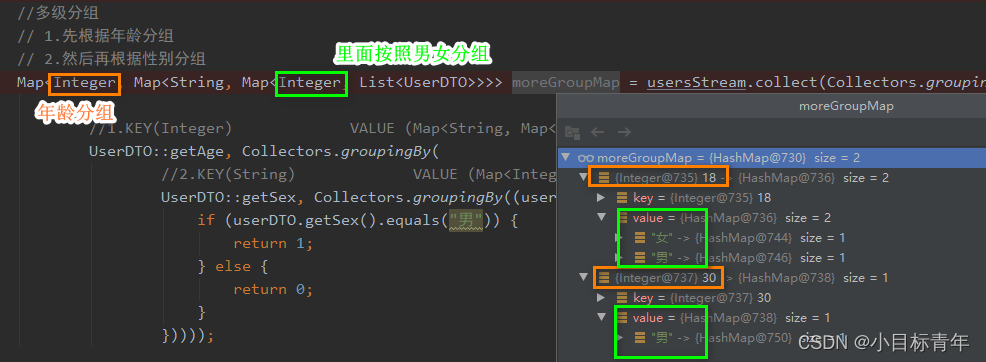
于Java8 Stream教程之collect()
目录 前言正文第一个小玩法 将集合通过Stream.collect() 转换成其他集合/数组:第二个小玩法 聚合(求和、最小、最大、平均值、分组)总结前言 本身我是一个比较偏向少使用Stream的人,因为调试比较不方便。 但是, 不得不说&#…...

Python
1、str 三个关键点: 正着数,0,1,2 反着数,0,-1,-2 str[a,b] 左闭右开 [a,b) str123456789 print(str) # 输出字符串 print(str[0:-1]) # 输…...
Spring框架中IOC和DI详解
Spring框架学习一—IOC和DI 来源黑马Spring课程,觉得挺好的 目录 文章目录Spring框架学习一---IOC和DI目录学习目标第一章 Spring概述1、为什么要学习spring?2、Spring概述【了解】【1】Spring是什么【2】Spring发展历程【3】Spring优势【4】Spring体系…...
本地快速搭建Kubernetes单机版实验环境(含问题解决方案)
Kubernetes是一个容器编排系统,用于自动化应用程序部署、扩展和管理。本指南将介绍Kubernetes的基础知识,包括基本概念、安装部署和基础用法。 一、什么是Kubernetes? Kubernetes是Google开发的开源项目,是一个容器编排系统&…...
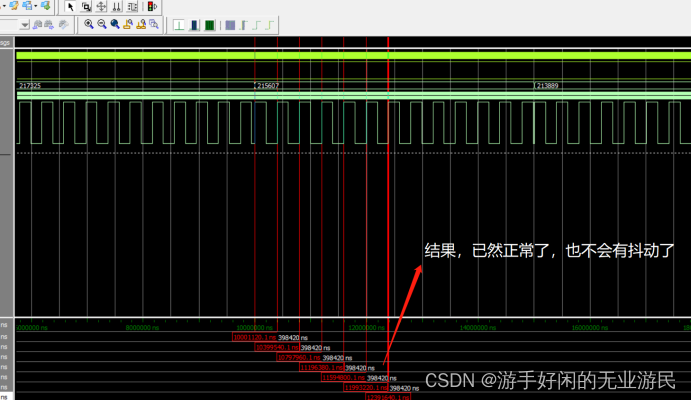
FPGA控制DDS产生1CLK周期误差的分析(二)
前文简短的介绍了DDS的产生原理,其实相当的简单,所以也不需要多做解释,本文详细阐述一下在调试DDS的过程中所产生的一个bug 问题发现 正如上文所述,再用FPGA控制存储在rom中的波形信号输出之后,在上板之前࿰…...

这一次,吃了Redis的亏,也败给了GPT
关注【离心计划】,一起离开地球表面 背景 组内有一个系统中有一个延迟任务的需求,关于延迟任务常见的做法有时间轮、延迟MQ还有Redis Zset等方案,关于时间轮,这边小苏有一个大学时候做的demo: https://github.com/JA…...

第一章 信息化知识
1、信息是客观事物状态和运动特征的一种普遍形式,信息的概念存在两个基本的层次,即本体论层次和认识论层次: 本体论层次:就是事物的运动状态和状态变化方式的自我表述认识论层次:就是主体对于该事物的运动状态以及状态…...
如何用matlab工具箱训练一个SOM神经网络
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》bp.bbbdata.com本文展示如何用matlab工具箱训练一个SOM神经网络的DEMO并讲解其中的代码含义和相关使用说明- 01.SOM神经网络DEMO代码 -- 本文说明 -下面,我们先随机初始化一些样本点,然后…...

音视频技术开发周刊 | 285
每周一期,纵览音视频技术领域的干货。新闻投稿:contributelivevideostack.com。GPT-4 Office全家桶发布谷歌前脚刚宣布AI工具整合进Workspace,微软后脚就急匆匆召开了发布会,人狠话不多地祭出了办公软件王炸——Microsoft 365 Cop…...

安装flume
flume最主要的作用就是实时读取服务器本地磁盘的数据,将数据写入到hdfs中架构:开始安装一,上传压缩包,解压并更名解压:[rootsiwen install]# tar -zxf apache-flume-1.9.0-bin.tar.gz -C ../soft/[rootsiwen install]#…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
