跳跃-动态规划问题
跳跃-动态规划问题
- 1、题目描述
- 2、解题思路
- 2.1 解法一:动态规划
- 2.2 解法二:DFS深度优先搜索最大权值
1、题目描述
小蓝在一个 n 行 m 列的方格图中玩一个游戏。
开始时,小蓝站在方格图的左上角,即第 11 行第 11 列。
小蓝可以在方格图上走动,走动时,如果当前在第 r 行第 c* 列,他不能走到行号比 r 小的行,也不能走到列号比 c 小的列。同时,他一步走的直线距离不超过 3。
例如,如果当前小蓝在第 3 行第 5 列,他下一步可以走到第 3 行第 6 列、第 3 行第 7 列、第 3 行第 8 列、第 4 行第 5 列、第 4 行第 6 列、第 4 行第 7 列、第 5 行第 5 列、第 55 行第 6 列、第 6 行第 5 列之一。
小蓝最终要走到第 n 行第 m 列。
在图中,有的位置有奖励,走上去即可获得,有的位置有惩罚,走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值,奖励为正,惩罚为负。
小蓝希望,从第 1 行第 1 列走到第 n 行第 m* 列后,总的权值和最大。请问最大是多少?
输入描述
输入的第一行包含两个整数 n,m,表示图的大小。
接下来 n 行,每行 m* 个整数,表示方格图中每个点的权值。
其中,1≤n≤100,−104≤权值≤1041\le n\le 100,-10^4\le 权值\le10^41≤n≤100,−104≤权值≤104
输出描述
输出一个整数,表示最大权值和。
输入输出样例
示例 1
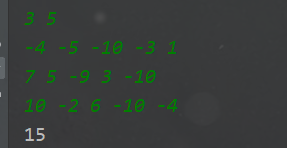
输入
3 5
-4 -5 -10 -3 1
7 5 -9 3 -10
10 -2 6 -10 -4
输出
15
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
2、解题思路
2.1 解法一:动态规划

开始的时候我们站在(1,1)(1,1)(1,1)位置,且一步走的直线距离不超过3,如上图所示,假设我们现在开始在(1,1)(1,1)(1,1)位置,那么我们下一步的位置只能是(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)其中的一个。
那我们可以由此建立一个搜索的坐标数组,每次从当前位置搜的时候我们就扩展坐标即可。
令dp[i][j]dp[i][j]dp[i][j]表示从(1,1)(1,1)(1,1)到达(i,j)(i,j)(i,j)位置获得的最大权值。
但是我们当前位置是由前面九个位置决定的,所以我们需要将上面的坐标反推回去。
(−1,−2),(−1,−3),(−1,−4),(−2,−1),(−2,−2),(−2,−3),(−3,−1),(−3,−2),(−4,−1)(-1,-2),(-1,-3),(-1,-4),(-2,-1),(-2,-2),(-2,-3),(-3,-1),(-3,-2),(-4,-1)(−1,−2),(−1,−3),(−1,−4),(−2,−1),(−2,−2),(−2,−3),(−3,−1),(−3,−2),(−4,−1)
那么我们建立一个扩展的坐标数组
//当前位置只能由前面9个位置到达,所以都填了负号public static int[][] dirs={{0,-1},{0,-2},{0,-3},{-1,0},{-1,-1},{-1,-2},{-2,0},{-2,-1},{-3,0}};
每搜索到一个节点(x,y),就判断当前的dp[i][j]和dp[x][y]+a[i]哪个大即可,状态转移方程如下:
dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j])dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j]) dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j])
完整代码实现:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
//dp[i][j]表示从(1,1)到达(i,j)位置获得的最大权值
public class Main {//当前位置只能由前面9个位置到达,所以都填了负号public static int[][] dirs={{0,-1},{0,-2},{0,-3},{-1,0},{-1,-1},{-1,-2},{-2,0},{-2,-1},{-3,0}};public static StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));public static void main(String[] args) throws IOException {int n = nextInt();int m = nextInt();int[][] a = new int[n + 1][m + 1];int[][] dp = new int[n + 1][m + 1];for (int i = 1; i <=n; i++) {for (int j = 1; j <=m ; j++) {a[i][j]=nextInt();}}for (int[] ints : dp) {Arrays.fill(ints,Integer.MIN_VALUE);}dp[1][1]=a[1][1];//初始化for (int i = 1; i <=n ; i++) {for (int j = 1; j <=m; j++) {for (int k = 0; k <9; k++) {//9个位置扩展//扩展int x = i + dirs[k][0];int y = j + dirs[k][1];if(x>=1&&x<=n&&y>=1&&y<=m){ //判断是否越界dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j]);}}}}System.out.println(dp[n][m]);}public static int nextInt() throws IOException {st.nextToken();return (int)st.nval;}
}

2.2 解法二:DFS深度优先搜索最大权值
使用深度优先遍历,我们对可扩展的方向进行DFS,每次找到终点(n,m)(n,m)(n,m)的时候我们就更新一下最大权值即可。
但是请注意,现在我们是从左上往右下走,所以坐标是正的,此时扩展的方向数组为:
//这里是往右下方向走,所以坐标都是正的public static int[][] dirs={{0,1},{0,2},{0,3},{1,0},{1,1},{1,2},{2,0},{2,1},{3,0}};
完整代码如下:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main {//这里是往右下方向走,所以坐标都是正的public static int[][] dirs={{0,1},{0,2},{0,3},{1,0},{1,1},{1,2},{2,0},{2,1},{3,0}};public static int n;public static int m;public static int[][] a;public static int cnt=0;public static StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));public static void main(String[] args) throws IOException {n = nextInt();m = nextInt();a = new int[n + 1][m + 1];for (int i = 1; i <=n; i++) {for (int j = 1; j <=m ; j++) {a[i][j]=nextInt();}}dfs(1,1,a[1][1]);System.out.println(cnt);}public static void dfs(int x,int y,int res){if(x==n&&y==m){ //到达终点之后,更新权值和cnt=Math.max(cnt,res);return;}//开始扩展for (int[] dir : dirs) {//(x,y)下一个位置的坐标(ex,ey)int ex = x + dir[0];int ey = y + dir[1];if(ex>=1&&ex<=n&&ey>=1&&ey<=m){ //判断是否越界dfs(ex,ey,res+a[ex][ey]);}}}public static int nextInt() throws IOException {st.nextToken();return (int)st.nval;}
}
这道题有点类似于那个数字三角形,那个题是只能往右边或者下边走,同样反推回去建立可扩展的坐标数组即可。
相关文章:

跳跃-动态规划问题
跳跃-动态规划问题1、题目描述2、解题思路2.1 解法一:动态规划2.2 解法二:DFS深度优先搜索最大权值1、题目描述 小蓝在一个 n 行 m 列的方格图中玩一个游戏。 开始时,小蓝站在方格图的左上角,即第 11 行第 11 列。 小蓝可以在方格…...

Django笔记三十九之settings配置介绍
这一篇笔记介绍 Django 里 settings.py 里一些常用的配置项,这些配置有一些是在之前的笔记中有过介绍的,比如 logging 的日志配置,session 的会话配置等,这里就只做一下简单的回顾,有一些是之前没有介绍过的就着重介绍…...
【JavaSE】类和对象(中)
类和对象(中)4. this引用4.1 为什么要有this引用4.2 什么是this引用4.3 this引用的特性5. 对象的构造及初始化5.1 如何初始化对象5.2 构造方法(构造器)5.2.1 概念5.2.2 特性5.3 默认初始化5.4 就地初始化6. 封装6.1 封装的概念6.2…...
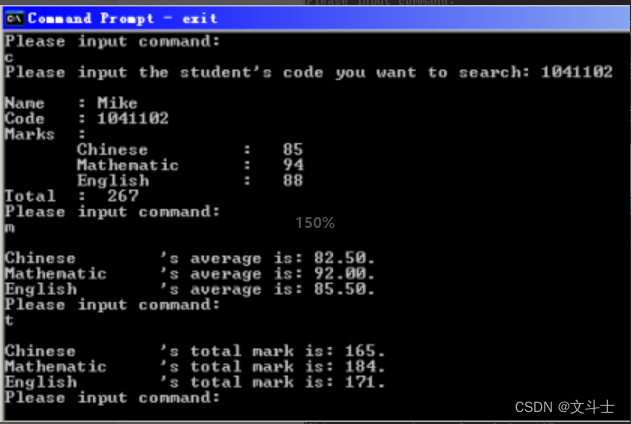
C语言例程:学生成绩管理程序
学生成绩管理程序 实例说明 编制一个统计存储在文件中的学生考试分数的管理程序。设学生成绩以一个学生一条记录的 形式存储在文件中,每个学生记录包含的信息有姓名、学号和各门功课的成绩。要求编制具有以 下几项功能的程序:求出各门课程的总分&#…...

完美日记母公司再度携手中国妇基会,以“创美人生”助力女性成长
撰稿 | 多客 来源 | 贝多财经 当春时节,梦想花开。和煦的三月暖阳,唤醒的不止是满城春意,更有逸仙电商“创美人生”公益项目播撒的一份希望。 3月8日“国际妇女节”当日,为积极响应我国促进共同富裕的政策倡导,助力相…...
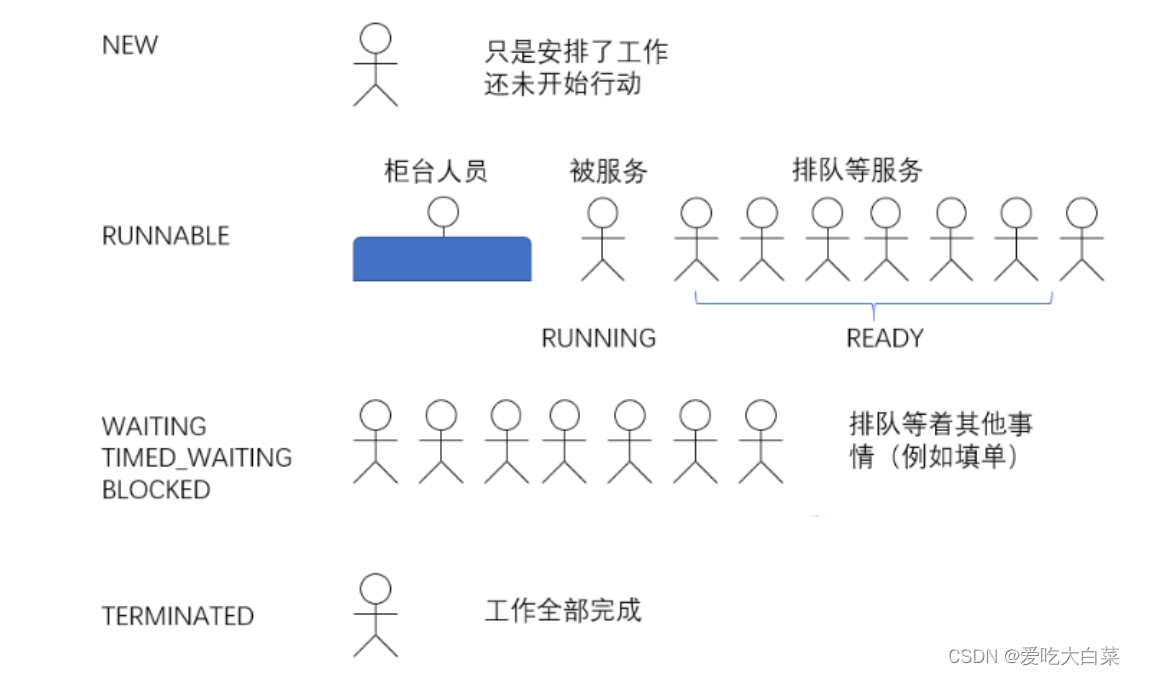
【JaveEE】线程的创建及常见方法解析(Tread类)
目录 1.Tread类介绍 2线程的构造方法——创建线程 1.继承Thread类,重写run()方法 2.使用Runnbable接口创建线程 3.继承 Thread, 重写 run, 使用匿名内部类 4.实现 Runnable, 重写 run, 使用匿名内部类 5.使用 lambda 表达式(重点掌握)…...

Linux的诞生过程
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。座右铭:海不辞水,故能成其大;山不辞石,故能成其高。个人主页:小李会科技的…...
面部表情识别1:表情识别数据集(含下载链接)
面部表情识别1:表情识别数据集(含下载链接) 目录 面部表情识别1:表情识别数据集(含下载链接) 1.前言 2.表情识别数据集介绍 1.JAFFE数据集 2.KDEF(Karolinska Directed Emotional Faces)数据集 3.GENKI数据集 4.RaFD数据集…...

CSS实现文字凹凸效果
使用两个div分别用来实现凹凸效果;text-shadow语法 text-shadow: h-shadow v-shadow blur color; h-shadow:必需。水平阴影的位置。允许负值。 v-shadow :必需。垂直阴影的位置。允许负值。 blur:可选,模糊的距离。 co…...

嵌入式常使用的库函数
自己创建简单的mcu中常用的库函数 文章目录自己创建简单的mcu中常用的库函数1. 自己编写库函数的意义2. 计算字符串长度.以\0作为结束符3. 复制字符串4. 字符串比较5. 将整数转换为ASCII数组6. 将ASCII码字符串转换成整数7. 将字节数组转换为16位整数8.计算CRC,用于Modbus协议9…...
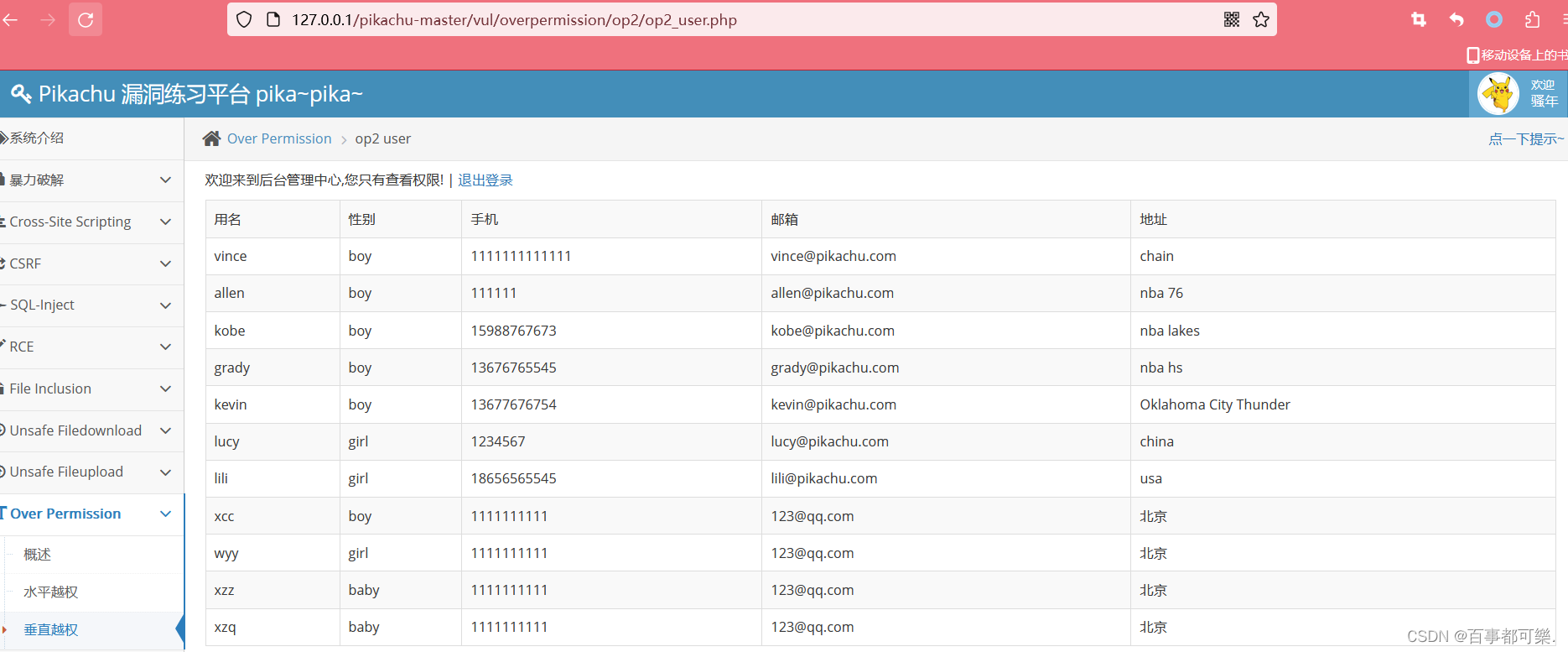
【业务安全-02】业务逻辑漏洞之越权操作
越权越权即越权查看被人的信息,又分为水平越权和垂直越权,但是两者的本质都是一样的,只是越权的身份权限不一样而已水平越权:相同级别的用户,如用户A访问用户B垂直越权:普通用户到管理员,普通用…...
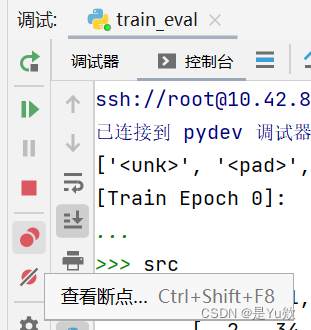
完全小白的pycharm深度学习调试+for循环断点条件设置
完全小白的pycharm深度学习调试for循环断点条件设置写在最前面基础方法pycharm断点调试控制台输入代码中循环的debug方法pycharm中图标的介绍常见的BugDebug经验1. 检查激活函数的输入值2. 检查梯度3. 消融实验4. 使用最短的时间5. 静下心来写在最前面 之前把seq2seqattention…...

直方图及其应用
直方图定义直方图是一种描述数据的分布通过将连续变量划分成一系列区间,统计区间频率,并用来表示,以表征其统计特征在图像处理中,直方图可以用来表示图像中像素值的分布状况,描述不同灰度级的像素在图像中的占比直方图…...
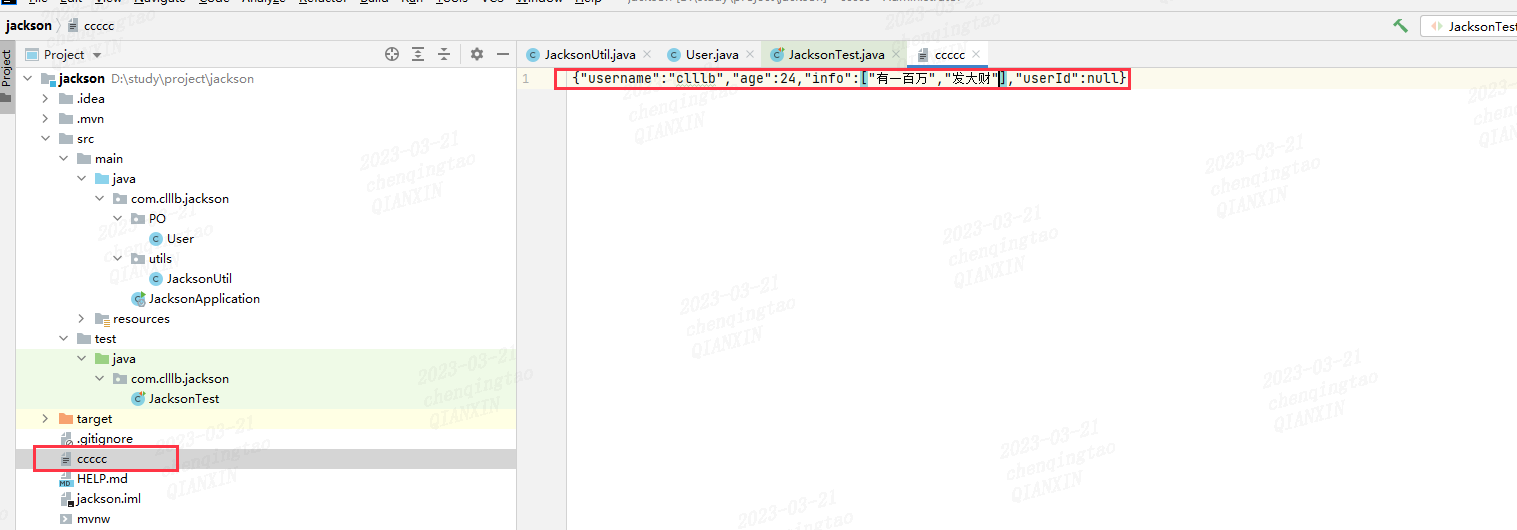
《SpringBoot篇》26.SpringBoot整合Jackson超详细教程(附Jackson工具类)
陈老老老板🦸👨💻本文专栏:SpringBoot篇(主要讲一些与springboot整合相关的内容)👨💻本文简述:本文讲一下Jackson常见用法,超级详细。👨&am…...
Redis 如何实现库存扣减操作和防止被超卖?
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
Ubuntu查看系统版本)
(Linux)Ubuntu查看系统版本
uname -a : 查看操作系统的发行版号和操作系统版本 Command: uname -aResult: Linux SERVER 5.19.0-35-generic #36-Ubuntu SMP PREEMPT_DYNAMIC Fri Feb 3 18:36:56 UTC 2023 x86_64 x86_64 x86_64 GNU/Linux uname -v : 查看版本号 Command: uname -vResult: #36-Ubuntu …...
)
VxWorkds 内存管理(3)
虚拟内存管理 对于带MMU的目标板,VxWorks提供虚拟内存的支持,VxWorks提供了两种虚拟内存管理单元(MMU)的支持: 基本MMU和VxVMI 基本MMU邦定于VxWorks中,可以通过config.h中宏定义INCLUDE MMU BASIC或Tornado工程配置中包含基本MMU组件 VxV…...

单元测试、反射、注解、动态代理
🏡个人主页 : 守夜人st 🚀系列专栏:Java …持续更新中敬请关注… 🙉博主简介:软件工程专业,在校学生,写博客是为了总结回顾一些所学知识点 目录单元测试、反射、注解、动态代理单元测…...

【数据结构】夯实基础|线性表刷题01
作者:努力学习的大一在校计算机专业学生,热爱学习和创作。目前在学习和分享:算法、数据结构、Java等相关知识。博主主页: 是瑶瑶子啦所属专栏: 【数据结构|刷题专栏】:该专栏专注于数据结构知识,持续更新&a…...
Java怎么实现几十万条数据插入(30万条数据插入MySQL仅需13秒)
本文主要讲述通过MyBatis、JDBC等做大数据量数据插入的案例和结果。 30万条数据插入插入数据库验证实体类、mapper和配置文件定义User实体mapper接口mapper.xml文件jdbc.propertiessqlMapConfig.xml不分批次直接梭哈循环逐条插入MyBatis实现插入30万条数据JDBC实现插入30万条数…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
