相关性检验
文章目录
- Pearson相关系数
- Spearman等级相关系数
- Cochran's Q检验
- Kappa一致性系数
- Kendall相关系数
- 实例分析
- 总结
在数据分析的广阔天地中,相关性检验是探索变量间关系的一把钥匙。本文将带领大家了解几种常用的相关性检验方法:Pearson、Spearman、Cochran’s Q、Kappa和Kendall。我们将深入每种方法的计算公式,并以几个实例,展示如何使用这些方法来计算相关性。
Pearson相关系数
Pearson相关系数是衡量两个连续变量线性相关程度的指标。其值介于-1到1之间,公式如下:
r Pearson = ∑ ( X i − X ˉ ) ( Y i − Y ˉ ) ∑ ( X i − X ˉ ) 2 ∑ ( Y i − Y ˉ ) 2 r_{\text{Pearson}} = \frac{\sum (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum (X_i - \bar{X})^2}\sqrt{\sum (Y_i - \bar{Y})^2}} rPearson=∑(Xi−Xˉ)2∑(Yi−Yˉ)2∑(Xi−Xˉ)(Yi−Yˉ)
其中, X i X_i Xi 和 Y i Y_i Yi 是观测值, X ˉ \bar{X} Xˉ 和 Y ˉ \bar{Y} Yˉ 是它们的均值。
Spearman等级相关系数
Spearman等级相关系数适用于非参数数据,衡量两个变量的单调关系。计算公式如下:
r Spearman = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) r_{\text{Spearman}} = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} rSpearman=1−n(n2−1)6∑di2
d i d_i di 是排名差, n n n 是观测值数量。
Cochran’s Q检验
Cochran’s Q检验用于三个或更多个相关比例的差异性检验。其公式为:
Q = k − 1 2 + 1 2 × n ∑ ( p i − p overall ) 2 Q = k - \frac{1}{2} + \frac{1}{2 \times n} \sum (p_i - p_{\text{overall}})^2 Q=k−21+2×n1∑(pi−poverall)2
k k k 是比例的数量, p i p_i pi 是第 i i i 个比例, p overall p_{\text{overall}} poverall 是所有比例的平均值。
Kappa一致性系数
Kappa一致性系数用于衡量两个评估者在分类数据上的一致性。其计算公式如下:
κ = p o − p e 1 − p e \kappa = \frac{p_o - p_e}{1 - p_e} κ=1−pepo−pe
p o p_o po 是观察到的一致性比例, p e p_e pe 是偶然一致性的比例。
Kendall相关系数
Kendran的tau-b相关系数是衡量两个变量相关性的非参数方法。其计算公式如下:
τ b = 2 ( number of concordant pairs ) − 2 ( number of discordant pairs ) n ( n − 1 ) \tau_b = \frac{2(\text{number of concordant pairs}) - 2(\text{number of discordant pairs})}{n(n-1)} τb=n(n−1)2(number of concordant pairs)−2(number of discordant pairs)
实例分析
实例数据
| 学生 | 测试1 | 测试2 |
|---|---|---|
| A | 78 | 82 |
| B | 85 | 80 |
| C | 90 | 88 |
| D | 60 | 65 |
| E | 70 | 75 |
Pearson相关系数
X ˉ = 78 + 85 + 90 + 60 + 70 5 = 76 \bar{X} = \frac{78 + 85 + 90 + 60 + 70}{5} = 76 Xˉ=578+85+90+60+70=76
Y ˉ = 82 + 80 + 88 + 65 + 75 5 = 79 \bar{Y} = \frac{82 + 80 + 88 + 65 + 75}{5} = 79 Yˉ=582+80+88+65+75=79
r Pearson = ( 78 − 76 ) ( 82 − 79 ) + . . . + ( 70 − 76 ) ( 75 − 79 ) ( ( 78 − 76 ) 2 + . . . + ( 70 − 76 ) 2 ) ( ( 82 − 79 ) 2 + . . . + ( 75 − 79 ) 2 ) r_{\text{Pearson}} = \frac{(78-76)(82-79) + ... + (70-76)(75-79)}{\sqrt{((78-76)^2 + ... + (70-76)^2)((82-79)^2 + ... + (75-79)^2)}} rPearson=((78−76)2+...+(70−76)2)((82−79)2+...+(75−79)2)(78−76)(82−79)+...+(70−76)(75−79)
r Pearson = 0.967 r_{\text{Pearson}} = 0.967 rPearson=0.967(四舍五入到小数点后三位)
Spearman等级相关系数
等级分配:
- 测试1: A(3), B(5), C(5), D(1), E(2)
- 测试2: A(4), B(3), C(5), D(1), E(3)
计算 d i d_i di并应用公式,我们得到:
r Spearman = 1 r_{\text{Spearman}} = 1 rSpearman=1(因为排名完全一致)
Kendall相关系数
计算一致对和不一致对的数量:
- 一致对:(A,B), (B,C), (C,E) - 3对
- 不一致对:(A,C), (A,D), (A,E), (B,D), (B,E), (D,E) - 6对
τ b = 2 ( 3 ) − 2 ( 6 ) 5 ( 5 − 1 ) = − 4 8 = − 0.5 \tau_b = \frac{2(3) - 2(6)}{5(5-1)} = -\frac{4}{8} = -0.5 τb=5(5−1)2(3)−2(6)=−84=−0.5(负相关)
Python代码
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import pearsonr, spearmanr# 定义数据
data = {'测试1': [78, 85, 90, 60, 70],'测试2': [82, 80, 88, 65, 75]
}# 创建DataFrame
df = pd.DataFrame(data)# 计算Pearson和Spearman相关系数
pearson_corr, _ = pearsonr(df['测试1'], df['测试2'])
spearman_corr, _ = spearmanr(df['测试1'], df['测试2'])# 创建相关性矩阵
corr_matrix = {'测试1': [pearson_corr, spearman_corr],'测试2': [spearman_corr, 1] # 假设测试1和测试2完全相关
}# 创建DataFrame
corr_df = pd.DataFrame(corr_matrix, index=['测试1', '测试2'])# 绘制热力图
sns.heatmap(corr_df, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('相关性热力图')
plt.show()
总结
通过上述分析,我们可以看到不同相关性检验方法如何揭示变量间的关系。每种方法都有其特定的应用场景和优势。选择合适的方法来分析你的数据,可以更准确地理解变量间的相互作用。
相关文章:

相关性检验
文章目录 Pearson相关系数Spearman等级相关系数Cochrans Q检验Kappa一致性系数Kendall相关系数实例分析总结 在数据分析的广阔天地中,相关性检验是探索变量间关系的一把钥匙。本文将带领大家了解几种常用的相关性检验方法:Pearson、Spearman、Cochran’s…...

【python】Django运行报错分析:ImproperlyConfigured 错误解决办法
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

AS01/AS11 创建固资和子资产
AS01:创建资产卡片 定义该资产的折旧费用,应该归结到哪个成本中心。 如果一台设备停止使用,可以勾选。停止折旧。 该界面维护折旧码和折旧的时间。 维护完之后点击保存。 系统生成一个资产卡片号。 AS02-修改资产卡片号 更改不同时间段&…...

vue3数字动画插件countup.js
countup.js 是一个轻量级的 JavaScript 库,允许你为网站上显示统计数据或计数器时平滑地动画化数字。CountUp 类被用来创建计数器实例,可以平滑地从一个数值变化到另一个数值。 只是用户视觉更好一些。 1、安装插件 npm i countup.js2、个人是封装了组件…...

aspeed2600 GPIO分析与适配ipmitool power status, ipmitool power on/off
1.说明 本节以x86-power-control/src/power_control.cpp为基础,分析整个GPIO的调用流程,实现简单的ipmitool power on/off,ipmitool power status的管理。 1.资源:x86-power-control:https://github.com/openbmc/x86-power-control2.相关文件: meta-ph…...

在C#中配置ini文件以及封装ini类
在C#中使用 DllImport 属性从 kernel32.dll 导入函数来写入和读取Windows的INI文件,你可以使用 WritePrivateProfileString 来写入数据,使用 GetPrivateProfileString 来读取数据。 以下是如何使用这些函数的示例: 写入INI文件 using Syst…...

使用git上传代码到github
1、设置用户名及邮箱 git config user.name"你的用户名"git config user.email"xxxxx.com" 2、查看配置 git config -l 3、生成秘钥 ssh-keygen -t rsa 根据上图中红框标出的id_rsa.pub地址,找到它,使用txt文件打开,复…...

滚珠花键:新能源汽车传动系统的核心动力传递者
在日常生活中,汽车已经成为了必不可少的交通工具,尤其是新能源汽车。而滚珠花键作为传动系统中的重要组成部分,在传动系统方面的作用不容忽视。 随着科技的不断发展,汽车行业也在不断进步,滚珠花键作为高精度的机械传动…...

LeetCode 149, 347, 31
文章目录 149. 直线上最多的点数题目链接标签思路总体思路如何判断 一个点 在 由两点确定的直线 上 代码 347. 前 K 个高频元素题目链接标签思路代码 31. 下一个排列题目链接标签思路代码 149. 直线上最多的点数 题目链接 149. 直线上最多的点数 标签 几何 数组 哈希表 数学…...
)
操作系统(信号处理)
一、信号介绍 什么是中断: 当进程接收到消息后中止当前正在执行的任务,转而执行其它任务,等待其它任务执行完毕后再返回继续执行。这种执行模式称为中断,分为硬件中断和软件中断两种 什么是信号: 信号是UNIX、类UNI…...
[MRCTF2020]Ezpop
[MRCTF2020]Ezpop 题目是pop,考的其实就是pop链,可以自己先学学,啥也不会QAQ php反序列化之pop链_pop3.phpwelcome-CSDN博客 POP 面向属性编程(Property-Oriented Programing) 常用于上层语言构造特定调用链的方法,与二进制利用…...

24暑假算法刷题 | Day27 | 贪心算法 I | LeetCode 455. 分发饼干,376. 摆动序列,53. 最大子数组和
目录 455. 分发饼干题目描述题解 376. 摆动序列题目描述题解 53. 最大子数组和题目描述题解 455. 分发饼干 点此跳转题目链接 题目描述 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i&#x…...

Golang 的空接口有什么用?
空接口在 Go 语言中具有多种重要用途: 实现通用的数据结构 例如,可以创建一个包含空接口类型元素的切片或映射,从而能够存储不同类型的值。这在处理多种未知类型的数据时非常有用。比如,一个日志系统可能会将不同类型的日志消息&a…...

计算机毕业设计选题推荐-课程教学平台-Java/Python项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...
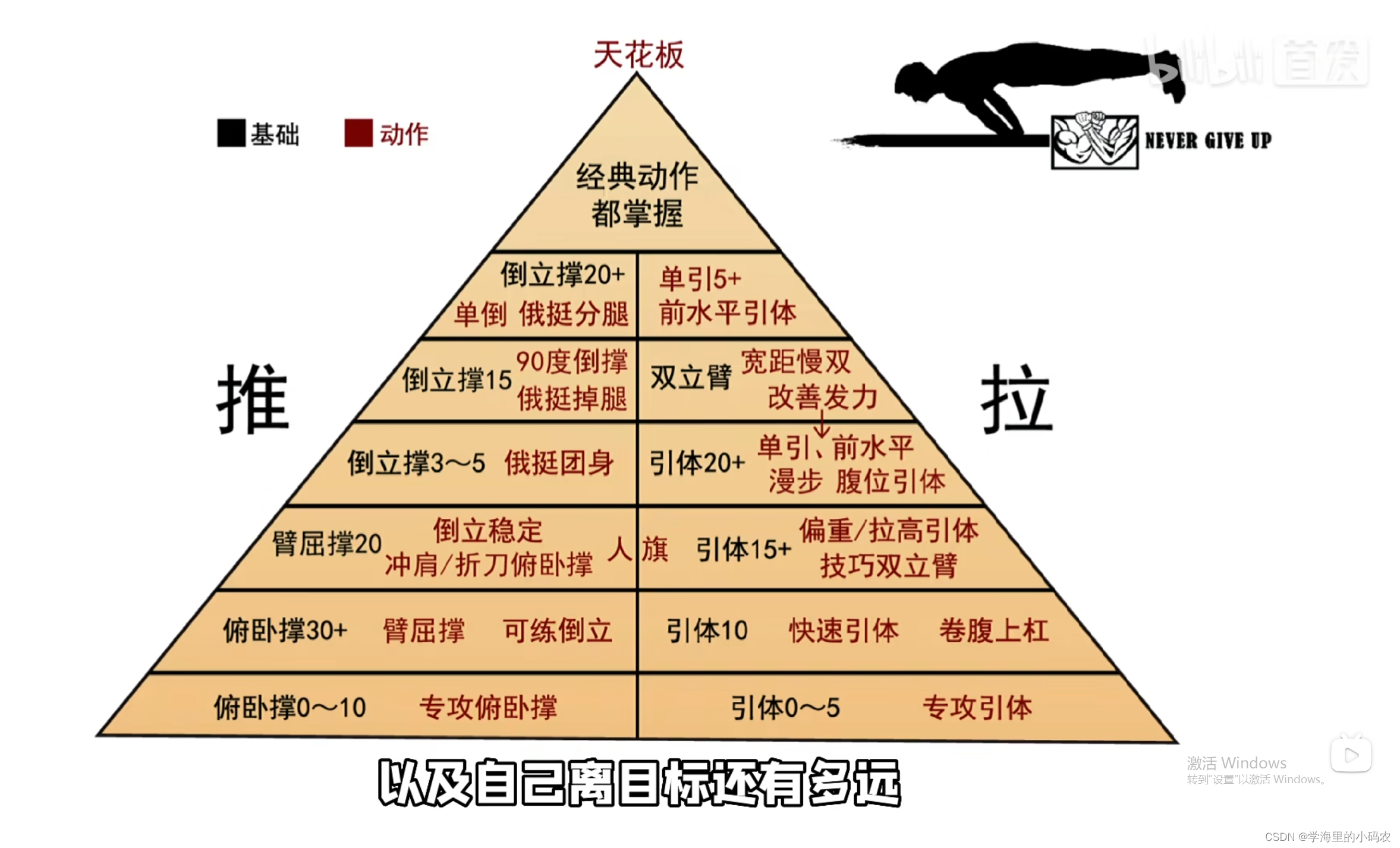
健身日记之倒立俯卧撑学习——起始日2024.6.4
文章目录 目录 前言上期预期 昔日计划 新目标计划 瓶颈突破尝试 参考视频及文章 前言 两个月过去了,已经有所突破了,但是比较预期还是有较大差距,忘记更新csdn了,平时抖音视频号记录的多一些。 上期预期 2024.6.4开始尝试突…...
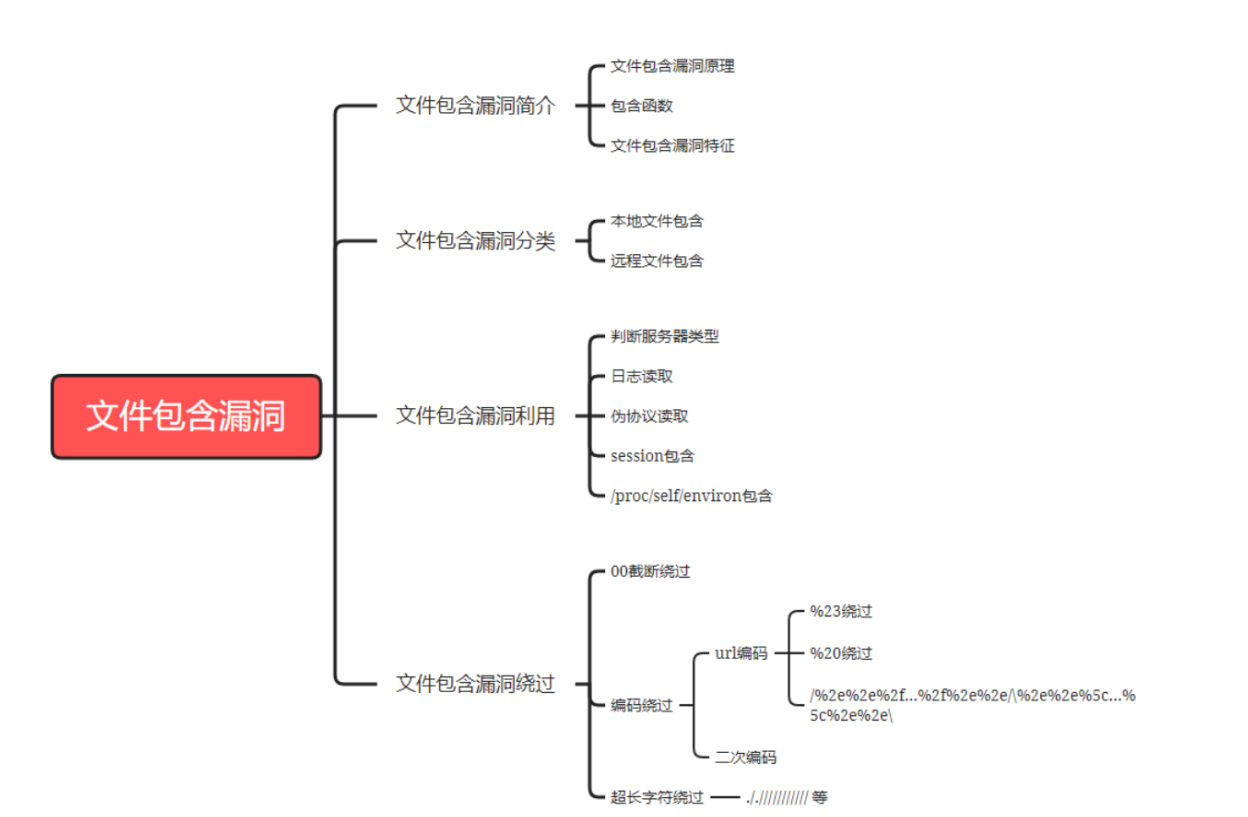
pikachu文件包含漏洞
一:漏洞基础 程序在引用文件的时,引用的文件名存在可控的情况,传入的文件名没有经过合理的校验或校验不严,从而操作了预想之外的文件,就有可能导致文件泄漏和恶意的代码注入; 文件包含漏洞概念 在PHP程序…...

09.FreeRTOS时间片调度与任务相关函数
文章目录 09. FreeRTOS时间片调度与任务相关函数1. FreeRTOS时间片调度2. 任务状态查询API函数3. 任务时间统计API函数 09. FreeRTOS时间片调度与任务相关函数 1. FreeRTOS时间片调度 时间片调度简介: 时间片调度实验流程: 核心代码: 开…...

git分支介绍
git branch 查看当前分支情况 可以看见当前只有一个分支叫main,也就是默认分支,可以理解为树的主干,git早期版本中默认分支叫master 命令行创建一个新分支 git branch [分支名]在创建之后,如果需要切换到新分支需要git switc…...

vm虚拟机下安装CentOS7系统
VMware16安装CentOS7 1.启动之前安装的VM 具体VMware安装过程 2.配置Linux(centos7)的镜像文件 选择安装镜像文件 4.开启虚拟机 开始读秒安装 选择安装过程中使用的语言,这里选择英文、键盘选择美式键盘。点击Continue 首先设置时间…...
python-报数(赛氪OJ)
[题目描述] 有 n 人围成一圈,顺序排号。 从第 1 个人开始报数(从 1 到 3 报数),凡是报到 3 的人退出圈子,问最后留下的是原来的第几号的那位。输入格式: 初始人数 n 。输出格式: 最后一人的初始…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
