LeetCode 149, 347, 31
文章目录
- 149. 直线上最多的点数
- 题目链接
- 标签
- 思路
- 总体思路
- 如何判断 一个点 在 由两点确定的直线 上
- 代码
- 347. 前 K 个高频元素
- 题目链接
- 标签
- 思路
- 代码
- 31. 下一个排列
- 题目链接
- 标签
- 思路
- 代码
149. 直线上最多的点数
题目链接
149. 直线上最多的点数
标签
几何 数组 哈希表 数学
思路
总体思路
本题是一道 数学题,可以采取 暴力 的方式:
- 先 枚举所有由两点连接而成的直线,即 枚举任意两个点 计算其所在直线。
- 然后再 枚举所有点,统计 每条直线上的点的数量 的最大值。
可以稍微对这种方式进行优化:
- 将第一步中的 枚举任意两个点 改为 枚举 任意点 和 其之后的所有点。防止 计算完点 A A A 和点 B B B 所在直线上的点的数量之后,再计算点 B B B 和点 A A A 所在直线上的点的数量 这样的重复计算。
- 将第二步中的 枚举所有点 改为 枚举 第一步枚举的两个点之后的 所有点。避免了重复计算。
如何判断 一个点 在 由两点确定的直线 上
接下来就需要考虑如何判断一个点 在 由两点确定的直线 上,其实并不难,既然已经枚举出两个点 P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) P_1(x_1, y_1), P_2(x_2, y_2) P1(x1,y1),P2(x2,y2),对于第三个点 P 3 ( x 3 , y 3 ) P_3(x_3, y_3) P3(x3,y3),只要 第一个点 和 第二个点 所确定直线的斜率 与 第二个点 和 第三个点 所确定直线的斜率 相同,则点 P 3 P_3 P3 在直线 P 1 P 2 P_1P_2 P1P2 上。斜率相同可以表示如下:
x 1 − x 2 y 1 − y 2 = x 2 − x 3 y 2 − y 3 \frac{x_1 - x_2}{y_1 - y_2} = \frac{x_2 - x_3}{y_2 - y_3} y1−y2x1−x2=y2−y3x2−x3
但是,在程序中无法使用 int, double 表示分数,如果强行使用,则会造成一定的精度损失,导致结果错误。所以考虑 将 除法 变成 乘法,斜率相同表示如下:
( y 2 − y 3 ) ( x 1 − x 2 ) = ( x 2 − x 3 ) ( y 1 − y 2 ) (y_2 - y_3) (x_1 - x_2) = (x_2 - x_3) (y_1 - y_2) (y2−y3)(x1−x2)=(x2−x3)(y1−y2)
确定第三个点是否在直线上时,需要多次使用 ( x 1 − x 2 ) (x_1 - x_2) (x1−x2) 和 ( y 1 − y 2 ) (y_1 - y_2) (y1−y2),所以用变量来记录它们: Δ x = ( x 1 − x 2 ) , Δ y = ( y 1 − y 2 ) \Delta x = (x_1 - x_2), \Delta y = (y_1 - y_2) Δx=(x1−x2),Δy=(y1−y2),斜率相同表示如下:
( y 2 − y 3 ) Δ x = ( x 2 − x 3 ) Δ y (y_2 - y_3) \Delta x = (x_2 - x_3) \Delta y (y2−y3)Δx=(x2−x3)Δy
代码
class Solution {public int maxPoints(int[][] points) {int n = points.length; // 获取数组中点的数量if (n <= 2) { // 如果点的数量小于等于 2return n; // 则直接返回点的数量即可}int res = 0; // 保存结果for (int i = 0; i < n; i++) {int[] p1 = points[i]; // 第一个点for (int j = i + 1; j < n; j++) {int[] p2 = points[j]; // 第二个点int deltaX = p1[0] - p2[0]; // p1 和 p2 的横坐标的差值int deltaY = p1[1] - p2[1]; // p1 和 p2 的纵坐标的差值// 统计有多少个点位于 p1 与 p2 所确定的直线上,初始值为 2 表示 p1 和 p2 位于这条直线上int cnt = 2;for (int k = j + 1; k < n; k++) {int[] p3 = points[k]; // 第三个点// 如果 p3 在 p1, p2 所确定的直线上,则点数加一if ((p3[1] - p2[1]) * deltaX == (p3[0] - p2[0]) * deltaY) {cnt++;}}res = Math.max(res, cnt); // 更新最大值}}return res;}
}
347. 前 K 个高频元素
题目链接
347. 前 K 个高频元素
标签
数组 哈希表 分治 桶排序 计数 快速选择 排序 堆(优先队列)
思路
本题可以使用 优先队列,和 LeetCode 215. 数组中的第K个最大元素 很相似,都使用 小顶堆 来存放数组中优先级前 K 高的元素,不过本题中元素的优先级不是元素的值,而是元素的出现次数。
本题直接使用 Java 中的 PriorityQueue 优先队列,(用一个长度为 2 的数组作为类型参数)保存元素的值和出现次数。此外,需要在构造器中传入一个 比较器,定义优先队列内部存储的数据如何进行比较。
代码
class Solution {public int[] topKFrequent(int[] nums, int k) {// 统计每个元素出现的次数,key 为元素的值,value 为元素出现的次数Map<Integer, Integer> cnt = new HashMap<>(nums.length);for (int num : nums) {cnt.put(num, cnt.getOrDefault(num, 0) + 1);}// 小顶堆,元素出现的次数越少,越靠近顶部。存放着数组中频率前 k 高的元素// 在 int[] 中存放了 2 个值,第一个值表示 元素的值,第二个值表示 元素出现的次数PriorityQueue<int[]> pq = new PriorityQueue<>((p1, p2) -> p1[1] - p2[1]);for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) { // 构建小顶堆int num = entry.getKey(), count = entry.getValue();if (pq.size() < k) { // 如果小顶堆中的元素少于 k 个pq.offer(new int[]{num, count}); // 则给其中添加元素} else if (count > pq.peek()[1]) {// 此时元素个数等于 k 个,如果 当前元素的出现次数 大于 堆顶元素的出现次数pq.poll(); // 则移除堆顶元素pq.offer(new int[]{num, count}); // 将当前元素放入堆中}}// 构造结果数组并返回int[] res = new int[k];for (int i = 0; i < k; i++) {res[i] = pq.poll()[0];}return res;}
}
31. 下一个排列
题目链接
31. 下一个排列
标签
数组 双指针
思路
本题是 纯技巧题,只要会这个技巧便能解决本题,如果不会,最好将其 背 下来。这个技巧分为如下三步:
- 寻找:
- 在数组中,从右向左寻找 小于它右边的数 的数,将其称为 逆数。例如
[1, 2, 5, 4, 6, 3]中的4。- 如果在数组中找到了 逆数,那么从 最后一个数 到 逆数 的下一个数,寻找一个 比 逆数 大 的数,将其称为 大数。例如
[1, 2, 5, 4, 6, 3]中的6。- 交换:如果能找到 大数,则交换这两个数。
- 反转:
- 如果在数组中找到了 逆数,则将 逆数 的下一个数 到 最后一个数 的范围内的所有数进行反转操作。
- 如果在数组中没有找到 逆数,则将整个数组都进行反转操作。
如果很难理解这个技巧,不妨来看看这个例子,至少知道它可以使用:
对于数组 [1, 2, 5, 4, 6, 3]
-----------------------------------
寻找逆数和比逆数大的数,分别用 i, j 指向:
[1, 2, 5, 4, 6, 3]^ ^i j
-----------------------------------
交换 i, j 指向的数:
[1, 2, 5, 6, 4, 3]^i
-----------------------------------
反转 i + 1 之后的部分:
[1, 2, 5, 6, 3, 4]
代码
class Solution {public void nextPermutation(int[] nums) {final int n = nums.length;// 从右往左扫描,直到找到一个 比它右边的数小的 数int i = n - 2;while (i >= 0 && nums[i] >= nums[i + 1]) {i--;}// 如果在数组中找到了逆数if (i >= 0) {// 则 在 索引为 i + 1 的数 到 最后一个数 的范围内,寻找一个比逆数大的数int j = n - 1;while (j > i && nums[i] >= nums[j]) {j--;}// 交换它们swap(nums, i, j);}// 反转 i + 1 之后的部分reverse(nums, i + 1);}// 交换 nums 中索引 i, j 指向的元素private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}// 从 start 开始反转 nums 数组private void reverse(int[] nums, int start) {int left = start, right = nums.length - 1;while (left < right) {swap(nums, left, right);left++;right--;}}
}
相关文章:

LeetCode 149, 347, 31
文章目录 149. 直线上最多的点数题目链接标签思路总体思路如何判断 一个点 在 由两点确定的直线 上 代码 347. 前 K 个高频元素题目链接标签思路代码 31. 下一个排列题目链接标签思路代码 149. 直线上最多的点数 题目链接 149. 直线上最多的点数 标签 几何 数组 哈希表 数学…...
)
操作系统(信号处理)
一、信号介绍 什么是中断: 当进程接收到消息后中止当前正在执行的任务,转而执行其它任务,等待其它任务执行完毕后再返回继续执行。这种执行模式称为中断,分为硬件中断和软件中断两种 什么是信号: 信号是UNIX、类UNI…...
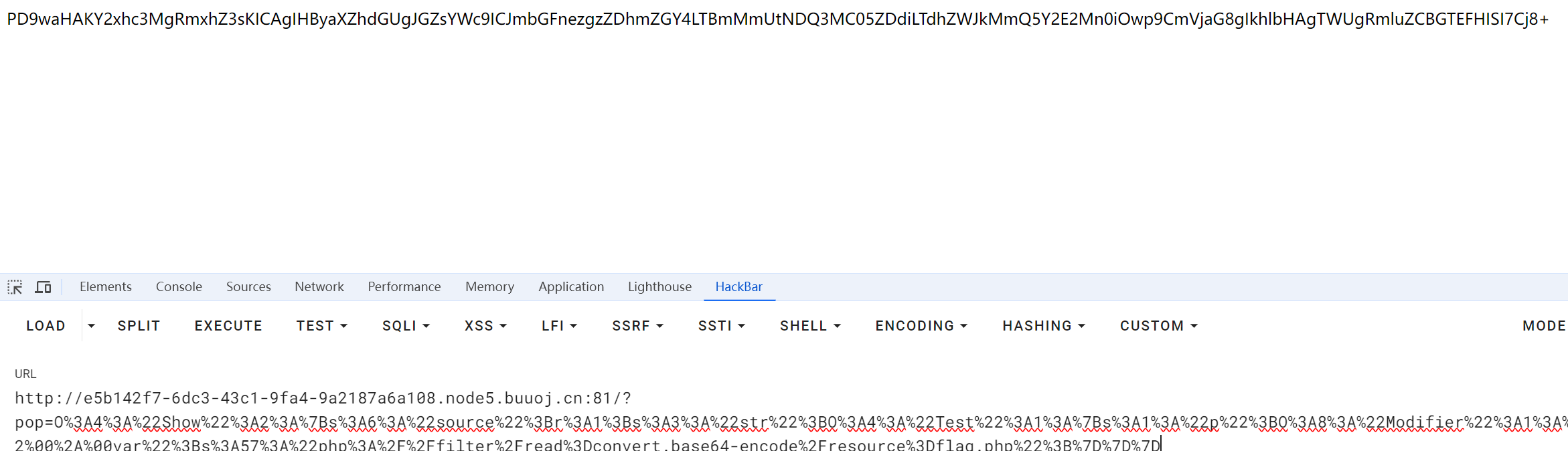
[MRCTF2020]Ezpop
[MRCTF2020]Ezpop 题目是pop,考的其实就是pop链,可以自己先学学,啥也不会QAQ php反序列化之pop链_pop3.phpwelcome-CSDN博客 POP 面向属性编程(Property-Oriented Programing) 常用于上层语言构造特定调用链的方法,与二进制利用…...

24暑假算法刷题 | Day27 | 贪心算法 I | LeetCode 455. 分发饼干,376. 摆动序列,53. 最大子数组和
目录 455. 分发饼干题目描述题解 376. 摆动序列题目描述题解 53. 最大子数组和题目描述题解 455. 分发饼干 点此跳转题目链接 题目描述 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i&#x…...

Golang 的空接口有什么用?
空接口在 Go 语言中具有多种重要用途: 实现通用的数据结构 例如,可以创建一个包含空接口类型元素的切片或映射,从而能够存储不同类型的值。这在处理多种未知类型的数据时非常有用。比如,一个日志系统可能会将不同类型的日志消息&a…...

计算机毕业设计选题推荐-课程教学平台-Java/Python项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...
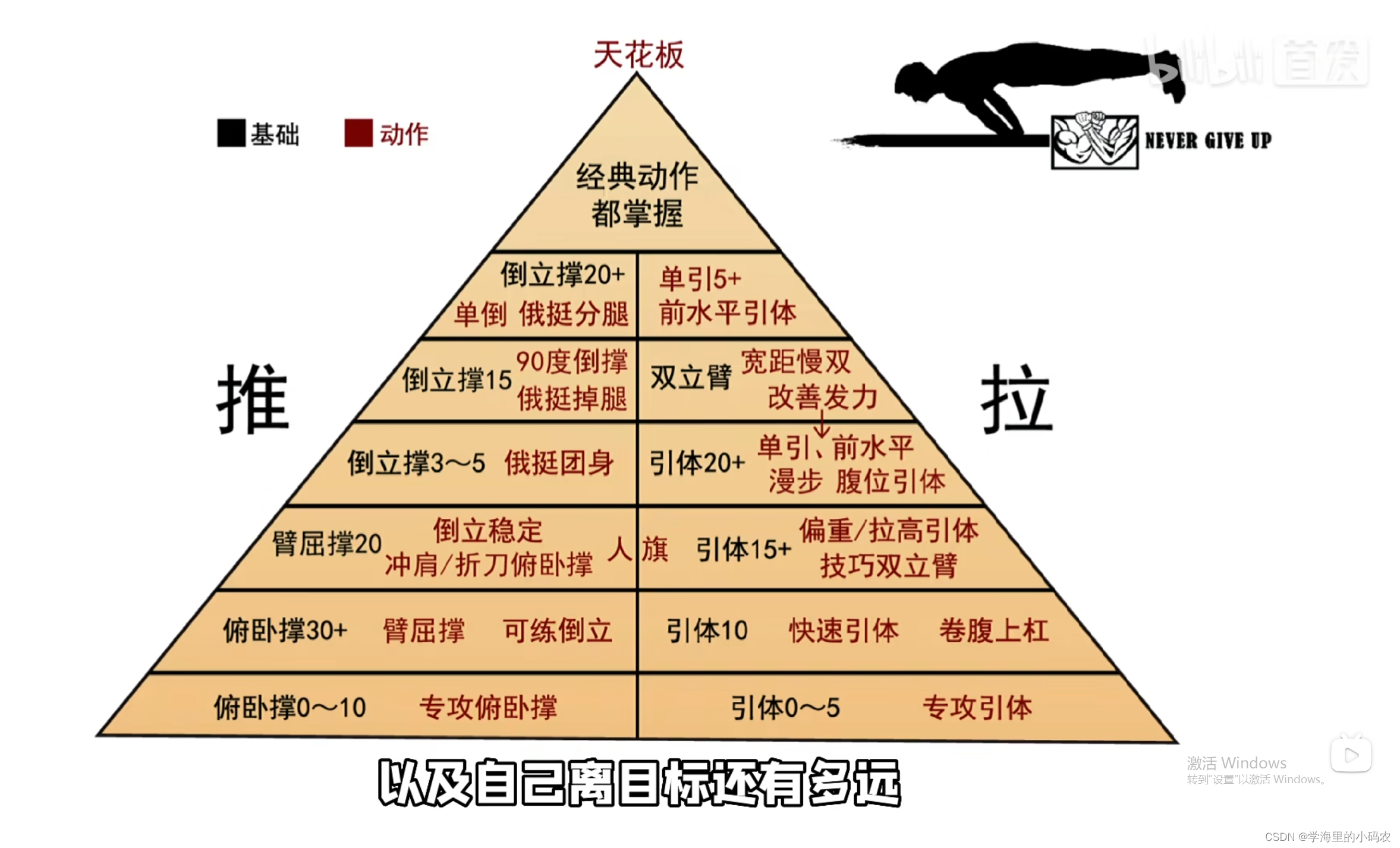
健身日记之倒立俯卧撑学习——起始日2024.6.4
文章目录 目录 前言上期预期 昔日计划 新目标计划 瓶颈突破尝试 参考视频及文章 前言 两个月过去了,已经有所突破了,但是比较预期还是有较大差距,忘记更新csdn了,平时抖音视频号记录的多一些。 上期预期 2024.6.4开始尝试突…...
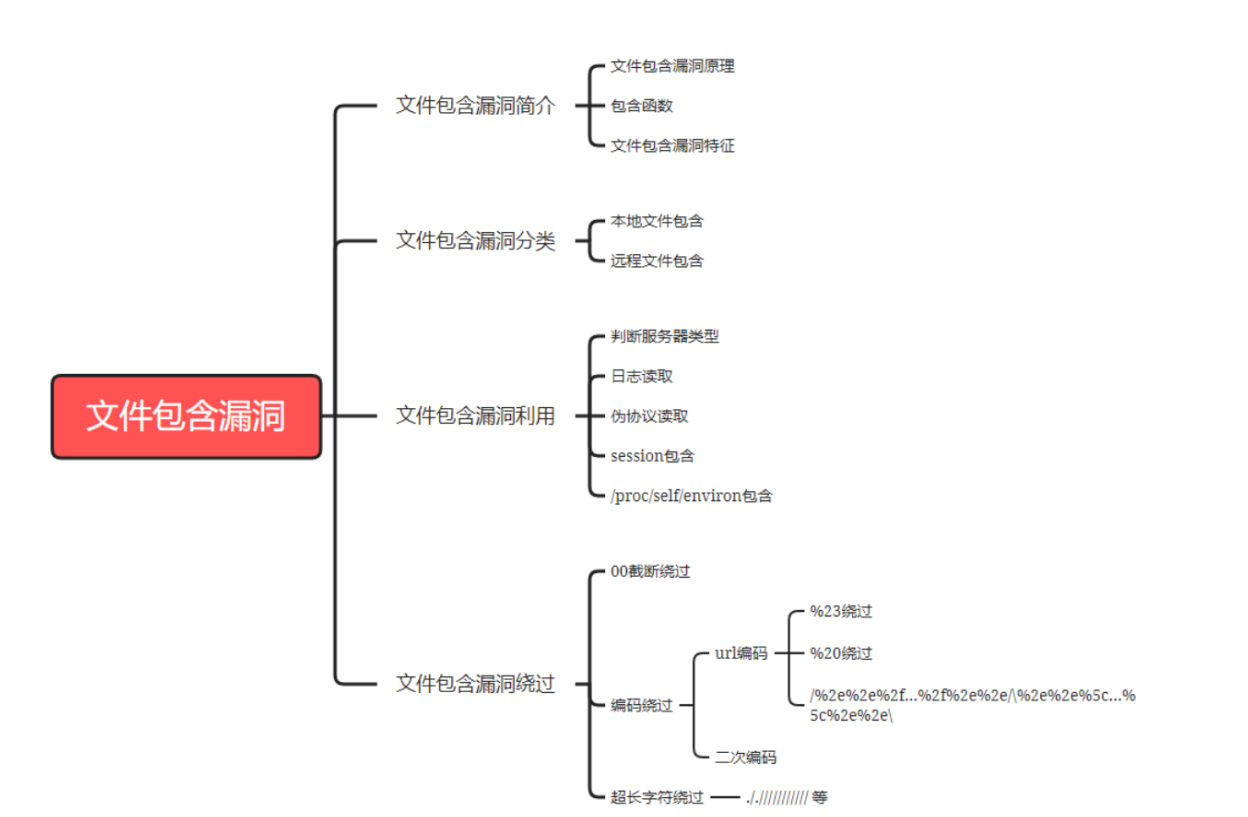
pikachu文件包含漏洞
一:漏洞基础 程序在引用文件的时,引用的文件名存在可控的情况,传入的文件名没有经过合理的校验或校验不严,从而操作了预想之外的文件,就有可能导致文件泄漏和恶意的代码注入; 文件包含漏洞概念 在PHP程序…...

09.FreeRTOS时间片调度与任务相关函数
文章目录 09. FreeRTOS时间片调度与任务相关函数1. FreeRTOS时间片调度2. 任务状态查询API函数3. 任务时间统计API函数 09. FreeRTOS时间片调度与任务相关函数 1. FreeRTOS时间片调度 时间片调度简介: 时间片调度实验流程: 核心代码: 开…...

git分支介绍
git branch 查看当前分支情况 可以看见当前只有一个分支叫main,也就是默认分支,可以理解为树的主干,git早期版本中默认分支叫master 命令行创建一个新分支 git branch [分支名]在创建之后,如果需要切换到新分支需要git switc…...

vm虚拟机下安装CentOS7系统
VMware16安装CentOS7 1.启动之前安装的VM 具体VMware安装过程 2.配置Linux(centos7)的镜像文件 选择安装镜像文件 4.开启虚拟机 开始读秒安装 选择安装过程中使用的语言,这里选择英文、键盘选择美式键盘。点击Continue 首先设置时间…...
python-报数(赛氪OJ)
[题目描述] 有 n 人围成一圈,顺序排号。 从第 1 个人开始报数(从 1 到 3 报数),凡是报到 3 的人退出圈子,问最后留下的是原来的第几号的那位。输入格式: 初始人数 n 。输出格式: 最后一人的初始…...

灵办AI:智能插件,办公与编程的得力助手
目录 引言一、灵办AI:智能化的办公伙伴二、编程能力:🔥代码阅读,学习助手🔥1、代码解读2、代码续写3、代码优化 三、插件端对话功能:智能交互,流畅体验四、翻译功能:一键翻译&#x…...

食家巷小程序:传统面点与平凉特产的美味盛宴
在美食的世界里,总有一些角落等待着我们去探索,而食家巷小程序就是这样一个为您开启美食宝藏的钥匙。 一、传统面点,传承千年的美味 食家巷小程序为您呈现了种类丰富的传统面点,每一款都蕴含着深厚的历史和文化底蕴。 平凉锅盔&…...

矢量文件坐标转换:2000坐标系转换为wgs84坐标系,具体代码实现
最近在处理矢量样本的时候,遇到一些shp文件的坐标系为2000坐标,需要统一地把非WGS84坐标系的矢量转换为WGS84坐标系。 本文记录一下如何进行2000坐标系转化为wgs84坐标系的过程。 在处理矢量数据转换的过程中,有几个关键步骤确保了数据的有效…...

MySQL-InnoDB引擎
目录 逻辑存储结构 架构 概述 内存结构 Buffer Pool(缓冲池) Change Buffer(更改缓冲区) Adaptive Hash Index(自适应hash索引) Log Buffer(日志缓冲区) 磁盘结构 System T…...

【Material-UI】复杂按钮 (Complex Button) 自定义详解
文章目录 一、ButtonBase 组件简介二、实例讲解:创建复杂的图片按钮1. 样式定义2. 核心组件构建3. 交互效果 三、高级自定义技巧1. 响应式设计2. 动态内容与动画 四、总结 在现代 Web 应用中,按钮不仅仅是一个点击交互元素,它们也承载着传递信…...
IT服务质量管理攻略(至简)
质量管理、风险管理和信息安全管理是IT服务监督管理的重要内容,三者之间相对独立。IT服务质量管理是通过制订质量方针、质量目标和质量计划,实施质量控制、质量保证和质量改进活动,确保IT服务满足服务级别协议的要求,最终获得用户…...

MySQL事务隔离级别、InnoDB使用MVCC+各种锁实现了RC和RR事务隔离级别、具体案例
事务隔离级别 脏读:一个事务读取到另一个未提交事务的更改。不可重复读:一个事务在两次读取同一数据时,发现数据被另一个已提交事务修改了。幻读:一个事务在读取过程中,因其他事务的插入而导致返回的行数不一致&#…...

你的Java项目还在等待吗?快来学会线程池,解放你的性能!
文章目录 你的Java项目还在等待吗?快来学会线程池,解放你的性能!1 什么是线程池?为什么需要它?2 线程池的参数有哪些?3 不同类型的线程池有哪些配置? 你的Java项目还在等待吗?快来学…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
