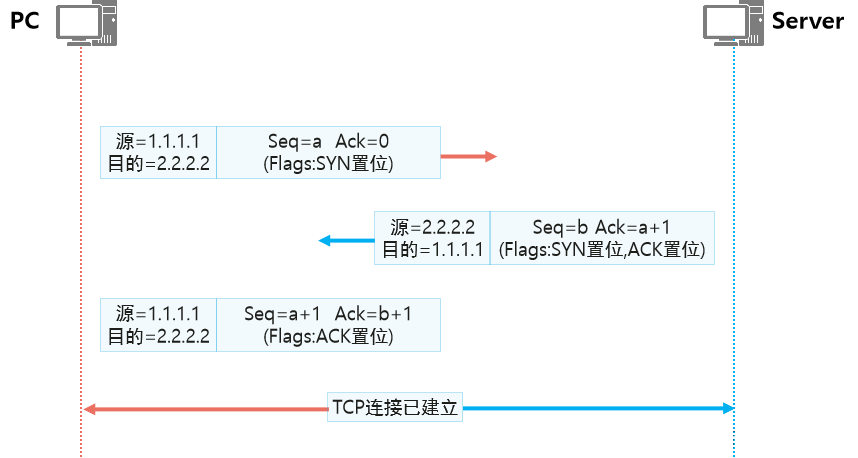
TCP三次握手/四次挥手
TCP三次握手
任何基于TCP的应用,在发送数据之前,都需要由TCP进行“三次握手”建立连接
示意图
第一次握手:客户端PC发送一个SYN位置1(SYN=1代表请求服务端建立连接)的TCP报文发送给要建立TCP连接的Server,此时Seq序列号值为a(随机值),由于没有收到Server发来的任何报文,所以Ack确认序列号为0
第二次握手:Server收到SYN标置位报文后,会对报文进行应答,发给PC的应答报文不仅有SYN置位(此时Seq的序列号值b为随机值),还会有ACK置位来说明已经收到PC发送的报文(因为PC1发来SYN置位消耗了一个序号为a的TCP数据,因此Server收到后,Ack的序列确认号要使用a+1来进行确认)。
发送的确认报文段包含以下字段:
SYN=1,同意建立新连接(SYN置位)
Seq=b, 服务端给返回确认的报文,加上自己的序列号
Ack_seq=a+1, 表示已经收到seq=a的报文段,并期望后续接收a+1序号的报文
ACK=1 确认收到请求报文(ACK置位)
第三次握手:客户端收到服务器的主动请求建立连接和确认报文时,客户端无需应答服务器的确认报文,但需要对服务器主动请求做应答,所以只是ACK置位,SYN不置位,Seq=a+1(Server期望的序列号值),Ack_seq=b+1(
TCP连接建立
(注意:ACK标志位和ACK确认序列号是两码事,不要混淆)
抓包分析

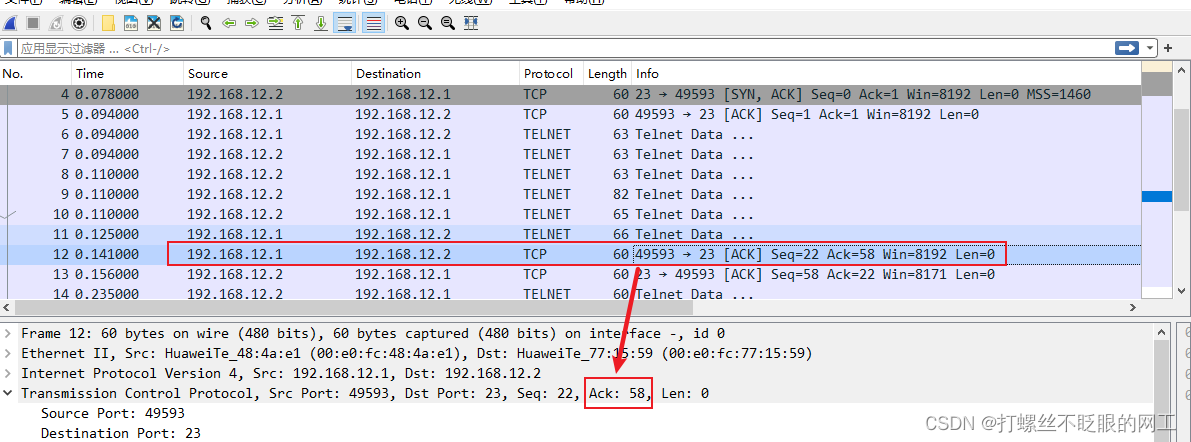
第一次握手,SYN置位,Seq=2755731984
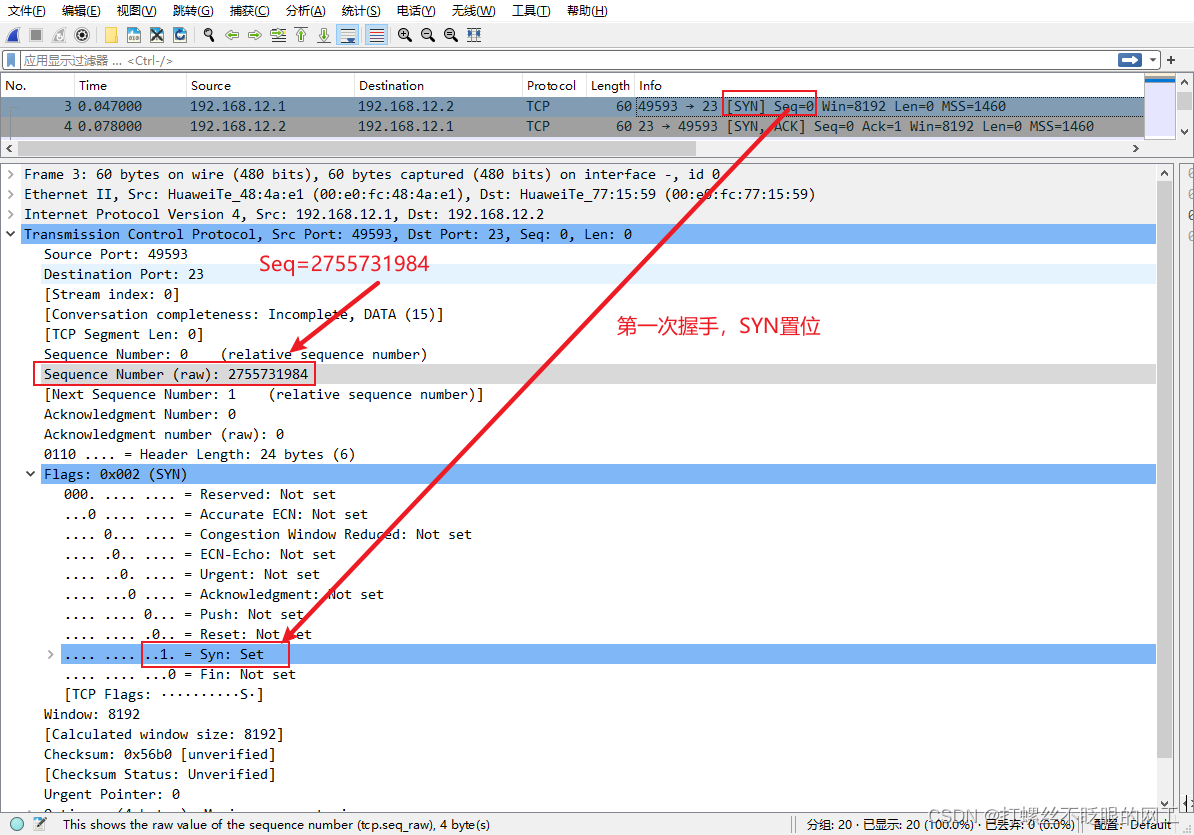
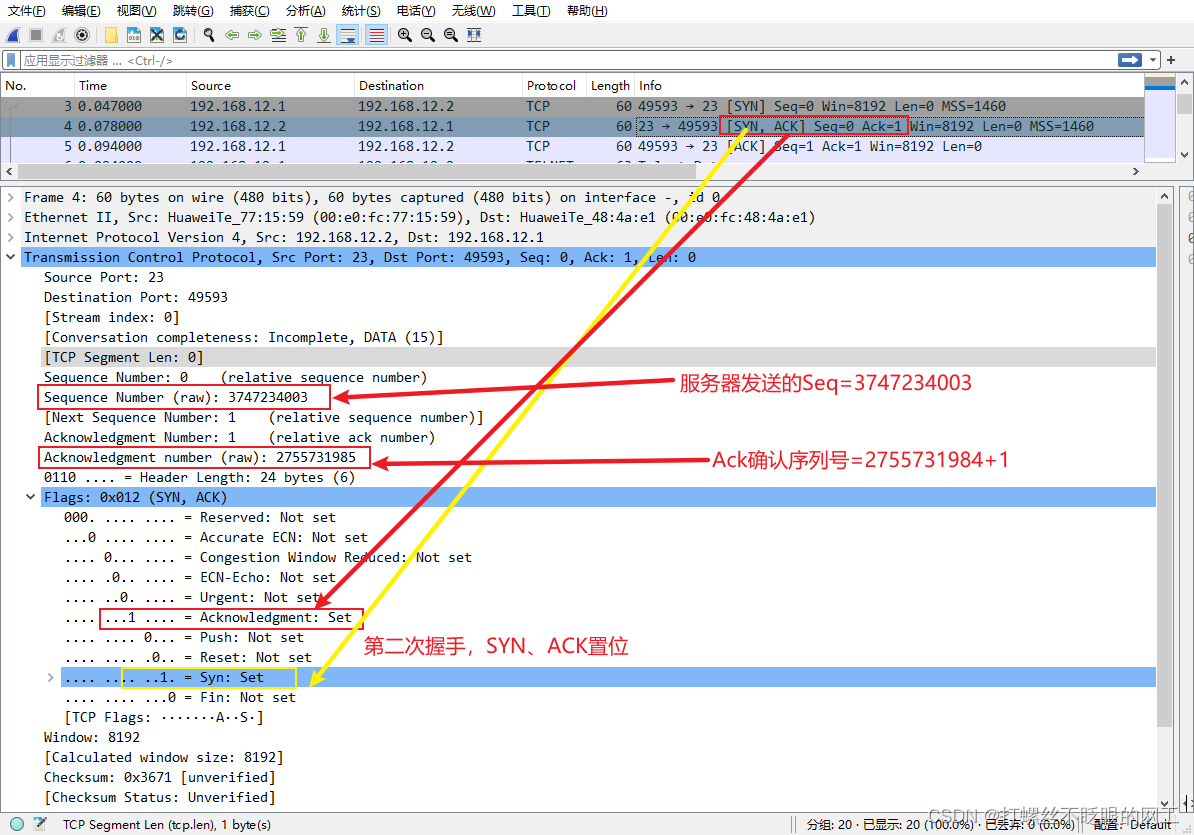
第二次握手,SYN、ACK置位,表示收到了客户端发来的请求,所以,Ack确认序列号=2755731984+1,同时发送自身的序列号Seq=3747234003
第三次握手,ACK置位,Ack的确认序列号=3747234003+1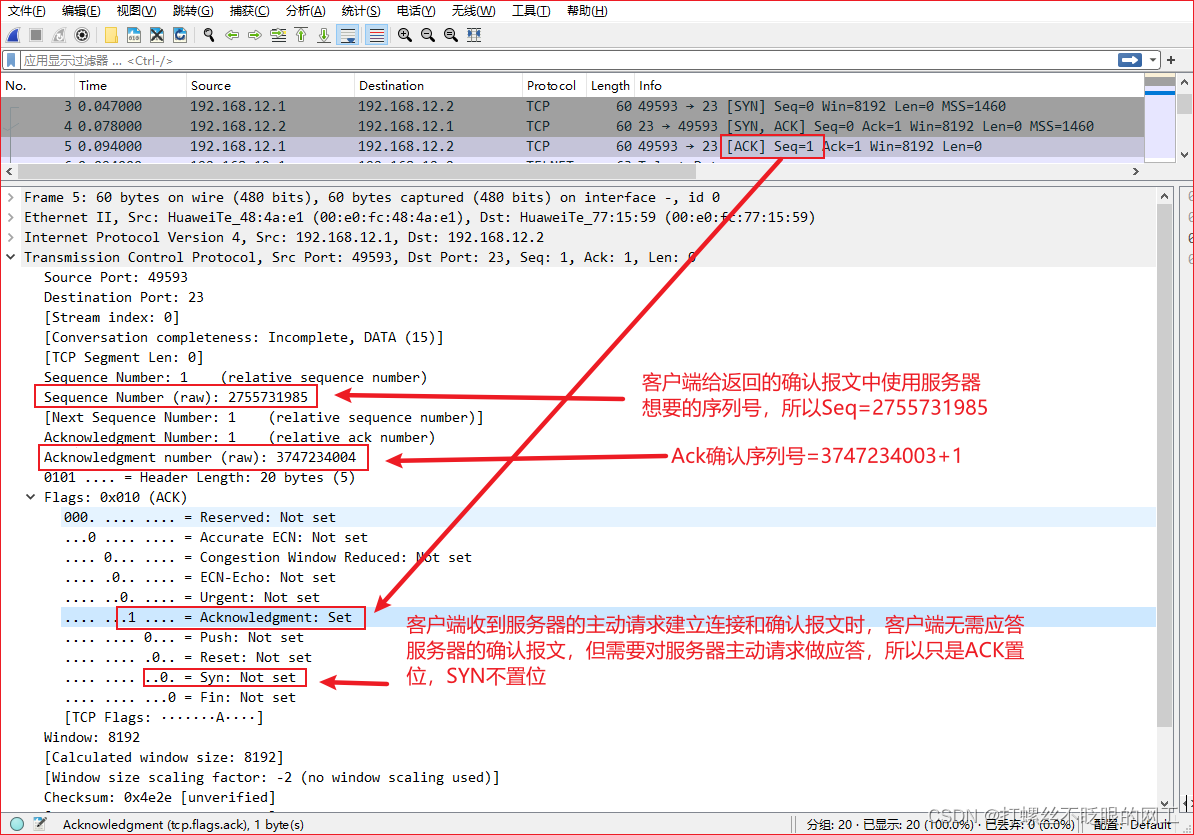
握手成功后,服务器(12.2)开始发送数据,共发送了四次,第一、二次都是9字节,第三、四次分别是28字节和11字节,所以总共发了9+9+28+11=57字节
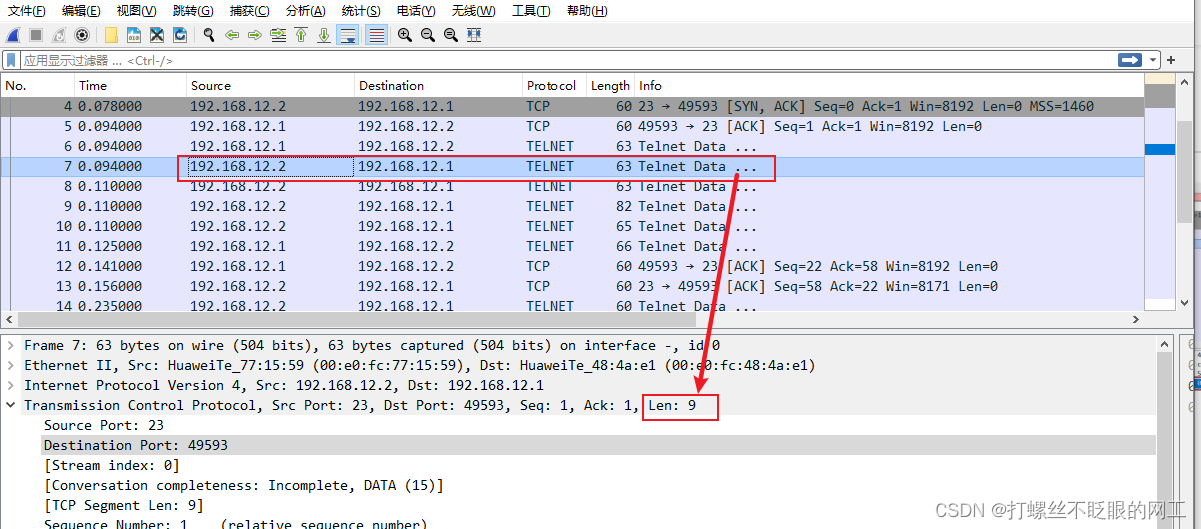
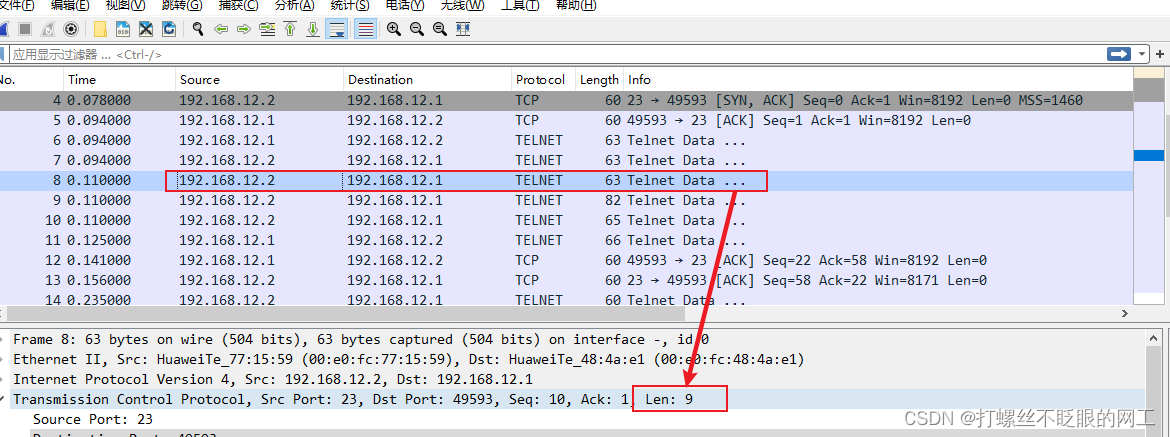
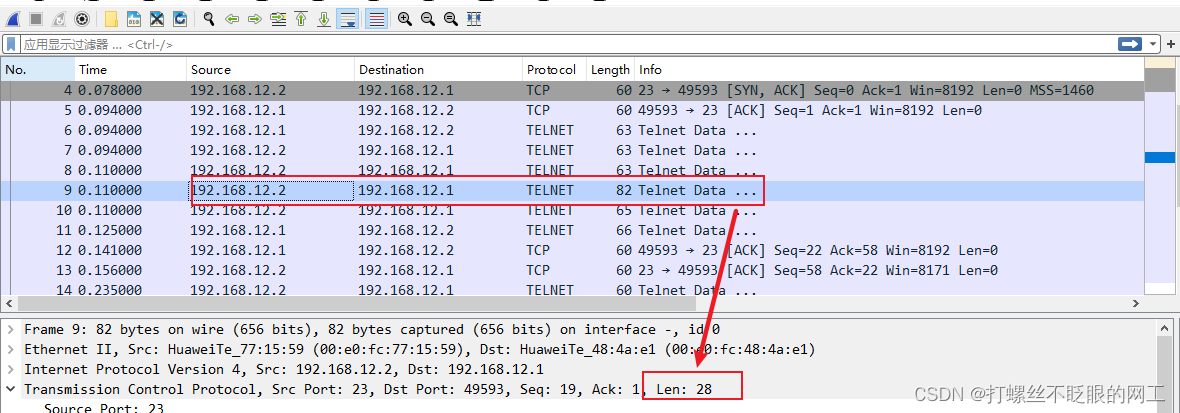
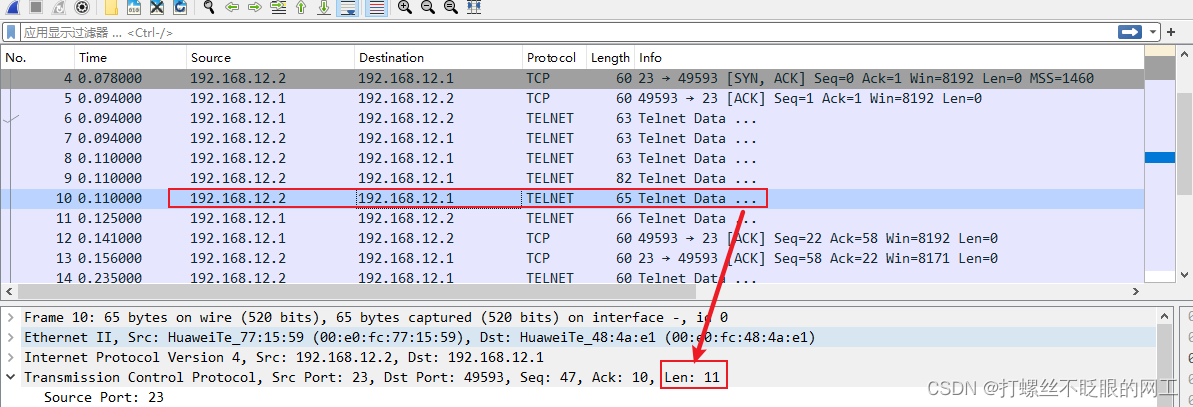
当客户端(12.1)收到服务器发送的数据后,回复一个Ack确认报文,予以确认,发送ACK为57+1
四次挥手
当数据传输完成,TCP需要通过“四次挥手”机制断开TCP连接,释放系统资源。
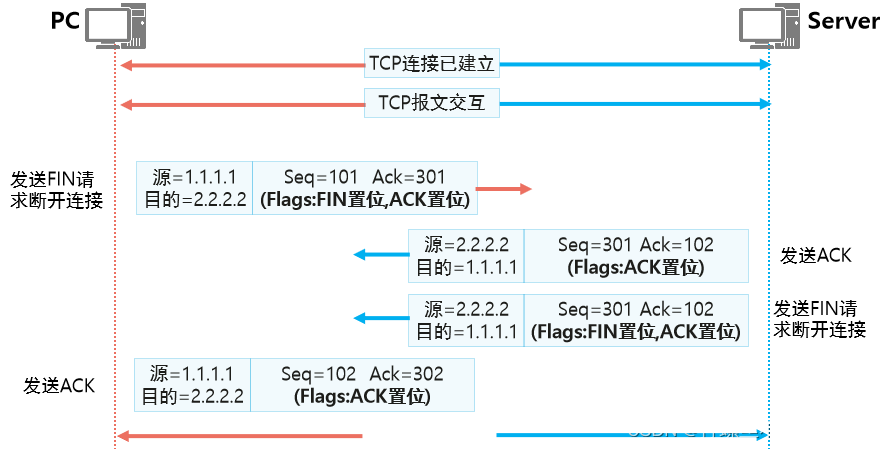
- 由PC1发出一个FIN字段置”1 ”的不带数据的TCP段;
- PC2收到PC1发来的FIN置位的TCP报文后,会回复一个ACK置位的TCP报文。
- 若PC2也没有需要发送的数据,则直接发送FIN置位的TCP报文。假设此时PC2还有数据要发送,那么当PC2发送完这些数据之后会发送一个FIN置位的TCP报文去关闭连接。
- PC1收到FIN置位的TCP报文,回复ACK报文,TCP双向连接断开。
TCP支持全双工模式传输数据,这意味着同一时刻两个方向都可以进行数据的传输。在传输数据之前,TCP通过三次握手建立的实际上是两个方向的连接,因此在传输完毕后,两个方向的连接必须都关闭。
相关文章:

TCP三次握手/四次挥手
TCP三次握手 任何基于TCP的应用,在发送数据之前,都需要由TCP进行“三次握手”建立连接示意图 第一次握手:客户端PC发送一个SYN位置1(SYN1代表请求服务端建立连接)的TCP报文发送给要建立TCP连接的Server,此…...

Python程序员看见一个好看的手机壁纸网站,开撸!
人生苦短,我用python 最近好像没什么大事, .那就采集一下小——姐——姐————看下吧~ python 安装包资料:点击此处跳转文末名片获取 最近有同学的爬虫代码出了bug,给问我怎么改 于是就发现了这个好看的手机壁纸网站。 这个图片应该是违规…...
浏览器工作原理
一、JavaScript 的历史 JavaScript(简称JS)Web前端开发的脚本语言。 它诞生1995年,由网景公司的 Brendan Eich 开发。最初,JavaScript 被设计用于在网页上嵌入动态内容和交互式功能。 1996年,JavaScript 1.1 成为国…...

对在使用容器HashSet存放自定义对象时重写其类的hashcode和equals方法的几点认识
判断是否是相同对象时,hashcode和equals方法的调用顺序 先调用hashcode()方法,再调用equals()方法如果hashcode()方法得到的哈希值不同,那么两个对象一定不相同,不作后续判断如果hashcode()方法得到的哈希值相同,那么…...

Java集群:单体架构升级到集群架构(二)实现session共享
默认情况下,session是保存在TOMCAT服务器内存中的,如果我们有两个TOMCAT,它们的session是没有共享的。我们这回要做的就是把session保存在redis中,这样两个TOMCAT就可以共享session了。其实这货的详细原理还是很复杂的,…...

MySQL索引及索引失效的分析(MySQL8.0.19)
目录索引数据结构主键索引非主键索引索引在什么时候是有效的?字符串比较大小btween and索引数据结构 主键索引 我们先来看看索引的数据结构,以及我们是如何利用索引来搜索数据的。MySQL的数据存储结构是B树,在叶子节点存储了数据行ÿ…...

第一个 Django 应用
1. 创建项目 1.1 新建项目 首先新建一个项目,名为 mysite,命令如下: django-admin startproject mysite # 或用 django-admin.py运行成功,生成一些目录: mysite/manage.py # 管理 Django 项目的命令行工具mysit…...

001-ksum 求符合条件的 k 个数 1. Two Sum/15. 3Sum/18. 4Sum/
推荐阅读 000-从零开始的数据结构与算法 001-01-ksum 求符合条件的 k 个数 1. Two Sum/15. 3Sum/18. 4Sum/ 002-两数相加 add two numbers 003-无重复字符的最长子串 Longest Substring Without Repeating Characters 004-寻找两个正序数组的中位数 005-最长回文子串 Lon…...

Nginx学习笔记(三)Linux环境下Nginx的安装和部署
目录一、官网下载二、配置基本信息1.上传 Linux2.解压3.安装编译环境4.配置基本信息4.1 配置失败原因(1):没有安装C编译环境4.2 配置失败原因(2):没有安装 PCRE 依赖4.3 配置失败原因(3):没有安装 zlib 依赖5.查看文件列表三、编译安装四、配…...

【十二天学java】day05--数组和循环高级
**# 1.数组 概念: 指的是一种容器,可以同来存储同种数据类型的多个值。 但是数组容器在存储数据的时候,需要结合隐式转换考虑。 比如: 定义了一个int类型的数组。那么boolean。double类型的数据是不能存到这个数组中的&#…...
)
用队列实现栈和用栈实现队列(C 语言)
目录 一、用队列实现栈 二、 用栈实现队列 一、用队列实现栈 请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。 实现 MyStack 类: void push(int…...
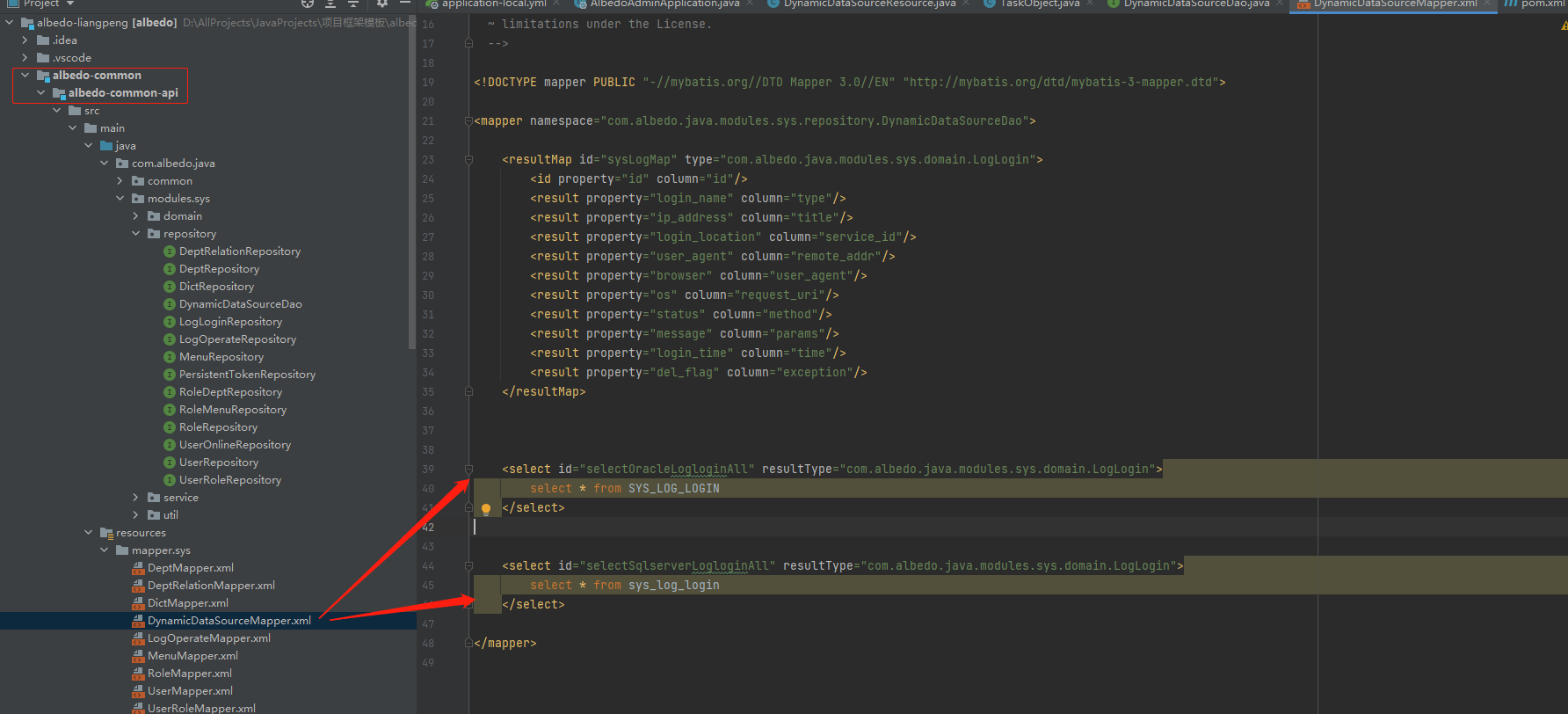
albedo开源框架配置多数据源
前言:公司框架项目一直都没认真阅读过,最近项目需要连接oracle数据,所以尝试使用框架连接多数据库。添加多数据源插件:我们在项目的插件模块内添加多数据源插件:albedo-dynamic-datasource<?xml version"1.0&…...
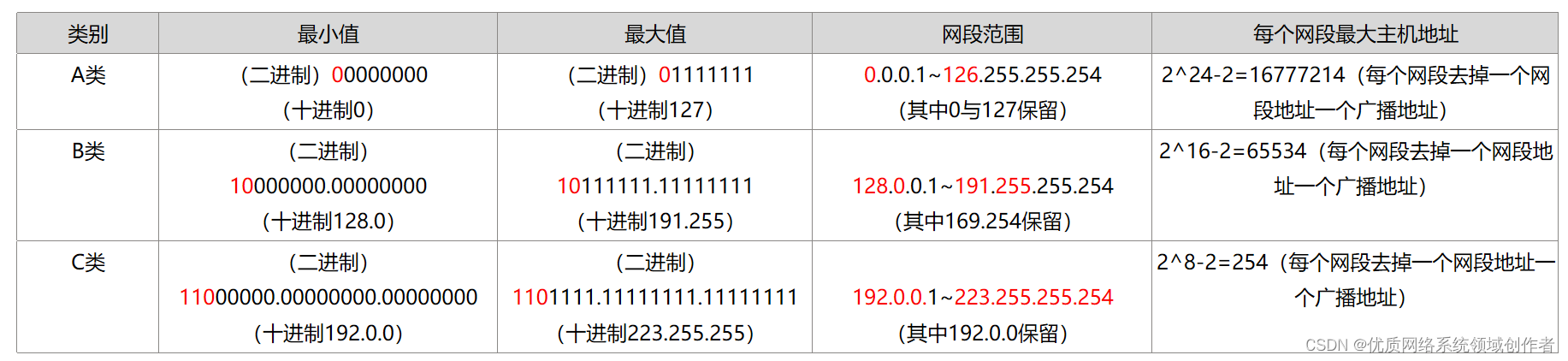
22张图带你了解IP地址有什么作用
了解IP地址 1、IP地址的格式 在IP协议的报文中,可以得知IP地址是有32个比特,IP地址在计算机中是以二进制的方式处理的,如果全部以二进制的形式来表示,使用跟表达都非常的困难,所以为了人类方便记忆,采用了…...
121.Android 简单的人工智能聊天项目,chatAi,AI聊天项目,GPTAi
//首页xml布局代码: <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"mat…...

C++ this指针详解
this 是 C 中的一个关键字,也是一个 const 指针,它指向当前对象,通过它可以访问当前对象的所有成员。所谓当前对象,是指正在使用的对象。例如对于stu.show();,stu 就是当前对象,this 就指向 stu。下面是使用…...
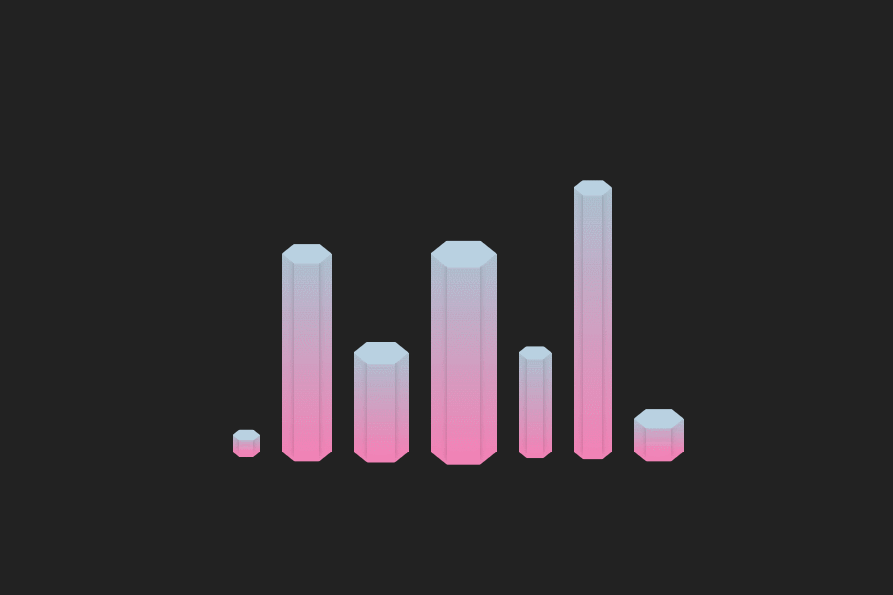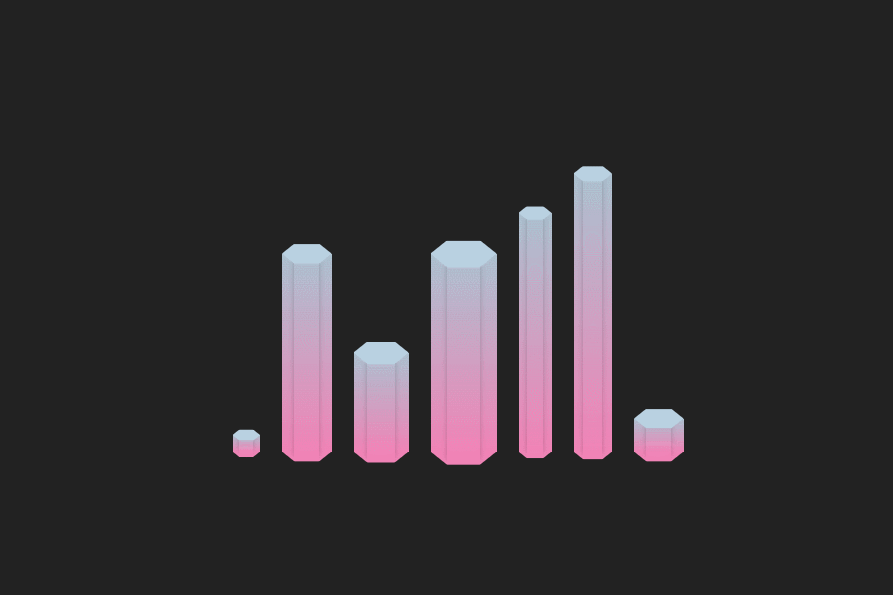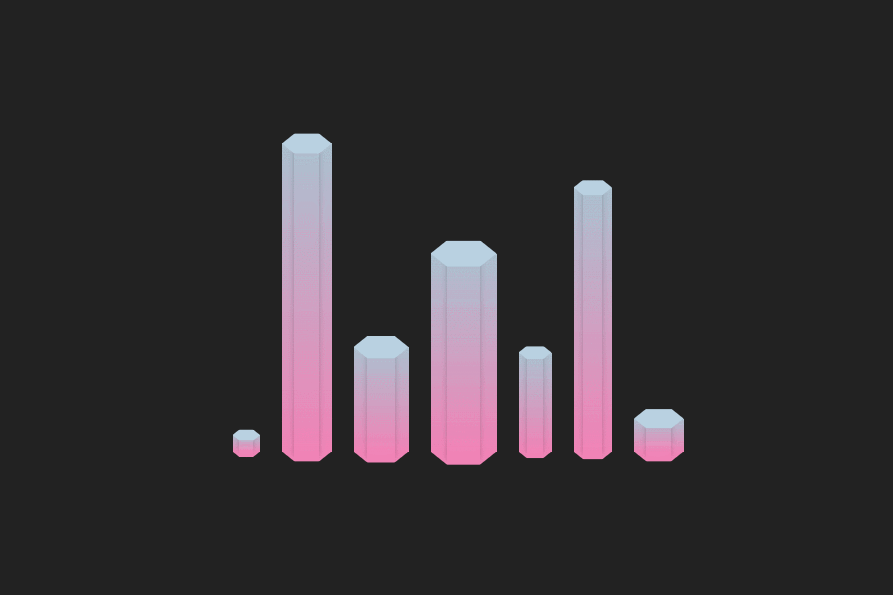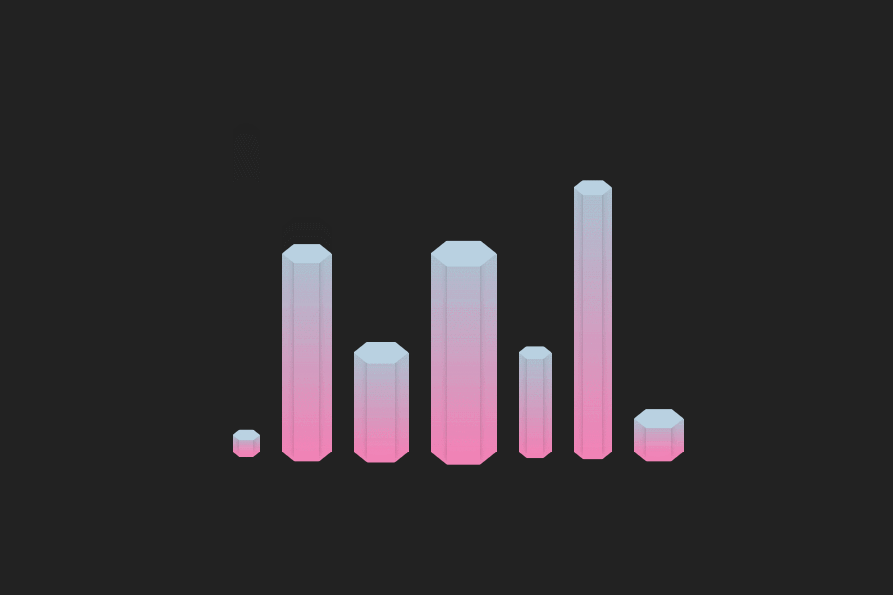
CSS 实现六边形柱状图
前言 👏CSS 实现六边形柱状图 速速来Get吧~ 🥇文末分享源代码。记得点赞关注收藏! 1.实现效果 2.实现步骤 定义全局css变量,柱状宽度为–w,最大高度为–h,柱形整体为渐变色,定义上部分颜色为…...
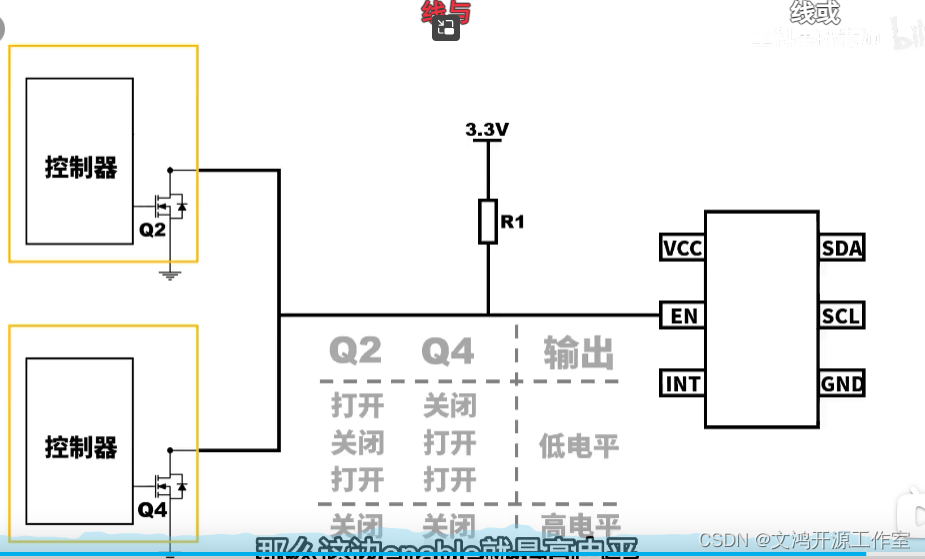
什么是推挽输出,开漏输出?
这篇文章是看B站“工科男孙老师”这个视频的笔记推挽 开漏 高阻 这都是谁想出来的词?? 我觉得讲的很好,做一下笔记 1.什么是IO输出三态 一共有:高电平, 低电平,浮空/高阻态 三种IO态 2.推挽输出 推挽输出能够表示高、…...
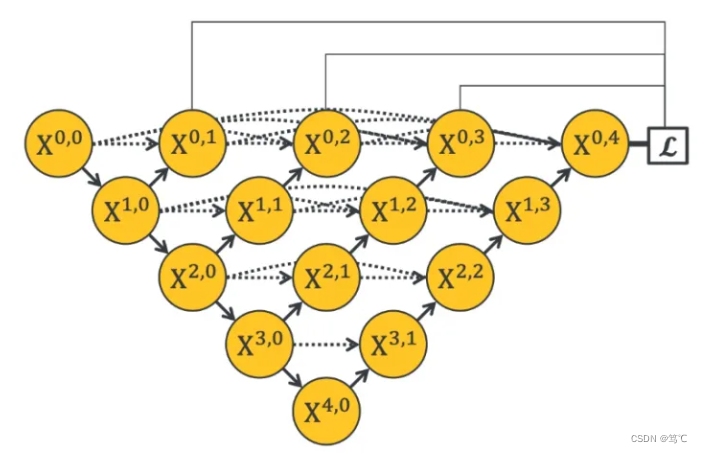
【图像分割】Unet系列深度讲解(FCN、UNET、UNET++)
【图像分割】Unet 深度讲解 文章目录【图像分割】Unet 深度讲解1. 介绍1.1 背景介绍:1.2 医学图像特点1.3 图像分割是什么2. Unet发展历程(FCN、Unet、Unet)2.1 全卷积网络-FCN2.1.1 FCN介绍:2.1.2 FCN框架2.1.3 反卷积层2.1.4 输…...
list底层的简单实现(万字长文详解!)
list底层的简单实现 文章目录list底层的简单实现list_node的实现!list_node的构造函数list的迭代器!——重点!list迭代器的成员变量迭代器的构造函数* 重载前置 重载后置 重载前置-- 重载后置-- 重载! 重载 重载-- 重载list的const迭代器——…...

学习Linux只要学会这个命令就够了!
大家好,我是良许。 这段时间又是搬家,又是找新办公室,现在终于安顿下来了,有时间给大家分享干货了。 今天给大家介绍一个 Linux 超级实用命令,有了这个命令,你就可以愉快使用 Linux 上几乎所有常用命令了…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...