回溯排列+棋盘问题篇--代码随想录算法训练营第二十三天| 46.全排列,47.全排列 II,51. N皇后,37. 解数独
46.全排列
题目链接:. - 力扣(LeetCode)
讲解视频:
组合与排列的区别,回溯算法求解的时候,有何不同?
题目描述:
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1] 输出:[[1]]
解题思路:
与前边的组合,分割问题不同在于全排列问题每次递归至下一层后都要从头开始遍历。使用一个used数组进行去重,判断当前元素是否已经被使用

代码:
class Solution {
public:vector<vector<int>> result;vector<int> path;void backTracking(vector<int>& nums, vector<int>& used){if(path.size() == nums.size()) {result.push_back(path);return;}for(int i = 0; i < nums.size(); i++){if(used[i] == 0){used[i] = 1;path.push_back(nums[i]);backTracking(nums,used);path.pop_back();used[i] = 0;}}}vector<vector<int>> permute(vector<int>& nums) {result.clear();path.clear();vector<int> used(nums.size(), 0);backTracking(nums,used);return result;}
};47.全排列 II
题目链接:. - 力扣(LeetCode)
讲解视频:
回溯算法求解全排列,如何去重?| LeetCode:47.全排列 II
题目描述:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]
示例 2:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
解题思路:
先对nums数组排序,去重逻辑:
- 横向去重:使用used数组对同层元素进行判断,若前后元素相同且前一个元素used值为0(表明当前遍历是同层遍历),就说明该元素已经被使用,跳过这个元素;
- 纵向去重:每次递归至下一层后都要从头开始遍历。使用同一个used数组进行去重,判断当前元素是否已经被使用

代码:
class Solution {
public:vector<vector<int>> result;vector<int> path;void backTracking(vector<int>& nums,vector<int>& used){if(path.size() == nums.size()) {result.push_back(path);return;}for(int i = 0; i < nums.size(); i++){if(i > 0 && nums[i] == nums[i-1] && used[i-1] == 0) continue;if(used[i] == 0){path.push_back(nums[i]);used[i] = 1;backTracking(nums,used);used[i] = 0;path.pop_back();}}}vector<vector<int>> permuteUnique(vector<int>& nums) {result.clear();path.clear();sort(nums.begin(),nums.end());vector<int> used(nums.size(),0);backTracking(nums,used);return result;}
};51. N皇后
题目链接:. - 力扣(LeetCode)
讲解视频:
这就是传说中的N皇后? 回溯算法安排!| LeetCode:51.N皇后
题目描述:
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
解题思路:
N皇后问题步骤:
- 按行遍历,对每一行中每一个位置做判断,看当前棋盘布局是否符合条件;
- 判断标准:同一行,同一列,对角线(45°,135°)均不能存在2个及以上的Q;
- 若所有行均遍历完成,就把结果保存至result中,并返回。

代码:
class Solution {
public:vector<vector<string>> result;bool isValid(vector<string>& chessboard, int row, int col, int n){for(int i = 0; i < row; i++) // 判断列if(chessboard[i][col] == 'Q') return false;for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--,j--) //对角45°if(chessboard[i][j] == 'Q') return false;for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--,j++) //对角135°if(chessboard[i][j] == 'Q') return false;return true;}void backTracking(vector<string>& chessboard, int row, int n){if(row == n){result.push_back(chessboard);return;}for(int col = 0; col < n; col++){if(isValid(chessboard,row,col,n)){chessboard[row][col] = 'Q';backTracking(chessboard,row+1,n);chessboard[row][col] = '.';}}}vector<vector<string>> solveNQueens(int n) {vector<string> chessboard(n,string(n,'.'));backTracking(chessboard,0,n);return result;}
};37. 解数独
题目链接:. - 力扣(LeetCode)
讲解视频:
回溯算法二维递归?解数独不过如此!| LeetCode:37. 解数独
题目描述:
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。题目数据 保证 输入数独仅有一个解
示例 1:

输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

解题思路:
该题目与N皇后问题的区别在于:
- 解数独问题中只要找到一个解即可,回溯函数类型为bool。N皇后问题找到所有解,回溯函数类型为void;
- 解数独问题使用二维数组遍历。N皇后问题使用一维数组遍历。
- 解数独问题中每一个格中从1~9中判断。N皇后问题每一个格只从Q判断
- 解数独问题判断条件:同行同列不能有重复元素,3x3宫内不能有重复元素

代码:
class Solution {
public:bool isValid(int row, int col, int k, vector<vector<char>>& board){for(int i = 0; i < board[0].size(); i++) //判断行if(i != col && board[row][i] == k) return false; for(int i = 0; i < board.size(); i++) //判断列if(i != row && board[i][col] == k) return false; for(int i = row - row % 3; i < row - row % 3 + 3; i++)for(int j = col - col % 3; j < col - col%3 + 3; j++)if(i != row && j != col && board[i][j] == k) return false;return true;}bool backTracking(vector<vector<char>>& board){for(int i = 0; i < board.size(); i++){for(int j = 0; j < board[0].size(); j++){if(board[i][j] == '.'){for(char k = '1'; k <= '9'; k++){if(isValid(i,j,k,board)){board[i][j] = k;if(backTracking(board)) return true;board[i][j] = '.';}}return false;}}}return true;}void solveSudoku(vector<vector<char>>& board) {backTracking(board);}
};相关文章:

回溯排列+棋盘问题篇--代码随想录算法训练营第二十三天| 46.全排列,47.全排列 II,51. N皇后,37. 解数独
46.全排列 题目链接:. - 力扣(LeetCode) 讲解视频: 组合与排列的区别,回溯算法求解的时候,有何不同? 题目描述: 给定一个不含重复数字的数组 nums ,返回其 所有可能…...

ESXI加入VMware现有集群提示常规性错误
集群内有vSphere6.5和6.7的版本,都开启了EVC 这台老服务器是DELL R710添加时报错,网上查了些资料说要重装ESXI或者关闭EVC等等 最终解决方法是,给这台ESXI配置一个NTP服务器,同步系统时间,之后即可正常加入集群 往期文…...

数字噪音计(声级计)【AR814数字噪音计】
系统介绍 声级计,又叫噪音计,是噪声测量中最基本的仪器。声级计一般由电容式传声器、前置放大器、衰减器、放大器、频率计权网络以及有效值指示表头等组成。 声级计的工作原理是:由传声器将声音转换成电信号,再由前置放大器放大…...

【Vue3】图片未加载成功前占位
背景 在写项目时,加载图片未成功前,会出现空白页面,太影响美观和体验感 解决方案 1. element ui通过slot占位符解决 2. 自定义指令 原生img标签可以通过自定义指令解决,img标签有onload和onerror事件,都是在渲染成…...

AbstractQueuedSynchronizer之AQS
目录 AQS简单入门为什么说AQS是JUC包下的重要基石AQS能干嘛?实际实现原理AQS自身成员变量Node内部类的成员变量源码解读总结 AQS简单入门 AQS是抽象的队列同步器,是用来实现锁或者其它同步器组件的公共基础部分的抽象实现,是重量级基础框架及…...

<数据集>起重机识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:2984张 标注数量(xml文件个数):2984 标注数量(txt文件个数):2984 标注类别数:1 标注类别名称:[cranes] 使用标注工具:labelImg 标注规则:对…...
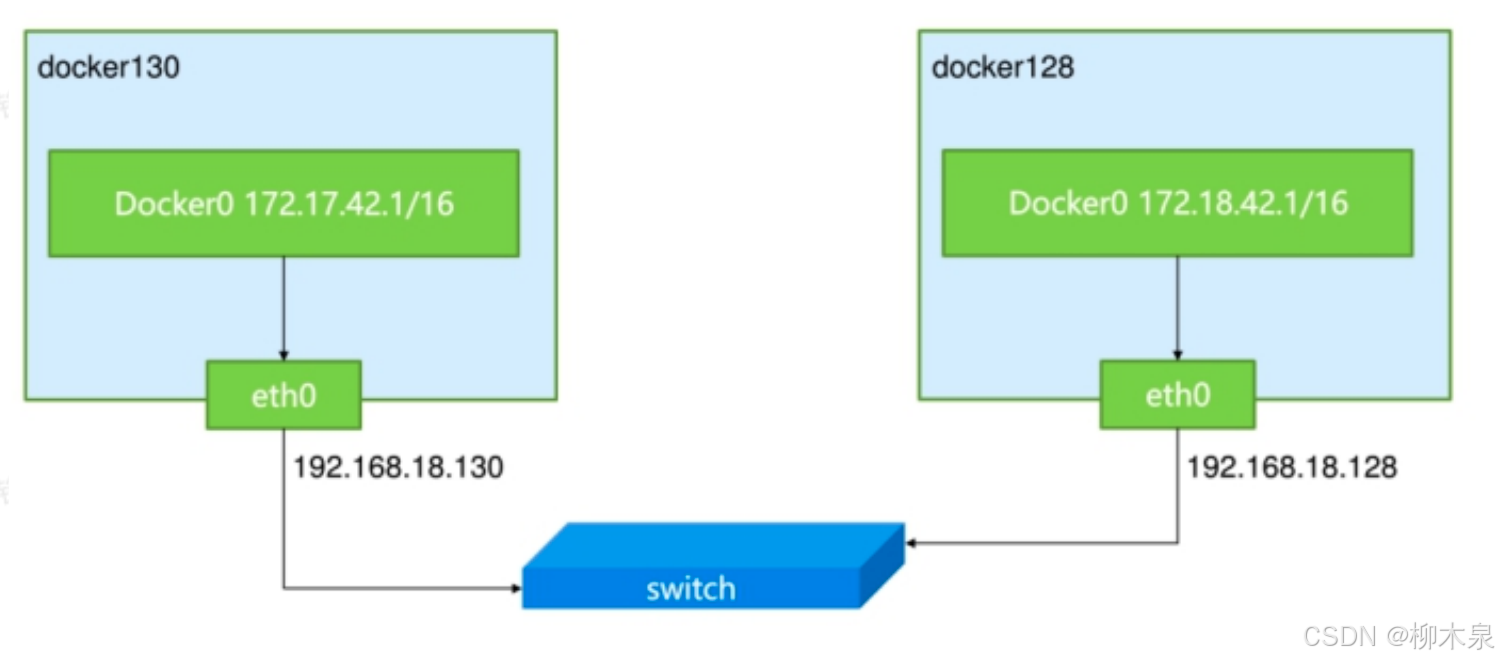
04--Docker
前言:前面写过关于DockerKubernetes的部署,主要是针对国产化linux系统的适配问题,并没有对docker进行复习。这里整理一下docker的知识点,用作容器化微服务的起点,主要为日常工作配置使用,本章可能有点长&am…...

MiniCPM-V: A GPT-4V Level MLLM on Your Phone 手机上的 GPT-4V 级多模态大模型
GitHub - OpenBMB/MiniCPM-V: MiniCPM-V 2.6: A GPT-4V Level MLLM for Single Image, Multi Image and Video on Your Phone 2408.01800 (arxiv.org) 目录 Introduction Model Architecture Training End-side Deployment MiniCPM-V是一种高效的多模态大型语言模型&…...

Unity初识
1:下载Unity Hub 下载地址:Unity官方下载_Unity最新版_从Unity Hub下载安装 | Unity中国官网 建议直接使用unity hub因为支持比较全面,适合新手 有中文 管理 编辑器等等功能支持 下载安装不过多介绍 2:Unity Hub汉化 因为我…...

【游戏引擎之路】登神长阶(九)——《3D游戏编程大师技巧》:我想成为游戏之神!
5月20日-6月4日:攻克2D物理引擎。 6月4日-6月13日:攻克《3D数学基础》。 6月13日-6月20日:攻克《3D图形教程》。 6月21日-6月22日:攻克《Raycasting游戏教程》。 6月23日-7月1日:攻克《Windows游戏编程大师技巧》。 7月…...

Linux:线程同步之信号量
信号量 (1)What(什么是信号量) 提供一种计数器的方式控制对共享资源的访问;当计数器大于0时,请求资源成功并计数器-1;当计数器小于0时,线程阻塞,等待其它线程执行signal(V操作&…...

GPT-SoVITS-文本转语音(你的声音不再是唯一)
本文将要介绍GPT-SoVITS的安装和使用方法 首先感谢花儿不哭大佬带来的RVC声音克隆 花儿不哭: 花儿不哭的个人空间-花儿不哭个人主页-哔哩哔哩视频 (bilibili.com) GPT-SoVITS下载地址 GitHub - RVC-Boss/GPT-SoVITS: 1 min voice data can also be used to train a …...

C语言深度剖析(部分)--剩下随缘更新
C语言深度剖析 关键字auto-最宽容大度的关键字 变量的分类 代码块:用{ }括起来的区域 局部变量:包含在代码块中的变量,局部变量具有临时性,进入代码块,自动形成局部变量,退出代码块自动释放。 全局变量…...

计算机毕业设计选题推荐-电缆行业生产管理系统-Java/Python项目实战
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

Linux 下查看 CPU 使用率
目录 一、什么是 CPU 使用率二、查看 CPU 利用率1、使用 top 查看2、用 pidstat 查看3、用 ps 查看4、用 htop 查看5、用 nmon 查看6、用 atop 查看7、用 glances 查看8、用 vmstat 查看9、用 sar 查看10、dstat11、iostat 三、总结 CPU 使用率是最直观和最常用的系统性能指标&…...

数理基础知识
数理基础 大数定律期望方差常见分布伯努利分布泊松分布高斯分布服从一维高斯分布的随机变量KL散度服从多元高斯分布的随机变量KL散度 Gibbs不等式凸函数Jensen不等式 似然函数泰勒近似信息论信息量信息熵KL散度JS散度交叉熵 Wiener ProcessSDE 大数定律 期望方差 x为连续随机…...

Java解决lombok和mapstruct编译模块的问题
pom.xml <dependencies><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><!-- 1.18.16版本 --><version>${lombok.version}</version><scope>provided</scope><!-- 防…...

大模型场景应用全集:持续更新中
一、应用场景 1.办公场景 智能办公:文案生成(协助构建大纲优化表达内容生成)、PPT美化(自动排版演讲备注生成PPT)、数据分析(生成公式数据处理表格生成)。 智能会议:会议策划&…...
)
理解RabbitMQ中的消息存储机制:非持久化、持久化与惰性队列(Lazy Queue)
文章目录 1. 非持久化消息(Transient Messages)内存压力处理 2. 持久化消息(Persistent Messages)3. 惰性队列(Lazy Queue)官方推荐 总结 在RabbitMQ中,消息的存储和处理方式可以根据不同的需求…...

【机器学习】BP神经网络正向计算
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 BP神经网络正向计算1. 引言2. BP神经网络结构回顾3. 正向计算的基本原理4. 数学…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
