概率论原理精解【9】
文章目录
- 集类
- 拓扑空间
- 基
- 参考文献
集类
- C是一个集类(以G的某些子集为元素的集合称为G的集类)。
- A i ∈ C , ∩ i = 1 n A i ∈ C , 此为有限交封闭 C 所得集类 C ∩ f A_i \in C,\cap_{i=1}^nA_i \in C,此为有限交封闭C所得集类C_{\cap f} Ai∈C,∩i=1nAi∈C,此为有限交封闭C所得集类C∩f
- A n ∈ C , n ≥ 1 , ∩ n A n ∈ C , 此为可列交封闭 C 所得集类 C δ A_n \in C,n \ge 1,\cap_{n}A_n \in C,此为可列交封闭C所得集类C_{\delta} An∈C,n≥1,∩nAn∈C,此为可列交封闭C所得集类Cδ
- C Σ f 称为有限不交并封闭 C 所得集类 C_{\Sigma f}称为有限不交并封闭C所得集类 CΣf称为有限不交并封闭C所得集类
- ∪ i = 1 n A i ∈ C , 此为有限并封闭 C 所得集类 C ∪ f \cup_{i=1}^nA_i \in C,此为有限并封闭C所得集类C_{\cup f} ∪i=1nAi∈C,此为有限并封闭C所得集类C∪f
- C σ 为可列并封闭 C 所得集类 C_{\sigma}为可列并封闭C所得集类 Cσ为可列并封闭C所得集类
- C Σ σ 为可列不交并封闭 C 所得集类 C_{\Sigma\sigma}为可列不交并封闭C所得集类 CΣσ为可列不交并封闭C所得集类
- 1. 如果 C 对有限交封闭,称为 π 类 2. 如果 ∅ ∈ C ,且有 A , B ∈ C = > A ∩ B ∈ C , A \ B ∈ C Σ f , C 称为半环。 3. C 是半环,且 G ∈ C , C 是半代数。 4. C 对有限交和取余集运算封闭,且 G ∈ C , ∅ ∈ C , C 称为代数或域。 5. C 对可列交和取余集运算封闭,且 G ∈ C , ∅ ∈ C , C 称为 σ 代数 6. C 对单调序列极限封闭, C 称为单调类 7. C 称为 λ 类,则: ( 1 ) G ∈ C ( 2 ) A , B ∈ C , B ⊂ A = > A \ B ∈ C ( 3 ) A n ∈ C , n ≥ 1 , A n ↑ A = > A ∈ C 1.如果C对有限交封闭,称为\pi类 \\2.如果\emptyset \in C,且有A,B \in C=>A\cap B \in C,A \backslash B \in C_{\Sigma f},C称为半环。 \\3.C是半环,且G \in C,C是半代数。 \\4.C对有限交和取余集运算封闭,且G \in C,\empty \in C,C称为代数或域。 \\5.C对可列交和取余集运算封闭,且G \in C,\empty \in C,C称为\sigma代数 \\6.C对单调序列极限封闭,C称为单调类 \\7.C称为\lambda类,则: \\(1)G \in C \\(2)A,B \in C , B \subset A=>A \backslash B \in C \\(3) A_n \in C,n \ge 1,A_n \uparrow A => A \in C 1.如果C对有限交封闭,称为π类2.如果∅∈C,且有A,B∈C=>A∩B∈C,A\B∈CΣf,C称为半环。3.C是半环,且G∈C,C是半代数。4.C对有限交和取余集运算封闭,且G∈C,∅∈C,C称为代数或域。5.C对可列交和取余集运算封闭,且G∈C,∅∈C,C称为σ代数6.C对单调序列极限封闭,C称为单调类7.C称为λ类,则:(1)G∈C(2)A,B∈C,B⊂A=>A\B∈C(3)An∈C,n≥1,An↑A=>A∈C
- 对 G 上的任一非空集类 F , 存在包含 F 的最小 σ 代数、 λ 类和单调类, 记为 σ ( F ) 、 λ ( F ) 和 m ( F ) , m ( F ) ⊂ λ ( F ) ⊂ σ ( F ) 对G上的任一非空集类F,存在包含F的最小\sigma代数、\lambda类和单调类,\\记为\sigma(F)、\lambda(F)和m(F),m(F)\subset \lambda(F) \subset \sigma(F) 对G上的任一非空集类F,存在包含F的最小σ代数、λ类和单调类,记为σ(F)、λ(F)和m(F),m(F)⊂λ(F)⊂σ(F)
C 为一集类, 1. 若 C 为代数,则 m ( C ) = σ ( C ) 2. 若 C 为一 π 类,则 λ ( C ) = σ ( C ) C为一集类, \\1.若C为代数,则m(C)= \sigma (C) \\2.若C为一\pi类,则\lambda(C)= \sigma (C) C为一集类,1.若C为代数,则m(C)=σ(C)2.若C为一π类,则λ(C)=σ(C)
-
设 C 和 F 为两个集类,且 C ⊂ F 1. 若 C 为代数, F 为单调类,则 σ ( C ) ⊂ F 2. 若 C 为 π 类,且 F 为 λ 类,则 σ ( C ) ⊂ F 设C和F为两个集类,且C \subset F \\1.若C为代数,F为单调类,则\sigma(C) \subset F \\2.若C为\pi类,且F为\lambda类,则\sigma(C) \subset F 设C和F为两个集类,且C⊂F1.若C为代数,F为单调类,则σ(C)⊂F2.若C为π类,且F为λ类,则σ(C)⊂F
-
C 为一集类, 1. 若要 m ( C ) = σ ( C ) ,则必须且只需 A ∈ C = > A c ∈ m ( C ) , A , B ∈ C = > A ∩ B ∈ m ( C ) 2. 若要 λ ( C ) = σ ( C ) ,必须且只需 A , B ∈ C = > A ∩ B ∈ λ ( C ) C为一集类, \\1.若要m(C)= \sigma (C),则必须且只需 \\A \in C=>A^c \in m(C),A,B \in C=>A \cap B \in m(C) \\2.若要\lambda(C)=\sigma(C),必须且只需 \\A,B \in C => A \cap B \in \lambda (C) C为一集类,1.若要m(C)=σ(C),则必须且只需A∈C=>Ac∈m(C),A,B∈C=>A∩B∈m(C)2.若要λ(C)=σ(C),必须且只需A,B∈C=>A∩B∈λ(C)
-
C 为一集类,若它满足下列条件之一,则有 m ( C ) = σ ( C ) 1. A , B ∈ C = > A ∩ B ∈ C , A ∈ C = > A c ∈ C δ 2. A , B ∈ C = > A ∪ B ∈ C , A ∈ C = > A c ∈ C δ C为一集类,若它满足下列条件之一,则有m(C)=\sigma(C) \\1.A,B \in C=>A \cap B \in C,A \in C=>A^c \in C_{\delta} \\2.A,B \in C=>A \cup B \in C,A \in C=>A^c \in C_{\delta} C为一集类,若它满足下列条件之一,则有m(C)=σ(C)1.A,B∈C=>A∩B∈C,A∈C=>Ac∈Cδ2.A,B∈C=>A∪B∈C,A∈C=>Ac∈Cδ
拓扑空间
基
- 设 X 为非空集合, β ⊂ P ( X ) 设X为非空集合,\beta \subset P(X) 设X为非空集合,β⊂P(X)
1. 若 β 是 X 上某拓扑的基,则 ( 1 ) ∪ B ∈ β B = X ( 2 ) 若 B 1 、 B 2 ∈ β 且 x ∈ B 1 ∩ B 2 ,则 ∃ B x ∈ β , s . t . x ∈ β , x ∈ B x ⊂ B 1 ∩ B 2 2. 若 β 满足 ( 1 ) 和 ( 2 ) ,则存在唯一的拓扑 τ = { G ⊂ X : ∃ β G ⊂ β , s . t . G = ∪ B ∈ β G B } 以 β 为基,并称这个拓扑是以 β 为基生成的拓扑。 1.若\beta 是X上某拓扑的基,则 \\(1)\cup_{B \in \beta}B=X \\(2)若B_1、B_2 \in \beta且x \in B_1\cap B_2,则\exists B_x \in \beta,s.t. x \in \beta,x \in B_x \subset B_1\cap B_2 \\2.若\beta满足(1)和(2),则存在唯一的拓扑 \\\tau=\{G \subset X:\exists \beta_G \subset \beta ,s.t.G=\cup_{B\in \beta_G}B\} \\以\beta为基,并称这个拓扑是以\beta为基生成的拓扑。 1.若β是X上某拓扑的基,则(1)∪B∈βB=X(2)若B1、B2∈β且x∈B1∩B2,则∃Bx∈β,s.t.x∈β,x∈Bx⊂B1∩B22.若β满足(1)和(2),则存在唯一的拓扑τ={G⊂X:∃βG⊂β,s.t.G=∪B∈βGB}以β为基,并称这个拓扑是以β为基生成的拓扑。 - 设 β 是拓扑空间 X 的一个基,若 β 是可数的,则称 X 具有可数基 设\beta是拓扑空间X的一个基,若\beta是可数的,则称X具有可数基 设β是拓扑空间X的一个基,若β是可数的,则称X具有可数基
- 例题
下面内容由文心一言自动生成
拓扑空间是数学中的一个重要概念,它允许我们在不考虑距离和角度的具体度量下,研究空间的几何性质和变换。在拓扑空间中,“基”通常指的是一组特定的开集,这些开集的并集能够生成整个空间上的拓扑结构。以下是一个关于拓扑空间基的例题:题目:设 X X X是一个集合, X X X上的一组子集 B \mathcal{B} B满足以下条件:
- B \mathcal{B} B中的任意两个元素的交集可以表示为 B \mathcal{B} B中某些元素的并集。
- X X X可以表示为 B \mathcal{B} B中某些元素的并集。
证明:由 B \mathcal{B} B生成的拓扑空间 ( X , T ) (X, \mathcal{T}) (X,T)中, B \mathcal{B} B是 T \mathcal{T} T的一个基。
证明:
- 定义由 B \mathcal{B} B生成的拓扑:
首先,我们定义由 B \mathcal{B} B生成的拓扑 T \mathcal{T} T。设 T \mathcal{T} T是包含 B \mathcal{B} B的最小集合,且满足以下条件:
- ∅ ∈ T \emptyset \in \mathcal{T} ∅∈T(空集是任何拓扑的一部分)。
- 如果 U 1 , U 2 , … ∈ T U_1, U_2, \ldots \in \mathcal{T} U1,U2,…∈T,则 ⋃ i = 1 ∞ U i ∈ T \bigcup_{i=1}^\infty U_i \in \mathcal{T} ⋃i=1∞Ui∈T(任意多个开集的并集是开集)。
- 如果 U 1 , U 2 ∈ T U_1, U_2 \in \mathcal{T} U1,U2∈T,则 U 1 ∩ U 2 ∈ T U_1 \cap U_2 \in \mathcal{T} U1∩U2∈T(有限多个开集的交集是开集)。
由于 B \mathcal{B} B满足题目中的条件,且我们要求 T \mathcal{T} T是最小的这样的集合,因此可以通过不断添加由 B \mathcal{B} B中元素通过并集和有限交集运算得到的集合来构造 T \mathcal{T} T。
证明 B \mathcal{B} B是 T \mathcal{T} T的基:
根据拓扑空间基的定义,一个集合 B \mathcal{B} B是拓扑空间 ( X , T ) (X, \mathcal{T}) (X,T)的基,如果对于 T \mathcal{T} T中的任意元素 U U U(即任意开集),都存在 B \mathcal{B} B中的元素 B 1 , B 2 , … B_1, B_2, \ldots B1,B2,…(可能有无穷多个),使得 U = ⋃ i = 1 ∞ B i U = \bigcup_{i=1}^\infty B_i U=⋃i=1∞Bi。
现在,对于 T \mathcal{T} T中的任意元素 U U U,由于 U ∈ T U \in \mathcal{T} U∈T,且 T \mathcal{T} T是由 B \mathcal{B} B通过并集和有限交集运算得到的,因此我们可以使用归纳法(或超限归纳法,如果涉及到无穷多个集合)来证明 U U U可以由 B \mathcal{B} B中的元素通过并集得到。具体来说,如果 U U U本身就是 B \mathcal{B} B中的元素,则结论显然成立。如果 U U U不是 B \mathcal{B} B中的元素,则 U U U必然是通过并集和有限交集运算从 B \mathcal{B} B中的元素得到的。由于并集和有限交集运算可以相互转化(即,可以通过并集和补集运算来表示有限交集),我们可以最终将 U U U表示为 B \mathcal{B} B中某些元素的并集。
注意:这里的证明依赖于 B \mathcal{B} B满足题目中的条件,特别是第一个条件(任意两个元素的交集可以表示为某些元素的并集),这保证了在通过并集和有限交集运算构造 T \mathcal{T} T时,不会超出由 B \mathcal{B} B生成的集合范围。
结论:
因此,我们证明了由 B \mathcal{B} B生成的拓扑空间 ( X , T ) (X, \mathcal{T}) (X,T)中, B \mathcal{B} B是 T \mathcal{T} T的一个基。
注意
- 这个例题是一个较为抽象的证明题,旨在理解拓扑空间基的概念和性质。
- 在实际应用中,拓扑空间的基往往是具体给出的,例如实数集上的开区间集合是实数集上标准拓扑的一个基。
- 拓扑空间的基不是唯一的,但不同的基会生成相同的拓扑结构。
- 几个 拓扑空间基的例子
由文心一言自动生成
- 成为拓扑空间基的具体条件
以下内容由文心一言自动生成
成为拓扑空间基的条件主要基于拓扑基的定义和性质。以下是成为拓扑空间基的具体条件:1. 覆盖性
- 条件描述:基中的元素(开集)的并集必须等于整个拓扑空间。这确保了拓扑空间中的每一个点都至少被一个基元素所覆盖。
- 数学表达:设 B \mathcal{B} B是拓扑空间 X X X的一个子集族,如果 ⋃ B ∈ B B = X \bigcup_{B\in\mathcal{B}}B=X ⋃B∈BB=X,则满足覆盖性条件。
2. 有限交性质
- 条件描述:对于基中任意两个元素的交集,如果这个交集非空,则必须存在基中的另一个元素,它是这两个元素交集的子集。这保证了通过基元素可以“精细地”构造出拓扑空间中的所有开集。
- 数学表达:对于任意 B 1 , B 2 ∈ B B_1, B_2\in\mathcal{B} B1,B2∈B,如果 B 1 ∩ B 2 ≠ ∅ B_1\cap B_2\neq\emptyset B1∩B2=∅,则存在 B 3 ∈ B B_3\in\mathcal{B} B3∈B,使得 B 3 ⊆ B 1 ∩ B 2 B_3\subseteq B_1\cap B_2 B3⊆B1∩B2。
3. 生成的拓扑
- 条件描述(隐含):基中元素的并集可以生成拓扑空间中的所有开集。具体来说,对于拓扑空间 X X X的任意子集 U U U,如果 U U U可以表示为基中某些元素的并集,则 U U U是开集。
- 数学表达:设 T \mathcal{T} T是由基 B \mathcal{B} B生成的拓扑,则对于任意 U ⊆ X U\subseteq X U⊆X,如果 U = ⋃ i ∈ I B i U=\bigcup_{i\in I}B_i U=⋃i∈IBi,其中 I I I是某个指标集,且对于所有 i ∈ I i\in I i∈I,有 B i ∈ B B_i\in\mathcal{B} Bi∈B,则 U ∈ T U\in\mathcal{T} U∈T。
4. 唯一性(非必须,但重要性质)
- 条件描述:虽然不同的基可能生成相同的拓扑,但在某些情况下,我们可能希望找到一个“最小”或“最自然”的基。这通常与拓扑空间的特定性质或结构有关。
- 注意:唯一性不是成为拓扑空间基的必要条件,但它对于理解和描述拓扑空间的结构非常重要。
总结
成为拓扑空间基的条件主要包括覆盖性和有限交性质。这两个条件确保了基元素能够“有效地”覆盖整个拓扑空间,并通过并集和有限交的方式生成出所有的开集。同时,虽然唯一性不是必要条件,但寻找最小或最自然的基对于理解和应用拓扑空间具有重要意义。
- 更多例子及证明 在拓扑学中,拓扑空间的基(也称为拓扑基)是一个重要的概念,它用于描述拓扑空间中的开集族,这些开集族能够生成整个拓扑空间的所有开集。以下是几个具体的拓扑空间基的例子及其详细解释和证明。
- 拓扑空间基的充要条件
成为拓扑空间基的充要条件可以归纳如下:
以下内容由文心一言自动生成
设 ( X , T ) (X, \mathcal{T}) (X,T)是一个拓扑空间, B ⊆ T \mathcal{B} \subseteq \mathcal{T} B⊆T是 T \mathcal{T} T的一个子集族。则 B \mathcal{B} B是 T \mathcal{T} T的一组拓扑基的充要条件是:
覆盖性:
- ⋃ B ∈ B B = X \bigcup_{B \in \mathcal{B}} B = X ⋃B∈BB=X。即,基中所有元素的并集等于整个拓扑空间。这保证了拓扑空间中的每一个点都至少被一个基元素所覆盖。
有限交性质(或称为“局部有限性”的某种形式):
- 对于任意 x ∈ X x \in X x∈X和任意包含 x x x的开集 U ∈ T U \in \mathcal{T} U∈T,存在 B ∈ B B \in \mathcal{B} B∈B使得 x ∈ B ⊆ U x \in B \subseteq U x∈B⊆U。这实际上是有限交性质在点集拓扑中的具体体现,它确保了通过基元素可以“精细地”构造出拓扑空间中的所有开集。更一般地,这也意味着对于任意两个基元素 B 1 , B 2 ∈ B B_1, B_2 \in \mathcal{B} B1,B2∈B(如果它们的交集非空),则对于交集中的任意点 x x x,都存在另一个基元素 B ∈ B B \in \mathcal{B} B∈B,使得 x ∈ B ⊆ B 1 ∩ B 2 x \in B \subseteq B_1 \cap B_2 x∈B⊆B1∩B2。然而,这一表述更侧重于点的视角,而非直接描述交集的有限性。
这个条件实际上隐含了有限交性质的一种形式,即对于任意两个基元素的交集(如果非空),在交集中的每一点附近都可以找到一个更小的基元素来“细化”这个交集。然而,这个条件更侧重于从点的视角来描述基的性质。生成性(隐含于定义中):
- 拓扑空间 T \mathcal{T} T中的任意开集都可以表示为基 B \mathcal{B} B中某些元素的并集。这是拓扑基定义的自然结果,也是它被称为“基”的原因。
证明思路(简要)
- 必要性:假设 B \mathcal{B} B是 T \mathcal{T} T的一组拓扑基。
- 覆盖性:由拓扑基的定义直接得出。
- 有限交性质:对于任意 x ∈ X x \in X x∈X和任意开集 U ∋ x U \ni x U∋x,由于 U U U是开集,且 B \mathcal{B} B是拓扑基,根据拓扑基的性质,存在 B ∈ B B \in \mathcal{B} B∈B使得 x ∈ B ⊆ U x \in B \subseteq U x∈B⊆U。
- 充分性:假设 B \mathcal{B} B满足上述两个条件。
- 验证生成性:对于任意开集 U ∈ T U \in \mathcal{T} U∈T,由于 B \mathcal{B} B满足覆盖性,对于任意 x ∈ U x \in U x∈U,存在 B x ∈ B B_x \in \mathcal{B} Bx∈B使得 x ∈ B x ⊆ U x \in B_x \subseteq U x∈Bx⊆U。因此, U = ⋃ x ∈ U B x U = \bigcup_{x \in U} B_x U=⋃x∈UBx,即 U U U可以表示为基中元素的并集。
注意事项
- 有限交性质在这里的表述侧重于点的视角,而非直接描述交集的有限性。在更一般的上下文中,有限交性质可能涉及更复杂的交集结构。
- 生成性是拓扑基定义的自然结果,通常不需要单独作为充要条件的一部分来验证。然而,在理解拓扑基的概念时,它是非常重要的。
- 不同的教材或文献中,对拓扑基的定义和性质的表述可能略有不同,但核心思想是一致的。
- 几个拓扑空间基的证明例子
拓扑空间的基是拓扑学中一个核心概念,它用于描述拓扑空间中的开集族,这些开集族满足特定条件,能够生成整个拓扑空间的所有开集。以下是几个拓扑空间的基的例子及其详细解释证明:
例子1:度量空间的球形邻域基
描述:设 ( X , ρ ) (X,\rho) (X,ρ)是度量空间,其中 ρ \rho ρ是度量函数。则所有的球形邻域 { B ( x , r ) ∣ x ∈ X , r > 0 } \{B(x,r)|x\in X, r>0\} {B(x,r)∣x∈X,r>0}(其中 B ( x , r ) B(x,r) B(x,r)表示以 x x x为中心, r r r为半径的开球)构成 X X X的一组拓扑基。
证明:
- 条件一验证:对于任意 x ∈ X x\in X x∈X,存在 r > 0 r>0 r>0(例如取 r = 1 r=1 r=1),使得 x ∈ B ( x , r ) x\in B(x,r) x∈B(x,r),即每个点都被至少一个基元素包含。
- 条件二验证:对于任意两个基元素 B ( x 1 , r 1 ) B(x_1,r_1) B(x1,r1)和 B ( x 2 , r 2 ) B(x_2,r_2) B(x2,r2),以及任意 y ∈ B ( x 1 , r 1 ) ∩ B ( x 2 , r 2 ) y\in B(x_1,r_1)\cap B(x_2,r_2) y∈B(x1,r1)∩B(x2,r2),存在某个 r > 0 r>0 r>0(例如取 r = min { r 1 − d ( x 1 , y ) , r 2 − d ( x 2 , y ) } r=\min\{r_1-d(x_1,y), r_2-d(x_2,y)\} r=min{r1−d(x1,y),r2−d(x2,y)},其中 d ( x 1 , y ) d(x_1,y) d(x1,y)和 d ( x 2 , y ) d(x_2,y) d(x2,y)分别表示 x 1 x_1 x1到 y y y和 x 2 x_2 x2到 y y y的距离,注意这里需要 r 1 , r 2 r_1, r_2 r1,r2足够大使得 r r r为正数),使得 y ∈ B ( y , r ) ⊂ B ( x 1 , r 1 ) ∩ B ( x 2 , r 2 ) y\in B(y,r)\subset B(x_1,r_1)\cap B(x_2,r_2) y∈B(y,r)⊂B(x1,r1)∩B(x2,r2)。这是因为度量空间中的开球具有嵌套性质。
例子2:离散空间的单点集基
描述:设 X X X是任意集合,赋予离散拓扑,则所有单点集 { { x } ∣ x ∈ X } \{\{x\}|x\in X\} {{x}∣x∈X}构成 X X X的一组拓扑基。
证明:
- 条件一验证:对于任意 x ∈ X x\in X x∈X,显然有 { x } ∈ { { x } ∣ x ∈ X } \{x\}\in \{\{x\}|x\in X\} {x}∈{{x}∣x∈X},即每个点都被一个单点集包含。
- 条件二验证:对于任意两个单点集 { x 1 } \{x_1\} {x1}和 { x 2 } \{x_2\} {x2},如果它们有交集(即 x 1 = x 2 x_1=x_2 x1=x2),则它们的交集就是 { x 1 } \{x_1\} {x1}(或 { x 2 } \{x_2\} {x2}),此时可以取 { x 1 } \{x_1\} {x1}(或 { x 2 } \{x_2\} {x2})作为满足条件的基元素。如果它们没有交集,则不需要考虑,因为条件二只要求对于有交集的基元素成立。
例子3:实数集的下限拓扑基
描述:设 R \mathbb{R} R是实数集,令 B = { [ a , b ) ∣ a , b ∈ R , a < b } \mathcal{B}=\{[a,b)|a,b\in\mathbb{R},a<b\} B={[a,b)∣a,b∈R,a<b},则 B \mathcal{B} B是 R \mathbb{R} R的一组拓扑基,它定义的拓扑称为下限拓扑。
证明:
- 条件一验证:对于任意 x ∈ R x\in\mathbb{R} x∈R,可以取 [ x − 1 , x ) ∈ B [x-1,x)\in\mathcal{B} [x−1,x)∈B,使得 x ∈ [ x − 1 , x ) x\in[x-1,x) x∈[x−1,x)。
- 条件二验证:对于任意两个基元素 [ a 1 , b 1 ) [a_1,b_1) [a1,b1)和 [ a 2 , b 2 ) [a_2,b_2) [a2,b2),以及任意 y ∈ [ a 1 , b 1 ) ∩ [ a 2 , b 2 ) y\in[a_1,b_1)\cap[a_2,b_2) y∈[a1,b1)∩[a2,b2),可以取 [ y , min { b 1 , b 2 } ) ∈ B [y, \min\{b_1,b_2\})\in\mathcal{B} [y,min{b1,b2})∈B,使得 y ∈ [ y , min { b 1 , b 2 } ) ⊂ [ a 1 , b 1 ) ∩ [ a 2 , b 2 ) y\in[y, \min\{b_1,b_2\})\subset[a_1,b_1)\cap[a_2,b_2) y∈[y,min{b1,b2})⊂[a1,b1)∩[a2,b2)。
总结
以上三个例子展示了不同类型的拓扑空间及其对应的基。在证明过程中,我们主要验证了基的两个基本条件:
- 每个点都被至少一个基元素包含
- 任意两个基元素的交集可以通过某个基元素来“细化”。
- 这些基元素共同生成了拓扑空间中的所有开集。
参考文献
1.文心一言
2.《测度论基础与高等概率论》
3.《测度论讲义》第三版
相关文章:

概率论原理精解【9】
文章目录 集类拓扑空间基 参考文献 集类 C是一个集类(以G的某些子集为元素的集合称为G的集类)。 A i ∈ C , ∩ i 1 n A i ∈ C , 此为有限交封闭 C 所得集类 C ∩ f A_i \in C,\cap_{i1}^nA_i \in C,此为有限交封闭C所得集类C_{\cap f} Ai∈C,∩i1n…...
-C++应用程序将onnx模型编译并转成tensorrt可执行模型)
Pytorch添加自定义算子之(11)-C++应用程序将onnx模型编译并转成tensorrt可执行模型
一、环境 参考 opencv tensorrt cuda visual studio 2019 cmake 二、CMakeLists.txt配置文件 CMAKE_MINIMUM_REQUIRED(VERSION 2.8)PROJECT(segment)set(CMAKE_CXX_FLAGS "-std=c++14 -O1")link_directories(/usr/local/cuda/lib64) # set(OpenCV_DIR "/opt/…...

C++笔记1•C++入门基础•
1.C关键字 C总计63个关键字,C语言32个关键字: 2.命名空间: 在 C/C 中,变量、函数和后面要学到的类都是大量存在的,这些变量、函数和类的名称将都存在于全局作用域中,可能会导致很多冲突。使用命名空间的目…...

Linux查看系统线程数
Linux查看系统线程数 查看线程数查看进程内的线程统计线程数 查看线程数 想要查看Linux操作系统允许的最大线程数,可以通过命令 ulimit -a返回配置项的详细说明: # core文件的最大值为100blocks core file size (blocks, -c) 0# 进程的数…...

【Python基础】Python六种标准数据类型中哪些是可变数据,哪些是不可变数据
文章目录 1.基本介绍可变数据类型不可变数据类型2.可变和不可变到底指的是什么?可变(Mutable)不可变(Immutable)总结1.基本介绍 Python 中的六种标准数据类型分为可变数据类型和不可变数据类型。以下是这些数据类型的分类: 可变数据类型 列表(List) 列表是一种有序集…...

android13去掉安全模式 删除安全模式
总纲 android13 rom 开发总纲说明 目录 1.前言 2.问题排查 3.修改方法 3.1方法1 3.2方法2 4.测试 5.彩蛋 1.前言 Android设备上的安全模式是一种诊断模式,当设备无法正常启动时,它会启动到这个模式。在这个模式下,只有系统自带的程序和服务会被运行,所有的第三方…...

LeetCode239 滑动窗口最大值
前言 题目: 239. 滑动窗口最大值 文档: 代码随想录——滑动窗口最大值 编程语言: C 解题状态: 没有思路,困难题,恐怖如斯 思路 本题的关键在于对单调队列的应用,时间复杂度 O ( n ) O(n) O(n)限…...

文件解析漏洞—IIS解析漏洞—IIS7.X
在IIS7.0和IIS7.5版本下也存在解析漏洞,在默认Fast-CGI开启状况下,在一个文件路径/xx.jpg后面加上/xx.php会将 “/xx.jpg/xx.php” 解析为 php 文件 利用条件 php.ini里的cgi.fix_pathinfo1 开启IIS7在Fast-CGI运行模式下 在 phpstudy2018 根目录创建…...
))
vue中子传父之间通信(this.$emit触发父组件方法和.sync修饰符与$emit(update:xxx))
文章目录 前言一、通过this.$emit触发父组件方法实现二、.sync修饰符与$emit(update:xxx) 前言 看了几篇帖子,都没有将$emit两种用法汇聚总结在一起。需要额外的浪费时间去查看其他帖子,索性自己总结一下,方便以后查看。 一、通过this.$emit…...

SocketIO 的 html 代码示例
话不多说,以下为前端 SocketIO 代码示例 <!DOCTYPE html> <html> <head><meta http-equiv"Content-Type" content"text/html; charsetutf-8"/><title>TestConnect</title><base><script src&quo…...

Vercel Error: (Azure) OpenAI API key not found
题意:Vercel 错误:(Azure) OpenAI API 密钥未找到 问题背景: I implemented openAI API in my Next.js app with the help of langchain library and it works superb on localhost, but in Vercel (ProVersion) it throws an error: 我使用…...

SPSS、Python员工满意度问卷调查激励保健理论研究:决策树、随机森林和AdaBoost|附代码数据
全文链接:https://tecdat.cn/?p37293 原文出处:拓端数据部落公众号 在深入了解公司当前的实际情况和员工内心真实想法的基础上,我们旨在从专业视角出发,为企业在组织管理方面的不足进行诊断,并进行全面审视。 为了…...

常见深度学习优化器总结
Adam 是一种非常流行的优化器,因为它结合了动量和自适应学习率的优点,通常在大多数情况下表现良好。不过,如果你在使用 Adam 时遇到性能问题或希望进一步调优,以下是几种可以考虑的替代优化器: 1. AdamW (Adam with W…...

python并发编程之多线程和多进程
了解过python 编程语言的人,可能很多人都听过,python的多线程是假的。 之所以这么说的原因是因为,大家应该都知道python 是一门解释型语言,在cpython解释器中有一个GIL(Global Interpreter Lock),全局解释锁ÿ…...

gorm入门——根据条件查询列表
在 GORM 中,你可以通过 Where 方法结合多个条件来查询符合条件的记录列表。Where 方法支持 AND 和 OR 条件,并且可以链式调用以构建复杂的查询。 示例代码: 假设你有一个 User 结构体,并希望根据多个条件查询符合条件的记录列表…...

笔面试编程题总结
8/6诺瓦星云 修改程序 void point(int *p){*p p[2];}; int main() {int c[] {1,2,3,4,5},*p c;point(p1);for(;p <c5;){printf("%d",*p);}return 0; }1、分隔字符串 strtok //c语言 #include <stdio.h> #include <string.h>// 函数声明 char* fin…...

[other][知识]八大行星的英文各是什么?
1、水星英文名 Mercury,水星最接近太阳,是太阳系中体积和质量最小的行星; 2、金星英文名 Venus,太阳系中第六大行星,太阳系中温度最高的行星,中国古代称之为太白或太白金星; 3、地球英文 E…...
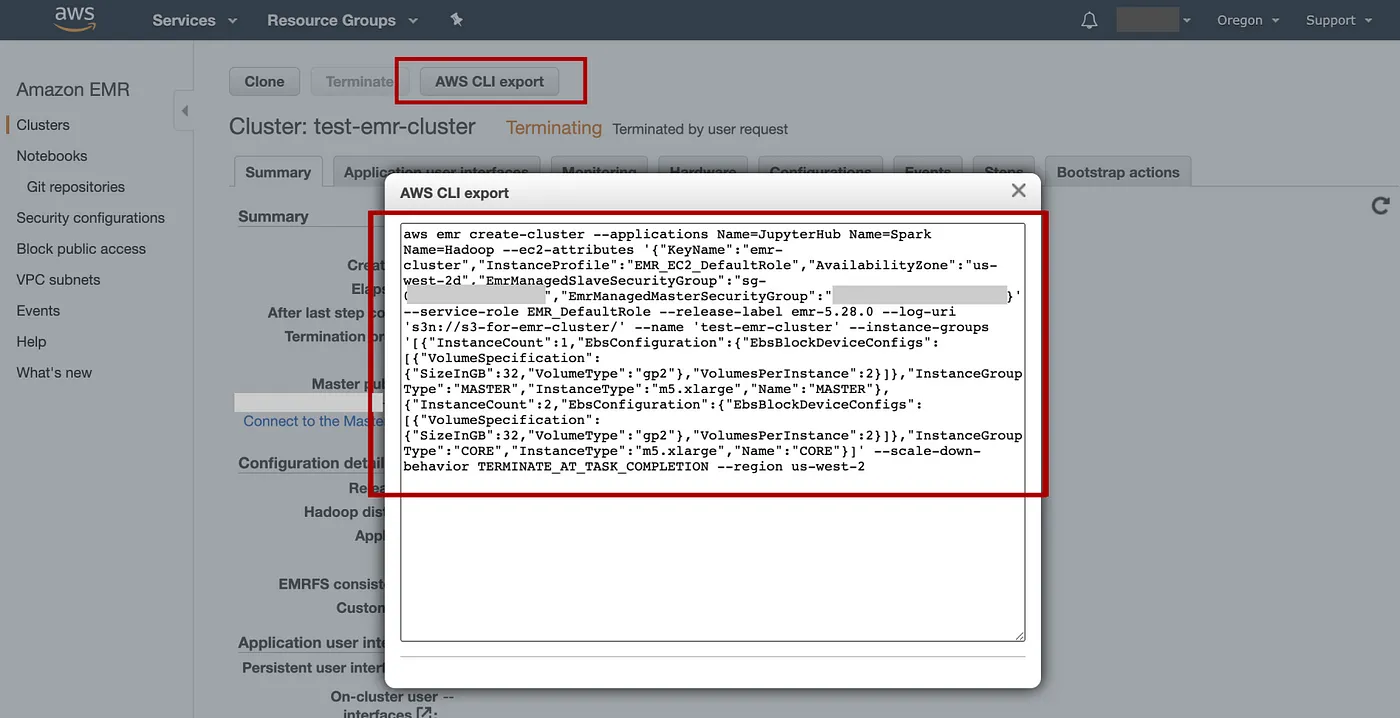
如何使用 AWS CLI 创建和运行 EMR 集群
为初学者提供清晰易懂的教程 为初学者提供清晰易懂的教程 Apache Spark 和 AWS EMR 上的 Spark 集群 添加图片注释,不超过 140 字(可选) 欢迎来到雲闪世界。Spark 被认为是“大数据丛林之王”,在数据分析、机器学习、流媒体和图形…...

HDFS写入数据的流程图
1.客户端向namenode发送请求,请示写入数据 2.namenode接受请求后,判断这个用户是否有写入权限,如果不具备直接报错;如果有写入权限,接着判断在要写入的目录下是否已经存在这个文件,如果存在,直…...

【Material-UI】使用指南:快速入门与核心功能解析
文章目录 一、快速入门1.1 安装和导入1.2 组件的独立性 二、全局设置2.1 响应式元标签2.2 CssBaseline2.3 默认字体 三、响应式设计3.1 Grid系统 四、最佳实践4.1 组件的一致性4.2 性能优化4.3 可访问性 五、总结 Material-UI是一个功能强大且灵活的React UI框架,为…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
