Gitlab仓库的权限分配以及如何查看自己的权限
在GitLab中,权限分配和查看自己的权限可以通过以下步骤进行:
### 1. 查看自己的权限
要查看你在某个GitLab项目中的权限,可以按照以下步骤操作:
1. 登录到GitLab。
2. 进入你想查看权限的项目页面。
3. 在左侧菜单中,点击“Members”(成员)。
4. 在成员列表中,你可以看到自己和其他成员的权限级别。
### 2. 权限级别
GitLab中的权限级别从低到高依次为:
- **Guest**:只能查看项目的公开内容。
- **Reporter**:可以查看和克隆代码,但不能推送代码。
- **Developer**:可以查看、克隆和推送代码。
- **Maintainer**:可以管理项目设置和成员。
- **Owner**:拥有项目的所有权限(仅限于个人项目)。
### 3. 分配权限
如果你是项目的Maintainer或Owner,可以按照以下步骤分配权限:
1. 登录到GitLab。
2. 进入你想管理的项目页面。
3. 在左侧菜单中,点击“Members”(成员)。
4. 点击“Invite members”(邀请成员)按钮。
5. 输入成员的用户名或邮箱地址。
6. 选择适当的权限级别(Guest、Reporter、Developer、Maintainer)。
7. 点击“Invite”按钮。
相关文章:

Gitlab仓库的权限分配以及如何查看自己的权限
在GitLab中,权限分配和查看自己的权限可以通过以下步骤进行: ### 1. 查看自己的权限 要查看你在某个GitLab项目中的权限,可以按照以下步骤操作: 1. 登录到GitLab。 2. 进入你想查看权限的项目页面。 3. 在左侧菜单中,…...
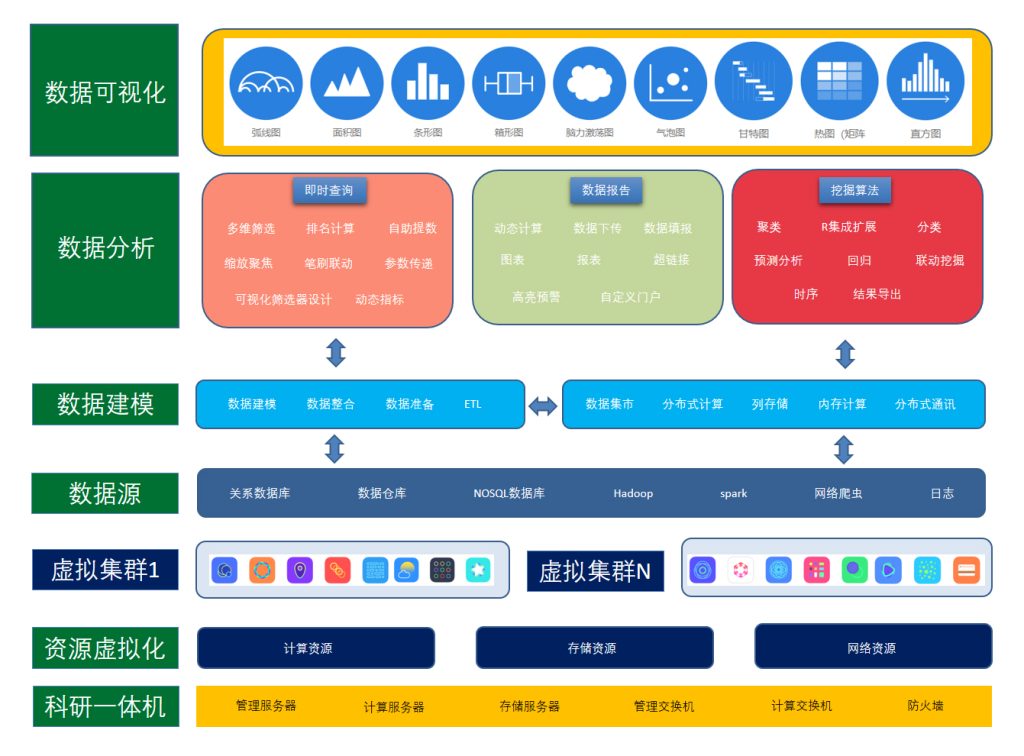
职业本科大数据实训室
一、职业本科大数据实训室建设背景 在数字化浪潮汹涌澎湃的今天,大数据已跃升为引领社会进步和经济发展的新引擎。随着《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》的深入实施,数字化转型作为国家战略的重要组成部分&…...

【密码学】网络攻击类型:窃听攻击、假冒攻击、欺骗攻击和重放攻击
一、窃听攻击、假冒攻击、欺骗攻击和重放攻击的定义 这些攻击从名字中就大概能知道他们的攻击原理,我就不赘述了,直接用一个表格来一次性介绍四种攻击方式。 攻击类型攻击原理窃听攻击攻击者监听网络中的数据传输以获取敏感信息。示例:在未加…...

探索WebKit的奥秘:塑造高效、兼容的现代网页应用
探索WebKit的奥秘:塑造高效、兼容的现代网页应用 在数字时代的洪流中,网页应用已成为连接用户与信息的桥梁,其性能、兼容性和用户体验直接决定了产品的成败。WebKit,作为众多现代浏览器背后的核心渲染引擎,承载着将HT…...

2-52 基于matlab局部信息的模糊C均值聚类算法(FLICM)
基于matlab局部信息的模糊C均值聚类算法(FLICM),是在FCM聚类算法的基础上结合了图像的邻域信息,有更好的鲁棒性。程序已调通,可直接运行。 2-52 局部信息的模糊C均值聚类算法 - 小红书 (xiaohongshu.com)...

JAVASE
1.泛型 泛型指类型参数化, 在定义期间,不知道调用时会使用什么类型,就可以添加泛型形参,在使用时传入实参固定类型即可。 泛型类: 泛型应用在类上。 一般用在类名后,用尖括号括起来。用大写字母作为泛型参…...

SpringBoot学习之EasyExcel解析合并单元格(三十九)
本解析主要采用反射来修改EasyExcel 返回的默认数据结构实现。 一、待解析表格 二、依赖 全部pom.xml文件如下,仅作参考: <project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLo…...

【Kimi学习笔记】C/C++、C#、Java 和 Python
C/C、C#、Java 和 Python 是几种流行的编程语言,它们在设计哲学、用途、语法和运行机制上有所不同。下面我会类比 Java 来解释这些语言的区别: 1. C/C: 类比于 Java,C/C 是一种更接近硬件的低级语言,提供了更多的控制…...

基于贪心算法的路径优化
贪心算法原理 贪心算法的核心原理是在每一步选择中都采取在当前看来最好的选择,以期达到全局最优解。 这种算法不追求整体最优解,而是通过局部最优的选择逐步逼近全局最优解。贪心算法的关键在于构造合适的贪心策略,这种策略需要满足两个基本要素:贪婪选择属性和最优子…...

谷粒商城实战笔记-140-商城业务-nginx-搭建域名访问环境二(负载均衡到网关)
文章目录 一,通过域名访问商城架构设计1,为什么nginx要将请求转发给网关2,架构设计 二,配置1,nginx配置1.1 nginx.conf1.2 gulimall.conf1.3 配置原理 2,网关配置 三,记录2个问题1,网…...

【Android Studio】 创建第一个Android应用HelloWorld
文章目录 创建项目查看AndroidManifest.xml(清单)查看MainActivity.java(Activity)查看activity_main.xml(布局) 创建项目 查看AndroidManifest.xml(清单) 查看MainActivity.java(Activity&…...

C++中的错误处理机制:异常
C中的错误处理机制:异常 在软件开发中,错误处理是确保程序稳定性和健壮性的关键环节。C作为一种高级编程语言,提供了比C语言更为灵活和强大的错误处理机制——异常处理。异常处理机制允许程序在运行时检测到错误或异常情况时,能够…...

概率论原理精解【9】
文章目录 集类拓扑空间基 参考文献 集类 C是一个集类(以G的某些子集为元素的集合称为G的集类)。 A i ∈ C , ∩ i 1 n A i ∈ C , 此为有限交封闭 C 所得集类 C ∩ f A_i \in C,\cap_{i1}^nA_i \in C,此为有限交封闭C所得集类C_{\cap f} Ai∈C,∩i1n…...
-C++应用程序将onnx模型编译并转成tensorrt可执行模型)
Pytorch添加自定义算子之(11)-C++应用程序将onnx模型编译并转成tensorrt可执行模型
一、环境 参考 opencv tensorrt cuda visual studio 2019 cmake 二、CMakeLists.txt配置文件 CMAKE_MINIMUM_REQUIRED(VERSION 2.8)PROJECT(segment)set(CMAKE_CXX_FLAGS "-std=c++14 -O1")link_directories(/usr/local/cuda/lib64) # set(OpenCV_DIR "/opt/…...

C++笔记1•C++入门基础•
1.C关键字 C总计63个关键字,C语言32个关键字: 2.命名空间: 在 C/C 中,变量、函数和后面要学到的类都是大量存在的,这些变量、函数和类的名称将都存在于全局作用域中,可能会导致很多冲突。使用命名空间的目…...

Linux查看系统线程数
Linux查看系统线程数 查看线程数查看进程内的线程统计线程数 查看线程数 想要查看Linux操作系统允许的最大线程数,可以通过命令 ulimit -a返回配置项的详细说明: # core文件的最大值为100blocks core file size (blocks, -c) 0# 进程的数…...

【Python基础】Python六种标准数据类型中哪些是可变数据,哪些是不可变数据
文章目录 1.基本介绍可变数据类型不可变数据类型2.可变和不可变到底指的是什么?可变(Mutable)不可变(Immutable)总结1.基本介绍 Python 中的六种标准数据类型分为可变数据类型和不可变数据类型。以下是这些数据类型的分类: 可变数据类型 列表(List) 列表是一种有序集…...

android13去掉安全模式 删除安全模式
总纲 android13 rom 开发总纲说明 目录 1.前言 2.问题排查 3.修改方法 3.1方法1 3.2方法2 4.测试 5.彩蛋 1.前言 Android设备上的安全模式是一种诊断模式,当设备无法正常启动时,它会启动到这个模式。在这个模式下,只有系统自带的程序和服务会被运行,所有的第三方…...

LeetCode239 滑动窗口最大值
前言 题目: 239. 滑动窗口最大值 文档: 代码随想录——滑动窗口最大值 编程语言: C 解题状态: 没有思路,困难题,恐怖如斯 思路 本题的关键在于对单调队列的应用,时间复杂度 O ( n ) O(n) O(n)限…...

文件解析漏洞—IIS解析漏洞—IIS7.X
在IIS7.0和IIS7.5版本下也存在解析漏洞,在默认Fast-CGI开启状况下,在一个文件路径/xx.jpg后面加上/xx.php会将 “/xx.jpg/xx.php” 解析为 php 文件 利用条件 php.ini里的cgi.fix_pathinfo1 开启IIS7在Fast-CGI运行模式下 在 phpstudy2018 根目录创建…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
