经典七大比较排序算法 ·上
经典七大比较排序算法 ·上
- 1 选择排序
- 1.1 算法思想
- 1.2 代码实现
- 1.3 选择排序特性
- 2 冒泡排序
- 2.1 算法思想
- 2.2 代码实现
- 2.3 冒泡排序特性
- 3 堆排序
- 3.1 堆排序特性:
- 4 快速排序
- 4.1 算法思想
- 4.2 代码实现
- 4.3 快速排序特性
- 5 归并排序
- 5.1 算法思想
- 5.2 代码实现
- 5.3 归并排序特性
1 选择排序
1.1 算法思想
选择排序,每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
大致操作步骤如下:
- 第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置;
- 然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾;
- 重复第二步操作,直到全部待排序的数据元素的个数为零。
选择排序视频演示
1.2 代码实现
选择排序还是很好理解的。但这里的实现会对直接选择排序做一些小的改进。
既然直接选择排序遍历一遍可以找出最小的数据,那遍历一遍同样可以找出最大的元素。这样每遍历一次,待排序数据元素的起始位置就变成最小的了,结束位置就变成最大的了。
参考代码如下:
//n - 数据个数
void SelectSort(int* a, int n)
{int begin = 0; //待排序数据起始位置下标int end = n - 1;//待排序数据结束位置下标int minIndex = 0;//记录最小数据的下标int maxIndex = 0;//记录最大数据的下标//待排序数据大于1时进入循环while (begin < end){//假设一开始最小元素和最大元素下标都是第一个待排序数据下标minIndex = begin;maxIndex = begin;//遍历一遍for (int i = begin + 1; i <= end; ++i){//选出最小元素下标if (a[i] < a[minIndex]){minIndex = i;}//选出最大元素下标if (a[i] > a[maxIndex]){maxIndex = i;}}//将最小元素和待排序序列的起始位置交换Swap(&a[begin], &a[minIndex]);//将最大元素和待排序序列的结束位置交换Swap(&a[end], &a[maxIndex]);//缩小待排序区间,重复上述过程++begin;--end;}
}
很多老铁在敲完上面代码之后,觉得已经没有问题了。
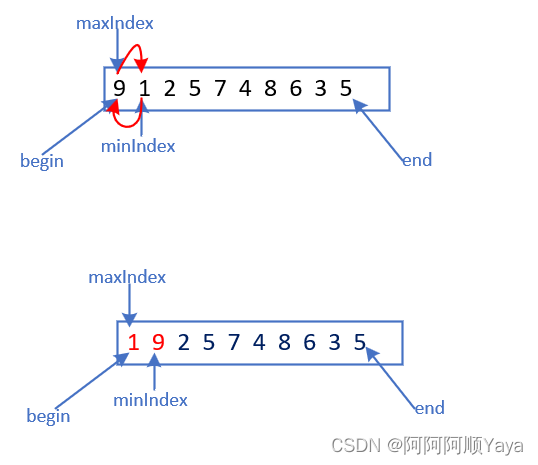
但实际上,像遇到上面情况。如果[maxIndex]指向的是[begin]中存放的内容,[minIndex]的内容先和[begin]交换之后,[maxIndex]指向的就不在是待排序序列中的最大元素了。需要做相应的修改。
Swap(&a[begin], &a[minIndex]);//如果begin和maxIndex重叠,那么修正maxInedxif (begin == maxIndex){maxIndex = minIndex;}Swap(&a[end], &a[maxIndex]);
1.3 选择排序特性
选择排序作为一种简单直观的排序算法,虽然好理解,但效率并不高。
无论是在面对什么样的排序序列,时间复杂度都是稳定的O(n2)O(n^2)O(n2)量级,实际中很少使用。
2 冒泡排序
2.1 算法思想
冒泡排序作为一种交换排序,它会重复地走访要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到不再需要交换,也就是说该数列已经排序完成。
大致操作步骤如下:
- 比较相邻的两个元素。如果第一个和第二个大元素的顺序不符合要求,就交换他们两个。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
冒泡排序视频演示
2.2 代码实现
//n - 数据个数
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){for (int j = 0; j < n - 1 - i; ++j){//排升序if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}
冒泡排序还有一种优化的方法,就是立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序,不需要再继续进行冒泡排序了。
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){int flag = 1;for (int j = 0; j < n - 1 - i; ++j){if (a[j] > a[j + 1]){flag = 0;Swap(&a[j], &a[j + 1]);}}if (1 == flag){break;}}
}
但这种改进优化在实际上对于提升性能来说并没有什么作用并不是很大。
2.3 冒泡排序特性
冒泡排序也是一种非常简单直观的排序。
在最好的情况下(序列接近有序),冒泡排序的时间复杂度是O(n)O(n)O(n)量级的;
在最坏的情况下(序列逆序),冒泡排序的时间复杂度是O(n2)O(n^2)O(n2)量级的。
3 堆排序
关于堆排序的算法思想和代码实现相关内容,可以参考阿顺的堆结构的两个应用这篇博客,里面有比较详细的介绍。这里就不在赘述了。

3.1 堆排序特性:
堆排序使用堆的结构来选数,效率就高了很多。
堆排序的平均时间复杂度是O(n∗log2n)O(n*log_2n)O(n∗log2n)量级的。
4 快速排序
4.1 算法思想
快速排序是Hoare提出的一种二叉树结构的交换排序方法。

其基本思想为:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两个子序列,其中左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后对左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
算法步骤:
- 从序列中挑出一个元素作为基准
- 排序数列,将所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆放在基准后面(相同的数可以在任一边)。在这个分区排完之后,该基准就处于数列的中间位置
- 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序
快速排序视频演示
4.2 代码实现
快速排序在发展的过程中涌现出了很多种不同的版本,但核心思想是不会变的。这里会介绍3种常见版本,以供大家参考。
//a - 待排序序列
//begin - 待排序序列起始位置
//end - 待排序序列结束位置
void QuickSort(int* a, int begin, int end)
{//序列只有一个值或没有值就不再排序if (begin >= end){return;}//对区间进行快速排序,并返回排序后的基准值位置int keyIndex = QuickPartSort(a, begin, end);//[begin, keyIndex - 1] keyIndex [keyIndex + 1, end]//左区间排序QuickSort(a, begin, keyIndex - 1);//右区间排序QuickSort(a, keyIndex + 1, end);}
上面代码就是快速排序实现的主框架,QuickPartSort函数有不同的实现方式。
其实从主框架上可以看出快速排序的递归实现和二叉树的前序遍历还是很像的。
- hoare版本
//以排升序为例
int QuickPartSort1(int* a, int begin, int end)
{int left = begin;int right = end;//取序列第1个数据做基准值int keyIndex = left;while (left < right){//右边先走,找小while (left < right && a[right] >= a[keyIndex]){--right;}//左边再走,找大while (left < right && a[left] <= a[keyIndex]){++left;}//左大右小-交换Swap(&a[left], &a[right]);}//left和right相遇,此时将基准值和相遇值交换Swap(&a[keyIndex], &a[left]);//基准值下标跟着改变keyIndex = left;return keyIndex;
}
观察hoare版本的代码发现,选择的是最左边的值做基准值。此时,却是让右边的索引先走,那能不能让左边的值先走呢?又为什么选择右边的值先走呢?
答案是左边的值先走也可以,但是处理起来细节上更复杂一些。
选择右边先走的原因是为了保证相遇位置的值,比基准值小(或者就是基准位置的值)。
右边先走的情况无非就是:
right先走,right遇到比基准值小的,right停下来,让left走,left去遇到了right。
这种情况相遇位置就是right停下来的位置,right停的位置也就是比基准值要小的位置。right先走,right没有遇到比基准值要小的值,right去遇到了left。
这种情况下,相遇位置是left上一轮停下来的位置,该位置要么是基准值的位置,要么就是比基准值小的位置。
这时,反过来想一下,如果选最左边为基准值,left先走的话,相遇位置的值就是大于基准值的,这样相遇位置的值就不能和基准值交换,这里需要做一些处理,来让基准值交换到合适的位置去,最终徒劳增加了麻烦。
所以,一般建议是:
左边做基准值,让右边先走;
右边做基准值,让左边先走。
- 挖坑版本
在面对上面hoare版本比较不好理解的左边做基准值,右边先走的问题时,挖坑法的版本能让快速排序更好理解一点点。
int QuickPartSort2(int* a, int begin, int end)
{//最左边做基准值int key = a[begin];//坑位给到基准值位置int pitIndex = begin;int left = begin;int right = end;while (left < right){//右边找小,填到左边的坑里面去。这个位置形成新的坑。while (left < right && a[right] >= key){--right;}a[pitIndex] = a[right];pitIndex = right;//左边找大,填到右边的坑里面去。这个位置形成新的坑。while (left < right && a[right] <= key){++left;}a[pitIndex] = a[left];pitIndex = left;}//坑位再填上基准值a[pitIndex] = key;return pitIndex;
}
因为坑位的存在,左边有坑,右边就走,然后填坑;右边有坑,左边就走,然后填坑。这个过程就更好理解了。但是挖坑法在算法性能上相比hoare版本并没有什么大的改进。
3. 前后指针版本
前后指针的使用和前两个版本的排序方式就有较大的区别了。
int QuickPartSort3(int* a, int begin, int end)
{//基准值选择int keyIndex = begin;int prev = begin;//前指针int cur = begin + 1;//后指针while (cur <= end){//cur位置的值小于keyIndex位置的值if (a[cur] < a[keyIndex]){++prev;Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyIndex]);keyIndex = prev;return keyIndex;
}
前后指针方法中两个指针都是从左向右的方向在走,直到cur走完整个序列。
但是在走的过程中,prev的位置+1后,如果和cur位置相等,因为指向同一个位置,就不需要交换了,代码进一步优化如下:
if (a[cur] < a[keyIndex] && ++prev != cur)
{Swap(&a[prev], &a[cur]);
}
前后指针版本不仅好理解,而且代码也很简洁,是几个版本中最推荐的了。
但是,以上方法选基准值还是存在一定问题的。
鉴于以上几个版本都选择的是最左边作为基准值,如果是排已经有序的序列的话,如下图所示:
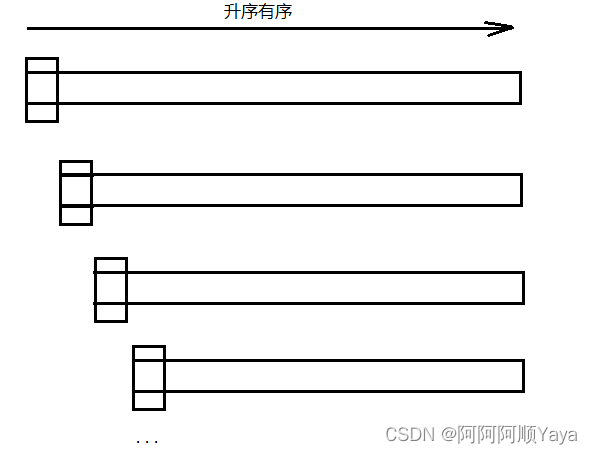
序列有多少的数据就递归多少次,很容易栈溢出。
所以,为了让每次选择基准值避免选择到序列中的最值,有的地方给出用随机数的方法选择基准值,但这里主要介绍三数取中选择基准值的方法。
所谓三数取中,不过是在序列的起止位置,中间位置,末位位置选择这三个数出来,通过比较,找到不是最大也不是最小的一个数,让这个数做基准值。
int GetMidIndex(int* a, int begin, int end)
{int mid = begin + (end - begin) / 2;if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] < a[end]){return end;}else{return begin;}}else//begin>=mid{if (a[mid] > a[end]){return mid;}else if (a[begin] < a[end]){return begin;}else{return end;}}
}
找到基准值之后,可以将基准值和序列的起始位置进行一个交换,这样就和之前排序的代码一样仍是选择序列的起始位置做基准值了。代码也不需要更多的修改了。
//三数取中优化
int mid = GetMidIndex(a, begin, end);
Swap(&a[keyIndex], &a[mid]);
因为三数取中的优化,使的每次递归左右子序列更加的二分,代码效率自然就得到了提高。
当然,我们知道递归需要是创建销毁和销毁栈帧的(具体参考阿顺的这篇博文你也能看懂的的函数栈帧创建与销毁)
因为快速排序的递归和二叉树前序递归很像,如果快速递归的划分接近二分的话,就会像满二叉树的遍历一样,最后一层的数量(2h−12^{h-1}2h−1)会是整棵树数量(2h−12^h-12h−1)的一半,也就是快速排序最后一层的递归次数是整个过程递归次数的一半。在面对小数据量时,还要递归这么多次,进行栈帧的开销,确实会影响到程序的效率。
所以,可以对小区间进行优化:当递归划分小区间,区间比较小的时候,就不再递归划分去排序这个小区间。而是可以考虑直接用其它排序对小区间进行处理。
这里就给出对小区间元素小于10时的插入排序处理。
if (end - begin > 10)
{//int keyIndex = PartSort1(a, begin, end);//int keyIndex = PartSort2(a, begin, end);int keyIndex = QuickPartSort3(a, begin, end);QuickSort(a, begin, keyIndex - 1);QuickSort(a, keyIndex + 1, end);
}
else
{InsertSort(a + begin, end - begin + 1);
}

通过计算可以得出,以上代码在采用小区间优化后,函数调用次数可以减少80%80\%80%左右,这种提升还是很明显的。
以上都是对快速排序的递归版本的介绍。但是递归有一个死穴就是递归太深,栈溢出,程序会崩溃。所以,也要能够对快速排序进行非递归的实现。
可以借助栈数据结构或者队列数据结构进行非递归实现。这里就选择栈数据结构来进行实现。借助栈来实现的运行逻辑是可以和递归实现的递归逻辑达成一致的。
因为是C语言实现,所以对于栈数据结构的需要可以参考阿顺的这篇博文顺序表实现栈(C语言)
void QuickSortNonR(int* a, int begin, int end)
{Sk stack;StackInit(&stack);StackPush(&stack, end);StackPush(&stack, begin);while (!StackEmpty(&stack)){int left = StackTop(&stack);StackPop(&stack);int right = StackTop(&stack);StackPop(&stack);int keyIndex = QuickPartSort3(a, left, right);// [left, keyIndex-1] keyIndex [keyIndex+1, right]if (keyIndex + 1 < right){StackPush(&stack, right);StackPush(&stack, keyIndex + 1);}if (left < keyIndex - 1){StackPush(&stack, keyIndex - 1);StackPush(&stack, left);}}StackDestroy(&stack);
}

代码结合画图就很容易理解快速排序的非递归了。
4.3 快速排序特性
快速排序,一听到这个名字你就知道它存在的意义l。而且快速排序整体的综合性能和使用场景都是比较好的,所以也才敢叫快速排序。
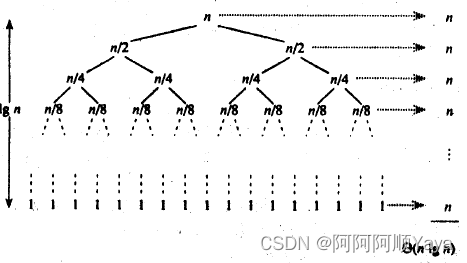
快速排序的一次划分算法从两头交替搜索,直到left和right重合,因此其时间复杂度是O(n)O(n)O(n);而整个快速排序算法的时间复杂度与划分的趟数有关。
理想的情况是,每次划分所选择的中间数恰好将当前序列几乎等分,经过log2nlog_2nlog2n趟划分,便可得到长度为1的子表。这样,整个算法的时间复杂度为O(n∗log2n)O(n*log_2n)O(n∗log2n)。
最坏的情况是,每次所选的中间数是当前序列中的最大或最小元素,这使得每次划分所得的子表中一个为空表,另一子表的长度为原表的长度-1。这样,长度为n的数据表的快速排序需要经过n趟划分,使得整个排序算法的时间复杂度为O(n2)O(n2)O(n2)。
从空间性能上看,尽管快速排序只需要一个元素的辅助空间,但快速排序需要一个栈空间来实现递归。最好的情况下,即快速排序的每一趟排序都将元素序列均匀地分割成长度相近的两个子表,所需栈的最大深度为log2(n+1)log_2{(n+1)}log2(n+1);但最坏的情况下,栈的最大深度为n。
5 归并排序
5.1 算法思想
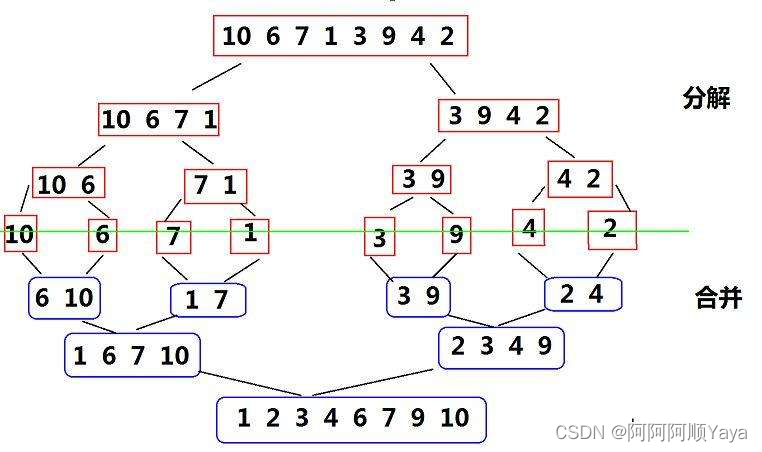
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序。若将两个有序表合并成一个有序表,称为二路归并。
算法步骤:
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别指向两个已经排序序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤 3 直到某一指针到达序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾。
归并排序视频演示
5.2 代码实现
作为一种典型的分而治之思想的算法应用,归并排序的实现有两种方法:
- 自上而下的递归;
//n - 数据个数
void MergeSort(int* a, int n)
{//开辟归并空间int* tmp = (int*)malloc(n * sizeof(int));assert(tmp != NULL);//归并排序_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
void _MergeSort(int* a, int begin, int end, int* tmp)
{//递归区间不足1个数据就不再递归//因为1个数据即有序if (begin >= end){return;}int mid = begin + (end - begin) / 2;// [begin, mid][mid+1, end] 分治递归,让子区间有序//左区间递归_MergeSort(a, begin, mid, tmp);//又去见递归_MergeSort(a, mid+1, end, tmp);//归并过程int begin1 = begin;int end1 = mid;int begin2 = mid + 1;int end2 = end;int i = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}//把归并数据拷贝回原数组memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
- 自下而上的迭代。

所谓自下而上的迭代,不过是最开始从1个和1个开始归并(因为1个数据即有序)。
之后每次归并数据都扩2倍,直到最后一组的数据已经大于等于整个序列的数据为止就完成归并了。可以用循环来解决。
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(n * sizeof(int));assert(tmp != NULL);//最开始,一组只有一个数据int gap = 1;//一组的数据要小于序列长度while (gap < n){for (int i = 0; i < n; i += 2 * gap){//[i,i+gap-1]和[i+gap, i+2*gap-1]区间的数据进行归并int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}//一趟归并结束进行拷贝memcpy(a, tmp, n * sizeof(int));//一组数据扩2倍gap *= 2;}free(tmp);
}
但是上面代码有一个致命的bug就是,只能适用于2n2^n2n个数据的归并。否则就存在越界的错误。
所以需要对归并区间进行界线的判断和修正。
因为begin1=i不会越界,而end1 begin2 end2都可能越界。
所以存在三种情况下的修正:
//修正边界
if (end1 >= n)
{end1 = n - 1;begin2 = n;end2 = n - 1;
}
else if (begin2 >= n)
{begin2 = n;end2 = n - 1;
}
else if (end2 >= n)
{end2 = n - 1;
}
上述是修正的一种方法。还可以采用更省事的策略:在遇到越界的区间时,就不再归并了。
if (end1 >= n || begin1 >= n)
{break;
}
else if (end2 >= n)
{end2 = n - 1;
}
但这种方法,需要每归并一次,就拷贝一次,而不是等到一趟归并完在拷贝。memcpy函数应该放在for循环之内。
5.3 归并排序特性
归并排序的时间复杂度是稳定的O(n∗log2n)O(n*log_2n)O(n∗log2n),而因为要开辟额外的归并数组,所以空间复杂度是O(n)O(n)O(n)。
归并排序速度仅次于快速排序,一般用于对总体无序,但是各子项相对有序的数列排序。
归并排序的比较次数小于快速排序的比较次数,移动次数一般多于快速排序的移动次数。
虽然归并排序比较占用内存,但却是一种效率高且稳定的算法。
相关文章:

经典七大比较排序算法 ·上
经典七大比较排序算法 上1 选择排序1.1 算法思想1.2 代码实现1.3 选择排序特性2 冒泡排序2.1 算法思想2.2 代码实现2.3 冒泡排序特性3 堆排序3.1 堆排序特性:4 快速排序4.1 算法思想4.2 代码实现4.3 快速排序特性5 归并排序5.1 算法思想5.2 代码实现5.3 归并排序特性…...

【网络安全工程师】从零基础到进阶,看这一篇就够了
学前感言 1.这是一条需要坚持的道路,如果你只有三分钟的热情那么可以放弃往下看了。 2.多练多想,不要离开了教程什么都不会,最好看完教程自己独立完成技术方面的开发。 3.有问题多google,baidu…我们往往都遇不到好心的大神,谁…...
素描-基础
# 如何练习排线第一次摸板子需要来回的排线,两点然后画一条线贯穿两点画直的去练 练线的定位叫做穿针引线法或者两点一线法 练完竖线练横线 按照这样去练顺畅 直线曲线的画法 直线可以按住shift键 练习勾线稿 把线稿打开降低透明度去勾线尽量一笔的去练不要压…...
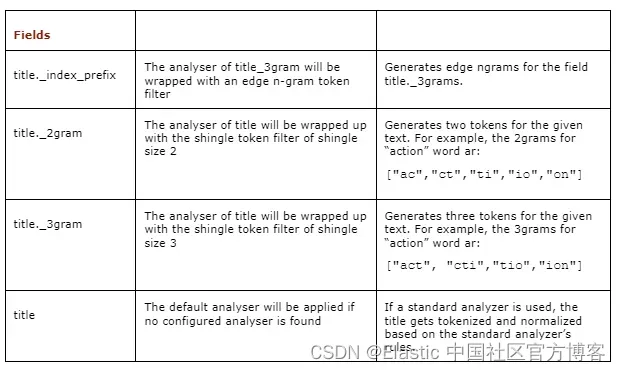
Elasticsearch:高级数据类型介绍
在我之前的文章 “Elasticsearch:一些有趣的数据类型”,我已经介绍了一下很有趣的数据类型。在今天的文章中,我再进一步介绍一下高级的数据类型,虽然这里的数据类型可能和之前的一些数据类型有所重复。即便如此,我希望…...

Golang每日一练(leetDay0012)
目录 34. 查找元素首末位置 Find-first-and-last-position-of-element-in-sorted-array 🌟🌟 35. 搜索插入位置 Search Insert Position 🌟 36. 有效的数独 Valid Sudoku 🌟🌟 🌟 每日一练刷题专栏 …...

Web前端:6种基本的前端编程语言
如果你想在前端web开发方面开始职业生涯,学习JavaScript是必须的。它是最受欢迎的编程语言,它功能广泛,功能强大。但JavaScript并不是你唯一需要知道的语言。HTML和CSS对于前端开发至关重要。他们将帮助你开发用户友好的网站和应用程序。什么…...
九【springboot】
Springboot一 Spring Boot是什么二 SpringBoot的特点1.独立运行的spring项目三 配置开发环境四 配置开发环境五 创建 Spring Boot 项目1.在 IntelliJ IDEA 欢迎页面左侧选择 Project ,然后在右侧选择 New Project,如下图2.在新建工程界面左侧,…...

《程序员成长历程的四个阶段》
阶段一:不知道自己不知道(Unconscious incompetence) 大学期间,我和老师做过一些小项目,自认为自己很牛,当时还去过一些公司面试做兼职,但是就是不知道为什么没有回复。那个时期的我,压根不知道自己不知道&…...

【SpringBoot】Spring data JPA的多数据源实现
一、主流的多数据源支持方式 将数据源对象作为参数,传递到调用方法内部,这种方式增加额外的编码。将Repository操作接口分包存放,Spring扫描不同的包,自动注入不同的数据源。这种方式实现简单,也是一种“约定大于配置…...

uni-app基础知识介绍
uni-app的基础知识介绍 1、在第一次将代码运行在微信开发者工具的时候,应该进行如下的配置: (1)将微信开发者工具路径进行配置; [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lbyk5Jw2-16790251840…...
Word2010(详细布局解释)
目录一、界面介绍二、选项卡1、文件选项卡(保存、打开、新建、打印、保存并发送、选项)2、开始选项卡(剪贴板、字体、段落、样式、编辑)3、插入选项卡(页、表格、插图、链接、页眉页脚、文本、符号)4、页面…...
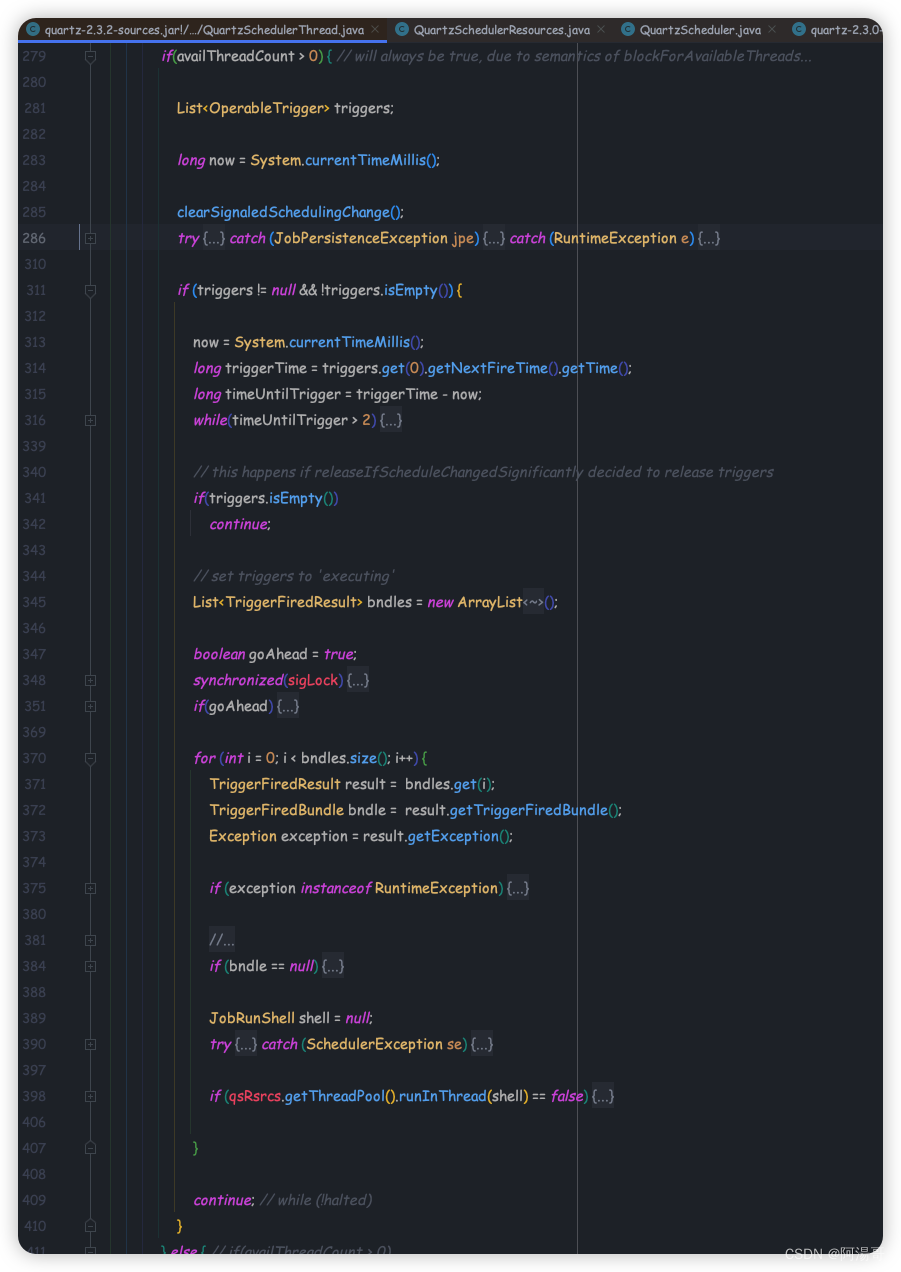
Spring如何实现Quartz的自动配置
Spring如何实现Quartz的自动配置1. 开启Quartz自动配置2. Quartz自动配置的实现过程2.1 核心类图2.2 核心方法3. 任务调度执行3.1 大致流程3.2 调整线程池的大小如果想在应用中使用Quartz任务调度功能,可以通过Spring Boot实现Quartz的自动配置。以下介绍如何开启Qu…...

计算机组成原理——作业四
一. 单选题(共11题,33分) 1. (单选题, 3分)四片74181 ALU和一片74182 CLA器件相配合,具有如下进位传递功能:________。 A. 行波进位B. 组内先行进位,组间行波进位C. 组内先行进位,组间先行进位D. 组内行波进位,组间先行进位 我的答案: C 3…...
)
2023前端面试题(经典面试题)
经典面试题Vue2.0 和 Vue3.0 有什么区别?vue中计算属性和watch以及methods的区别?单页面应用和多页面应用区别及优缺点?说说 Vue 中 CSS scoped 的原理?谈谈对Vue中双向绑定的理解?为什么vue2和vue3语法不可以混用&…...

【Linux内网穿透】使用SFTP工具快速实现内网穿透
文章目录内网穿透简介1. 查看地址2.局域网测试连接3.创建tcp隧道3.1. 安装cpolar4.远程访问5.固定TCP地址内网穿透简介 是一种通过公网将内网服务暴露出来的技术,可以使得内网服务可以被外网访问。以下是内网穿透的一些应用: 远程控制:通过内…...

SQL语句性能分析
1. 数据库服务器的优化步骤 当我们遇到数据库调优问题的时候,该如何思考呢?这里把思考的流程整理成下面这张图。 整个流程划分成了 观察(Show status) 和 行动(Action) 两个部分。字母 S 的部分代表观察&…...

【K3s】第28篇 详解 k3s-killall.sh 脚本
目录 k3s-killall.sh 脚本 k3s-killall.sh 脚本 为了在升级期间实现高可用性,当 K3s 服务停止时,K3s 容器会继续运行。 要停止所有的 K3s 容器并重置容器的状态,可以使用k3s-killall.sh脚本。 killall 脚本清理容器、K3s 目录和网络组件&a…...

生成时序异常样本-学习记录-未完待续
1.GAN&VAE|时间序列生成及异常注入那些事儿:主要讲了数据增广,用GAN、WGAN、DCGAN、VAE,有给几个代码的github的链接,非常有用 2.时序异常检测综述,写的非常好 3.自编码器原理讲解,后面还附…...
自定义类型的超详细讲解ᵎᵎ了解结构体和位段这一篇文章就够了ᵎ
目录 1.结构体的声明 1.1基础知识 1.2结构体的声明 1.3结构体的特殊声明 1.4结构体的自引用 1.5结构体变量的定义和初始化 1.6结构体内存对齐 那对齐这么浪费空间,为什么要对齐 1.7修改默认对齐数 1.8结构体传参 2.位段 2.1什么是位段 2.2位段的内存分配…...
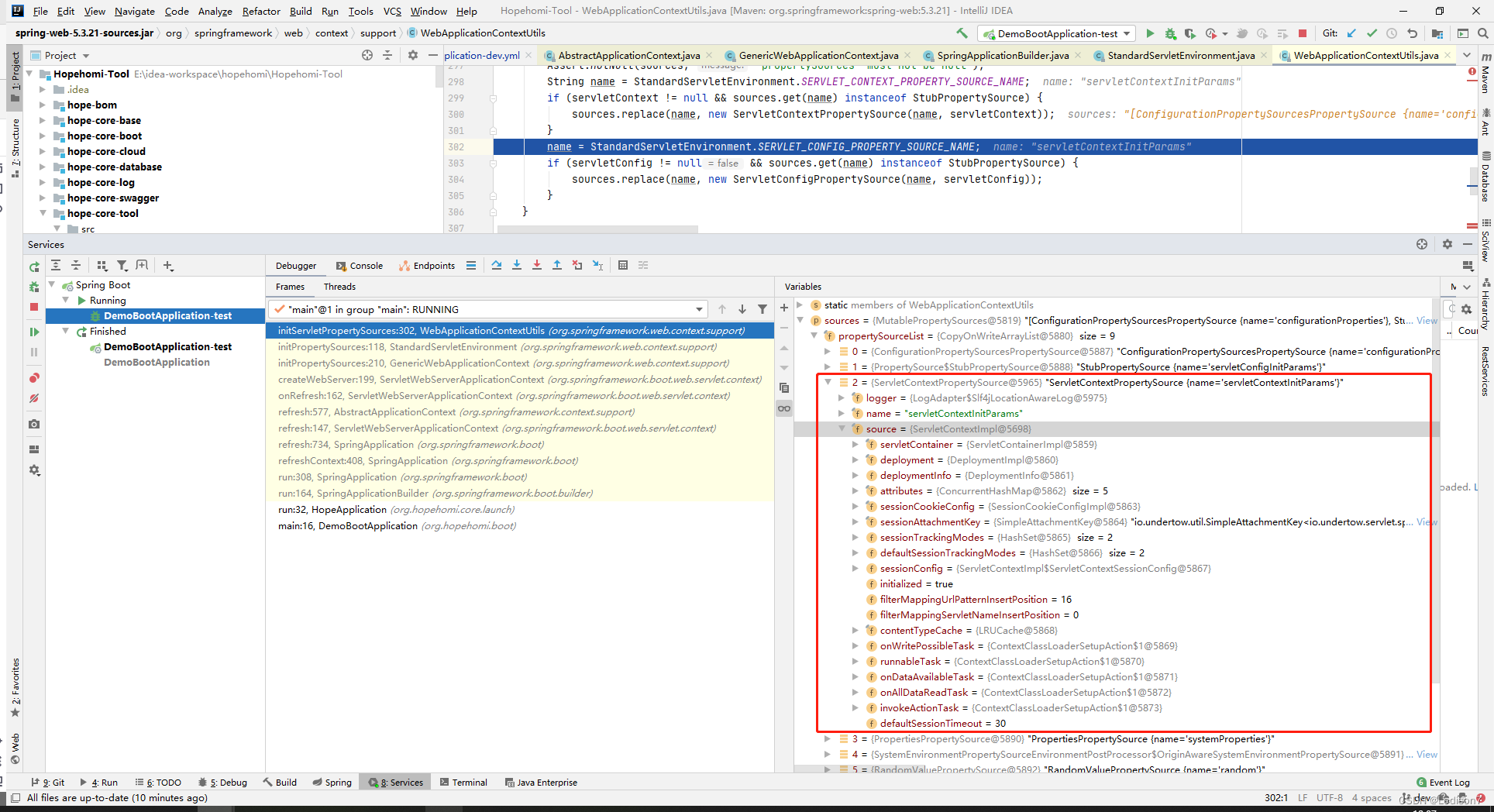
【五】springboot启动源码 - onRefresh
onRefresh 源码解析 Initialize other special beans in specific context subclasses. 核心是创建一个web服务容器(并未在这个方法启动) createWebServer第182行,获取ServletWebServerFactory的具体实现 getWebServerFactory方法ÿ…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
