算法【滑动窗口】
滑动窗口指的是维持左、右边界都不回退的一段范围,来求解很多子数组(串)的相关问题。
滑动窗口的关键是找到范围和答案指标之间的单调性关系(类似贪心)。
滑动过程:滑动窗口可以用简单变量或者结构来维护信息。
求解大流程:求子数组在每个位置开头或结尾情况下的答案(开头还是结尾在于个人习惯)。
下面通过几个题目加深理解。
题目一
测试链接:https://leetcode.cn/problems/minimum-size-subarray-sum/
分析:如果判断左右边界不回退是应用滑动窗口的关键。设滑动窗口代表以right为结尾的满足条件的最短子数组。假设存在一个满足条件的最短子数组,那么,将left回退,也就是左移也一定会满足条件,而我们是要求最短的子数组,所以确定了right的情况下,left是不会回退的。然后right继续右移,寻找更多情况。直到找到满足条件的子数组,再判断left是否需要右移。遍历数组即可找到最短子数组的长度。代码如下。
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int ans = 100005;int left = 0, right = 0;int sum = 0;for(;right < nums.size();++right){sum += nums[right];if(sum >= target){while (sum - nums[left] >= target){sum -= nums[left++];}ans = ans < (right - left + 1) ? ans : (right - left + 1);}}return ans == 100005 ? 0 : ans;}
};其中,将ans初始化为100005是因为nums数组最长为100000,只要比这个数大就行。
题目二
测试链接:https://leetcode.cn/problems/longest-substring-without-repeating-characters/
分析:设滑动窗口为以right为结尾的符合条件的最长子串。可以通过一个数组记录每个符号最晚出现的下标。当right来到一个字符的时候,把left置为right最晚出现位置下标加1和left的最大值,这时候ans和right-left+1取最大值,然后更新right处字符最晚出现的下标。遍历数组即可得到最长符合条件的子串长度。代码如下。
class Solution {
public:int lengthOfLongestSubstring(string s) {vector<int> position;int ans = 0;position.assign(256, -1);for(int left = 0, right = 0;right < s.size();++right){left = left > (position[s[right]] + 1) ? left : (position[s[right]] + 1);ans = ans > (right - left + 1) ? ans : (right - left + 1);position[s[right]] = right;}return ans;}
};其中,position存储各字符最晚出现下标,初始化为-1,方便对一个未出现过的字符更新left值时,将left更新为0。
题目三
测试链接:https://leetcode.cn/problems/minimum-window-substring/
分析:设滑动窗口为以right为结尾的子串。可以通过一个数组记录,每个字符串t中的每种字符的需要被覆盖的个数,同时用一个变量记录总的需要被覆盖个数。当覆盖个数达到要求时,开始调整left。调整后计算ans和right-left+1的最小值。遍历数组即可求得符合条件的最小子串的长度。代码如下。
class Solution {
public:string minWindow(string s, string t) {if(s.size() < t.size()){return "";}vector<int> cnt;int ans = 100005;int l;int count = -t.size();cnt.assign(256, 0);for(int i = 0;i < t.size();++i){--cnt[t[i]];}for(int left = 0, right = 0;right < s.size();++right){if(cnt[s[right]] < 0){count++;}cnt[s[right]]++;if(count >= 0){while (cnt[s[left]] - 1 >= 0){cnt[s[left++]]--;}if((right - left + 1) < ans){ans = (right - left + 1);l = left;}}}return ans == 100005 ? "" : s.substr(l, ans);}
};其中,ans设为100005的原因之前说过,cnt数组用来记录每种字符需要被覆盖的次数,当大于等于0时代表对此种字符覆盖完毕,count是总的用来记录覆盖完成与否。
题目四
测试链接:https://leetcode.cn/problems/gas-station/
分析:设滑动窗口为以begin为开头的能否走完全程。从begin开始,只要总油量小于0,begin就前移。直到走下去,发现距离等于数组长度,就可以返回begin。如果遍历完数组没有返回begin,则返回-1。代码如下。
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int length = gas.size();for(int begin = 0, end = 0, soil = 0, distance = 0; begin < length;++begin){while (soil >= 0){if(distance == length){return begin;}end = (begin + distance++) % length;soil += (gas[end] - cost[end]);}soil -= (gas[begin] - cost[begin]);distance--;}return -1;}
};题目五
测试链接:https://leetcode.cn/problems/replace-the-substring-for-balanced-string/
分析:设滑动窗口为以left为开头,最少需要多长的自由变换的区间,可以符合条件。就是说除了自由变换区间中的字符,其他字符不动,只变换自由变换区间中的字符就可以使这个字符串满足条件。确定下left和right之后,更新ans,右移left,而right并不需要回退。这是因为如果left到right区间是自由变换区间,那么left到right+1区间也是自由变换区间。同理,如果left到right-1区间不是自由变换区间,则left+1到right-1区间也不是自由变换区间。所以当left右移时,right并不需要回退。代码如下。
class Solution
{
public:int cnt[4] = {0};bool ok(int num){for (int i = 0; i < 4; ++i){if (cnt[i] > num){return false;}}return true;}int get_index(char ch){switch (ch){case 'Q':return 0;case 'W':return 1;case 'E':return 2;case 'R':return 3;}return -1;}int balancedString(string s){int length = s.size();int num = (length >> 2);for (int i = 0; i < length; ++i){++cnt[get_index(s[i])];}if (cnt[0] == num && cnt[1] == num && cnt[2] == num && cnt[3] == num){return 0;}int ans = length;for (int left = 0, right = 0; left < length; ++left){while (!ok(num) && right < length){--cnt[get_index(s[right++])];}if (ok(num)){ans = ans < (right - left) ? ans : (right - left);}++cnt[get_index(s[left])];}return ans;}
};其中,cnt数组是用来记录除滑动窗口外每种字符的个数,ok方法判断当前滑动窗口是否可以作为自由变换区间。注意,代码中区间为左闭右开,即[left, right)。
题目六
测试链接:https://leetcode.cn/problems/subarrays-with-k-different-integers/
分析:这个题可以将其分解出来,我们可以写一个f方法用来计算子数组中小于等于k种整数的子数组个数。而要求题目的解只需要f(k)-f(k-1)即可。而分解出来的f方法则可以分析出单调性使用滑动窗口求解。代码如下。
class Solution {
public:vector<int> cnt;int f(int num, vector<int>& nums){cnt.assign(20001, 0);int ans = 0;int count = 0;for(int left = 0, right = 0;right < nums.size();++right){if(cnt[nums[right]]++ == 0){++count;}while (count > num){if(--cnt[nums[left++]] == 0){--count;}}ans += (right - left + 1);}return ans;}int subarraysWithKDistinct(vector<int>& nums, int k) {return f(k, nums) - f(k-1, nums);}
};其中,count为种类数。
题目七
测试链接:https://leetcode.cn/problems/longest-substring-with-at-least-k-repeating-characters/
分析:此题也是一样的,如果直接求解,单调性很难分析出来。我们可以将其分解为子串中只能有i种字符,每种字符必须出现的次数必须大于等于k。只需将i从1到26遍历一次,即可找到符合条件的最大子串长度。代码如下。
class Solution {
public:vector<int> cnt;int longestSubstring(string s, int k) {int ans = 0;int length = s.size();for(int i = 1;i <= 26;++i){cnt.assign(26, 0);for(int left = 0, right = 0, kind = 0, match = 0;right < length;++right){if(cnt[s[right] - 'a'] == 0){++kind;}if(cnt[s[right] - 'a'] == k-1){++match;}++cnt[s[right] - 'a'];while (kind > i){--cnt[s[left] - 'a'];if(cnt[s[left] - 'a'] == k-1){--match;}if(cnt[s[left] - 'a'] == 0){--kind;}++left;}if(match == i){ans = ans > (right - left + 1) ? ans : (right - left + 1);}}}return ans;}
};其中,kind为[left, right]区间字符种类数,match为区间中大于等于k的字符种类数。
相关文章:

算法【滑动窗口】
滑动窗口指的是维持左、右边界都不回退的一段范围,来求解很多子数组(串)的相关问题。 滑动窗口的关键是找到范围和答案指标之间的单调性关系(类似贪心)。 滑动过程:滑动窗口可以用简单变量或者结构来维护…...

【RISC-V设计-06】- RISC-V处理器设计K0A之ALU
【RISC-V设计-06】- RISC-V处理器设计K0A之ALU 文章目录 【RISC-V设计-06】- RISC-V处理器设计K0A之ALU1.简介2.顶层设计3.内部结构4.端口说明5.操作码说明6.设计代码7.总结 1.简介 算术逻辑单元(Arithmetic Logic Unit,简称 ALU)是计算机中…...
MyIP:强大且简单好用!
在这个数字化的时代,IP地址就像是我们的网络身份证。各位在日常的工作中,肯定会会遇到需要和 IP 地址相关的需求。 今天和大家聊一聊一个非常好用的开源 IP 工具项目 - MyIP。 简介 MyIP一个开源IP工具箱,提供了一系列的网络检测工具&…...

Redis作为缓存,如何与MySql的数据进行同步?
允许延时一致的业务 概念 采用异步通知使用MQ作为中间件,更新数据之后通知缓存删除利用canal中间件,不需要修改业务代码,伪装成Mysql的一个从节点,canal通过读取binlog数据更新缓存 强一致性业务 概念 采用Redission提供的读写锁…...

Android 通知栏推送功能
Android 通知栏推送功能 Android 通知栏推送功能 让消息在用户的通知栏上显示,并且点击后跳转到指定的页面 MainActivity.Java import android.app.Notification; import android.app.NotificationChannel; import android.app.NotificationManager; import andro…...

【LVS】防火墙mark标记解决调度问题
实验环境是在之前部署DR模式集群的基础上做的,参考如下 部署DR模式集群 以http和https为例,当我们在webserver中同时开放80和443端口,那么默认控制是分开轮询的,就会出现了一个轮询错乱的问题: 当第一次访问80被轮询…...

算法笔记|Day20回溯算法II
算法笔记|Day20回溯算法II ☆☆☆☆☆leetcode 39. 组合总和题目分析代码 ☆☆☆☆☆leetcode 40.组合总和II题目分析代码 ☆☆☆☆☆leetcode 131.分割回文串题目分析代码 ☆☆☆☆☆leetcode 39. 组合总和 题目链接:leetcode 39. 组合总和 题目分析 本题采用回…...

Oracle认证1Z0-071线上考试注意事项
目录 一、前言二、回顾过往战绩第一次 裸考🐒第二次 背题库硬考!🐒第三次 软件卡住,寄!🙈第四次 汇总纠错,通过!🌚 三、考试流程四、考试注意事项1. 是否需要科学上网2. …...

【C++ 面试 - 基础题】每日 3 题(八)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/fYaBd 📚专栏简介:在这个专栏中,我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏&…...
影响LabVIEW工作效率的因素有哪些
影响LabVIEW工作效率的因素可以分为多个方面,涵盖硬件、软件、开发环境和编程习惯等。以下是一些常见的影响因素: 1. 硬件因素 处理器性能:处理器的速度和核心数量对LabVIEW程序的执行效率有很大影响。 内存大小:足够的内存可以保…...
)
linux 裸机.之SPV5210,dnw,usb,sdk,fastboot刷机(一)
linux 裸机.之SPV5210,dnw,usb,sdk,fastboot刷机(一)...
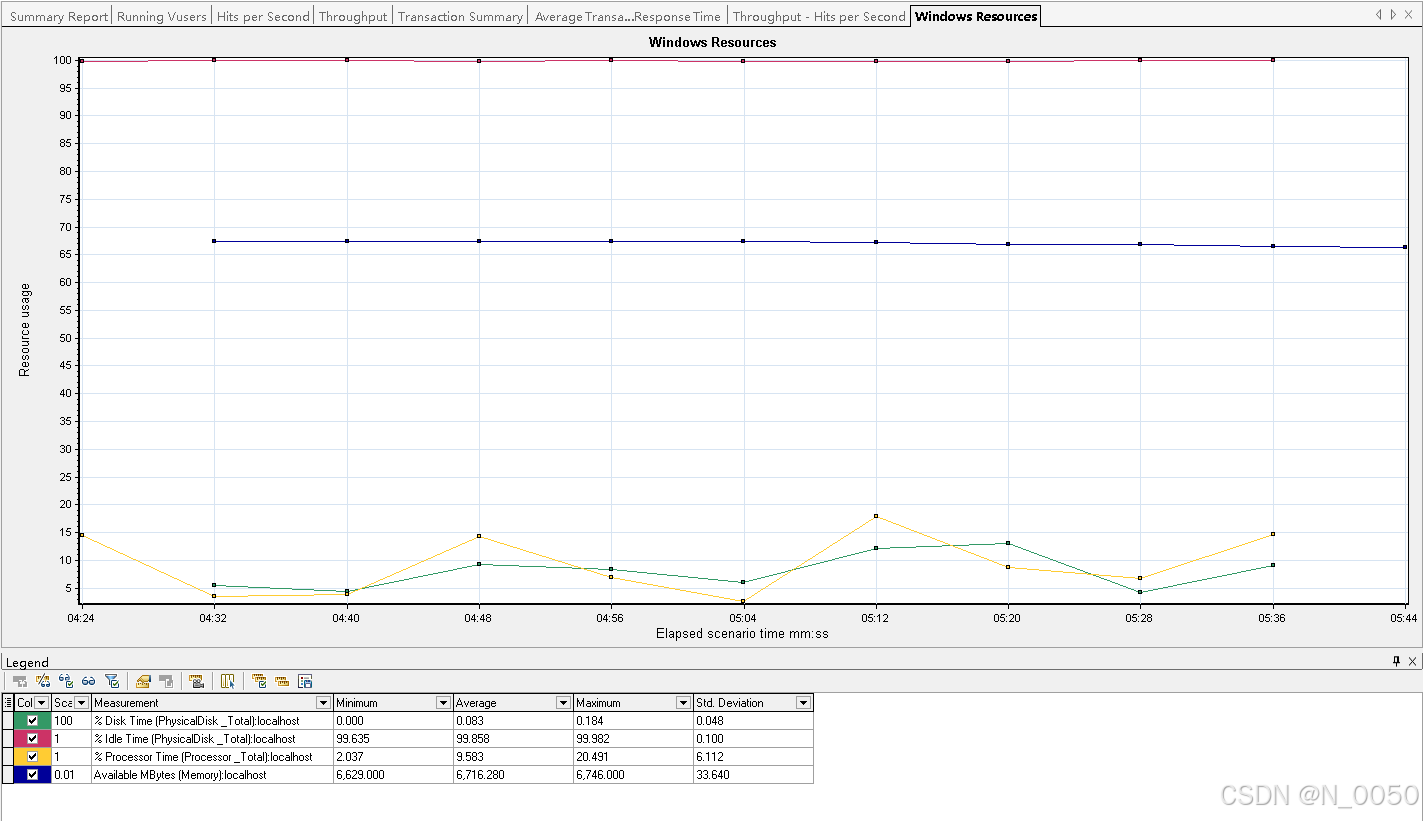
性能测试工具LoadRunner
前言👀~ 上一章我们介绍了性能测试的一些基本概念,重要的是性能测试的各项指标,今天我们使用性能测试工具LoadRunner简单的完成一次性能测试 性能测试Load Runner LoadRunner是什么? LoadRunner安装 LoadRunner脚本录制 1.录…...

智能归来:深入探索人工智能回归模型的奥秘
人工智能之回归模型 1. 回归模型的数学基础1.1 回归分析的基本原理1.1.1 目标变量与预测变量的关系1.1.2 线性回归模型 1.2 矩阵形式的回归模型1.2.1 回归方程的矩阵表示1.2.2 矩阵运算的基本性质及其在回归分析中的应用 1.3 总结 2. 最小二乘法 (Ordinary Least Squares, OLS)…...
 和 对象.init() 的共同点和异同点)
swift 中,对象() 和 对象.init() 的共同点和异同点
在阅读同事的代码时,不同人对对象的初始化方式是不一样的,例如存在一个对象AController, 有些人创建的方式如下: let controller AController()也有人创建的方式如下: let controller AController.init()下面来说明一下&#…...

Google安装JSON-handle扩展
JSON-hande下载地址: JSON-Handle 官网 - 打开json格式文件的浏览编辑器 1. 重命名扩展文件(crx)后缀 为 zip。 2. 解压zip成文件夹,保存到指定目录。 3. Google浏览器地址栏输入 “chrome://extensions/”回车。然后开启 开发者模式。 4. 点击“加载…...

剖析算法内部结构----------贪心算法
什么是贪心算法? 贪心算法(Greedy Algorithm)是一种在问题求解过程中,每一步都采取当前状态下最优(即最有利)的选择,从而希望导致最终的全局最优解的算法策略。 贪心算法的核心思想是做选择时&…...

uni-app开发微信小程序注意事项,不要用element-ui
前端扩展组件千万不要用element-ui,开发的时候不报错,发布的时候会报错无法发布。 可以用vant weapp【注意是weapp】 iView weapp 附上hbuilder官方文档 组件的概念 | uni-app官网 (dcloud.net.cn)...
)
Hibernate的检索策略(lazy、fetch、batch-size)
Hibernate的检索策略包括立即检索和延迟检索,可以在配置文件中通过对lazy、fetch、batch-size属性的设置来进行控制。一对多、多对多、多对一和一对一关系下的不同检索策略将影响对数据库访问的效率。 检索策略 立即检索,立即加载检索方法指定的对象延…...
第四十六天 | 110. 字符串接龙、105. 有向图的完全可达性、106. 岛屿的周长)
算法训练(leetcode)第四十六天 | 110. 字符串接龙、105. 有向图的完全可达性、106. 岛屿的周长
刷题记录 *110. 字符串接龙105. 有向图的完全可达性邻接矩阵邻接表 106. 岛屿的周长深搜简化代码 *110. 字符串接龙 题目地址 使用广搜。 本题相当于求最短路径,因此使用广搜。如何应用广搜是一个难点,因为题目给的是字符串而非图的表示(邻…...
)
自定义Mybatis-Plus分布式ID生成器(解决ID长度超过JavaScript整数安全范围问题)
自定义MyBatis-Plus分布式ID生成器(解决ID长度超过JavaScript整数安全范围问题) 版本 MyBatis-Plus 3.4.1 问题 MyBatis-Plus 默认生成的是 64bit 长整型,而 JS 的 Number 类型精度最高只有 53bit,如果以 Long 类型 ID 和前端…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
