动态规划之——背包DP(完结篇)
文章目录
- 概要说明
- 分组背包
- 模板例题1
- 思路
- code
- 模板例题2
- 思路
- code
- 有依赖的背包问题
- 模板例题
- 思路
- code
- 背包问题求方案数
- 模板例题
- 思路
- code
- 背包问题求具体方案
- 模板例题
- 思路
- code
概要说明
本文讲分组背包、有依赖的背包、 背包问题求方案数以及背包问题求具体方案
入门篇(01背包和完全背包问题):传送门
进阶篇(多重、混合、二维费用背包):传送门
分组背包
模板例题1
acwing-分组背包问题
思路
分组背包也是01背包的一个变形,01背包中我们有n个物品,在这题中我们有n个组别,每个组别有k个物品
因此我们可以对每个组别都进行01背包,在当前组别选出最优解的情况下在进行下一轮组别的01背包
它的状态转移方程和01背包一样,在01背包的基础上改动一点点即可
它的时间复杂度在 O ( n 3 ) O(n^3) O(n3)
code
const int N=1e3+5;
int cnt[N],f[N],w[N][N],v[N][N];
void solve(){int W,n,t=1;cin >> n >> W;for(int i=1;i<=n;++i){cin >> cnt[i];for(int j=1;j<=cnt[i];++j){cin >> w[i][j] >> v[i][j];} }for(int i=1;i<=n;++i) for(int j=W;j>=0;--j)for(int k=1;k<=cnt[i];++k){if(j>=w[i][k]){f[j]=max(f[j],f[j-w[i][k]]+v[i][k]);}}cout << f[W];return ;
}
模板例题2
通天之分组背包
思路
这题在模板例题1的基础上稍微变动了一点点,它没有给你确切的组数
因此我们需要先找出最大的组数,并另开一个数组存当前组数的下标
剩下的和模板例题1差不多,代码如下:
code
const int N=1e3+5;
int cnt[N],f[N],w[N],v[N],g[N][N];//g数组中,行存的是组别,列存的是个数,它的取值存的是下标
void solve(){int W,n,t=0;cin >> W >> n;for(int i=1;i<=n;++i){int x;cin >> w[i] >> v[i] >> x;cnt[x]++;t=max(t,x);g[x][cnt[x]]=i;}for(int i=1;i<=t;++i) for(int j=W;j>=0;--j)for(int k=1;k<=cnt[i];++k){int st=g[i][k];//取出当前组别的下标if(j>=w[st]){f[j]=max(f[j],f[j-w[st]]+v[st]);}}cout << f[W];return ;
}
有依赖的背包问题
模板例题
有依赖的背包问题
思路
首先我们明确一点:想要取出子节点必须取出父节点
那么想要价值尽可能大,我们必须倒着遍历这颗树
遍历树最基本的算法是什么呢?
很显然,我们很快就能想到dfs回溯的思想,先来看这张图:

先看左边这条线1-2-4,我们将这颗树的节点分开来看,4的父节点为2,2的父节点1
那么我们想取出4的价值,首先必须取出2的价值,我们想取出2的价值,首先必须取出1的价值
我们倒着遍历树,当我们遍历到4时,发现4没有子节点,这时我们就回溯到前一个状态2
在回溯之前我们将4的价值存入到一个数组中,这时我们考虑状态2,它有2种选择,选或者不选
这时候它的状态转移方程和01背包是一样的
注意:在选状态4物品之前需要减去状态2的重量,因为状态2必须先选,才能选状态4
接着我们将选完的状态回溯到前一个状态1,同理,我们在选物品之前需要先减去状态1的重量
然后它也是有2种选择,选或者不选
对于其他线路也是同理,最终都会回溯到状态1,那么我们只需要从状态1开始进行dfs,遍历到树的叶节点时开始回溯即可
讲完思路,接着讲一下如何用代码实现出来
首先我们需要标记根节点的位置,用vector建树,将子节点存入父节点中
开一个二维数组,行代表节点,列代表重量w,所存的值为价值v
将根节点进行dfs,将当前 f [ x ] [ w − W ] 都标记为 v , x 代表节点, w 代表重量, W 为背包容量, v 为价值 f[x][w-W]都标记为v,x代表节点,w代表重量,W为背包容量,v为价值 f[x][w−W]都标记为v,x代表节点,w代表重量,W为背包容量,v为价值
这样方便我们递归回溯时进行状态转移
接着我们一直遍历当前节点的子节点,将子节点进行dfs循环,直到不能遍历为止
这样我们就像上面所说的,遍历到4不能遍历,回溯到2的状态
接着进行01背包的状态转移方程,当前循环结束,在回溯到上一次的状态
最终dfs循环结束,输出 f [ r o o t ] [ W ] f[root][W] f[root][W]
接下来我们看代码:
code
const int N=1e3+5;
int w[N],v[N],f[N][N];
vector<int> g[N];
int n,W;
void dfs(int x){for(int i=w[x];i<=W;++i) f[x][i]=v[x];//将w~W的重量都标记为vfor(auto y : g[x]){dfs(y);//一直循环子节点,直到不能循环为止for(int j=W;j>=w[x];--j)for(int k=0;k<=j-w[x];++k){//所选的物品必须减去当前重量f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);//选子节点的物品还是不选子节点的物品}}
}
void solve(){cin >> n >> W;int root;for(int i=1;i<=n;++i){int x;cin >> w[i] >> v[i] >> x;if(x==-1) root=i;//标记else g[x].push_back(i);//建树}dfs(root);cout << f[root][W];return ;
}
背包问题求方案数
模板例题
背包问题求方案数
思路
这种类型的题目不需要我们求具体的价值,但是需要我们求最优价值的方案总数
那么我们首先还是需要算出最大的价值,然后将能到达当前价值的方案数进行相加
那么具体该如何实现呢?
我们需要在01背包的基础上,多开一个g数组,用于统计方案数
对于每步的状态来源,我们都有两种情况,一种是本身,一种是当前容量减去物品容量加上物品价值
这时我们新开一个变量temp,这个变量统计两种情况的最大值
若temp等于本身,那么 g [ i ] g[i] g[i]加上它本身
若temp等于当前容量减去物品容量加上物品价值,那么 g [ i ] + g [ j − w [ i ] g[i]+g[j-w[i] g[i]+g[j−w[i]
每次加上都记得要取模
然后将当前状态 f [ j ] f[j] f[j]更新为temp
最后找出背包所能容量的最大价值,遍历f数组,若当前 f [ i ] f[i] f[i]等于最大价值,加上 g [ i ] g[i] g[i]
接下来看代码进一步理解
code
const int N=1e3+5;
int f[N],g[N],w[N],v[N];
void solve(){int n,W;cin >> n >> W;for(int i=1;i<=n;++i){cin >> w[i] >> v[i];}g[0]=1;//若不选物品,方案数为1for(int i=1;i<=n;++i)for(int j=W;j>=w[i];--j){int temp=max(f[j],f[j-w[i]]+v[i]);//temp为当前状态的最大值int c=0;//统计数量if(temp==f[j]) c=(c+g[j])%mod;//加上方案数if(temp==f[j-w[i]]+v[i]) c=(c+g[j-w[i]])%mod;f[j]=temp,g[j]=c;//状态转移}int maxn=0;for(int i=0;i<=W;++i) maxn=max(maxn,f[i]);//找到最大价值int ans=0;for(int i=0;i<=W;++i){if(f[i]==maxn) ans=(ans+g[i])%mod;//统计个数}cout << ans;return ;
}
背包问题求具体方案
模板例题
背包问题求具体方案
思路
首先我们需要回溯到原来的状态,这时候我们开一维数组就会丢失原来的状态,这时候必须开二维数组来存储数据
我们先考虑一个问题,我们是从前往后回溯,还是从后往前回溯呢?
答案很明显,我们需要从前往后回溯
为什么呢?
题目要求输出字典序最小的方案
我们拿一个例子来说明:
3 3
1 2
2 4
2 4
物品总数为3,背包容量为3,每个物品先输入重量,在输入价值
如果我们从后往前回溯,那么我们求出的具体方案为1 3(最后将数组颠倒一下)
可是答案很明显为1 2,这样字典序才是最小的
那么我们就将这种方法pass掉
那么我们一开始需要第n件物品的状态转移到第1件物品,这样 f [ 1 ] [ W ] f[1][W] f[1][W]就为最大的价值
首先还是先套01背包的模板,只不过从1开始变为从n开始
然后我们从序号1遍历到序号n,判断当前的状态是不是由当前价值加上上一个状态转移过来的,即 f [ i ] [ j ] = = f [ i + 1 ] [ j − w [ i ] ] + v [ i ] f[i][j]==f[i+1][j-w[i]]+v[i] f[i][j]==f[i+1][j−w[i]]+v[i]
若满足,则当前背包容量减去 w [ i ] w[i] w[i],直接输出当前下标即可
接下来看代码
code
const int N=1e3+5;
int f[N][N],v[N],w[N],cnt[N];
void solve(){int n,W;cin >> n >> W;for(int i=1;i<=n;++i){cin >> w[i] >> v[i];}for(int i=n;i>=1;--i)//倒着来for(int j=0;j<=W;++j){f[i][j]=f[i+1][j];if(j>=w[i]) f[i][j]=max(f[i][j],f[i+1][j-w[i]]+v[i]);}for(int i=1,j=W;i<=n;++i){if(j>=w[i] && f[i][j]==f[i+1][j-w[i]]+v[i]){//判断状态cout << i << " ";j-=w[i];}}return ;
}
相关文章:

动态规划之——背包DP(完结篇)
文章目录 概要说明分组背包模板例题1思路code模板例题2思路code 有依赖的背包问题模板例题思路code 背包问题求方案数模板例题思路code 背包问题求具体方案模板例题思路code 概要说明 本文讲分组背包、有依赖的背包、 背包问题求方案数以及背包问题求具体方案 入门篇(01背包和…...

Advanced IP Scanner - 网络扫描工具介绍
Advanced IP Scanner 是一款免费、快速且用户友好的网络扫描工具。它能够帮助用户扫描局域网(LAN)中的所有设备,提供详细的设备信息,包括IP地址、MAC地址、设备名称和厂商信息。该工具对IT管理员和普通用户都非常有用,…...

数据库事务的四大特性ACID
数据库事务的四大特性ACID 数据库事务(Transaction)是数据库管理系统(DBMS)执行过程中的一个逻辑单位,由一个或多个SQL语句组成,这些语句作为一个整体一起向系统提交,要么全部执行,…...
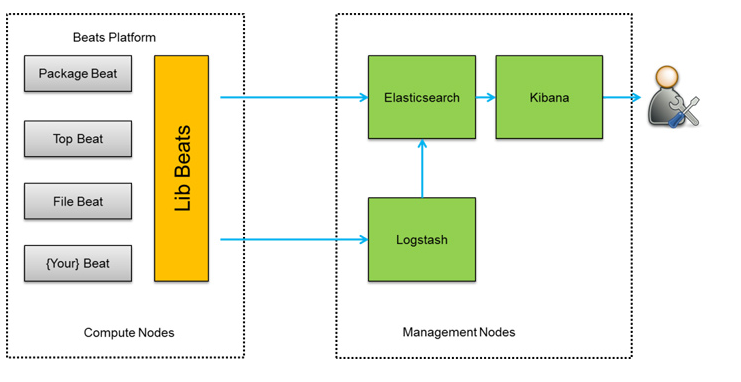
ELK架构介绍
一、ELK简介 ELK 是由三个开源软件组成的,分别是:Elasticsearch、Logstash和Kibana,这三个软件各自在日志管理和数据分析领域发挥着重要作用。Elasticsearch提供分布式存储和搜索能力;Logstash负责数据收集和处理,而K…...

Vscode下ESP32工程函数定义无法跳转
1.删除.vscode 2.按下 ctrlshiftp,搜索 ESP-IDF:Add vscode Configuration Folder...

liquibase.exception.LockException: Could not acquire change log lock.
项目场景: 启动应用花了好长时间,最后报出异常. 问题描述 启动应用花了好长时间,最后报出异常. 异常: Caused by: liquibase.exception.LockException: Could not acquire change log lock. Currently locked by LAPTOP-OQ9VB…...
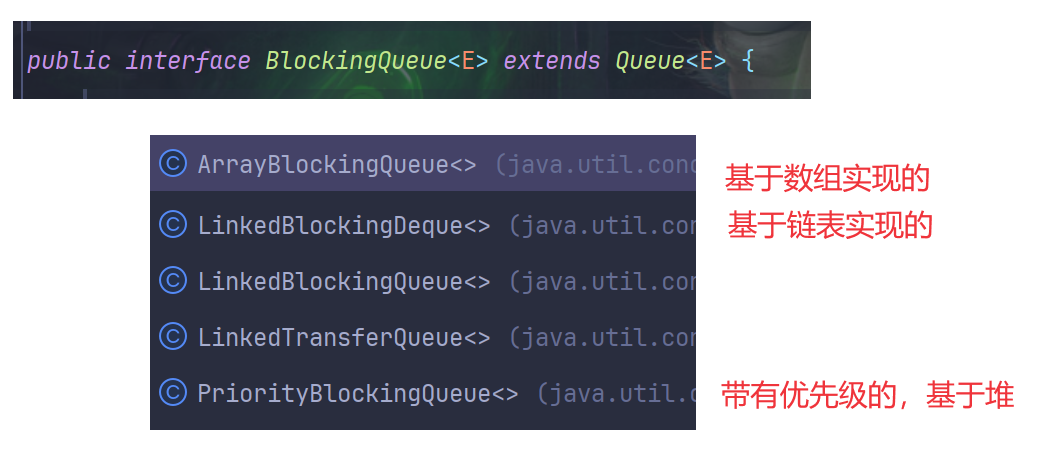
【多线程-从零开始-捌】阻塞队列,消费者生产者模型
什么是阻塞队列 阻塞队里是在普通的队列(先进先出队列)基础上,做出了扩充 线程安全 标准库中原有的队列 Queue 和其子类,默认都是线程不安全的 具有阻塞特性 如果队列为空,进行出队列操作,此时就会出现阻…...

数据结构——栈(Stack)
目录 前言 一、栈的概念 1、栈的基本定义 2、栈的特性 二、栈的基本操作 1.相关操作概念 2.实现方式 (1)顺序栈 (2)链式栈 三、栈的应用 总结 前言 栈(Stack)是一种常见且重要的数据结构,它遵循…...

修改pom.xml为阿里云仓库并且让他生效
一、项目pom.xml添加 <repositories><repository><id>aliyun-central</id><name>Aliyun Maven Central</name><url>https://maven.aliyun.com/repository/central</url></repository><repository><id>aliyu…...

step13:qml/qt程序打包
文章目录 0.文章介绍1.软件发布2.准备打包软件3.双击开始运行打包软件4.点击安装5.参考连接 0.文章介绍 1.软件发布 打包之前需要先发布,参考教程连接 2.准备打包软件 官方下载地址:http://www.jrsoftware.org/isdl.php#stable 下载之后一路点击下一…...
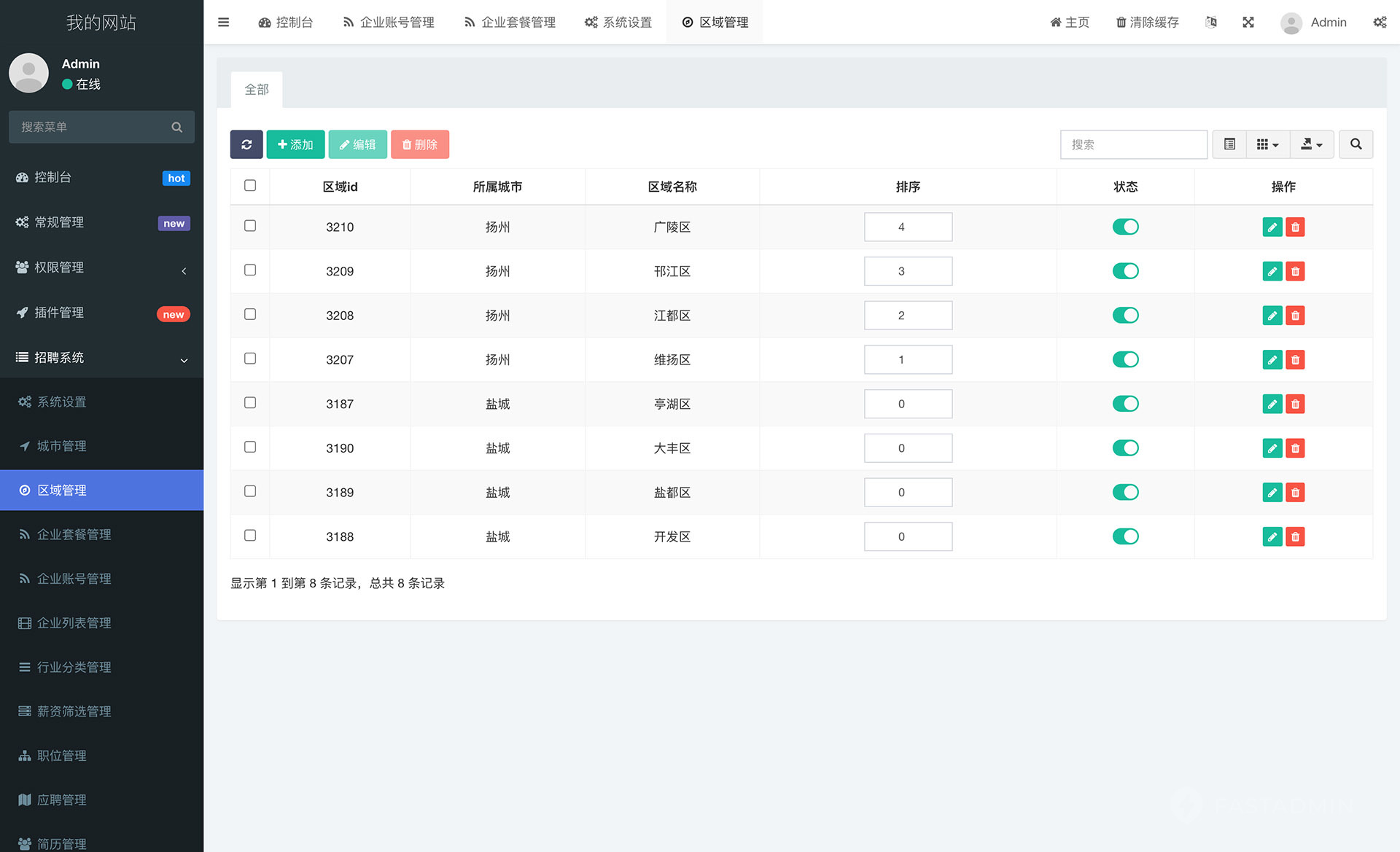
招聘求职小程序
本文来自:ThinkPHPFastAdmin招聘求职小程序 - 源码1688 应用介绍 一款基于ThinkPHPFastAdmin开发的原生微信小程序招聘管理系统。 前端小程序演示: 后台管理网址: https://fastadmin.site100.cn/PbfhegDBAJ.php/index/login 网盘链接&#x…...

10分钟学会docker安装与使用
文章目录 1、docker简介2、docker的基本组成3、docker的安装与配置4、docker的常用命令 1、docker简介 什么是容器? 它是一种虚拟化的方案,是操作系统级别的虚拟化,只能运行相同或相似内核的操作系统,依赖于Linux内核特性&#x…...

vue3、uniapp-vue3模块自动导入
没有使用插件 使用插件,模块自动导入 安装: npm i -D unplugin-auto-importvite.config.js (uniapp没有此文件,在项目根目录下创建) import { defineConfig } from "vite"; import uni from "dcloudio/vite-plugin-uni"; import AutoImport from &qu…...
)
Ubantu设置国内镜像(阿里云、华为云)
1. 确定系统版本 国内有很多 Ubuntu 的镜像源,包括阿里的、网易的,还有很多教育网的源,比如:清华源、中科大源等。 不同的 ubantu 版本对应的镜像源有所不同,所以需要先查看系统的版本号: lsb_release -a…...

Redis远程字典服务器(3)——常用数据结构和单线程模型
目录 一,常用数据结构 1.0 前言 1.1 string 1.2 hash 1.3 list 1.4 set 1.5 zset 1.6 演示 二,关于单线程模型 2.1 关于Redis的单线程 2.2 Redis为什么快 一,常用数据结构 1.0 前言 Redis是采用键值对的方式来存储数据的&#…...

[Qt][按钮类控件]详细讲解
目录 0.按钮状态说明1.Push Button2.Radio Button3.Check Box4.Tool Button 0.按钮状态说明 clicked:⼀次 ⿏标按下⿏标释放 触发pressed:鼠标按下时触发released:鼠标释放时触发toggled:checked属性改变时触发 1.Push Button QP…...

数据结构(5.5_2)——并查集
逻辑结构——数据元素之间的逻辑关系 并查集: 并查集(Union-Find)是一种树型的数据结构,用于处理一些不交集的合并及查询问题。它支持两种操作: 用双亲表示存储并查集 首先将所有根节点数组值设为-1,其…...

Java Web —— 第四天(Maven)
Maven是什么 Maven 的本质是一个项目管理工具,将项目开发和管理过程抽象成一个项目对象模型(POM) POM (ProjectObject Model): 项目对象模型 Maven的作用 项目构建:提供标准的、跨平台的自动化项目构建方式 依赖管理:方便快捷的管理项目依赖的资源 (ar包)&…...

2024年电脑录屏软件推荐:捕捉屏幕,记录生活,分享精彩
在众多电脑录屏软件中,如何挑选出一款适合自己的工具呢?今天,我们就来为大家对比评测四款热门电脑录屏软件:福昕REC、转转大师录屏、爱拍录屏和轻映录屏。通过对它们的功能、性能、操作便捷性等方面进行对比,帮助你找到…...

oracle 增删改查字段
在Oracle数据库中,对表字段的增删改查是数据库操作的基础。以下是关于Oracle中如何增加、删除、修改和查询字段的详细解释: 1. 增加字段(Add) 增加字段的语法为: ALTER TABLE 表名 ADD (字段名 数据类型 [DEFAULT 默…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
