代码随想录第二十四天|动态规划(8)
目录
LeetCode 300. 最长递增子序列
LeetCode 674. 最长连续递增序列
LeetCode 718. 最长重复子数组
LeetCode 1143. 最长公共子序列
LeetCode 1035. 不相交的钱
LeetCode 53. 最大子序和
LeetCode 392. 判断子序列
总结
LeetCode 300. 最长递增子序列
题目链接:LeetCode 300. 最长递增子序列
思想:依然用动归五部曲来分析,第一个dp数组的定义。这里把dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。在做递增比较的时候,比较两个子序列的结尾才能算递增,比较完一个再比较结尾也可以保证是递增的。其次就是状态转移方程,位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列+1的最大值。所以状态转移方程是if(nums[i] > nums[j]) dp[i]=max(dp[i],dp[j]+1)。初始化就把dp数组全初始化为1,因为本身也是一个子序列。这里有两层循环,先从前往后遍历整个nums数组,内层遍历就从前往后遍历到外层下标-1就行了。
代码如下:
int lengthOfLIS(vector<int>& nums) {if (nums.size() == 1) return 1;vector<int> dp(nums.size(), 1);int result = 0;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}result = dp[i] > result ? dp[i] : result;}return result;}时间复杂度:O(n^2),空间复杂度:O(n)。
LeetCode 674. 最长连续递增序列
题目链接:LeetCode 674. 最长连续递增序列
思想:本题跟上题基本上情况都是一模一样的,除了子序列变成了连续连续,也就是说任何递增序列的元素在原数组必须要相邻。那么把上述循环中的if判断条件修改了就行,改为if(dp[j+1]>dp[j])然后再进行状态判断,如果不满足递增的话,dp[i]就等于1就行了,因为要重新进行计算。
代码如下:
int findLengthOfLCIS(vector<int>& nums) {if (nums.size() == 1) return 1;vector<int> dp(nums.size(), 1);int result = 0;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[j+1] > nums[j]) dp[i] = max(dp[i], dp[j]+1);else dp[i] = 1;}result = dp[i] > result ? dp[i] : result;}return result;}时间复杂度:O(n^2),空间复杂度:O(n)。
LeetCode 718. 最长重复子数组
题目链接:LeetCode 718. 最长重复子数组
思想:本题没有强调连续的话,子数组就相当于子序列。那么还是动归五部曲,第一个确定dp[i]。dp[i][j]是以下标i-1为结尾的A和下标j-1为结尾的B,最长重复子数组长度为dp[i][j]。第二个就是确定递推公式,dp[i][j]需要i-1和j-1的状态推导出来,那么当A[i-1]=B[j-1]的时候,dp[i][j] = dp[i-1][j-1]+1。初始化的话就把每一个初始化为0就行了,循环就外层遍历一个数组,内层遍历另一个数组就可以了。
代码如下:
int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size()+1, vector<int>(nums2.size()+1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;result = dp[i][j] > result ? dp[i][j] : result;}}return result;}时间复杂度:O(n^2),空间复杂度:O(n^2)。
LeetCode 1143. 最长公共子序列
题目链接:LeetCode 1143. 最长公共子序列
思想:其实本题跟上题是差不多的,主要差别就是递推公式上,相等的就是一样的递推公式,这里存在着不等,不等的话就看i-1和j-1状态上的数值谁大,谁大就取谁。即dp[i][j] = max(dp[i-1][j], dp[i][j-1]。
代码如下:
int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size()+1, vector<int> (text2.size()+1, 0));int result = 0;for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i-1] == text2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i][j-1], dp[i-1][j]);result = dp[i][j] > result ? dp[i][j] : result;}}return result;}时间复杂度:O(n^2),空间复杂度:O(n^2)。
LeetCode 1035. 不相交的钱
题目链接:LeetCode 1035. 不相交的钱
思想:本题跟上题一模一样。遂不再重复。
代码如下:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size()+1, vector<int>(nums2.size()+1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);result = dp[i][j] > result ? dp[i][j] : result;}}return result;}时间复杂度:O(n^2),空间复杂度:O(n^2)。
LeetCode 53. 最大子序和
题目链接:LeetCode 53. 最大子序和
思想:还是动归五部曲吧,第一步确定dp数组。这里dp[i]表示包括下标i的最大连续子序列和dp[i]。其次就是递推公式,dp[i]只有两个方向可以推出来:第一个状态当前nums[i]加入子序列即dp[i] = dp[i-1] + nums[i];第二个状态是重新开始计算子序列即dp[i] = nums[i]。这俩个状态取最大就行了。初始化只需要初始化dp[0]就行了,dp[0]很明显要等于nums[0]。遍历顺序就直接从前往后遍历就行了。
代码如下:
int maxSubArray(vector<int>& nums) {if (nums.size() == 1) return nums[0];vector<int> dp(nums.size(), INT_MIN);dp[0] = nums[0];int result = dp[0];for (int i = 1; i < nums.size(); i++) {dp[i] = max(dp[i-1] + nums[i], nums[i]);result = dp[i] > result ? dp[i] : result;}return result;}时间复杂度:O(n),空间复杂度:O(n)。
LeetCode 392. 判断子序列
题目链接:LeetCode 392. 判断子序列
思想:本题其实跟判断最长子序列是一个道理,只需最后判断得出的长度是否等于s的长度就行了。遂不再讲解了。
代码如下:
bool isSubsequence(string s, string t) {if (s.size() > t.size()) return false;vector<vector<int>> dp(s.size()+1, vector<int> (t.size()+1, 0));for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = max(dp[i][j-1], dp[i-1][j]);}}if (dp[s.size()][t.size()] == s.size()) return true;return false;}时间复杂度:O(n^2),空间复杂度:O(n^2)。
总结
我还是不会!!!
相关文章:
)
代码随想录第二十四天|动态规划(8)
目录 LeetCode 300. 最长递增子序列 LeetCode 674. 最长连续递增序列 LeetCode 718. 最长重复子数组 LeetCode 1143. 最长公共子序列 LeetCode 1035. 不相交的钱 LeetCode 53. 最大子序和 LeetCode 392. 判断子序列 总结 LeetCode 300. 最长递增子序列 题目链接&#…...

编程-设计模式 3:单例模式
设计模式 3:单例模式 定义与目的 定义:单例模式确保一个类只有一个实例,并提供一个全局访问点来访问该实例。目的:这种模式通常用于那些需要频繁访问且只需一个实例的对象,例如配置管理器、日志记录器等。 实现示例…...

Kaniko 构建 Docker 镜像
Kaniko 主要用于构建 Docker 镜像,而不是运行程序。它的主要用途是从 Dockerfile 构建容器镜像,但它并不负责运行容器或程序。以下是 Kaniko 的主要功能和局限性: 主要功能 构建镜像:Kaniko 从 Dockerfile 构建容器镜像。它通过…...

Javascript常见算法(每日两个)
合并两个有序链表 在JavaScript中,合并两个有序链表通常指的是将两个已经按照某种顺序(如升序或降序)排列的链表合并成一个新的有序链表。由于JavaScript本身不直接支持链表数据结构,我们通常会用对象或数组来模拟链表的行为。但…...
Spring -- 事务
Spring中事务的操作分为两类:(1)编程式事务 – 手动写代码操作事务(2)声明式事务 – 利用注解开启事务和提交事务 1. 编程式事务 准备Controller RestController RequestMapping("/user") public class UserInfoController {Autowiredprivate UserInfoService use…...
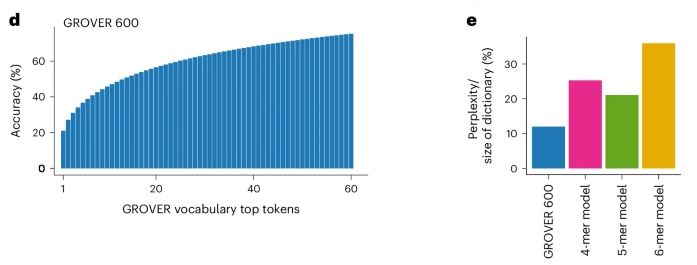
生命密码的破译者:AI如何学会读懂DNA语言?
引言 如果能像解读一本神秘的书籍那样,理解DNA的“语言”,将是多么令人兴奋的科学突破!如今,这正在逐步变为现实。科学家们训练出的AI模型GROVER正如一个勤奋的学生,学习着DNA的每一个“单词”和“语法”,…...

大数据信用报告查询哪家平台的比较好?
相信在搜索大数据信用的你,已经因为大数据信用不好受到了挫折,想详细了解一下自己的大数据信用,但是找遍了网络上的平台之后才发现,很多平台都只提供查询服务,想要找一个专业的平台查询和讲解很困难。下面本文就为大家…...

Java高级Day24-集合最后补充
75.HashTable 基本介绍: 存放元素的健值对 即K-V hashtable的键和值都不能为null,否则会抛出NullPointerException hashtable使用方法基本上和HashMap一样 hashtable是线程安全的,hashmap是线程不安全 扩容机制: 底层有数组…...

C++入门:C语言到C++的过渡
前言:C——为弥补C缺陷而生的语言 C起源于 1979 年,当时 Bjarne Stroustrup 在贝尔实验室工作,面对复杂软件开发任务,他感到 C 语言在表达能力、可维护性和可扩展性方面存在不足。 1983 年,Bjarne Stroustrup 在 C 语言…...

了解MVCC
概念 MVCC,全称Multi-Version Concurrency Control,即多版本并发控制,是一种并发控制的方法,维护一个数据的多个版本,使得读写操作没有冲突,快照读为MySQL实现MVCC提供了一个非阻塞读功能。MVCC的具体实现…...

WPF自定义控件的应用(DynamicResource的使用方法)
1 DynamicResource的使用方法 可以在字典文件 的抬头区写入数: <SolidColorBrush x:Key"PrimaryBackgroundColor" Color"#FFABAdB3"/><SolidColorBrush x:Key"TextBox.MouseOver.Border" Color"#FF7EB4EA"/>&l…...

Postgresql数据库密码忘记的解决
当您忘记PostgreSQL数据库的密码时,可以通过以下步骤来重置密码。这些步骤在Windows和Linux操作系统上大体相同,但具体操作路径和命令可能有所不同。 步骤一:找到并修改pg_hba.conf文件 定位安装目录: Windows:通常在PostgreSQL的安装目录下的data文件夹中。Linux:位置可…...

Flink SQL 基础操作
Flink SQL是建立在Apache Flink之上的SQL处理引擎,它允许用户以SQL的方式处理流数据和批数据。以下是一些Flink SQL的基础操作: 一、环境准备 1.启动flink集群 ./start-cluster.sh启动sql-client ./sql-client.sh二、数据源定义 创建表(…...

海思AE模块Lines_per_500ms参数的意义
基础知识 1秒(S)1000毫秒(ms)1000_000微妙(s)1000_000_000纳秒(ns) 1GHz1000Mhz1000_000KHz1000_000_000Hz 1Hz1/s 抗频闪原理 海思AE模块参数中有一个LinesPer500ms的参数,意思为500ms对应的曝光行数。此个参数和抗频闪有关。 我们知道: 50HZ…...

【代码随想录】区间和——前缀和方法
本博文为《代码随想录》学习笔记,原文链接:代码随想录 题目 原题链接:58. 区间和(第九期模拟笔试) 题目描述 给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。 输入描述 第一行输入为…...

Bug 解决 | 前端项目无法正确安装依赖?
目录 1、网络问题 2、权限问题 3、版本冲突 4、缓存问题 5、依赖配置错误 6、系统环境问题 前端项目和后端项目一样,都需要用到很多第三方的类库依赖。目前基本上我们主流的前端项目都使用 Npm、Yarn 等包管理工具来管理项目依赖,正常情况下通过执…...

【mysql 第四篇章】bin log 的作用是啥呢?
一、redo Log 介绍 redo log 是一种偏向物理性质的重做日志,因为他里面记录类似的这样的东西,“对那个数据也中的什么记录,做了个什么修改”。它是 InnoDB 存储引擎特有的东西。 二、bin Log 日志 bin log 叫做归档日志,它里面…...

Linux 操作系统:基于环形队列的生产者消费者模型
Linux 操作系统:基于环形队列的生产者消费者模型 一、前言二、大致框架二、P操作、V操作三、生产者生产数据四、生产者获取数据五、代码测试六、所有代码 一、前言 环形队列采用数组模拟,用模运算来模拟环状特性。和基于阻塞队列的生产者消费者模型不同的…...

python求解二次方程
为了找到x和y之间的关系,并假设这种关系是一个二次函数,我们可以使用numpy的polyfit函数来拟合一个二次方程(即形式为y ax^2 bx c的方程)。然后,我们可以使用matplotlib来绘制散点图,并在图上添加最佳拟…...

Spring框架面试总结
Spring基础 什么是spring框架 Spring 框架是一个用于构建企业级 Java 应用程序的开源框架。【Java项目快速构建轻量级框架】我们一般说 Spring 框架指的都是 Spring Framework,它是很多模块的集合,使用这些模块可以很方便地协助我们进行开发。【根据模…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
