堆的实现(偷懒版)

🌹个人主页🌹:喜欢草莓熊的bear
🌹专栏🌹:数据结构

目录
前言
一、堆的实现
1.1 堆的向下调整算法
思路:
1.2 堆的向上调整算法
1.3 堆的创建
1.4 堆的复杂度计算
向下调整建堆的复杂度:
向上调整建堆的复杂度:
1.5 堆的插入
1.6 堆的删除
1.7 堆的代码实现
总结
前言
在上期内容介绍了二叉树、还简单提了一下堆的概念和大堆、小堆。回顾一下堆是首先是完全二叉树,因为是完全二叉树所以使用数组储存比较合理。
一、堆的实现
1.1 堆的向下调整算法
int arr[] = {27,15,19,18,28,34,65,49,25,37};
上面这幅图就是向下调整的算法的过程图
思路:
假设我们通过向下调整算法建立小堆,我们就需要从根的左右子树开始,比较得出左右子树小的那一个和根比较,谁小谁就是根。我们之前还介绍父亲节点和孩子节点的概念,我们这里就要使用到。根据我们上面的思路,向下调整算法需要通过比较还在节点后进行调整。所以我们需要知道父亲节点然后再找到孩子节点为什么要知道父亲节点呢?我们通过数组储存着堆,下标就可以帮助我们找到孩子节点。

大致思路就是这样我们来写代码:
void Swap(HPDataType* x, HPDataType* y)//交换数据
{HPDataType tmp = *x;*x = *y;*y = tmp;
}void ADjustDown(HPDataType* a, int n,int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){//假设法if (a[child] > a[child + 1] && child + 1 < n)//比较左右子树,找到较小的子树。{child++;}if (a[parent] > a[child])//数据交换{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}解释一下个别代码,child + 1 < n 防止数组越界。
1.2 堆的向上调整算法

向上调整我们需要从最后一层向上调整,所以我们是通过孩子节点得到父亲节点。大致思路和向下调整一样,比较孩子节点的大小后再和父亲节点比较一直比较到根节点。根据child = parent *2+1 反推得到 parent = ( child -1 )/2 。
直接上代码:
void Swap(HPDataType* x, HPDataType* y)//交换数据
{HPDataType tmp = *x;*x = *y;*y = tmp;
}void ADjustUp(HPDataType* a,int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent= (child - 1) / 2;}else{break;}}
}1.3 堆的创建
int a[] = {1,5,3,8,7,6};
1.4 堆的复杂度计算
向下调整建堆的复杂度:

向上调整建堆的复杂度:
是O(N) = N * logN 得到方法和向下调整一样推导就可以了。
1.5 堆的插入

堆的插入需要用的向上调整
1.6 堆的删除

1.7 堆的代码实现
堆的初始化、销毁都是很简单和之前写的栈啊等等都十分相似。剩下一些 获取堆顶元素、堆的个数、堆的判断都比较简单就不讲解了给上了代码。
typedef int HPDataType;typedef struct Heap//因为堆的定义就是满二叉树与完全二叉树,用数组储存非常好。
{HPDataType* a;//数组int size;int capacity;
}Heap;//小堆情况下的初始化
void HPInit(Heap* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//销毁
void HPDestory(Heap* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}void Swap(HPDataType* x, HPDataType* y)//交换数据
{HPDataType tmp = *x;*x = *y;*y = tmp;
}void ADjustUp(HPDataType* a,int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent= (child - 1) / 2;}else{break;}}
}void ADjustDown(HPDataType* a, int n,int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){//假设法if (a[child] > a[child + 1] && child + 1 < n){child++;}if (a[parent] > a[child]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//入堆
void HPPush(Heap* php, HPDataType x)
{assert(php);//扩容if (php->size == php->capacity){int Newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, Newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("ralloc fail");return;}php->a = tmp;php->capacity = Newcapacity;}php->a[php->size++] = x; ADjustUp(php->a,php->size - 1);
}//出堆(消除堆顶数据)
void HPPop(Heap* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;ADjustDown(php->a,php->size,0);
}//取堆顶数据
HPDataType HPTop(Heap* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//堆的数据个数
int HPSize(Heap* php)
{assert(php);return php->size;
}//堆的判空
bool HPEmpty(Heap* php)
{assert(php);return php->size == 0;
}总结
本节重点堆的向上、向下调整算法的代码实现 和 复杂度计算。
相关文章:

堆的实现(偷懒版)
🌹个人主页🌹:喜欢草莓熊的bear 🌹专栏🌹:数据结构 目录 前言 一、堆的实现 1.1 堆的向下调整算法 思路: 1.2 堆的向上调整算法 1.3 堆的创建 1.4 堆的复杂度计算 向下调整建堆的复杂度…...

一键启动,智能分拣:3D视觉系统赋能多SKU纸箱高效混拆作业
在快速发展的电商时代,仓储物流面临着前所未有的挑战。尤其是面对成千上万种不同的纸箱,如何实现快速、准确、高效的混拆作业,成为了众多企业亟待解决的问题。幸运的是,随着科技的进步,3D视觉系统正逐步成为这一领域的…...

unity草体渲染方案 GPU Instaning
有一天看项目里的FrameDebug发现在森林系的场景里草体的drawcall差不多有100多 主要是因为灯光贴图,位置等不一样导致的打断合批,导致一个批次只能渲染10个左右的草体 之前有了解过unity有接口(Graphics.DrawMeshInstanced)可以把…...
最近在西安召开的学术会议:EI检索超快,信息系统与计算技术领域!
第十二届信息系统与计算技术国际会议(ISCTech 2024)将于2024年11月8日-11月11日在中国西安盛大举行,由长沙理工大学主办,同济大学、西北工业大学联合协办。会议聚焦信息系统与计算技术等相关研究领域,广泛邀请国内外知…...

sRGB和伽马矫正
sRGB和伽马矫正 1. sRGB的含义: sRGB是一种色彩空间,全称为“标准红色-绿色-蓝色”(standard Red Green Blue)。它由惠普和微软在1996年共同开发,用于确保不同设备上色彩的一致性。 在sRGB中,“s”代表“…...

Summer School science communication project--Laptop Selection Suggestion
目录 Introduction Audiance Usage CPU What is a central processing unit (CPU) Notable makers of CPUs GPU Graphics Card: GPU The classifications of graphics cards The brands of graphics cards Dedicated Graphics Cards GeForce MX Series: GeForc…...

网络编程概念详解模拟回显客户端服务器
目录 1.网络中重要的概念 1)IP地址: 2)端口号: 3)协议 协议分层 OSI七层模型(教科书) TCP/IP五层模型 封装和分用 网络套接字 面试题:TCP/UDP的区别? UDP数据报套接字编程 模拟一个回…...
)
代码随想录第二十四天|动态规划(8)
目录 LeetCode 300. 最长递增子序列 LeetCode 674. 最长连续递增序列 LeetCode 718. 最长重复子数组 LeetCode 1143. 最长公共子序列 LeetCode 1035. 不相交的钱 LeetCode 53. 最大子序和 LeetCode 392. 判断子序列 总结 LeetCode 300. 最长递增子序列 题目链接&#…...

编程-设计模式 3:单例模式
设计模式 3:单例模式 定义与目的 定义:单例模式确保一个类只有一个实例,并提供一个全局访问点来访问该实例。目的:这种模式通常用于那些需要频繁访问且只需一个实例的对象,例如配置管理器、日志记录器等。 实现示例…...

Kaniko 构建 Docker 镜像
Kaniko 主要用于构建 Docker 镜像,而不是运行程序。它的主要用途是从 Dockerfile 构建容器镜像,但它并不负责运行容器或程序。以下是 Kaniko 的主要功能和局限性: 主要功能 构建镜像:Kaniko 从 Dockerfile 构建容器镜像。它通过…...

Javascript常见算法(每日两个)
合并两个有序链表 在JavaScript中,合并两个有序链表通常指的是将两个已经按照某种顺序(如升序或降序)排列的链表合并成一个新的有序链表。由于JavaScript本身不直接支持链表数据结构,我们通常会用对象或数组来模拟链表的行为。但…...
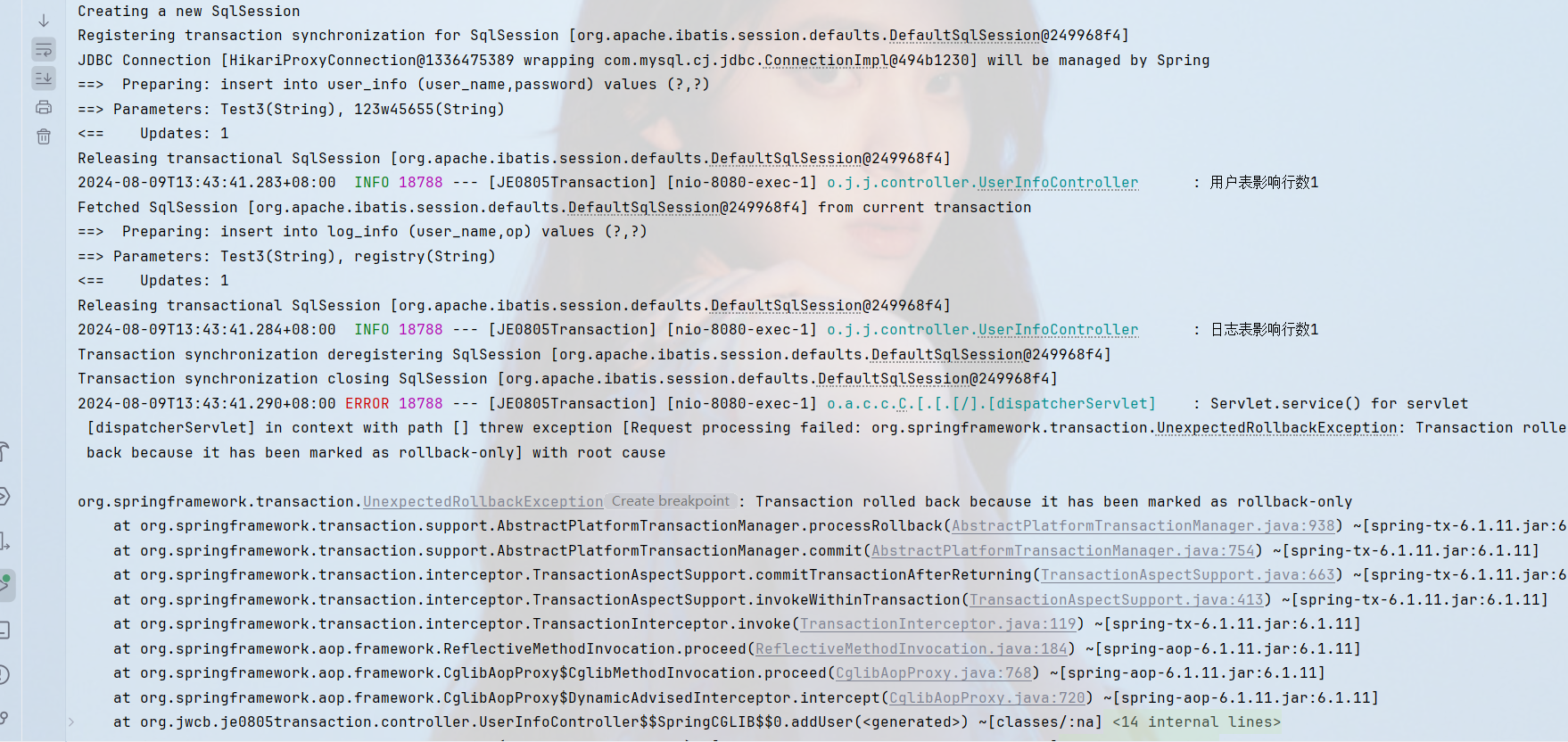
Spring -- 事务
Spring中事务的操作分为两类:(1)编程式事务 – 手动写代码操作事务(2)声明式事务 – 利用注解开启事务和提交事务 1. 编程式事务 准备Controller RestController RequestMapping("/user") public class UserInfoController {Autowiredprivate UserInfoService use…...
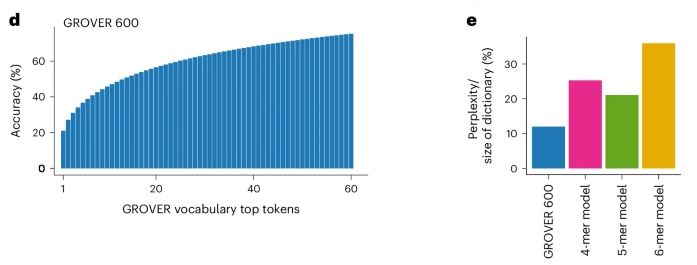
生命密码的破译者:AI如何学会读懂DNA语言?
引言 如果能像解读一本神秘的书籍那样,理解DNA的“语言”,将是多么令人兴奋的科学突破!如今,这正在逐步变为现实。科学家们训练出的AI模型GROVER正如一个勤奋的学生,学习着DNA的每一个“单词”和“语法”,…...

大数据信用报告查询哪家平台的比较好?
相信在搜索大数据信用的你,已经因为大数据信用不好受到了挫折,想详细了解一下自己的大数据信用,但是找遍了网络上的平台之后才发现,很多平台都只提供查询服务,想要找一个专业的平台查询和讲解很困难。下面本文就为大家…...

Java高级Day24-集合最后补充
75.HashTable 基本介绍: 存放元素的健值对 即K-V hashtable的键和值都不能为null,否则会抛出NullPointerException hashtable使用方法基本上和HashMap一样 hashtable是线程安全的,hashmap是线程不安全 扩容机制: 底层有数组…...

C++入门:C语言到C++的过渡
前言:C——为弥补C缺陷而生的语言 C起源于 1979 年,当时 Bjarne Stroustrup 在贝尔实验室工作,面对复杂软件开发任务,他感到 C 语言在表达能力、可维护性和可扩展性方面存在不足。 1983 年,Bjarne Stroustrup 在 C 语言…...

了解MVCC
概念 MVCC,全称Multi-Version Concurrency Control,即多版本并发控制,是一种并发控制的方法,维护一个数据的多个版本,使得读写操作没有冲突,快照读为MySQL实现MVCC提供了一个非阻塞读功能。MVCC的具体实现…...

WPF自定义控件的应用(DynamicResource的使用方法)
1 DynamicResource的使用方法 可以在字典文件 的抬头区写入数: <SolidColorBrush x:Key"PrimaryBackgroundColor" Color"#FFABAdB3"/><SolidColorBrush x:Key"TextBox.MouseOver.Border" Color"#FF7EB4EA"/>&l…...

Postgresql数据库密码忘记的解决
当您忘记PostgreSQL数据库的密码时,可以通过以下步骤来重置密码。这些步骤在Windows和Linux操作系统上大体相同,但具体操作路径和命令可能有所不同。 步骤一:找到并修改pg_hba.conf文件 定位安装目录: Windows:通常在PostgreSQL的安装目录下的data文件夹中。Linux:位置可…...

Flink SQL 基础操作
Flink SQL是建立在Apache Flink之上的SQL处理引擎,它允许用户以SQL的方式处理流数据和批数据。以下是一些Flink SQL的基础操作: 一、环境准备 1.启动flink集群 ./start-cluster.sh启动sql-client ./sql-client.sh二、数据源定义 创建表(…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
