算法板子:欧拉函数——求一个数的欧拉函数、线性时间内求1~n所有数的欧拉函数
目录
1. 欧拉函数
(1)概念
(2)性质
(3)计算公式
2. 求一个数的欧拉函数
(1)模拟过程
(2)代码
3. 线性时间内求1~n所有数的欧拉函数——筛法求欧拉函数
(1)要点
(2)代码
1. 欧拉函数
(1)概念
给一个整数n,求n的欧拉函数就是求1~n中有几个数和n互质。互质就是两个整数除了1以外没有其他的公约数。
![]()
(2)性质

(3)计算公式

2. 求一个数的欧拉函数
(1)模拟过程

(2)代码
#include <iostream>
using namespace std;// 求x这个数的欧拉函数
int phi(int x)
{// res代表1~x中与x互质的数的个数int res = x;// i从2枚举到根号xfor (int i = 2; i <= x / i; i ++ ){// 如果i是x的质因子if (x % i == 0){// 记得先除质因子再乘质因子减一; 先乘法可能会爆intres = res / i * (i - 1);while (x % i == 0) x /= i;}}// 如果最终x>1, 代表最终x也是原x的质因子; 所以就除质因子再乘质因子减一if (x > 1) res = res / x * (x - 1);return res;
}int main()
{int n;cin >> n;while (n --){int x;cin >> x;cout << phi(x) << endl;}return 0;
}3. 线性时间内求1~n所有数的欧拉函数——筛法求欧拉函数
(1)要点
可以在线性的时间内求出1~n所有数的欧拉函数,时间复杂度比上一种更小,模版类似筛法求质数。
(2)代码
#include <iostream>
using namespace std;const int N = 1e6 + 10;
int n;// vis[i]代表i这个数是否是合数; vis[4]=1代表4这个数是合数, vis[3]=0代表3这个数是质数
// p[i]代表第1~n中i个质数的值; p[1]=2代表1~n中第1个质数是2
// cnt代表1~n中质数的个数
int vis[N], p[N], cnt;
// phi[i]代表i这个数的欧拉函数; phi[5]=4代表5这个数的欧拉函数为4(跟5互质的数有1,2,3,4)
int phi[N];// 求1~n所有数的欧拉函数
void get_phi(int n)
{// 特判1的欧拉函数phi[1] = 1;// 求2~n所有数的欧拉函数for (int i = 2; i <= n; i ++ ){// 如果i是质数, 记录在p数组中, 并且质数的欧拉函数是质数减一if (!vis[i]) p[ ++ cnt] = i, phi[i] = i - 1;// j从1开始枚举for (int j = 1; 1LL * i * p[j] <= n; j ++ ){// 记录i*p[j]是合数vis[i * p[j]] = 1;// 求i*p[j]的欧拉函数if (i % p[j] == 0) {phi[i * p[j]] = phi[i] * p[j];break;}else phi[i * p[j]] = phi[i] * (p[j] - 1);}}
}int main()
{cin >> n;// 得到1~n所有数的欧拉函数, 记录在phi数组中get_phi(n);long long res = 0;for (int i = 1; i <= n; i ++ ) res += phi[i];cout << res << endl;return 0;
}相关文章:

算法板子:欧拉函数——求一个数的欧拉函数、线性时间内求1~n所有数的欧拉函数
目录 1. 欧拉函数 (1)概念 (2)性质 (3)计算公式 2. 求一个数的欧拉函数 (1)模拟过程 (2)代码 3. 线性时间内求1~n所有数的欧拉函数——筛法求欧拉函…...

2024牛客暑期多校训练营8
文章目录 A. Haitang and GameE.Haitang and MathJ. Haitang and TriangleK. Haitang and Ava A. Haitang and Game 通过审题可以知道,最后的胜者和若干次操作后最多能增加的数的奇偶有关。 由于 a i a_i ai 较小,所以我们枚举每一个没出现过的 x …...

git的一些操作指令
一、git 提交规范 commit message subject : 空格 message 主体 feat: 新功能(feature)用于提交新功能。fix: 修复 bug用于提交 bug 修复。docs: 文档变更用于提交仅文档相关的修改。style: 代码风格变动(不影响代码逻辑&…...

【IT行业研究报告】Internet Technology
一、引言 随着信息技术的飞速发展,IT行业已成为全球经济的重要驱动力。从云计算、大数据、人工智能到物联网,IT技术正深刻改变着各行各业的生产方式、商业模式和人们的生活方式。本报告旨在深入分析IT行业的现状、发展趋势和挑战,探讨其在各…...
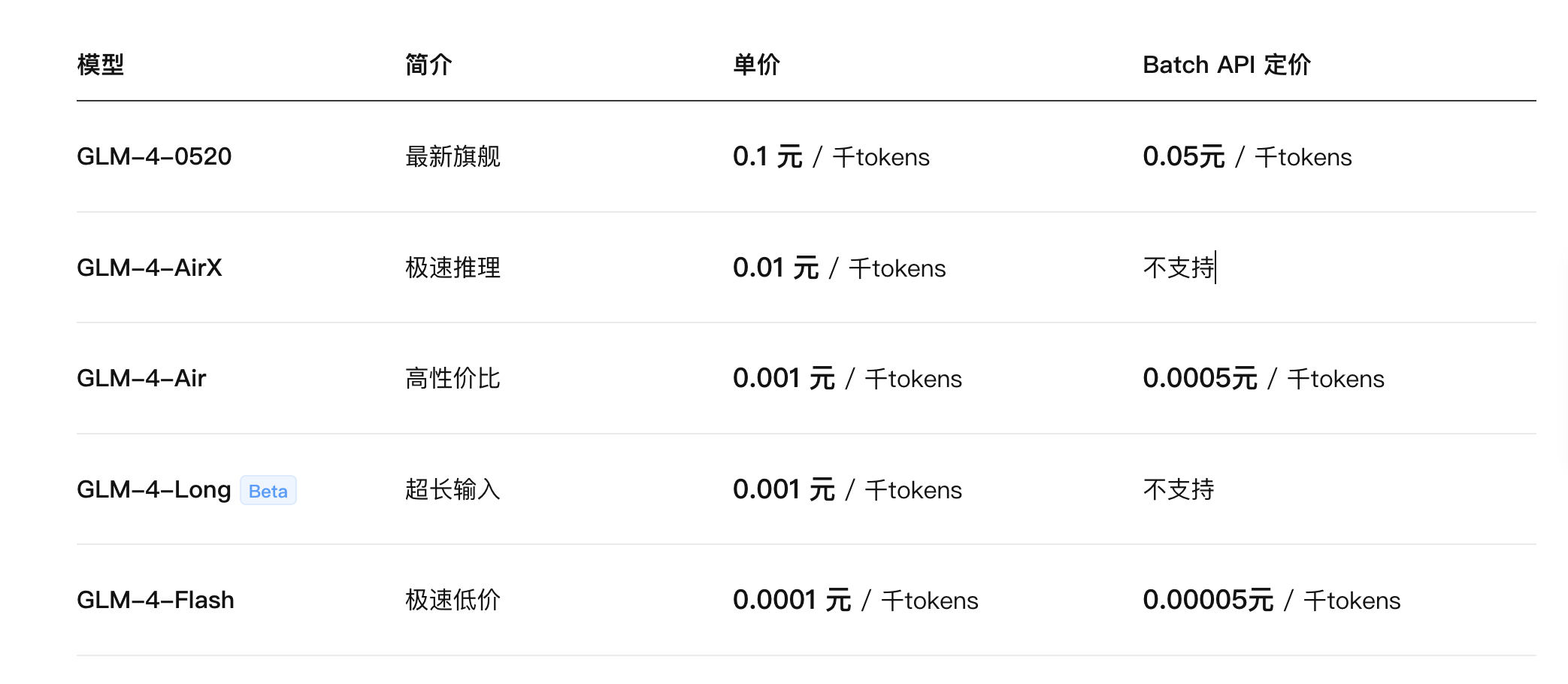
GLM大模型的机器翻译能力测试
背景介绍 最近想对GLM-4今年发布的几个大模型 glm-4-0520,glm-4-air以及glm-4-flash简单评测一下它们的机器翻译能力,由于这几个大模型的容量和训练数据都有区别,所以它们的翻译能力也是不同的。我们这里就分别选择一些有趣的,有…...

【硬件产品经理】汽车A样设计
目录 简介 制造方式 作者简介 简介 一般被称作原型样件(Prototype)。 主要是根据系统需求设计,实现基本功能和关键尺寸,用于基本功能的验证,用于初期产品软件调试和Hil台架测试(Hardware in Loop,硬件在环)的样机阶段。 也就说在设计初期,A样的主要目的可以划分…...

Ubuntu22.04系统中安装机器人操作系统ROS
在Ubuntu 22.04上安装ROS(Robot Operating System)的过程可以分为几个主要步骤。请注意,ROS有不同的版本(如ROS 1的Melodic、Noetic等,以及ROS 2的Foxy、Humble等),这些版本对Ubuntu的支持程度可…...

LeetCode54题:螺旋矩阵(原创)
【题目描述】 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2: 输入:mat…...

FPGA常见型号
FPGA(现场可编程门阵列)开发板种类繁多,涵盖了从入门级教育用途到高性能工业应用的广泛领域。以下是一些常见的 FPGA 开发板型号及其特点: 1. Xilinx(赛灵思)系列 Xilinx 是 FPGA 领域的领导者之一&#…...

【多模态大模型】FlashAttention in NeurIPS 2022
一、引言 论文: FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness 作者: Stanford University 代码: FlashAttention 特点: 该方法提出将Q、K、V拆分为若干小块,使执行注意力时不需要频…...

过滤器doFilter 方法
在Java EE中,过滤器的放行是指在过滤器的 doFilter 方法中调用 FilterChain 对象的 doFilter 方法,将请求传递给下一个过滤器或目标 servlet 进行处理。这个过程可以理解为过滤器的责任链传递。 过滤器的 doFilter 方法 在过滤器中,实现 Fil…...

WPF篇(9)-CheckBox复选框+RadioButton单选框+RepeatButton重复按钮
CheckBox复选框 CheckBox继承于ToggleButton,而ToggleButton继承于ButtonBase基类。 案例 前端代码 <StackPanel Orientation"Horizontal" HorizontalAlignment"Center" VerticalAlignment"Center"><TextBlock Text"…...

【机器学习基础】线性回归
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,…...

java基础概念12-二维数组
一、二维数组的定义 二维数组可以被视为数组的数组,即每个元素都是一个数组。 二维数组的应用场景: 当我们需要把数据分组管理的时候,就需要用到二维数组。 二、二维数组的初始化 2-1、静态初始化 阿里巴巴规范手册: // 静态初始…...

56 锐键交换机开局
锐键交换机开局 一 锐键视图切换 1 Ruijie> 用户视图 2 Ruijie# 特权模式 3 Ruijie(config)# 全局配置模式 4 Ruijie(config-if-GigabitEthernet 1/1/1)# 接口配置模式 5 Ruijie(config)#show vlan 6 exit (退出) 7 enable(进入)...

VR虚拟展厅与传统实体展厅相比,有哪些优势?
视创云展虚拟展厅相比传统的实体展厅具有多方面的优势,主要体现在以下几个方面: 1、降低成本: 虚拟展厅无需租赁或建设物理空间,减少了场地、装修和维护等方面的开支。同时,参观者和参展商无需现场参观或布展&#x…...

Vue的事件处理、事件修饰符、键盘事件
目录 1. 事件处理基本使用2. 事件修饰符3. 键盘事件 1. 事件处理基本使用 使用v-on:xxx或xxx绑定事件,其中xxx是事件名,比如clickmethods中配置的函数,都是被Vue所管理的函数,this的指向是vm或组件实例对象 <!DOCTYPE html&g…...
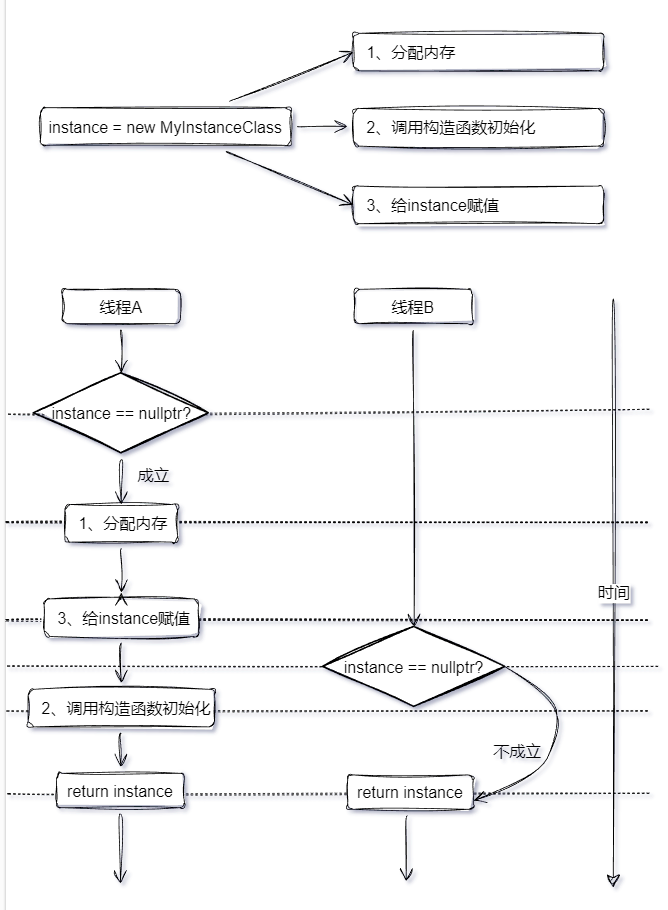
c++单例实践
C单例实践 在日常开发中,虽然太多的单例调用会让代码的耦合度变高,但是例如日志类这种,单例模式就变得非常有。所以这篇文章为大家介绍static 关键字相关知识以及如何实现自己的C单例类。 static关键字 首先让我们请出今天的主角: static。…...

SQL注入实例(sqli-labs/less-9)
0、初始页面 1、爆库名 使用python脚本 def inject_database1(url):name for i in range(1, 20):low 32high 128mid (low high) // 2while low < high:payload "1 and if(ascii(substr(database(),%d,1)) > %d ,sleep(2),0)-- " % (i, mid)res {"…...

http不同类型方法的作用,get和post区别
在HTTP协议中,不同的请求方法用于不同的操作。常见的HTTP方法包括GET、POST、PUT、DELETE、HEAD、OPTIONS、PATCH等,每种方法有其特定的作用。 常见的HTTP方法及其作用 1. GET - **作用**: 从服务器请求指定资源。GET方法通常用于获取数据而不会修改数据…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
