【代码随想录训练营第42期 Day24打卡 回溯Part3 - LeetCode 93.复原IP地址 78.子集 90.子集II
目录
一、做题心得
二、题目与题解
题目一:93.复原IP地址
题目链接
题解:回溯--分割问题
题目二:78.子集
题目链接
题解:回溯--子集问题
题目三:90.子集II
题目链接
题解:回溯--子集问题
三、小结
一、做题心得
今天的题个人感觉第一道 93. 复原 IP 地址 - 力扣(LeetCode)还是挺有难度的,虽然跟昨天打卡的分割回文串很相似,但是自己做的时候还是有点吃力。后边两道题就很简单了,感觉和前两天练的组合问题差不多,个人感觉问题不大。
这里直接开始今天的题目吧。
二、题目与题解
题目一:93.复原IP地址
题目链接
93. 复原 IP 地址 - 力扣(LeetCode)
有效 IP 地址 正好由四个整数(每个整数位于
0到255之间组成,且不能含有前导0),整数之间用'.'分隔。
- 例如:
"0.1.2.201"和"192.168.1.1"是 有效 IP 地址,但是"0.011.255.245"、"192.168.1.312"和"192.168@1.1"是 无效 IP 地址。给定一个只包含数字的字符串
s,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在s中插入'.'来形成。你 不能 重新排序或删除s中的任何数字。你可以按 任何 顺序返回答案。示例 1:
输入:s = "25525511135" 输出:["255.255.11.135","255.255.111.35"]示例 2:
输入:s = "0000" 输出:["0.0.0.0"]示例 3:
输入:s = "101023" 输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]提示:
1 <= s.length <= 20s仅由数字组成
题解:回溯--分割问题
这个题也是很明显的分割问题。 、
分析题意:有效IP地址分为4个部分,每一部分由.隔开,每一部分都有限制要求(这个限制要求往往会出现if从句,如果复杂的话需要自定义函数)
关键:
1.自定义函数判断IP地址某部分是否有效(即是否符合题目要求)
2.如何截取字符串s的各种子串:substr()函数
3.如何实现剪枝(具体看代码):三处--两处是特殊情况的单独处理,一处是循环遍历对终止条件的缩小
4.终止条件是什么:递归遍历完整个字符串的同时,IP地址恰好被分为4个部分
想清楚上边四点,这道题也就好解决了,剩下的就跟昨天 131. 分割回文串 一个道理。
代码如下:
class Solution {
public: vector<string> ans; vector<string> vec;bool isRange(string substring) { //判断字符串是否为有效IP地址的一部分if (substring.size() != 1 && substring[0] == '0') { //前导0无效(如012,023等等)return false; } int num = stoi(substring); //将字符串转化为数字(字符串只包含数字,不考虑负数)return num <= 255; } void backtrack(string& s, int start) { if (vec.size() == 4 && start == s.size()) { //终止条件:当vec中存储了4个部分,并且刚好遍历完了整个字符串s时,说明找到了一个有效的IP地址string ip = ""; for (int i = 0; i < vec.size(); ++i) { //vec每一部分结束后添加.(最终结果存放在ip里)ip += vec[i]; if (i < vec.size() - 1) { ip += "."; } } ans.push_back(ip); return; } if (start == s.size() && vec.size() != 4) { //剪枝1:当遍历完了整个s但IP地址部分数不为4时,重新返回递归return;}for (int i = start; i < start + 3 && i < s.size(); i++) { //剪枝2:i < start + 3表示IP地址每一部分不超过三位数string substring = s.substr(start, i - start + 1); //截取字符串start到i的子串if (!isRange(substring)) { continue;} vec.push_back(substring); backtrack(s, i + 1); vec.pop_back(); } } vector<string> restoreIpAddresses(string s) { if (s.size() < 4 || s.size() > 12) { //剪枝3:不可能存在有效IP地址情况直接返回空向量return ans;}backtrack(s, 0); return ans; }
};题目二:78.子集
题目链接
78. 子集 - 力扣(LeetCode)
给你一个整数数组
nums,数组中的元素 互不相同 。返回该数组所有可能的子集
(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]示例 2:
输入:nums = [0] 输出:[[],[0]]提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
题解:回溯--子集问题
子集问题个人感觉跟组合问题差不多,可能最大的不同就在于终止条件那里。
这里我们需要注意了,对于对于子集问题:当我们要得到一个数组集合的全部子集,其实是没有终止条件的(当然,你也可以想成有,就是全部都自然遍历添加完,不过这其实跟没有也没区别),也就是说,我们只需要把每一个递归得到的数组添加到结果里边去即可。这里就要求我们对模板的有效运用了,不要没有终止条件就硬想半天。
代码如下:
class Solution {
public:vector<vector<int>> ans;vector<int> vec;void backtrack(vector<int>& nums, int start) {ans.push_back(vec); //注意:所有子集都要添加,没有终止条件限制 for (int i = start; i < nums.size(); i++) {vec.push_back(nums[i]);backtrack(nums, i + 1);vec.pop_back();} }vector<vector<int>> subsets(vector<int>& nums) {backtrack(nums, 0);return ans;}
};
题目三:90.子集II
题目链接
给你一个整数数组
nums,其中可能包含重复元素,请你返回该数组所有可能的子集
(幂集)。解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]示例 2:
输入:nums = [0] 输出:[[],[0]]提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10
题解:回溯--子集问题
这个题算是上面那道的进化版吧,不过思路也差不多,只是数组里出现了重复元素,而要求结果中不能出现重复子集--这不就和昨天打卡不能出现重复组合一样了:对数组排序 + 跳过数组相邻相同的元素(横向同层处理使结果不出现重复子集)。
不理解的话,可以看看昨天的打卡内容,这里就不做分析了。
代码如下:
class Solution {
public:vector<vector<int>> ans;vector<int> vec;void backtrack(vector<int>& nums, int start) {ans.push_back(vec);for (int i = start; i < nums.size(); i++) {if (i > start && nums[i] == nums[i - 1]) { //横向去重:用以跳过同一树层使用过的(重复)元素continue; //注意这里是continue而不是break(break会直接跳出循环,这样一旦出现重复元素,会完全停止遍历剩余的元素,这会导致生成的子集不完整)}vec.push_back(nums[i]);backtrack(nums, i + 1);vec.pop_back();}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end()); //先排序,这样重复的元素就会相邻backtrack(nums, 0);return ans;}
};三、小结
今天的打卡就到此结束了,后边也会继续加油。最后,我是算法小白,但也希望终有所获。
相关文章:

【代码随想录训练营第42期 Day24打卡 回溯Part3 - LeetCode 93.复原IP地址 78.子集 90.子集II
目录 一、做题心得 二、题目与题解 题目一:93.复原IP地址 题目链接 题解:回溯--分割问题 题目二:78.子集 题目链接 题解:回溯--子集问题 题目三:90.子集II 题目链接 题解:回溯--子集问题 三、小…...

python venv和virtualenv详解
一、venv简介 C:\Users\love1>python -m venv -h usage: venv [-h] [--system-site-packages] [--symlinks | --copies] [--clear] [--upgrade] [--without-pip][--prompt PROMPT] [--upgrade-deps]ENV_DIR [ENV_DIR ...]该命令用于在一个目录或者多个目录中创建一个虚拟的…...
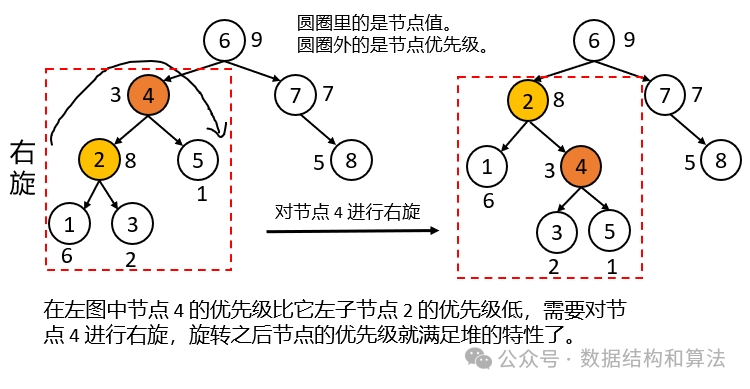
《征服数据结构》树堆(Treap)
摘要: 1,Treap的介绍 2,Treap节点的插入 3,Treap节点的删除 4,Treap和笛卡尔树的区别 1,Treap的介绍 Treap又叫树堆,属于一种自平衡二叉搜索树,是由单词Tree和Heap构成,是…...

论文笔记:OneBit: Towards Extremely Low-bit Large Language Models
202402 arxiv 1 背景 模型量化主要通过把模型的线性层【nn.Linear】(Embedding 层和 Lm_head 层除外)转化为低精度表示实现空间压缩 此前工作的基础是利用 Round-To-Nearest(RTN)方法把高精度浮点数近似映射到附近的整数网格然而…...
)
英语文化中的音乐分类及其发展历史(Classical、Jazz、Rock、Pop、Electronic、Country、RB、Hip-Hop)
文章目录 英语文化中的音乐分类及其发展历史1. 简介2. 古典音乐 (Classical Music)2.1 起源与发展2.2 技术与风格 3. 爵士音乐 (Jazz Music)3.1 起源与发展3.2 技术与风格 4. 摇滚音乐 (Rock Music)(Rock and roll)4.1 起源与发展4.2 技术与风格 5. 蓝调…...
C语言-栈、队列、二叉树
12 栈、队列、二叉树 目录 12 栈、队列、二叉树 一、栈、队列、二叉树是什么? 二、栈 1. 特点:先进后出 -- 有底的盒子 2. 使用场景:函数调用 -- 中断机制 3. 实现栈的形式: 三、队列 1. 特点:先进先出 -- 水…...
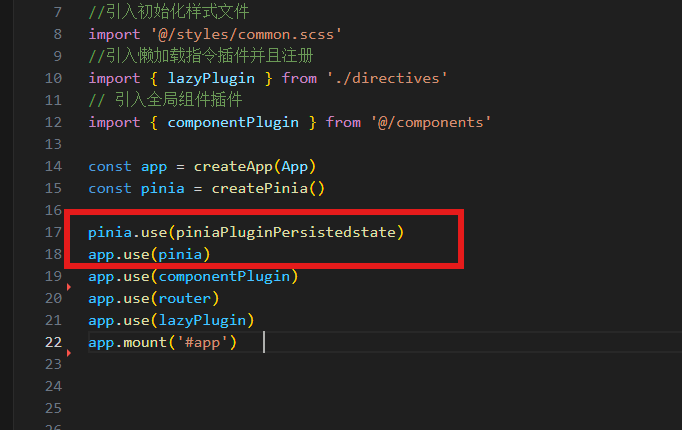
pinia-plugin-persistedstate 插件不生效
引入使用该插件使用时发现不生效 原因:pinia实例调用顺序不当 将: // import ./assets/main.css import { createApp } from vue import { createPinia } from pinia import piniaPluginPersistedstate from pinia-plugin-persistedstate import App fr…...

sqlite 合并两个数据库中的特定表
sqlite 合并两个数据库中的特定表 命令行python 版本 命令行 .open v1/mydb.db attach v2/mydb.db as db2; insert into main.表1 select * from db2.表1; insert into main.表2 select * from db2.表2; .exit参数说明v1/mydb.db主db文件路径,合并后的结果就是它…...

winform中设置DateTimePicker参数为空
在C#中,使用DateTimePicker控件时,您可以将其Value属性设置为null或者DateTime.MinValue来表示没有选定的日期或时间。以下是如何设置默认值为空的示例代码: dateTimePicker1.Value DateTime.MinValue; 或者,如果您希望用户不能…...
)
Python爬虫(8)
JsonPath介绍使用 JsonPath是一种轻量级的查询库,可以从JSON文本数据中进行筛选和提取操作。有点类似于使用XPath在HTML数据中提取数据的功能。JsonPath 也可以通过使用类似于 XPath 的表达式来访问 JSON对象中的属性和元素,并支持通配符、筛选器和函数…...

靓图!多点创新!CEEMDAN-Kmeans-VMD-CNN-LSTM-Attention双重分解+卷积长短期+注意力多元时间序列预测
靓图!多点创新!CEEMDAN-Kmeans-VMD-CNN-LSTM-Attention双重分解卷积长短期注意力多元时间序列预测 目录 靓图!多点创新!CEEMDAN-Kmeans-VMD-CNN-LSTM-Attention双重分解卷积长短期注意力多元时间序列预测效果一览基本介绍程序设计…...

zdpgo_gin_limit 为zdpgo_gin打造的接口限流框架,当API接口需要限制访问频率的时候可以使用此框架
zdpgo_gin_limit 为zdpgo_gin打造的接口限流框架,当API接口需要限制访问频率的时候可以使用此框架 安装 go get github.com/zhangdapeng520/zdpgo_gin_limit使用教程 基于内存的限流 package mainimport (gin "github.com/zhangdapeng520/zdpgo_gin"…...

Java1234的Vue学习笔记
第一节 vue.js简介 简介 第二节 vue开发工具 vscode 第三节:vue HelloWorld实现 理解vue双向绑定v-model的概念 底层数据改变视图对应显示会变,视图绑定数据变会影响底层数据,对应MVVM模式http://blog.java1234.com/blog/articles/510.html <!DOCTYPE html> <…...
)
嵌入式八股-C++面试91题(20240809)
1. 讲一讲封装、继承、多态是什么? 封装:将具体实现过程和数据封装成一个类,只能通过接口进行访问,降低耦合性,使类成为一个具有内部数据的自我隐藏能力、功能独立的软件模块。 意义:保护代码防止被破坏&…...
如何恢复误删视频?找回误删视频文件的办法分享
在数字化时代,视频已成为我们生活中不可或缺的一部分,记录着珍贵的回忆、工作资料或是学习素材。然而,在电脑上一不小心误删视频文件,该怎么办?视频误删怎么恢复?有什么小技巧可以找回删除的视频࿱…...

游戏手柄开发一款游戏
使用游戏手柄开发一款游戏是一个既有趣又充满挑战的项目。这通常涉及多个步骤,包括选择合适的硬件、学习编程技能、设计游戏逻辑以及测试和优化游戏。以下是一个大致的步骤指南,帮助你开始这个过程: 1. 确定游戏类型和概念 游戏类型&#x…...
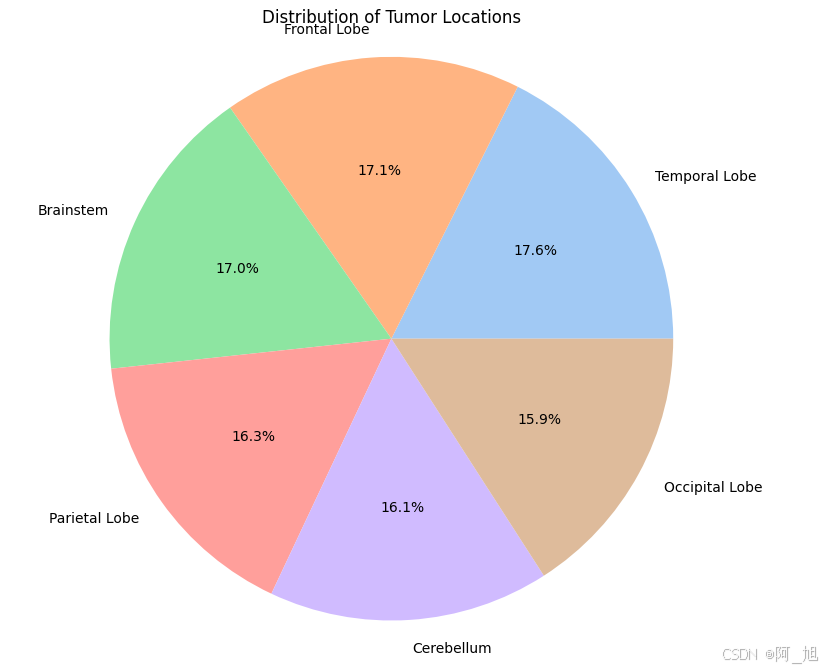
【阿旭机器学习实战】【39】脑肿瘤数据分析与预测案例:数据分析、预处理、模型训练预测、评估
《------往期经典推荐------》 一、【100个深度学习实战项目】【链接】,持续更新~~ 二、机器学习实战专栏【链接】,已更新31期,欢迎关注,持续更新中~~ 三、深度学习【Pytorch】专栏【链接】 四、【Stable Diffusion绘画系列】专…...

深度学习基础 - 梯度垂直于等高线的切线
深度学习基础 - 梯度垂直于等高线的切线 flyfish 梯度 给定一个标量函数 f ( x , y ) f(x, y) f(x,y),它的梯度(gradient)是一个向量,表示为 ∇ f ( x , y ) \nabla f(x, y) ∇f(x,y),定义为: ∇ f ( x…...

py2exe打包
要用到py2exe打包python程序,记录一下。 写一个setup.py文件,内容如下: from distutils.core import setup import py2exeoptions {"py2exe":{"compressed": 1, # 0或1 1压缩,0不压缩"optimize&quo…...

Gerrit存在两个未审核提交且这两个提交有冲突时的解决方案
Gerrit存在两个未审核提交且这两个提交有冲突时的解决方案 问题背景 用户A提交了一个记录,用户A的记录未审核此时用户B又提交了,这个时候管理员去合并代码,合了其中一个后再去合另一个发现合并不了,提示冲突,这个时候另…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
