同态加密和SEAL库的介绍(六)BGV 方案
前面介绍 BFV 和 CKKS 加密方案,这两者更为常用。并且也解释了 Batch Encoder 和 级别的概念,这对接下来演示 BGV 会很有帮助。
一、BGV简介
BGV (Brakerski-Gentry-Vaikuntanathan) 方案 是一种基于环学习同态加密(RLWE)问题的加密方案。BGV 方案可以实现任意计算电路的同态加密,特别适合于加密数据的复杂运算。
特点:
- 同态运算:支持加法和乘法的任意组合,这意味着它可以评估任意计算电路。
- 级联密文:密文可以通过一系列同态运算来处理,而不需要在每一步进行解密和重新加密。
- 噪声管理:在每次同态运算之后,密文中的噪声会增加。BGV 方案采用了噪声管理技术(例如重新线性化和模数切换)来控制噪声增长,确保运算的正确性。
优点:
- 灵活性:支持任意复杂的计算。
- 效率:通过噪声管理技术提高了运算效率。
- 安全性:基于环学习同态加密问题的安全性高。
缺点:
- 复杂性:实现和使用BGV方案比一些其他方案更为复杂。
- 资源消耗:噪声管理和重新线性化等操作增加了计算和存储的开销。
二、3种方案比较:
先看发展顺序:
- BGV 方案:2011年 Brakerski、Gentry 和 Vaikuntanathan 提出。
- BFV 方案:2012年 Fan 和 Vercauteren 提出。
- CKKS 方案:2017年 Cheon、Kim、Kim 和 Song 提出。
分别的适用场景:
- 如果需要对整数进行精确计算,BFV 方案是一个好的选择。
- 如果需要对浮点数进行近似计算,CKKS 方案是更合适的。
- 如果需要复杂的计算电路,BGV 方案提供了最大的灵活性。
每种方案都有其独特的优势和适用场景,在实际应用中,选择适合的方案可以最大化地发挥同态加密技术的优势。
三、BGV 示例
在本示例中,计算8次多项式 ,并且在整数 1、2、3、4上的加密
。多项式的系数可以看作是明文输入计算在 plain_modulus == 1032193 模数下进行。
在BGV方案中对加密数据进行计算类似于BFV。这个例子的主要目的是解释BFV和BGV在密文系数模数选择和噪声控制方面的区别。
3.1 参数设置和创建实例
这里先使用 BFVDefault 创建 coeff_modulus,后面会介绍如何更好的设置。
EncryptionParameters parms(scheme_type::bgv);
size_t poly_modulus_degree = 8192;
parms.set_poly_modulus_degree(poly_modulus_degree);
parms.set_coeff_modulus(CoeffModulus::BFVDefault(poly_modulus_degree));
parms.set_plain_modulus(PlainModulus::Batching(poly_modulus_degree, 20));
SEALContext context(parms);KeyGenerator keygen(context);
SecretKey secret_key = keygen.secret_key();
PublicKey public_key;
keygen.create_public_key(public_key);
RelinKeys relin_keys;
keygen.create_relin_keys(relin_keys);
Encryptor encryptor(context, public_key);
Evaluator evaluator(context);
Decryptor decryptor(context, secret_key); 这里想再次强调一下,因为用的是 Batch 批处理,所以在设置 plain_modulus 的时候,要求是与 2倍 poly_modulus_degree 同余 1 的素数,这与普通的 Encoder 要求不同。上面代码中是用 PlainModulus::Batching 自动生成满足条件的随机数。
这里输出设置的参数:

3.2 设置输入并编码
批处理和槽操作在 BFV 和 BGV 中是相同的:
BatchEncoder batch_encoder(context);
size_t slot_count = batch_encoder.slot_count();
size_t row_size = slot_count / 2; 这里特意设置 row_size 变量,是因为之前讲批处理的时候,强调过内部在逻辑上会编码成两行,故其实就是 。当然这个结构对于编码和计算是基本无感的,只有在考虑行旋转和列旋转的时候会有影响,这个下一篇会具体介绍(挖坑 + 1)。
vector<uint64_t> pod_matrix(slot_count, 0ULL);
pod_matrix[0] = 1ULL;
pod_matrix[1] = 2ULL;
pod_matrix[2] = 3ULL;
pod_matrix[3] = 4ULL;
Plaintext x_plain;
batch_encoder.encode(pod_matrix, x_plain);这里对编码结果打印输出一下:

3.3 直接运算
Ciphertext x_encrypted;
cout << "Encrypt x_plain to x_encrypted." << endl;
encryptor.encrypt(x_plain, x_encrypted);
cout << "+ noise budget in freshly encrypted x: " << decryptor.invariant_noise_budget(x_encrypted) << " bits" << endl;这里先对输入进行加密,并输出噪声预算:

先计算 :
Ciphertext x_squared;
evaluator.square(x_encrypted, x_squared);
cout << "+ size of x_squared: " << x_squared.size() << endl;
evaluator.relinearize_inplace(x_squared, relin_keys);
cout << "+ size of x_squared (after relinearization): " << x_squared.size() << endl;
cout << "+ noise budget in x_squared: " << decryptor.invariant_noise_budget(x_squared) << " bits" << endl;因为是 密文乘密文,为了减少乘法后的密文大小,这里进行了重新线性化,并输出了噪声预算,同时进行解密验证:

可以看出,运算中间结果是正确的,并且重新线性化后,密文大小从3减小到2。
再计算 :
Ciphertext x_4th;
evaluator.square(x_squared, x_4th);
cout << "+ size of x_4th: " << x_4th.size() << endl;
evaluator.relinearize_inplace(x_4th, relin_keys);
cout << "+ size of x_4th (after relinearization): " << x_4th.size() << endl;
cout << "+ noise budget in x_4th: " << decryptor.invariant_noise_budget(x_4th) << " bits" << endl;同样进行了重新线性化,并输出目前噪声预算,同时进行解密验证:

可以看出这里的噪声预算下降的特别快,只剩 35 bits 了。
最后计算 :
Ciphertext x_8th;
evaluator.square(x_4th, x_8th);
cout << "+ size of x_8th: " << x_8th.size() << endl;
evaluator.relinearize_inplace(x_8th, relin_keys);
cout << "+ size of x_8th (after relinearization): " << x_8th.size() << endl;
cout << "+ noise budget in x_8th: " << decryptor.invariant_noise_budget(x_8th) << " bits" << endl;
噪声预算已经达到0,这意味着解密无法得到正确的结果。故此,引出 BGV需要模数切换以减少噪声增长!
3.4 加入模数切换的运算
下面演示在每次重新线性化后插入模数切换:(避免啰嗦,这里直接完整计算)
cout << "+ noise budget in x_squared (previously): " << decryptor.invariant_noise_budget(x_squared) << " bits" << endl;
evaluator.square(x_encrypted, x_squared);
evaluator.relinearize_inplace(x_squared, relin_keys);
evaluator.mod_switch_to_next_inplace(x_squared);
cout << "+ noise budget in x_squared (with modulus switching): " << decryptor.invariant_noise_budget(x_squared) << " bits" << endl;evaluator.square(x_squared, x_4th);
evaluator.relinearize_inplace(x_4th, relin_keys);
evaluator.mod_switch_to_next_inplace(x_4th);
cout << "+ noise budget in x_4th (with modulus switching): " << decryptor.invariant_noise_budget(x_4th) << " bits" << endl;evaluator.square(x_4th, x_8th);
evaluator.relinearize_inplace(x_8th, relin_keys);
evaluator.mod_switch_to_next_inplace(x_8th);
cout << "+ noise budget in x_8th (with modulus switching): " << decryptor.invariant_noise_budget(x_8th) << " bits" << endl;decryptor.decrypt(x_8th, decrypted_result);
batch_encoder.decode(decrypted_result, pod_result);这里对中间结果也进行解密,并输出其噪声预算的变化:

这里仔细对比可以发现:虽然通过模数切换 x_squared 的噪声预算比之前少,但噪声预算的消耗速率较慢,故最后可以正确解密。
四、总结
通过之前的介绍实验,我们能发现,有时候进行模数切换会损耗噪声预算,但是进行到一定乘法深度后,再进行切换就不会损耗噪声,这种情况是一定适合加入模数切换的。
同时上面发现虽然降低了 x_squared 的噪声预算,但是噪声预算的消耗减慢,故这种情况也适合加入模数切换。
但是这些不意味着在每次计算后都应该进行模数切换,因为要权衡减少的预算和减缓消耗的速度,最好自己进行实验比对。"故为了在应用中实现噪声预算的最佳消耗速率,需要仔细选择插入模数切换的位置,并手动选择 coeff_modulus。"
下篇介绍对密文进行的 行旋转 和 列旋转(未完待续。。。)
相关文章:

同态加密和SEAL库的介绍(六)BGV 方案
前面介绍 BFV 和 CKKS 加密方案,这两者更为常用。并且也解释了 Batch Encoder 和 级别的概念,这对接下来演示 BGV 会很有帮助。 一、BGV简介 BGV (Brakerski-Gentry-Vaikuntanathan) 方案 是一种基于环学习同态加密(RLWE)问题的加…...

uniapp微信小程序 canvas绘制圆形半透明阴影 createCircularGradient函数不支持透明度部分解决方案
背景 我需要在微信小程序中,用canvas绘制一个圆形钟表,在ui设计图中,有一部分阴影,这里我节选一下: 即深色发黑的部分 canvas通用阴影绘制 由于canvas中并不支持css那样简单的方式为圆形添加阴影或高光,…...

W34KN3SS靶机
信息收集: 靶机地址:https://www.vulnhub.com/entry/w34kn3ss-1,270/# (1)ip扫描 nmap 192.168.254.0/24 -sn | grep -B 2 00:0C:29:E8:66:AB (2)端口扫描 nmap -p- -A 192.168.254.145 (3&…...
8.9套题
A. 猴猴吃苹果 题意:给定根节点k,求访问点的顺序,使得每次从上一个点到当前点的权值最大。访问过的点权值为0。权值一样时,输出最小编号 思路:由于是双向边,先求根节点到每一个节点的距离值。在第一轮中&…...

Python 爬取网页水务数据并实现智慧水务前端可视化
提示:本文爬取深圳市环境水务集团有限公司的公开数据作为数据样例进行数据分析与可视化。 文章目录 一、爬虫二、对爬取的数据进行数据库、excel的存储与数据处理1.代码实现 三、应用Flask框架将后端获取数据后渲染到前端四、前端Echarts的使用1.下载echarts.min.js…...

百度智能云发布3款轻量级+2款场景大模型
文心大模型ERNIE 3.5是目前百度智能云千帆大模型平台上最受欢迎的基础大模型之一。针对用户的常见通用的对话场景,ERNIE 3.5 在指令遵循、上下文学习和逻辑推理能力三方面分别进行了能力增强。 ERNIE Speed作为三款轻量级大模型中的“大个子”,推理场景…...

UE基础 —— 编辑器界面
菜单栏 UE中每个编辑器都有一个菜单栏,部分菜单会出现在所有编辑器窗口中,如File、Window、Help,其他则是其编辑器特有的; 主工具栏 UE中部分最常用的工具和命令的快捷方式; 1,保存按钮(ctrls&a…...
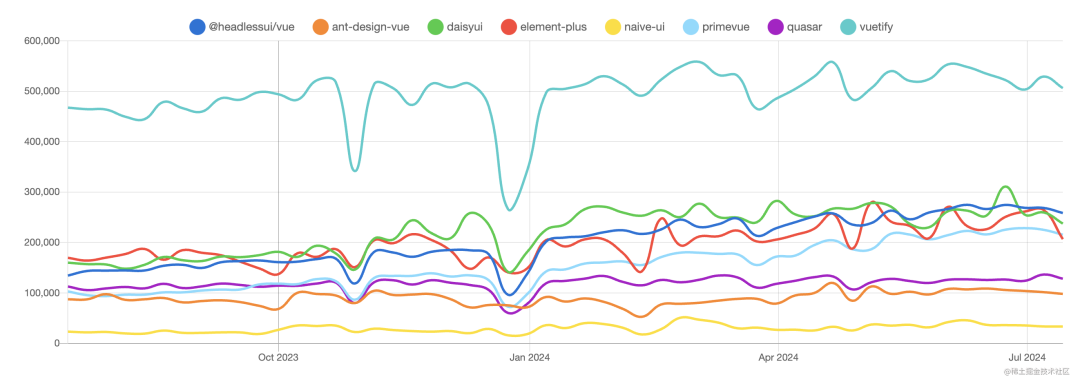
2024年Vue组件库大比拼:谁将成为下一个Element?
2024 年,Vue生态蓬勃发展,越来越多的开发者开始探索更适合自己项目的组件库。 今天我们来看一下2024年最受欢迎的几款Vue开源组件库,除了Element,开发者们还有哪些选择呢? 1.Vuetify Vuetify是由社区支持的Vue组件库&…...

SS9283403 sqlite3交叉编译并部署到SS928(六)
1.Sqlite3下载 连接:SQLite Download Page 2.解压 tar zxvf sqlite-autoconf-3460000.tar.gz 3.配置并编译 进入解压目录,打开命令行,输入如下命令 ./configure CCaarch64-mix210-linux-gcc --hostarm-linux --prefix/home/mc/work/sqlite…...

java3d-1_4_0_01-windows-i586.exe
下载 Java 3D API 安装 C:\Program Files\Java\Java3D\1.4.0_01\bin C:\Java\jre6 C:\Java\jdk1.6.0_45 C:\Windows 记录下这 4 个目录,去检查下 4 哥目录下文件多了什么 检查目录① C:\Program Files\Java\Java3D\1.4.0_01\bin 检查目录② C:\Java\jre6 C:…...

Vue3中的history模式路由:打造无缝导航体验!
Hey小伙伴们,今天给大家带来Vue3中使用history模式路由的实战案例!🌟 🔍 项目背景 Vue3的路由功能非常强大,可以帮助我们轻松实现单页面应用中的页面切换。但是你知道吗?默认情况下Vue Router使用的是has…...

python(6)
一、datetime函数 方法一: 前一个datetime是模块。后一个datetime是类型 方法二: 方法三: 二、逆序字符串 三 、旋转字符串...

以Zed项目为例学习大型Rust项目的组织与管理
说明 Zed项目代码:https://github.com/zed-industries/zed.git本文项目代码:https://github.com/VinciYan/zed_workspace.git Zed是一款由Atom创始人开发的高性能、协作友好的现代开源代码编辑器,使用Rust编写,集成AI辅助功能&a…...

正点原子imx6ull-mini-Linux驱动之Linux RS232/485/GPS 驱动实验(23)
错误1:我一直找不到为什么我的minicom用不了,编译啥的都通过了,原来是我的密码文件命名错了,我就习以为常的命名为password,谁知道应该是passwd,所以以后该复制的还是复制,不然就容易找不到源头…...
用户上下文打通+本地缓存Guava
文章目录 🌞 Sun Frame:SpringBoot 的轻量级开发框架(个人开源项目推荐)🌟 亮点功能📦 spring cloud模块概览常用工具 🔗 更多信息1.设计1.链路流程2.详细设计 2.网关过滤器获取唯一标识放到Hea…...
-MFC-C/C++ - 树形视图(Tree Control) - CTreeCtrl)
Windows图形界面(GUI)-MFC-C/C++ - 树形视图(Tree Control) - CTreeCtrl
公开视频 -> 链接点击跳转公开课程博客首页 -> 链接点击跳转博客主页 目录 树形视图(Tree Control) - CTreeCtrl 创建和初始化 添加和删除项 获取和设置项属性 操作项 项选择变化 项双击 项展开 示例代码 树形视图(Tree Control) - CTreeCtrl 创建和初始…...

C语言 --- 枚举、位运算
(一)枚举 1.概念:枚举是指将变量的值一一列举出来,变量的值只限于列举出来的值的范围 2.作用:a.提高代码可读性;b.提高代码的安全性 3.枚举类型: enum 枚举名 { 列举各种值 //枚举元素或枚…...

12322222222
当您和老王不在同一个网段时,您们之间的通信需要通过路由器来实现。这是因为不同的网段被视为不同的网络,而路由器的作用之一就是连接不同的网络并负责数据包的转发。下面是详细的通信流程: 本地网络通信尝试:您的设备࿰…...

知识改变命运:Java 语言 【可变参数】
可变参数 概念:Java允许一个类中多个同名同功能但是参数不同的方法,封装为一个方法。 基本语法: 访问修饰符 返回值 方法名 (数据类型...参数名) { ...... }案例:写一个类名DyMethod 方法名sum 计算两个整数和,三个整…...

Spring及相关框架的重要的问题
Java框架 问题一:Spring框架中的单例bean是线程安全的吗? 看下图,不能被修改的成员变量就是无状态的类,无状态的类没有线程安全问题,所以在开发中尽量避免可修改的成员变量。 回答:不是线程安全的…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
