“二分”带来“十分”快感——二分思想的奥秘解析
文章目录
- 无处不在的二分思想
- 二分查找惊人的查找速度
- 二分查找的递归与非递归实现
- 1.循环退出条件
- 2.mid的取值
- 3.low和high的更新
- 最后说一句

🐱🐉作者简介:大家好,我是黑洞晓威,一名大二学生,希望和大家一起进步。
👿本文收录于 算法,本专栏是针对大学生、初学算法的人准备,解析常见的数据结构与算法,同时备战蓝桥杯。
无处不在的二分思想
二分查找是一种非常简单易懂的快速查找算法,生活中到处可见。比如说,我们现在来做一个猜字游戏。我随机写一个0到99之间的数字,然后你来猜我写的是什么。猜的过程中,你每猜一次,我就会告诉你猜的大了还是小了,直到猜中为止。你来想想,如何快速猜中我写的数字呢?
假设我写的数字是23,你可以按照下面的步骤来试一试。(如果猜测范围的数字有偶数个,中间数有两个,就选择较小的那个。)

7次就猜出来了,是不是很快?这个例子用的就是二分思想,按照这个思想,即便我让你猜的是0到999的数字,最多也只要10次就能猜中。不信的话,你可以试一试。

看懂这两个例子,你现在对二分的思想应该掌握得妥妥的了。我这里稍微总结升华一下, 二分查找针对的是一个有序的数据集合,查找思想有点类似分治思想。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为0。
二分查找惊人的查找速度
二分查找是一种非常高效的查找算法,高效到什么程度呢?我们来分析一下它的时间复杂度。
我们假设数据大小是n,每次查找后数据都会缩小为原来的一半,也就是会除以2。最坏情况下,直到查找区间被缩小为空,才停止。

可以看出来,这是一个等比数列。其中n/2k=1时,k的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较,所以,经过了k次区间缩小操作,时间复杂度就是O(k)。通过n/2k=1,我们可以求得k=log2n,所以时间复杂度就是O(logn)。
因为logn是一个非常“恐怖”的数量级,即便n非常非常大,对应的logn也很小。比如n等于2的32次方,这个数很大了吧?大约是42亿。也就是说,如果我们在42亿个数据中用二分查找一个数据,最多需要比较32次。
二分查找的递归与非递归实现
实际上,简单的二分查找并不难写,注意我这里的“简单”二字。讲到二分查找的变体问题,那才是真正烧脑的。今天,我们来看如何来写最简单的二分查找。
最简单的情况 就是 有序数组中不存在重复元素,我们在其中用二分查找值等于给定值的数据。我用Java代码实现了一个最简单的二分查找算法。
public int bsearch(int[] a, int n, int value) {int low = 0;int high = n - 1;while (low <= high) {int mid = (low + high) / 2;if (a[mid] == value) {return mid;} else if (a[mid] < value) {low = mid + 1;} else {high = mid - 1;}}return -1;
}这个代码我稍微解释一下,low、high、mid都是指数组下标,其中low和high表示当前查找的区间范围,初始low=0, high=n-1。mid表示[low, high]的中间位置。我们通过对比a[mid]与value的大小,来更新接下来要查找的区间范围,直到找到或者区间缩小为0,就退出。如果你有一些编程基础,看懂这些应该不成问题。现在,我就着重强调一下 容易出错的3个地方。
1.循环退出条件
注意是low<=high,而不是low<high。
2.mid的取值
实际上,mid=(low+high)/2这种写法是有问题的。因为如果low和high比较大的话,两者之和就有可能会溢出。改进的方法是将mid的计算方式写成low+(high-low)/2。更进一步,如果要将性能优化到极致的话,我们可以将这里的除以2操作转化成位运算low+((high-low)>>1)。因为相比除法运算来说,计算机处理位运算要快得多。
3.low和high的更新
low=mid+1,high=mid-1。注意这里的+1和-1,如果直接写成low=mid或者high=mid,就可能会发生死循环。比如,当high=3,low=3时,如果a[3]不等于value,就会导致一直循环不退出。
如果你留意我刚讲的这三点,我想一个简单的二分查找你已经可以实现了。 实际上,二分查找除了用循环来实现,还可以用递归来实现,过程也非常简单。
我用Java语言实现了一下这个过程,正好你可以借此机会回顾一下写递归代码的技巧。
// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {return bsearchInternally(a, 0, n - 1, val);
}private int bsearchInternally(int[] a, int low, int high, int value) {if (low > high) return -1;int mid = low + ((high - low) >> 1);if (a[mid] == value) {return mid;} else if (a[mid] < value) {return bsearchInternally(a, mid+1, high, value);} else {return bsearchInternally(a, low, mid-1, value);}
}最后说一句
感谢大家的阅读,文章通过网络资源与自己的学习过程整理出来,希望能帮助到大家。
才疏学浅,难免会有纰漏,如果你发现了错误的地方,可以提出来,我会对其加以修改。

相关文章:

“二分”带来“十分”快感——二分思想的奥秘解析
文章目录无处不在的二分思想二分查找惊人的查找速度二分查找的递归与非递归实现1.循环退出条件2.mid的取值3.low和high的更新最后说一句🐱🐉作者简介:大家好,我是黑洞晓威,一名大二学生,希望和大家一起进…...

一台服务器最大能支持多少条 TCP 连接?问倒一大片。。。
一台服务器最大能打开的文件数 限制参数 我们知道在Linux中一切皆文件,那么一台服务器最大能打开多少个文件呢?Linux上能打开的最大文件数量受三个参数影响,分别是: fs.file-max (系统级别参数)…...
蓝桥杯嵌入式RTC实时时钟
文章目录 前言一、RTC是什么二、cubemx的配置三、函数的使用总结前言 本篇文章将给大家介绍RTC实时时钟。 一、RTC是什么 STM32的实时时钟RTC是一个独立的定时器,RTC时钟内部依靠BCD码计数。RTC实时时钟提高时钟、闹钟、日历功能。RTC功耗较低,可以使用在低功耗设备上。 …...
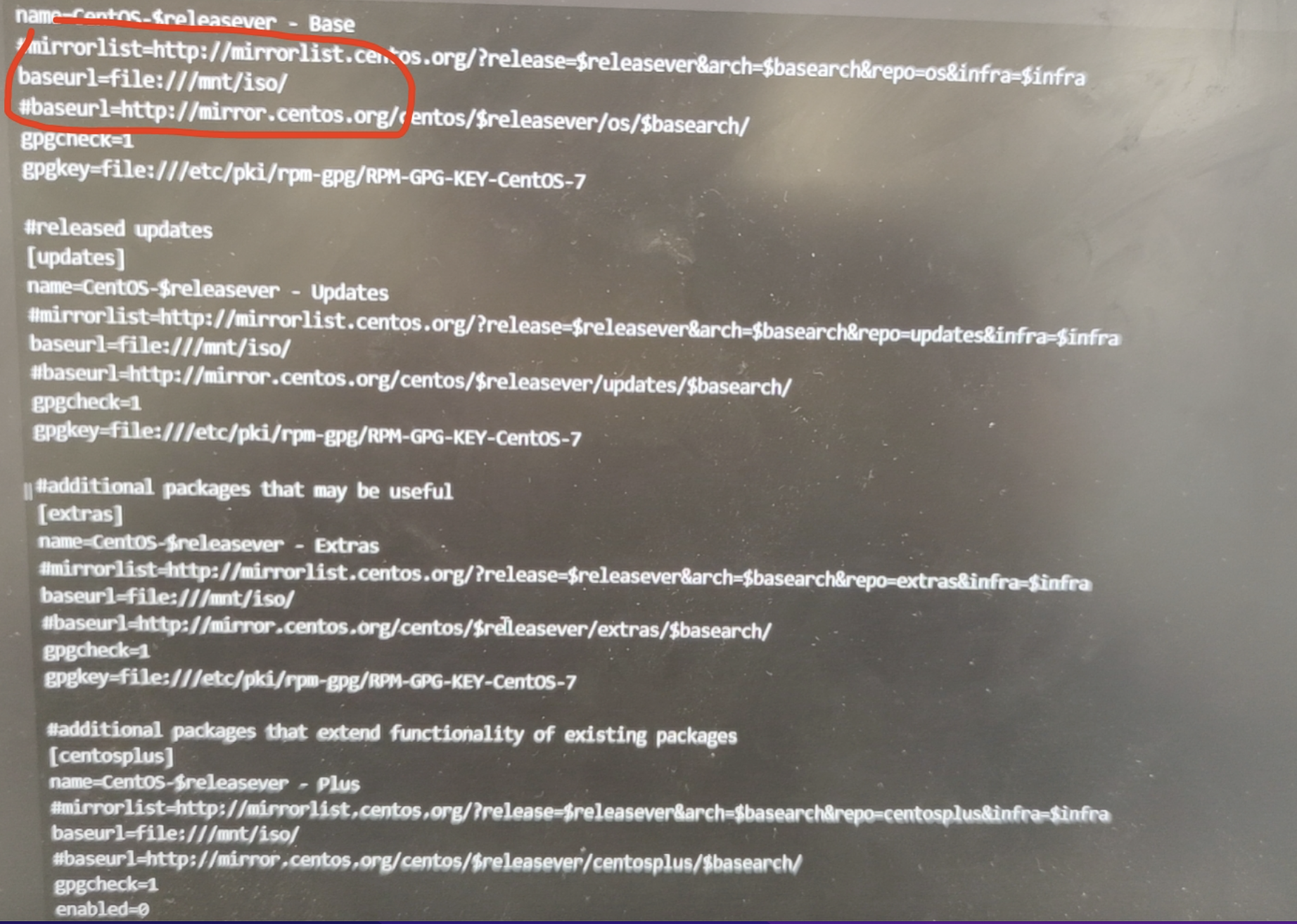
Centos7 挂载 ISO镜像
切到mnt目录:cd /mnt mkdir iso确保centos镜像在服务上存在,磁盘挂载mount -o loop /home/xx.iso /mnt/iso查看是否挂载成功df -h出现红色的部分表示挂载成功修改源切目录并修改yum源:cd /etc/yum.repos.dllvim Centos-Base.repo修改后yum clean allyum list安装lrz…...

三级数据库备考--数据库应用系统开发方法第一次练习(刷题库知识点记录)
1.数据库的三级模式由外模式、模式、内模式构成。外模式是用户可见的部分数据的存在形式;模式可以等价为全体数据的逻辑结构且用户不可见,是三级模式的中间部分;内模式对应数据库的物理结构和存储方式。当模式改变时,由数据库管理…...

免费空间主机是什么?怎么申请免费空间主机
随着网络的普及,越来越多的人开始使用免费空间。这种新的商业模式也让一些商家得以获利。 1:免费空间的概念 免费空间是指允许您自由使用的网络服务。这意味着它可以被任何人用来创建、编辑和发布网站内容或应用程序,而无需考虑任何付费业务协…...
)
网络安全文章汇总导航(持续更新)
网络安全文章汇总导航(持续更新)1.基础篇(已完结):2.工具篇(持续更新):3.靶场安装(持续更新,但不确定):4.权限提升(持续更…...

AI-TestOps —— 软件测试工程师的一把利剑
写在前面软件测试的前世今生测试工具开始盛行AI-TestOps 云平台● AI-TestOps 功能模块● AI-TestOps 自动化测试流程写在前面 最近偶然间看到一句话:“软件测试是整个 IT 行业中最差的岗位”。这顿时激起了我对软件测试领域的兴趣,虽然之前未涉及过软件…...
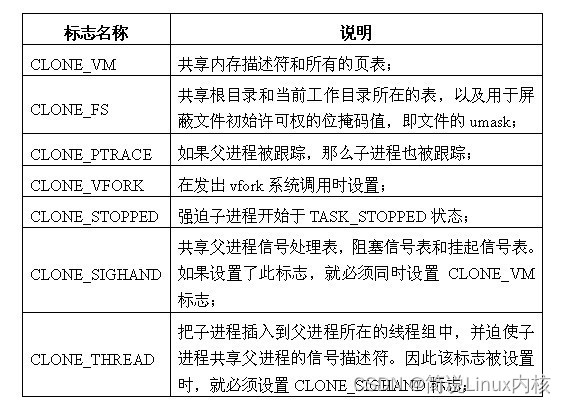
Linux内核进程管理原理详解
前言:Linux内核里大部分都是C语言。建议先看《Linux内核设计与实现(Linux Kernel Development)》,Robert Love,也就是LKD。Linux是一种动态系统,能够适应不断变化的计算需求。Linux计算需求的表现是以进程的通用抽象为中心的。进程可以是短期…...

通过Linux串口实现树莓派与电脑通信
目录 一 串口说明 二 USB—TTL模块 ● usb-ttl模块接口 三 串口通信常用的API 四 修改串口的配置文件 五 串口通信代码验证 ● 发送一个字符/字符串到串口 ● 树莓读取串口数据(字符) ● 代码拓展(双方) 一 串口…...

全球变暖 蓝桥杯 178
题目描述你有一张某海域 NxN 像素的照片,"."表示海洋、"#"表示陆地,如下所示:........##.....##........##...####....###........其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座…...
Java现在好找工作吗?
Java到2023年已经28岁了,可能你会怀疑它是否还一如当年一样的强大,在应用层领域独占鳌头。但是基于Java庞大的市场占有率和需求,它依然在保持着更新迭代,依然是最常用的底层开发语言,基于其安全性、开放性、稳定性和跨…...
Flink 第1章 基础介绍和特性
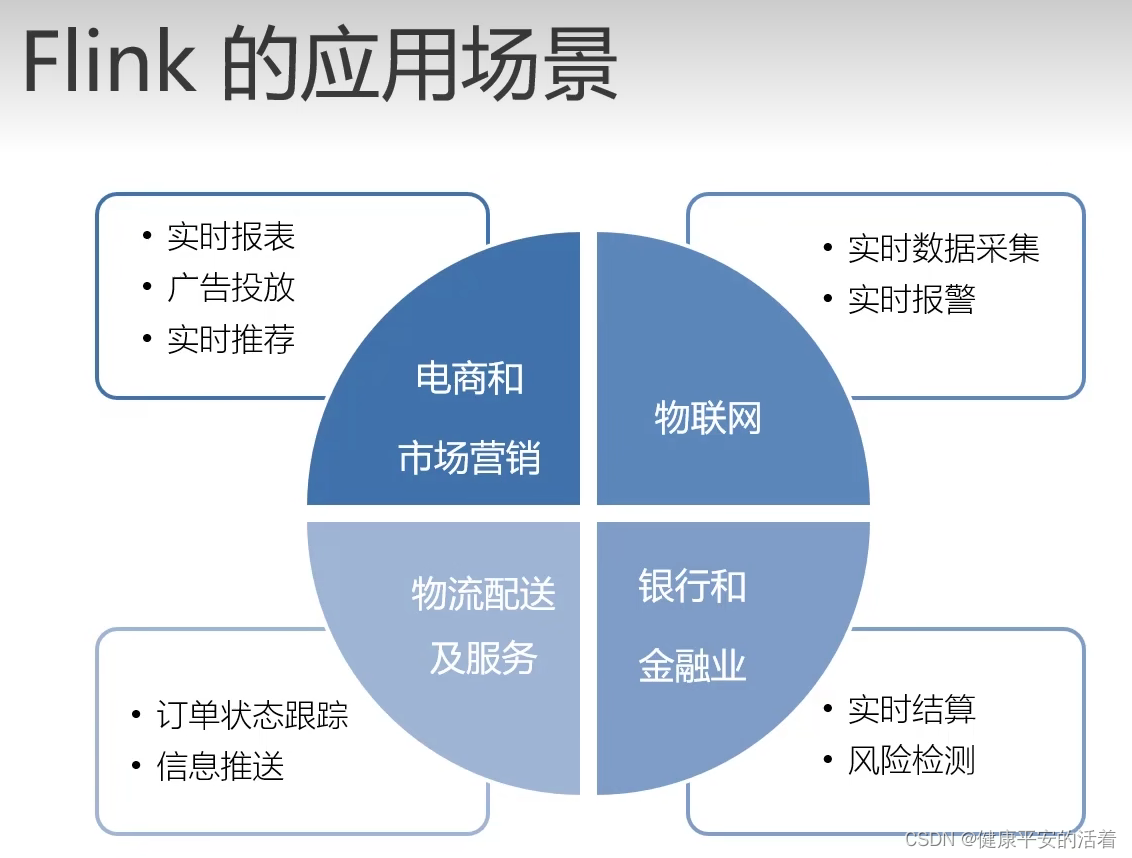
一 Flink概念 1.1 Flink的概念 Flink是一个框架和分布式处理引擎,用于对无界和有解数据流进行状态计算。如下图所示: 1.2 Flink的应用场景 1.3 Flink的目标 1.高吞吐量 2.低延迟 3,结果的准确性和良好的容错性。 1.4 Flink与spark的区别…...

docker 安装 nginx无坑版
一. 拉取镜像 docker pull nginx二. 创建挂载目录 mkdir -p /usr/local/nginx/conf mkdir -p /usr/local/nginx/log mkdir -p /usr/local/nginx/html三. 从nginx容器里复制nginx的配置文件到主机里 创建个容器 docker run --name nginx -p 80:80 -d nginx将容器内的配置文件…...
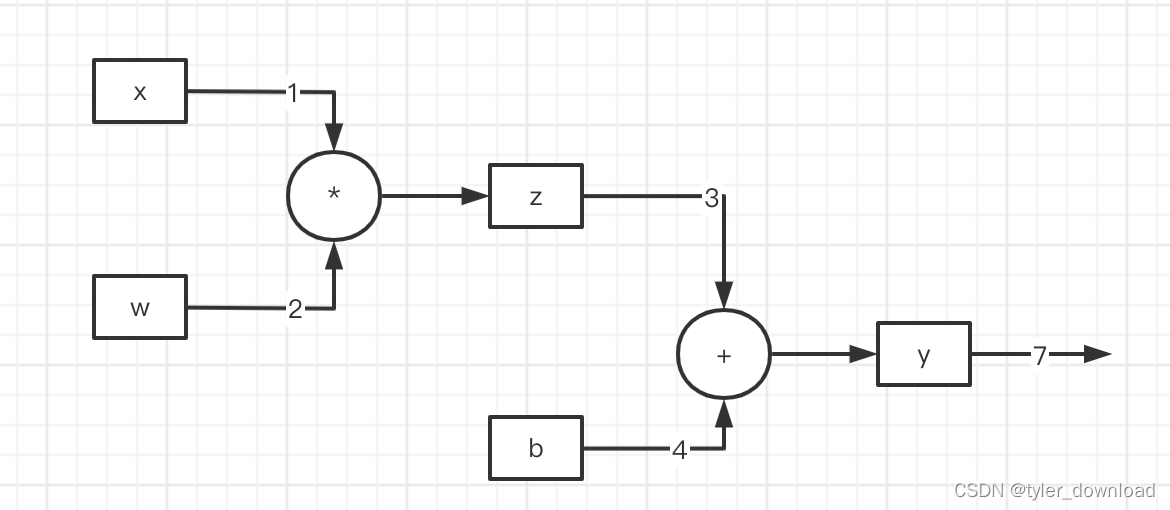
自己动手做chatGPT:向量的概念和相关操作
chatGPT的横空出世给人工智能注入一针强心剂,它是历史上以最短时间达到一亿用户的应用。chatGPT的能力相当惊人,它可以用相当流利的语言和人对话,同时能够对用户提出的问题给出相当顺畅的答案。它的出现已经给各个行业带来不小冲击࿰…...
【洛谷刷题】蓝桥杯专题突破-深度优先搜索-dfs(7)
目录 写在前面: 题目:P1596 [USACO10OCT]Lake Counting S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述: 输入格式: 输出格式: 输入样例: 输出样例: 解题思路: …...

Python嵌套函数(Nested function)和闭包(closure)
Python嵌套函数(Nested function)和闭包(closure) 闭包(closure)是建立在嵌套函数基础上的,是一种特殊的嵌套函数结构。 先看嵌套函数(Nested function)。 Python允许…...
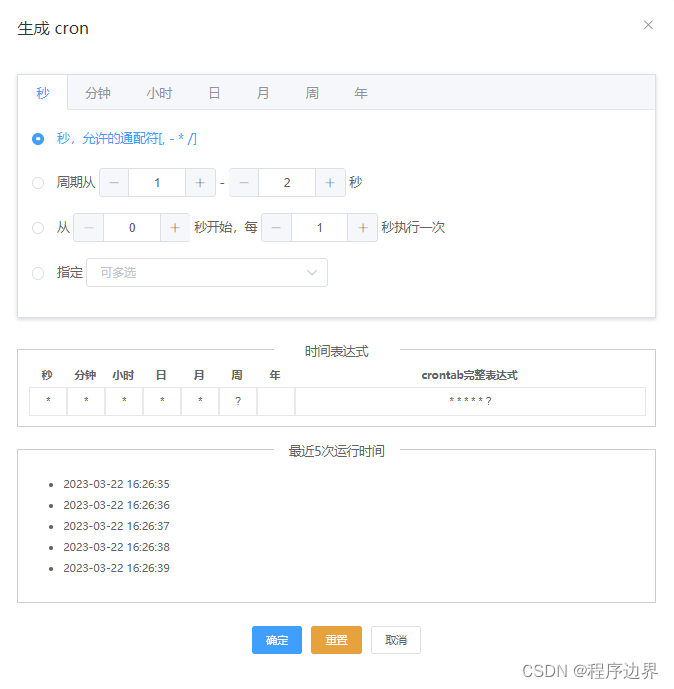
【实战】React 必会第三方插件 —— Cron 表达式生成器(qnn-react-cron)
文章目录一、引子二、配置使用1.安装2.使用(1)直接调用(2)赋值到表单(Form)(3)自定义功能按钮(4)隐藏指定 Tab(5)其他三、常见问题及解…...

C# 教你如何终止Task线程
我们在多线程中通常使用一个bool IsExit类似的代码来控制是否线程的运行与终止,其实使用CancellationTokenSource来进行控制更为好用,下面我们将介绍CancellationTokenSource相关用法。C# 使用 CancellationTokenSource 终止线程使用CancellationTokenSo…...
整合SpringCache
整合SpringCache 1、引入依赖cache还有redis <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-cache</artifactId> </dependency>2、写配置 spring:cache:type: redis3、测试使用缓存 Cache…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
