【CSP2019 模拟赛】Time
题目描述:
小 A 现在有一个长度为 𝑛 的序列 {𝑥𝑖},但是小 A 认为这个序列不够优美。 小 A 认为一个序列是优美的,当且仅当存在 𝑘 ∈ [1, 𝑛],满足: 𝑥1 ≤ 𝑥2 ≤ … ≤ 𝑥𝑘 ≥ 𝑥𝑘+1 ≥ … ≥ 𝑥𝑛 。现在小 A 可以进行若干次操作,每次可以交换序列中相邻的两个项,现在他想知道最少操作多少次之后能够使序列变为优美的。
Input Format
第一行一个正整数 𝑛,表示序列的长度。 接下来一行 𝑛 个整数,表示初始的序列。
Output Format
输出一行一个整数,表示最少需要的操作次数。
Sample Input
5 3 4 1 2
Sample Output
1
Constraints
对于 30% 的数据,𝑛 ≤ 12。
对于 60% 的数据,𝑛 ≤ 100000, 𝑎𝑖 互不相同。
对于 100% 的数据,𝑛, 𝑎𝑖 ≤ 100000。
思路:
仔细分析题意,因只能交换序列中相邻的两个项,且要求中间数大,两端较小。可以用贪心思想将每一个小的x[i]往左或往右两端移动,取最小的交换次数,最后累加即为所求。其实就是计算每个数左边或右边比它大的数(逆序对)有多少个,取最优。
用树状数组刚好能满足快速计算逆序对的需求。注意:因数据有可能重复,我们需要将数组从大到小排序,且将数值相同的元素id大的往前放。
#include<bits/stdc++.h>
using namespace std;
int t[100005], n;
struct node {int x, id;
} a[100005], b[100005];
bool sort1(node a, node b) { //从大到小排序,值相同ID大的放前面if (a.x == b.x) return a.id > b.id;return a.x > b.x;
}
void add(int pos, int x) {while (pos <= n) {t[pos] += x;pos += -pos & pos;}
}
int sum(int pos) {int ans = 0;while (pos) {ans += t[pos];pos -= -pos & pos;}return ans;
}
int main() {int ans = 0;cin >> n;int resa[n + 1], resb[n + 1];for (int i = 1; i <= n; i++) {scanf("%d", &a[i].x);b[i].x = a[i].x; //复制一个数组用于计算右边逆序对a[i].id = i; //求i左边逆序对b[i].id = n - i + 1; //求i右边逆序对,id取反}sort(a + 1, a + 1 + n, sort1);sort(b + 1, b + 1 + n, sort1);for (int i = 1; i <= n; i++) {add(a[i].id, 1);resa[a[i].id] = sum(a[i].id - 1); //把每个i的逆序对保存到数组对应位置}memset(t, 0, sizeof(t)); //清空数组,以便计算右边逆序对for (int i = 1; i <= n; i++) {add(b[i].id, 1);resb[b[i].id] = sum(b[i].id - 1); }reverse(resb + 1, resb + 1 + n); //之前id是反向定义,需要反转数组元素for (int i = 1; i <= n; i++)ans += min(resa[i], resb[i]); //取每个i对于左右逆序对的最小值的和,即为所求cout << ans;return 0;
}
相关文章:

【CSP2019 模拟赛】Time
题目描述: 小 A 现在有一个长度为 𝑛 的序列 {𝑥𝑖},但是小 A 认为这个序列不够优美。 小 A 认为一个序列是优美的,当且仅当存在 𝑘 ∈ [1, 𝑛],满足: &#…...

二叉树相关的算法题
二叉树相关的算法题 单值二叉树 如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。 只有给定的树是单值二叉树时,才返回 true;否则返回 false。 示例 1: 输入:[1,1,1,1,1,null,1] 输出:t…...

Unity URP 曲面细分学习笔记
学百人时遇到了曲面着色器的内容,有点糊里糊涂,于是上知乎找到了两篇大佬的文章 Unity URP 曲面细分 和 Unity曲面细分笔记,本文只是自己做学习记录使用 1.曲面细分与镶嵌 曲面细分或细分曲面(Subdivision surface)是…...

每天五分钟深度学习pytorch:训练神经网络模型的基本步骤
本文重点 本文个人认为是本专栏最重要的章节内容之一,前面我们学习了pytorch中的基本数据tensor,后面我们就将学学习深度学习模型的内容了,在学习之前,我们先来看一下我们使用pytorch框架训练神经网络模型的基本步骤,然后我们下面就将这些步骤分解开来,详细学习。 代码…...

【langchain学习】使用缓存优化langchain中的LLM调用性能:内存、SQLite与Redis的对比
在处理语言模型(LLM)调用时,特别是在需要多次执行相同请求的情况下,缓存机制能够显著提升系统的性能。本文通过对比内存缓存(InMemoryCache)、SQLite缓存(SQLiteCache)和Redis缓存(RedisCache),探讨了如何在Langchain中使用这些缓存机制来优化LLM调用的性能。 代码…...

spring boot 集成EasyExcel
EasyExcel 是一个基于 Java 的快速、简洁的 Excel 处理工具,它能够在不用考虑性能和内存等因素的情况下,快速完成 Excel 的读写功能。 首先,需要在 Spring Boot 项目中引入 EasyExcel 依赖。在 pom.xml 文件中添加以下依赖: <d…...

获取对象中第一个存在的值
在JavaScript中,要从一个对象中获取第一个存在的(非undefined、非null、非空数组等)值,你可以使用Object.values()方法结合Array.prototype.find()方法。以下是一个示例代码,演示如何实现这一点: const ob…...

Python学习笔记----集合与字典
1. 字符串、列表和元组的元素都是按下标顺序排列,可通过下 标直接访问,这样的数据类型统称为序列。 其中,字符串和元组中的元素不能修改,而列表中的元素可以修改。 集合 1. 与元组和列表类似,Set (集合&a…...

c# 排序、强转枚举
List<Tuple<double,int>> mm中doble从小到大排序 mm本身排序 在C#中,如果你有一个List<Tuple<double, int>>类型的集合mm,并且你想要根据Tuple中的double值(即第一个元素)从小到大进行排序,同…...

“华为杯”第十六届中国研究生数学建模竞赛-C题:视觉情报信息分析
目录 摘 要: 一、问题重述 二、模型假设 三、符号说明 四、问题一分析与求解 4.1 问题一分析 4.2 模型建立 4.2.1 位置变换模型建立 4.2.4 多平面转换模型建立 4.3 模型求解 4.3.1 问题一图 1 结果 4.3.2 问题一图 2 结果 4.3.3 问题一图 3 结果 4.3.4 问题一图 4 结果 4.4 模…...

html+css+js网页设计 找法网2个页面(带js)ui还原度百分之90
htmlcssjs网页设计 找法网2个页面(带js)ui还原度百分之90 网页作品代码简单,可使用任意HTML编辑软件(如:Dreamweaver、HBuilder、Vscode 、Sublime 、Webstorm、Text 、Notepad 等任意html编辑软件进行运行及修改编辑…...

018 | backtrader回测反转策略
什么是反转策略? 反转策略(Reversal Strategy)是一种试图捕捉市场价格趋势逆转的交易策略。与趋势跟随策略不同,反转策略的核心理念是“物极必反”,即价格在经过一段时间的单边趋势后,往往会出现逆转的机会…...

《图解HTTP》全篇目录
前言 目前,国内讲解 HTTP 协议的书实在太少了。在我的印象中,讲解网络协议的书仅有两本。一本是《HTTP 权威指南》,但其厚度令人望而生畏;另一本是《TCP/IP 详解,卷 1》,内容艰涩难懂,学习难度…...
+Qt的软件开发—环境配置)
基于VS2019(Release_x64)+Qt的软件开发—环境配置
前置博客: 基于C高级编程语言的软件开发随记——环境变量-CSDN博客 (一)一种避免设置大量环境变量的VS2019环境配置方法 Ⅰ 解决方案资源管理器->VC目录->在包含目录/库目录中添加对应的include/lib文件夹($(So…...

【书生大模型实战营(暑假场)闯关材料】入门岛:第1关 Linux 基础知识
【书生大模型实战营(暑假场)闯关材料】入门岛:第1关 Linux 基础知识 1. 使用VScode进行SSH远程连接服务器2. 端口映射及实例参考文献 这一博客主要介绍使用VScode进行服务器远程连接及端口映射。 1. 使用VScode进行SSH远程连接服务器 安装V…...

240810-Gradio通过HTML组件打开本地文件+防止网页跳转到about:blank
A. 最终效果 B. 可通过鼠标点击打开文件,但会跳转到about:blank import gradio as gr import subprocessdef open_pptx():pptx_path /Users/liuguokai/Downloads/240528-工业大模型1.pptxtry:subprocess.Popen([open, pptx_path])return "PPTX file opened s…...

go在linux上安装
1.首先要确定Linux架构 uname -m如果你的系统是 armv7l(32-bit ARM),你需要下载 armv6l 版的Go语言。 如果你的系统是 aarch64(64-bit ARM),你需要下载 arm64 版的Go语言。 如果你的系统是 x86_64…...
)
算法日记day 35(动归之分割等和子集|最后一块石头的重量2)
一、分割等和子集 题目: 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分…...
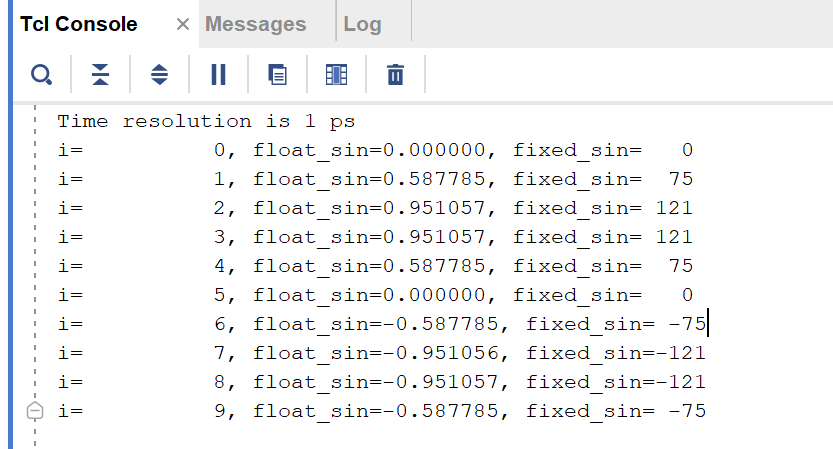
FPGA使用sv生成虚拟单音数据
FPGA使用sv生成虚拟单音数据 之前一直使用matlab生成虚拟的数据,导出到txt或是coe文件中,再导入到fpga中进行仿真测试。 复杂的数据这样操作自然是必要的,但是平日使用正弦数据进行测试的话,这样的操作不免复杂,今日…...

Linux shell编程:监控进程CPU使用率并使用 perf 抓取高CPU进程信息
0. 概要 本文将介绍一个用于监控一组进程CPU使用率的Shell脚本,,当检测到某进程的CPU使用率超出阈值时,使用 perf 工具抓取该进程的详细信息。 本shell脚本为了能在普通嵌入式系统上运行做了妥协和优化。 1. shell脚本流程的简要图示&#…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
