当前位置： 首页 > news >正文

【概念速通】李群 lie group

news 2025/12/17 17:02:59

李群 lie group 概念速通

    • 快速示例介绍：
        • 【引入】单位复数 (The unit complex numbers) 是李群 (lie group) 最简单的例子之一
        • 【进一步】SO(2): The 2D rotation matrices
        • 【Typical uses】SE(2): Pose of a robot in the plane
    • Group & Lie Group 定义：
        • 什么是 Group ?
        • 什么是 Lie Group ? 【Continuous Transformation Groups】
    • Tangent space & 两种表示方式 (Lie Algebra 和 Cartesian 笛卡尔坐标系)

在这里插入图片描述

李群的概念能够使我们构造强大的规划、控制算法

  • 强烈建议大家对照大佬的视频讲解一起看 👉 【机器人学——李群、李代数快速入门】

快速示例介绍：

【引入】单位复数 (The unit complex numbers) 是李群 (lie group) 最简单的例子之一
  • 如下图所示的 z：
【进一步】SO(2): The 2D rotation matrices

  • operator vs. vectors: 将产生旋转的主体和被旋转的元素分开，则得到下图 (李群为左图)

    • 左图：the elements that are able to transform other elements of another set (R is able to rotate x)
    • operator vs. vectors 不一定能绘制在一个图上，例如对于 S3 (The unit quaternions) 有下图
【Typical uses】SE(2): Pose of a robot in the plane
  • 将平面上的运动抽象为在球体上移动的点的运动
  • 进一步，更复杂的，例如机器人多关节在3维空间中的移动

Group & Lie Group 定义：

什么是 Group ?
  • Group Actions
什么是 Lie Group ? 【Continuous Transformation Groups】
  • Def: a group that is also a smooth manifold

Tangent space & 两种表示方式 (Lie Algebra 和 Cartesian 笛卡尔坐标系)

  • 后者 Cartesian 笛卡尔坐标系 更方便操作，更容易理解

【本篇为李群基本概念，后续会继续展开 …】

相关文章：

【概念速通】李群 lie group

李群 lie group 概念速通 快速示例介绍：【引入】单位复数 (The unit complex numbers) 是李群 (lie group) 最简单的例子之一【进一步】SO(2): The 2D rotation matrices【Typical uses】SE(2): Pose of a robot in the plane Group & Lie Group 定义&#xff1…...

编程日记 2024/8/11 17:22:48

day_39

198. 打家劫舍 class Solution:def rob(self, nums: List[int]) -> int:if len(nums) 1:return nums[0]dp [0] * len(nums)dp[0], dp[1] nums[0], max(nums[0], nums[1])for i in range(2, len(nums)):dp[i] max(dp[i - 1], dp[i - 2] nums[i])return dp[len(nums) - …...

编程日记 2024/8/11 17:21:47

计算机系统层次结构

1.计算机系统的组成 计算机系统的组成硬件系统软件系统 2.计算机的硬件部分 2.1冯诺依曼机的结构特点： 图示： 1.五大部分由运算器(ALU)，控制器(CU)，存储器(主存辅存)，输入设备，输出设备五大部分组成2.指…...

编程日记 2024/8/11 17:19:45

java语言特点

Java语言是一种广泛使用的编程语言，它具有以下几个显著的特点： 面向对象：Java是一种纯面向对象的语言，它支持类的封装、继承和多态等特性。面向对象的设计使得Java程序更加模块化，易于维护和扩展。 平台无关性&#xf…...

编程日记 2024/8/11 17:18:44

单元测试注解:@ContextConfiguration

ContextConfiguration注解 ContextConfiguration注解主要用于在‌Spring框架中加载和配置Spring上下文，特别是在测试场景中。 它允许开发者指定要加载的配置文件或配置类的位置，以便在运行时或测试时能够正确地构建和初始化Spring上下文。 基本用途和工…...

编程日记 2024/8/11 17:17:42

大数据-72 Kafka 高级特性 稳定性-事务 (概念多枯燥) 定义、概览、组、协调器、流程、中止、失败

点一下关注吧！！！非常感谢！！持续更新！！！ 目前已经更新到了： Hadoop（已更完）HDFS（已更完）MapReduce（已更完&am…...

编程日记 2024/8/11 17:16:41

MySQl 中对数据表的增删改查（基础）

MySQl 中对数据表的增删改查（基础） 新增演示插入一条数据插入多条数据 查询全列查询部分列查询查询关于列名的表达式查询时用别名查询去重后的结果查询排序后的结果条件查询比较运算符和逻辑运算符 分页查询 修改删除 黑白图是在命令行里的，彩…...

编程日记 2024/8/11 17:14:39

LVS知识点整理及实践

LVS知识点整理及实践 LVSlvs集群概念lvs概念lvs集群类型lvs-nat模型数据逻辑: lvs-DR模式数据传输和过程:特点: lvs-tun模式数据传输过程:特点: lvs-fullnet模式数据传输过程 lvs调度算法lvs调度算法类型lvs静态调度算法lvs动态调度算法4.15版本内核以后新增调度算法 ipvsadm命…...

编程日记 2024/8/11 17:13:38

Ubuntu gnome WhiteSur-gtk-theme类mac主题正确安装和卸载方式

目录 摘要目的安装和卸载特别说明 Ubuntu gnome WhiteSur-gtk-theme类mac主题正确安装和卸载方式 摘要 Ubuntu版本：ubuntu24.04 主题下载地址：https://github.com/vinceliuice/WhiteSur-gtk-theme 参考的安装教程：https://blog.51cto.com/u_…...

编程日记 2024/8/11 17:12:37

计算机毕业设计选题推荐-办公用品管理系统-Java/Python项目实战

✨作者主页：IT毕设梦工厂✨ 个人简介：曾从事计算机专业培训教学，擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

编程日记 2024/8/11 17:11:36

计算机毕业设计选题推荐-网上考试系统-Java/Python项目实战

✨作者主页：IT毕设梦工厂✨ 个人简介：曾从事计算机专业培训教学，擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

编程日记 2024/8/11 17:09:34

白骑士的Matlab教学基础篇 1.4 函数与脚本

系列目录 上一篇：白骑士的Matlab教学基础篇 1.3 控制流 函数和脚本是 MATLAB 编程中的基本组成部分，它们使得代码更加模块化、可重用和组织化。通过理解函数的定义与调用、参数与返回值，以及 MATLAB 脚本与批处理，可以显著提高编…...

编程日记 2024/8/11 17:08:33

Qt——多线程

一、QThread类 如果要设计多线程程序，一般是从QThread继承定义一个线程类，并重新定义QThread的虚函数 run() ，在函数 run() 里处理线程的事件循环。 应用程序的线程称为主线程，创建的其他线程称为工作线程。主线程的 start() 函数…...

编程日记 2024/8/11 17:05:30

技术周总结 08.05-08.11周日(scala git回滚)

文章目录 一、08.06 周二1.1) 问题01 mac安装 scala:1. 使用 Homebrew2. 使用 SDKMAN!其他注意事项1. 确认 Scala 安装位置2. 设置 PATH 环境变量对于 zsh (macOS Catalina 及更高版本默认使用 zsh):对于 bash (如果您使用的是 bash shell): 3. 验证安装 二、08.09 周五2.1&…...

编程日记 2024/8/11 17:01:25

ffmpeg 命令图片和视频转换

1、截图 ffmpeg -i d:\input.mp4 -ss 0:0:10 d:\output.jpg //指定输出分辨率 ffmpeg -i d:\input.mp4 -y -f image2 -ss 0:0:10 -vframes 1 -s 640x360 d:\output.jpg 2、视频分拆图片 ffmpeg -r 输入帧率 -i d:\input.mp4 -r 输出帧率 "d:\outputDir\frame_%04d.jp…...

编程日记 2024/8/11 16:59:22

力扣 | 动态规划 | 在字符串的应用 | 最长回文子串、最长回文子序列、单词拆分、编辑距离

文章目录 1.最长回文子串2.最长回文子序列3.单词拆分4.编辑距离5. 共同点和思路6. 各个问题的思路和扩展1. 最长回文子串2. 最长回文子序列3. 单词拆分4. 编辑距离 在解答字符串动态规划的应用时，我们需要非常注意一个问题：   有时候我们定义 d p [ i …...

编程日记 2024/8/11 16:57:20

【docker】docker容器部署常用服务

1、容器部署nginx，并且新增一个页面 docker run -d -p 81:80 --name nginx2 nginx docker exec -it nginx2 /bin/bashcd /usr/share/nginx/html/ echo "hello world">>hello.html2、容器部署redis，成功部署后向redis中添加一条数据 do…...

编程日记 2024/8/11 16:54:16

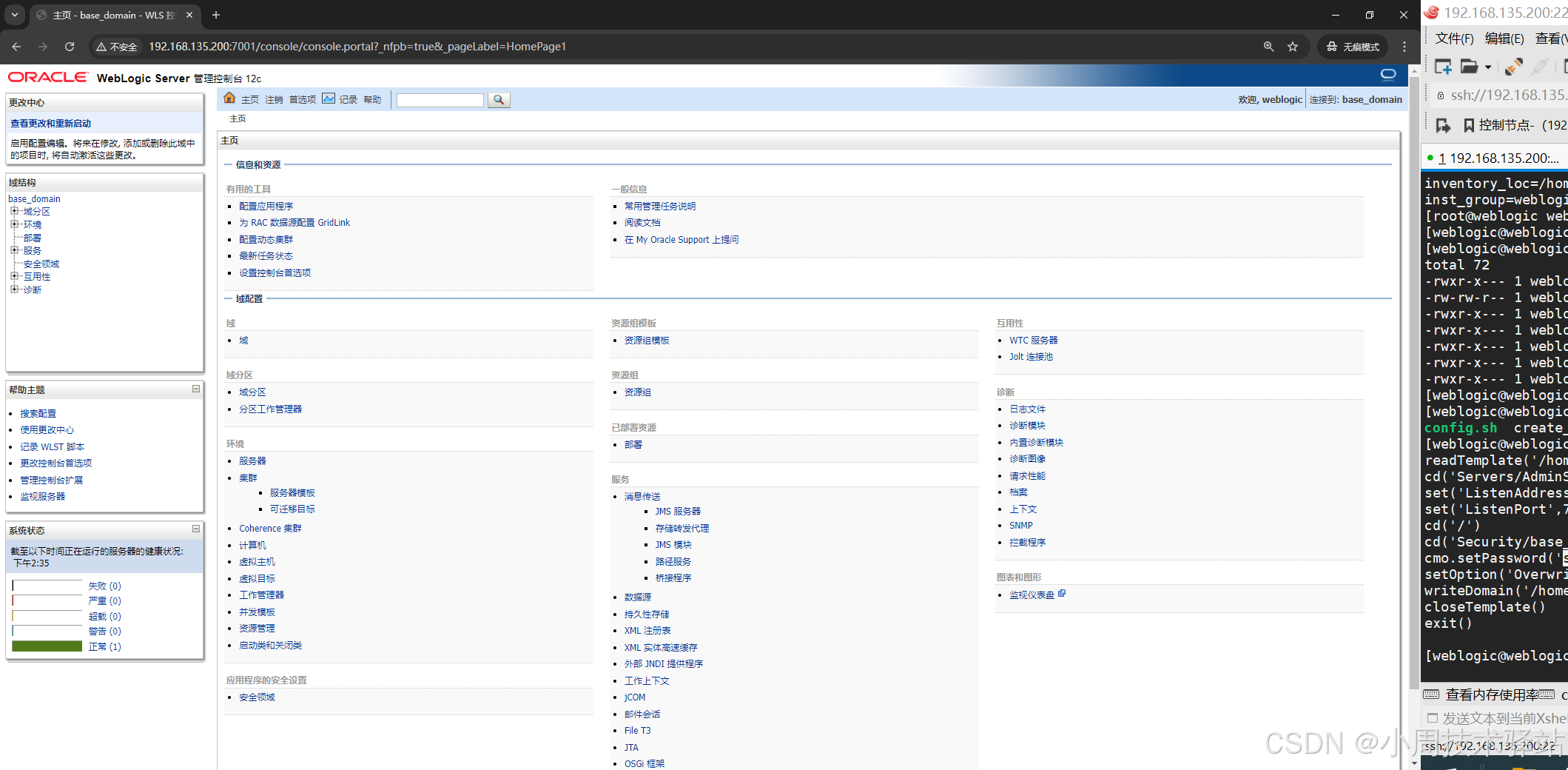
CentOS 7.6 安装 Weblogic

注：本教程是以虚拟机作为安装环境，如果您公司需要安装 Weblogic 服务器，请先以虚拟机模拟安装一遍，否则出现失误，概不负责😁。 一、环境 虚拟机：VMware Workstation 16 Linux：Cent…...

编程日记 2024/8/11 16:53:16

一键清除电脑隐私痕迹，Privacy Eraser助你轻松搞定！

前言 在数字时代，隐私就像是我们手中的细沙，不经意间就可能从指缝间溜走；你是否也曾担心，自己的每一次点击、每一次浏览，都可能成为别人眼中的“秘密”？别急，今天小江湖就要带你走进一款神秘的…...

编程日记 2024/8/11 16:50:13

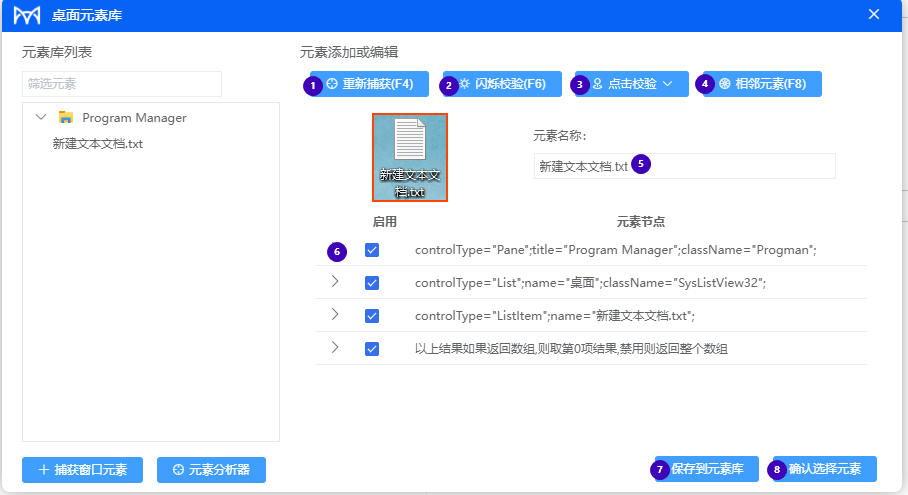
火语言RPA桌面元素库使用方法

使用火语言RPA自动选取工具获得桌面中元素： 工具标识 桌面 分组下组件若有此标识，则包含选择元素工具，点击此标识会进行选择元素操作。 桌面元素库介绍 ① 根据元素名称筛选元素库中保存的元素 ② 元素库，显示已经保存的元素名…...

编程日记 2024/8/11 16:49:12

国防科技大学计算机基础课程笔记02信息编码

1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制，因此这个了16进制的数据既可以翻译成为这个机器码，也可以翻译成为这个国标码，所以这个时候很容易会出现这个歧义的情况； 因此，我们的这个国…...

编程新知 2025/12/15 19:29:20

C++实现分布式网络通信框架RPC(3)--rpc调用端

目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中，我们已经大致实现了rpc服务端的各项功能代…...

编程新知 2025/12/13 15:51:25

python打卡day49

知识点回顾： 通道注意力模块复习空间注意力模块CBAM的定义 作业：尝试对今天的模型检查参数数目，并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

编程新知 2025/12/9 21:16:21

多场景 OkHttpClient 管理器 - Android 网络通信解决方案

下面是一个完整的 Android 实现&#xff0c;展示如何创建和管理多个 OkHttpClient 实例&#xff0c;分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

编程新知 2025/12/15 1:34:37

CentOS下的分布式内存计算Spark环境部署

一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架&#xff0c;相比 MapReduce 具有以下核心优势&#xff1a; 内存计算&#xff1a;数据可常驻内存&#xff0c;迭代计算性能提升 10-100 倍&#xff08;文档段落&#xff1a;3-79…...

编程新知 2025/12/13 22:37:00

多模态商品数据接口：融合图像、语音与文字的下一代商品详情体验

一、多模态商品数据接口的技术架构 &#xff08;一&#xff09;多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如&#xff0c;当用户上传一张“蓝色连衣裙”的图片时&#xff0c;接口可自动提取图像中的颜色&#xff08;RGB值&…...

编程新知 2025/7/23 3:55:49

MVC 数据库

MVC 数据库 引言 在软件开发领域，Model-View-Controller（MVC）是一种流行的软件架构模式，它将应用程序分为三个核心组件：模型（Model）、视图（View）和控制器（Controller）。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系，以…...

编程新知 2025/10/30 4:58:11

【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验

系列回顾&#xff1a; 在上一篇中&#xff0c;我们成功地为应用集成了数据库&#xff0c;并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了&#xff01;但是&#xff0c;如果你仔细审视那些 API&#xff0c;会发现它们还很“粗糙”&#xff1a;有…...

编程新知 2025/11/25 4:57:19

微信小程序云开发平台MySQL的连接方式

注&#xff1a;微信小程序云开发平台指的是腾讯云开发 先给结论&#xff1a;微信小程序云开发平台的MySQL&#xff0c;无法通过获取数据库连接信息的方式进行连接&#xff0c;连接只能通过云开发的SDK连接&#xff0c;具体要参考官方文档&#xff1a; 为什么&#xff1f; 因为…...

编程新知 2025/12/11 19:08:52

零基础在实践中学习网络安全-皮卡丘靶场（第九期-Unsafe Fileupload模块）（yakit方式）

本期内容并不是很难&#xff0c;相信大家会学的很愉快&#xff0c;当然对于有后端基础的朋友来说&#xff0c;本期内容更加容易了解&#xff0c;当然没有基础的也别担心&#xff0c;本期内容会详细解释有关内容 本期用到的软件&#xff1a;yakit&#xff08;因为经过之前好多期…...

编程新知 2025/12/9 14:35:12