力扣 | 动态规划 | 在字符串的应用 | 最长回文子串、最长回文子序列、单词拆分、编辑距离
文章目录
- 1.最长回文子串
- 2.最长回文子序列
- 3.单词拆分
- 4.编辑距离
- 5. 共同点和思路
- 6. 各个问题的思路和扩展
- 1. 最长回文子串
- 2. 最长回文子序列
- 3. 单词拆分
- 4. 编辑距离
在解答字符串动态规划的应用时,我们需要非常注意一个问题:
有时候我们定义 d p [ i ] [ j ] dp[i][j] dp[i][j]表示第一个字符串的第i个字符,第二个字符串的第j个字符。 d p [ 0 ] [ 0 ] dp[0][0] dp[0][0]表示两个都为空串时。
使用数组下标访问时,应该这样访问第一个字符串的第i个字符:word1[i - 1]
总的来说dp的定义可能和数组访问下标不一样。
if(word1[i - 1] == word2[j - 1])dp[i][j] = ···
我们还需要这样思考:为什么要使用动态规划?不使用其他方法?为什么动态规划可以解决?
1.最长回文子串
LeetCode:5.最长回文子串

一个回文串 s t r [ i ] [ j ] str[i][j] str[i][j]的子串有这样的性质: s t r [ i + 1 ] [ j − 1 ] str[i+1][j-1] str[i+1][j−1]也是回文串。
因此我们要判断一个子串 s t r [ i ] [ j ] str[i][j] str[i][j]是否是回文串,我们只需要知道其子串 s t r [ i + 1 ] [ j − 1 ] str[i+1][j-1] str[i+1][j−1]是否是回文串即可。我们使用 d p [ i ] [ j ] dp[i][j] dp[i][j]保存该区间[i,j]是否是回文串。
这样我们就使用回文字符串常用的解题方式——从长度为1的子串开始判断是否为回文串,判断完后长度加一,这样每次都能保证判断时,其子串都已经知道是否是回文串了。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
class Solution {
public:string longestPalindrome(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));//dp[i]表示以i结尾的 最长回文子串dp[0][0] = true;int left = 0, len = 1;for(int j = 1; j < s.size(); ++ j){int tmp = j - 1;dp[j][j] = true;if(s[tmp] == s[j]) {dp[tmp][j] =true;left = tmp; len = 2;}}for(int i = 2; i < s.size(); ++ i){//距离for(int j = i; j < s.size(); ++ j){int tmp = j - i;if(s[j] == s[tmp] ){if(dp[tmp + 1][j - 1] == true) {dp[tmp][j] = true;left = tmp; len = i + 1;}}}}return s.substr(left, len);}
};
2.最长回文子序列
LeetCode:2.最长回文子序列

与最长回文子串类似,本题的区别是,不要求子串严格是回文串,只需要包含回文串即可。
因此我们要判断一个子串 s t r [ i ] [ j ] str[i][j] str[i][j]是否包含回文串,我们只需要知道其子串 s t r [ i + 1 ] [ j − 1 ] str[i+1][j-1] str[i+1][j−1]是否包含回文串即可。我们使用 d p [ i ] [ j ] dp[i][j] dp[i][j]保存该区间[i,j]是包含的最长回文串长度。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
class Solution {
public:int longestPalindromeSubseq(string s) {int n = s.length();if(n == 1) return 1;vector<vector<int>> dp(n, vector<int>(n));for(int i = 0; i < n; ++ i) {dp[i][i] = 1;}for(int i = 1; i < n; ++ i){for(int j = i; j < n; ++ j){int l = j - i;char c1 = s[l], c2 = s[j];if(c1 == c2){dp[l][j] = dp[l + 1][j - 1] + 2;}else{dp[l][j] = max(dp[l][j - 1], dp[l + 1][j]);}}}return dp[0][n - 1];}
};
3.单词拆分
LeetCode:139. 单词拆分

这个拼接的顺序不是随便的,比如 c a t s a n d catsand catsand,字典为 [ " c a t " , " c a t s " , " a n d " ] ["cat","cats","and"] ["cat","cats","and"],如果先用 " c a t " "cat" "cat"去拼接,会导致问题无解,但实际上有解。
定义 d p [ i ] dp[i] dp[i]表示,前 i i i个字符是否可以被拼接,那么它能被拼接的话,我们用字典里面的词一个一个放到末尾,然后看 d p [ i − d i c t . s i z e ( ) ] dp[i - dict.size()] dp[i−dict.size()]能否被拼接就能知道 d p [ i ] dp[i] dp[i]能否被拼接了。
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {vector<bool> dp(s.size() + 1, false);dp[0] = true;for(int i = 1; i <= s.size(); ++ i)for(auto & str : wordDict)if(str.size() <= i && dp[i - str.size()] == true)if(s.substr(i - str.size(), str.size()) == str){dp[i] = true;break;}return dp[s.size()];}
};
4.编辑距离
LeetCode:72.编辑距离

其实动态规划问题就是思考出状态以及状态转移,比如这里你想要知道 w o r d 1 word1 word1到 w o r d 2 word2 word2转换次数,你就只需要知道其子串。
if(word1[i - 1] == word2[j - 1]){dp[i][j] = dp[i - 1][j - 1];
}else{dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
}
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));for(int i = 1; i <= word1.size(); ++ i){dp[i][0] = i;}for(int i = 1; i <= word2.size(); ++ i){dp[0][i] = i;}for(int i = 1; i <= word1.size(); ++ i){for(int j = 1; j <= word2.size(); ++ j){if(word1[i - 1] == word2[j - 1]){dp[i][j] = dp[i - 1][j - 1];}else{dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;}}}return dp[word1.size()][word2.size()];}
};
5. 共同点和思路
这些字符串相关的动态规划问题有一些共同的特点:
-
定义状态:
- 使用二维数组
dp表示两个子串之间的某种状态(如是否回文、最长子序列长度、是否可以拼接、编辑距离等)。
- 使用二维数组
-
状态转移:
- 根据问题的具体要求,定义状态转移方程,用子问题的解构建原问题的解。
-
初始化:
- 根据问题的初始条件,初始化
dp数组的边界值。
- 根据问题的初始条件,初始化
-
遍历顺序:
- 通常使用双重循环遍历所有可能的子串或子序列。
6. 各个问题的思路和扩展
1. 最长回文子串
思路:
- 定义
dp[i][j]表示字符串s从第i到第j的子串是否为回文串。 - 如果
s[i] == s[j],并且dp[i+1][j-1]为真,则dp[i][j]为真。 - 初始化单个字符的子串和长度为2的子串。
扩展:
- 可以使用中心扩展法来优化时间复杂度,从每个字符和字符间隙向两边扩展检查回文。
2. 最长回文子序列
思路:
- 定义
dp[i][j]表示字符串s从第i到第j的子串中最长回文子序列的长度。 - 如果
s[i] == s[j],则dp[i][j] = dp[i+1][j-1] + 2。 - 否则,
dp[i][j] = max(dp[i+1][j], dp[i][j-1])。
扩展:
- 可以尝试空间优化,将二维数组优化为一维数组。
3. 单词拆分
思路:
- 定义
dp[i]表示字符串s的前i个字符能否被拆分成字典中的单词。 - 对于每个位置
i,检查从j到i的子串是否在字典中,并且dp[j]是否为真。
扩展:
- 可以使用记忆化搜索或递归的方法来优化复杂度。
4. 编辑距离
思路:
- 定义
dp[i][j]表示将word1的前i个字符转换为word2的前j个字符所需的最少操作数。 - 如果
word1[i-1] == word2[j-1],则dp[i][j] = dp[i-1][j-1]。 - 否则,
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1。
扩展:
- 可以尝试空间优化,将二维数组优化为一维数组。
- 可以扩展到其他字符串变换问题,如最长公共子序列。
相关文章:

力扣 | 动态规划 | 在字符串的应用 | 最长回文子串、最长回文子序列、单词拆分、编辑距离
文章目录 1.最长回文子串2.最长回文子序列3.单词拆分4.编辑距离5. 共同点和思路6. 各个问题的思路和扩展1. 最长回文子串2. 最长回文子序列3. 单词拆分4. 编辑距离 在解答字符串动态规划的应用时,我们需要非常注意一个问题: 有时候我们定义 d p [ i …...

【docker】docker容器部署常用服务
1、容器部署nginx,并且新增一个页面 docker run -d -p 81:80 --name nginx2 nginx docker exec -it nginx2 /bin/bashcd /usr/share/nginx/html/ echo "hello world">>hello.html2、容器部署redis,成功部署后向redis中添加一条数据 do…...
CentOS 7.6 安装 Weblogic
注:本教程是以虚拟机作为安装环境,如果您公司需要安装 Weblogic 服务器,请先以虚拟机模拟安装一遍,否则出现失误,概不负责😁。 一、环境 虚拟机:VMware Workstation 16 Linux:Cent…...

一键清除电脑隐私痕迹,Privacy Eraser助你轻松搞定!
前言 在数字时代,隐私就像是我们手中的细沙,不经意间就可能从指缝间溜走;你是否也曾担心,自己的每一次点击、每一次浏览,都可能成为别人眼中的“秘密”?别急,今天小江湖就要带你走进一款神秘的…...
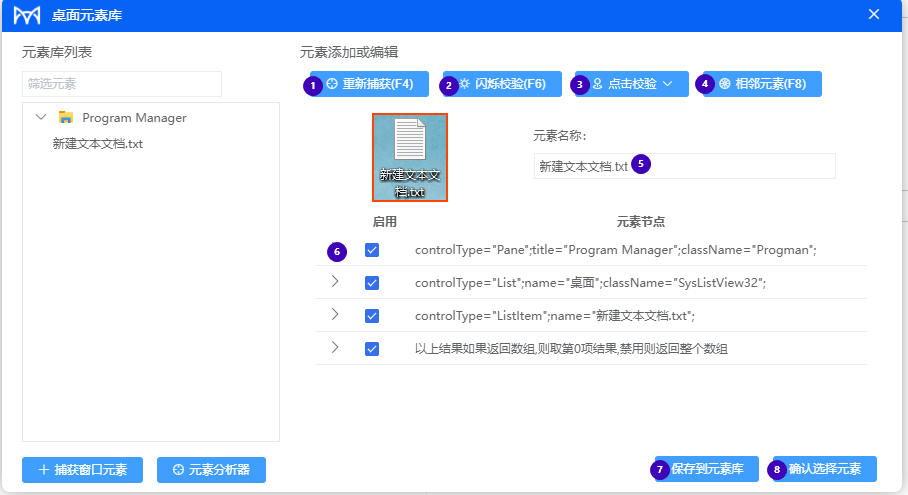
火语言RPA桌面元素库使用方法
使用火语言RPA自动选取工具获得桌面中元素: 工具标识 桌面 分组下组件若有此标识,则包含选择元素工具,点击此标识会进行选择元素操作。 桌面元素库介绍 ① 根据元素名称筛选元素库中保存的元素 ② 元素库,显示已经保存的元素名…...

FTP.JBoss,Ldap,Rsync未授权访问漏洞(附带修复方法)
一.FTP未授权访问漏洞(匿名登陆) FTP 弱⼝令或匿名登录漏洞,⼀般指使⽤ FTP 的⽤户启⽤了匿名登录功能,或系统⼝令的⻓度太短、复杂度不够、仅包含数字、或仅包含字⺟等,容易被⿊客攻击,发⽣恶意⽂件上传或更严重的⼊侵⾏为。 漏…...

全新在线客服系统源码(pc+h5+uniapp+公众号小程序+抖音)附搭建接入教程
全新在线客服系统源码介绍 一、系统概述与优势 本系统是一款基于PHP的开源在线客服系统,支持PC端、移动端(小程序)、H5页面以及Uniapp多端接入。系统利用网络技术和人工智能技术,实现用户与客服人员的即时聊天沟通,有…...

为具有公网IPV6地址的服务器安装nextcloudAIO并使用NginxProxyManager配置反向代理
软件和硬件环境 ubuntu server 24.04,并已配置好ipv6公网地址,已安装好docker和docker-compose。一块单独的硬盘,用于单独存储nextcloud数据。(非必需)有一个能够正常解析的域名,并已配置好AAAA记录解析。…...

挖矿宝藏之TCP/IP
目录 一、TCP/IP简介 1.TCP自述 2.IP自述 二、TCP/IP 寻址 1.IP V6 2.域名 三、TCP/IP协议 一、TCP/IP简介 TCP/IP 指传输控制协议/网际协议(Transmission Control Protocol / Internet Protocol),是供已连接因特网的计算机进行通信的…...
略谈set与map的pair封装与进入哈希
引子:之前我们讲了红黑树的自实现,与小小的接口实现,那set与map的pair封装是如何实现的呢?,今天我们来一探究竟,而且我们也要进入新章节--哈希 对于operator--()的封装: 注意:牢记思…...

android13 串口编号修改 串口名修改
总纲 android13 rom 开发总纲说明 目录 1.前言 2.技术分析 别名定义的语法规则 3.修改示例 使用别名 注意事项 4.不生效分析 5.编译查看 6.其他方法 7.彩蛋 1.前言 更改Android设备的串口编号涉及对系统深层次的配置进行修改,通常是为了解决硬件兼容性问题或满足特…...
工作中常用的软件竟可直接下载0.5m卫星影像(Esri影像、天地图、星图)、DEM、土地覆盖数据...
之前我们有介绍过在ArcGIS通过插件、WTMS或者lyr添加谷歌影像、天地图等各种在线图源。今天我们就来再整理一套既方便查看又方便下载的教程,软件就是我们常用的Global Mapper,有点强。 这里我们整理了一些我们工作学习中常用的一些数据下载方法…...

1章3节:R 语言的产生与发展轨迹
R语言诞生于1990年代,由统计学家Ross Ihaka和Robert Gentleman在新西兰奥克兰大学开发,旨在提供一种免费开源、灵活强大的统计编程工具。R语言基于S语言的设计理念,并通过其开源社区的贡献迅速发展,形成了庞大的生态系统,包括CRAN、RStudio和Shiny等。R语言以其强大的统计…...

html常用标签
一、无序列表 ul li 注意事项:ul下面不可以嵌套其他标签,li下可以 二、有序列表 ol li 注意事项同无序列表 三、自定义列表 dd dt 注意事项同无序列表 四 、表格 table tr:行 th:表头 td:内容 4.1合并单元格 步骤 1.明确合并的目标 2.保留…...
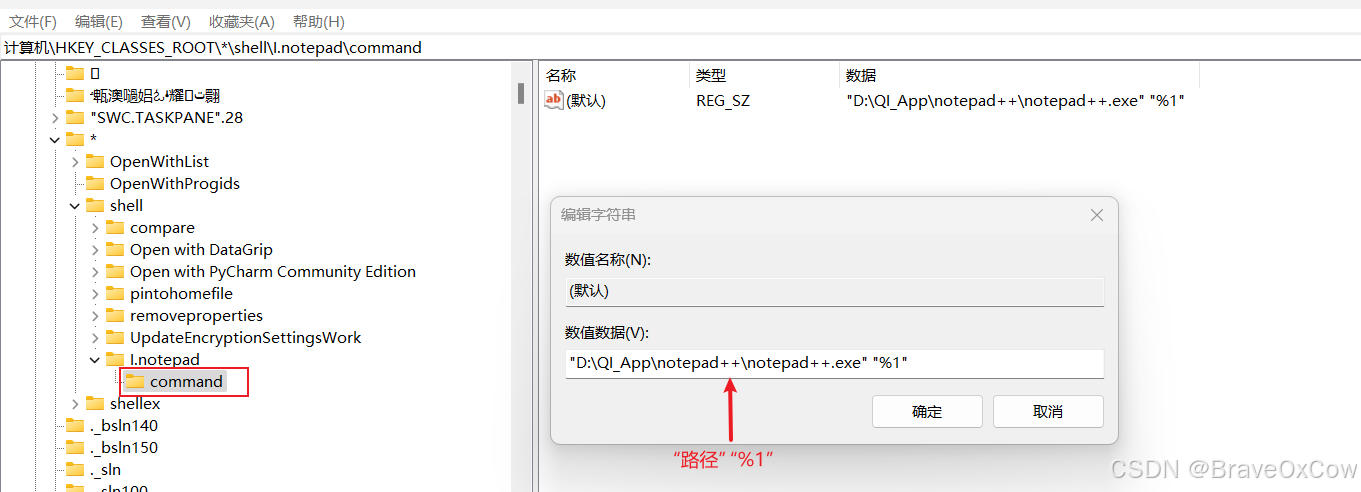
选择文件鼠标右键自定义菜单
注册表路径 计算机\HKEY_CLASSES_ROOT\*\shell 效果 操作 1.定位 winr,输入regedit, 地址栏输入以下路径,并回车。 计算机\HKEY_CLASSES_ROOT\*\shell 2.在shell上右键,新建项 3右键新建字符串值,Icon,Position 4 右键新建c…...
Linux远程访问与控制:安全与最佳实践)
Linux安全与高级应用(九)Linux远程访问与控制:安全与最佳实践
文章目录 Linux远程访问与控制:安全与最佳实践引言一、SSH服务的基本概述二、密钥对验证的SSH体系三、TCP Wrappers的使用四、构建安全的SSH服务实践五、结论 👍 个人网站:【 洛秋导航】【洛秋资源小站】 Linux远程访问与控制:安全…...

前端已经学会vue,做粒子效果
目录 1. Canvas API 2. WebGL 3. 粒子系统 4. 动画与性能优化 5. 现有库和框架 6. Vue 组件和状态管理 实践项目建议 案例1 案例2雪花 已经熟悉了 Vue、TypeScript 和 JavaScript,下面是一些你可以学习的内容,以帮助你实现粒子效果的界面&#…...

Nessus——全面的漏洞扫描神器
一、引言 在网络安全的领域中,及时发现和评估系统中的漏洞是保障网络安全的关键步骤。Nessus 作为一款备受认可的漏洞扫描工具,为企业和安全专业人员提供了强大而全面的漏洞检测和评估功能。本文将深入介绍 Nessus 的特点、功能、使用方法以及其在实际应…...

自动化部署的艺术:Conda包依赖管理的终极指南
标题:自动化部署的艺术:Conda包依赖管理的终极指南 在当今快速发展的科学计算和数据分析领域,Conda已成为Python开发者和数据科学家的首选包管理器之一。它不仅能够管理Python包,还能处理不同语言环境的依赖关系,确保…...
--IBERT IP核的使用)
详解Xilinx FPGA高速串行收发器GTX/GTP(7)--IBERT IP核的使用
目录 1、什么是IBERT? 2、IBERT IP核的使用 3、Example Design的使用 4、IBERT的测试 4.1、误码率测试 4.2、眼图测试 4.3、回环测试(Loopback) 5、源码下载 文章总目录点这里:《FPGA接口与协议》专栏的说明与导航 1、什么是IBERT? IBERT就是Xilinx提…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
