略谈set与map的pair封装与进入哈希
引子:之前我们讲了红黑树的自实现,与小小的接口实现,那set与map的pair封装是如何实现的呢?,今天我们来一探究竟,而且我们也要进入新章节--哈希
对于operator--()的封装:
注意:牢记思考的方向始终是中序
示意图:


stl代码实现:
void decrement(){if (node->color == __rb_tree_red &&node->parent->parent == node)node = node->right;else if (node->left != 0) {base_ptr y = node->left;while (y->right != 0)y = y->right;node = y;}else {base_ptr y = node->parent;while (node == y->left) {node = y;y = y->parent;}node = y;}}
};自实现:我们在传的时候要传一下_root,因为我们不是通过以上stl中hearer的方式
迭代器部分更改:
Node* _root;RBTreeIterator(Node*node,Node*root):_node(node),_root(root)
{}self& operator--()
{if (_node == nullptr) {//找最右节点Node* rightMost = _root;while (rightMost && rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}else if (_node->_left){Node* rightMost = _node->_left;while (rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = cur->_parent;}_node = parent;}return *this;
}对于set的insert封装:
//插入
pair<iterator,bool>insert(const T& data)
{//空树新增节点,也是红黑树Node* root = _root;if (root == nullptr){root = new Node(data);_root = root;_root->_col = BLACK;return make_pair(iterator(_root, _root), true);}//红黑树大逻辑K_of_T kot;Node* cur = _root;Node* parent = nullptr;//要先找到,插入位置while (cur){if (kot(data) < kot(cur->_Data)){parent = cur;cur = cur->_left;}else if (kot(data) > kot(cur->_Data)){parent = cur;cur = cur->_right;}else{return make_pair(iterator(cur, _root), false);}}cur = new Node(data);// 新增节点。颜色红色给红色cur->_col = RED;Node* newNode = cur;if (kot(parent->_Data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更改颜色//现在cur为新增节点while (parent && parent->_col==RED){Node* grandfather = parent->_parent;//找出叔叔节点if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情况一if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{//情况二// g// p u//cif (parent->_left == cur){RotateR(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{//情况三// g// p u// c// //双旋RotateL(parent);RotateR(grandfather);//注意cur与parent调了一下位置cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;//情况一if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{ //情况二// g// u p// cif (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}//情况三// g// u p// c else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//确保根节点为黑的_root->_col = BLACK;return make_pair(iterator(newNode, _root), true);
}对于:map的话,只要将k对应的vaule输出就行!,注意调用的时候也要改为pair<iterator,bool>!
什么是哈希?
一,哈希是一种数学函数,它接受一个输入(或“消息”),然后返回一个通常更小的固定大小的输出,这个输出称为“哈希值”或“哈希码”。
二,哈希也是一种思想:映射:哈希思想通过哈希函数将任意长度的数据映射到固定长度的哈希值。这个映射过程是单向的,即从数据到哈希值是容易的,但从哈希值回溯到原始数据几乎是不可能的。快速性:哈希函数的设计旨在快速计算,以便在大数据集中实现高效的数据访问。均匀分布:理想情况下,哈希函数应该能够将输入数据均匀地分布在哈希值空间中,以减少冲突并提高查找效率。
哈希的应用:
哈希思想在数据库索引、密码存储、信息检索、数据同步、数字签名、区块链技术等多个领域都有广泛的应用。通过哈希,可以有效地管理和访问大量数据,同时保证数据的安全性和完整性。
由哈希来的哈希表(unordered)
一,背景:
在C++98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到log_2N,即最差情况下需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好 的查询是,进行很少的比较次数就能够将元素找到,因此在C++11中,STL又提供了4个 unordered系列的关联式容器,这四个容器与红黑树结构的关联式容器使用方式基本类似,只是其底层结构不同,
以下是unordered_set与set的区别图,我们可以更加看到底层结构为哈希表的优势!

对于调试性能,大家可以通过以下代码进行测试:
#include<unordered_set>
#include<iostream>
#include<set>using namespace std;int test_set2()
{const size_t N = 10000000;unordered_set<int> us;set<int> s;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; ++i){//v.push_back(rand()); // N比较大时,重复值比较多//v.push_back(rand()+i); // 重复值相对少v.push_back(i); // 没有重复,有序}size_t begin1 = clock();for (auto e : v){s.insert(e);}size_t end1 = clock();cout << "set insert:" << end1 - begin1 << endl;size_t begin2 = clock();for (auto e : v){us.insert(e);}size_t end2 = clock();cout << "unordered_set insert:" << end2 - begin2 << endl;int m1 = 0;size_t begin3 = clock();for (auto e : v){auto ret = s.find(e);if (ret != s.end()){++m1;}}size_t end3 = clock();cout << "set find:" << end3 - begin3 << "->" << m1 << endl;int m2 = 0;size_t begin4 = clock();for (auto e : v){auto ret = us.find(e);if (ret != us.end()){++m2;}}size_t end4 = clock();cout << "unorered_set find:" << end4 - begin4 << "->" << m2 << endl;cout << "插入数据个数:" << s.size() << endl;cout << "插入数据个数:" << us.size() << endl << endl;size_t begin5 = clock();for (auto e : v){s.erase(e);}size_t end5 = clock();cout << "set erase:" << end5 - begin5 << endl;size_t begin6 = clock();for (auto e : v){us.erase(e);}size_t end6 = clock();cout << "unordered_set erase:" << end6 - begin6 << endl << endl;return 0;
}int main()
{test_set2();return 0;
}可以有以下的结果:只展示一种

哈希函数
引起哈希冲突的一个原因可能是:哈希函数设计不够合理。
哈希函数设计原则:
哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值 域必须在0到m-1之间
哈希函数计算出来的地址能均匀分布在整个空间中
哈希函数应该比较简单
常见的哈希函数包括以下几种类型:(最常用的,用颜色标出了)
直接定址法:使用关键字本身作为哈希地址,例如年龄作为关键字时,年龄值直接作为哈希地址
数字分析法:选择数字的某些部分作为哈希地址,避免使用重复可能性大的数字前几位
平方取中法:取关键字平方后的中间几位作为哈希地址
折叠法:将关键字分割成位数相同的几部分,然后取这几部分的叠加和作为哈希地址
除留余数法:使用关键字除以一个不大于哈希表大小的数后的余数作为哈希地址,公式为 H(key) = key%p (p ≤ m) ;
随机数法:使用随机函数作为哈希地址,适用于关键字长度不等的情况
加法哈希:通过将字符串中每个字符的ASCII值累加得到哈希值
位运算Hash:利用位运算(如移位和异或)混合输入元素,例如旋转Hash
乘法Hash:使用乘法的不相关性,例如使用乘数31的String类的hashCode()方法
除法Hash:虽然不常用,但除法也具有不相关性,可以用于哈希函数
查表Hash:如CRC系列算法,通过查找预设的表来实现快速哈希
混合哈希算法:结合以上各种方式,例如MD5、Tiger等,它们通常用于需要高安全性的场合
哈希冲突解决
哈希冲突
哈希冲突,也称为哈希碰撞,是指两个不同的输入值通过哈希函数计算后得到相同的哈希值。由于哈希函数的输出长度是固定的,而输入数据可以是无限的,理论上讲,任何哈希函数都可能发生冲突.
解决哈希冲突两种常见的方法是:闭散列和开散列
一,什么是闭散列

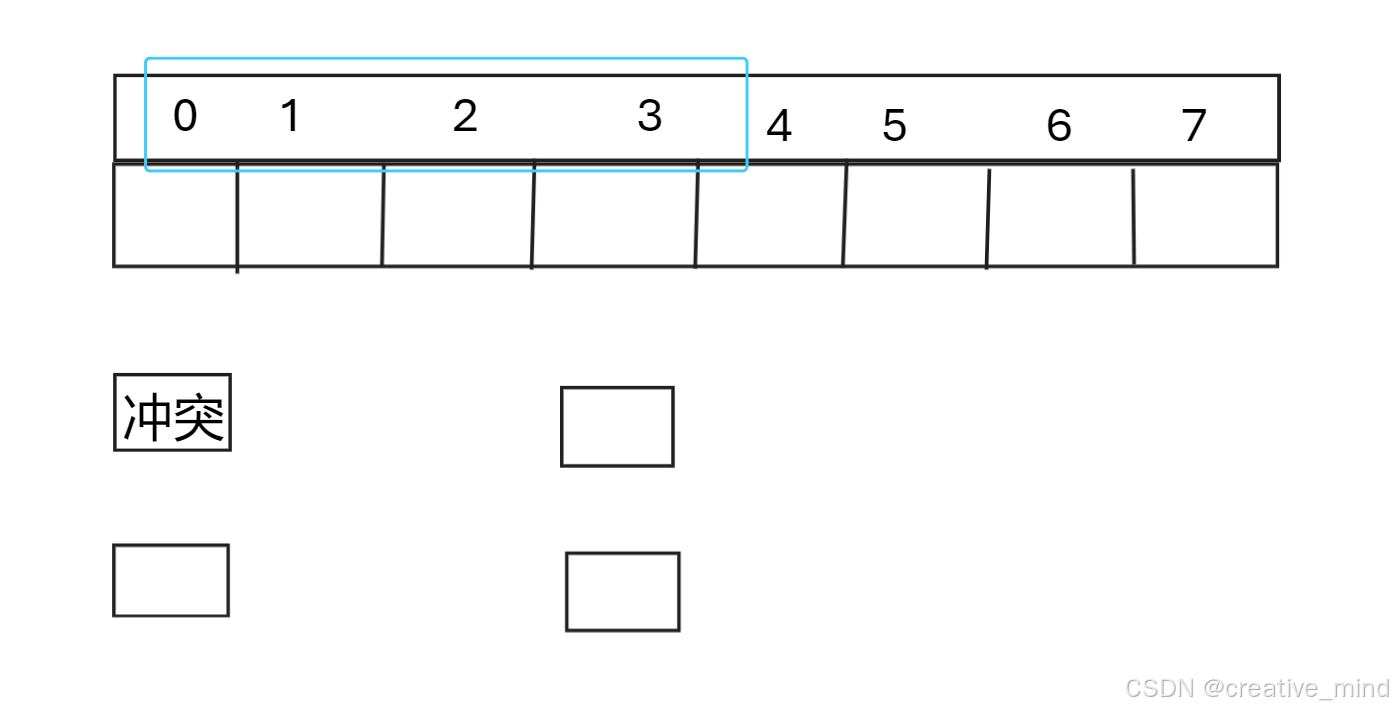
也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有 空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置 呢?
1.1,线性探测(需要枚举3种状态)
-
计算哈希值:首先,使用哈希函数计算键(key)的哈希值,确定它在哈希表中的理论位置。
-
检查冲突:如果该位置已被占用(即发生冲突),则按照固定间隔(通常是1)移动到下一个位置。
-
探测序列:继续线性地探测下一个位置,直到找到一个空闲位置。
-
插入元素:一旦找到空闲位置,将元素插入到该位置。
-
处理表满:如果探测到表的末尾仍未找到空闲位置,则循环回到表的开头继续探测。
-
查找元素:在查找元素时,也需要从哈希值对应的位置开始,按照相同的探测序列查找,直到找到目标元素或遇到一个空闲位置(表示元素不存在)。
-
删除元素:删除元素时,不能简单地将位置置为空,因为这会打断查找其他元素的探测序列。通常使用一个特殊的标记(如“已删除”标记)来代替真正的空位。
1.2,二次探测(需要枚举3种状态)
-
计算哈希值:首先,使用哈希函数计算键的哈希值,确定它在哈希表中的理论位置。
-
发生冲突:如果该位置已被占用,计算下一个探测位置,公式为: 探测位置=(原始位置)+i^2 其中 i 是探测的第几次尝试(i=1,2,3,…)
-
探测序列:探测位置是原始哈希值加上 i^2 的结果,这样探测的间隔会随着 i 的增加而增加(1, 4, 9, 16, ...)。
-
插入元素:当找到一个空闲位置时,将元素插入到该位置。
-
循环探测:如果探测到表尾,继续从表头开始探测,直到找到空闲位置。
-
查找元素:查找时,也需要按照相同的探测序列进行查找,直到找到目标元素或确定元素不存在。
-
删除元素:与线性探测类似,不能简单地将位置置为空,而是使用一个特殊的标记来表示该位置已被删除。
其他:平衡因子:
哈希的平衡因子,也称为荷载因子(Load Factor),是衡量哈希表性能的一个重要参数。它定义为哈希表中已存储元素的数量与哈希表的总槽位数(即哈希表的大小)之比。荷载因子用以下公式表示
荷载因子=已存储元素的数量/哈希表的大小
荷载因子反映了哈希表的填充程度,对哈希表的性能有直接影响
二,什么是开散列,就是说
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地 址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链 接起来,各链表的头结点存储在哈希表中。
下节,我将详细讲解哈希表,已经自实现!,希望帮到大家!
相关文章:

略谈set与map的pair封装与进入哈希
引子:之前我们讲了红黑树的自实现,与小小的接口实现,那set与map的pair封装是如何实现的呢?,今天我们来一探究竟,而且我们也要进入新章节--哈希 对于operator--()的封装: 注意:牢记思…...

android13 串口编号修改 串口名修改
总纲 android13 rom 开发总纲说明 目录 1.前言 2.技术分析 别名定义的语法规则 3.修改示例 使用别名 注意事项 4.不生效分析 5.编译查看 6.其他方法 7.彩蛋 1.前言 更改Android设备的串口编号涉及对系统深层次的配置进行修改,通常是为了解决硬件兼容性问题或满足特…...
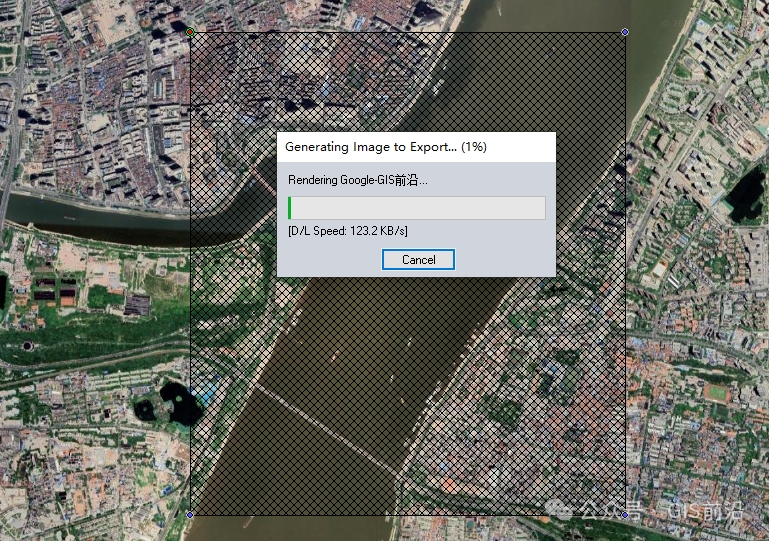
工作中常用的软件竟可直接下载0.5m卫星影像(Esri影像、天地图、星图)、DEM、土地覆盖数据...
之前我们有介绍过在ArcGIS通过插件、WTMS或者lyr添加谷歌影像、天地图等各种在线图源。今天我们就来再整理一套既方便查看又方便下载的教程,软件就是我们常用的Global Mapper,有点强。 这里我们整理了一些我们工作学习中常用的一些数据下载方法…...

1章3节:R 语言的产生与发展轨迹
R语言诞生于1990年代,由统计学家Ross Ihaka和Robert Gentleman在新西兰奥克兰大学开发,旨在提供一种免费开源、灵活强大的统计编程工具。R语言基于S语言的设计理念,并通过其开源社区的贡献迅速发展,形成了庞大的生态系统,包括CRAN、RStudio和Shiny等。R语言以其强大的统计…...

html常用标签
一、无序列表 ul li 注意事项:ul下面不可以嵌套其他标签,li下可以 二、有序列表 ol li 注意事项同无序列表 三、自定义列表 dd dt 注意事项同无序列表 四 、表格 table tr:行 th:表头 td:内容 4.1合并单元格 步骤 1.明确合并的目标 2.保留…...
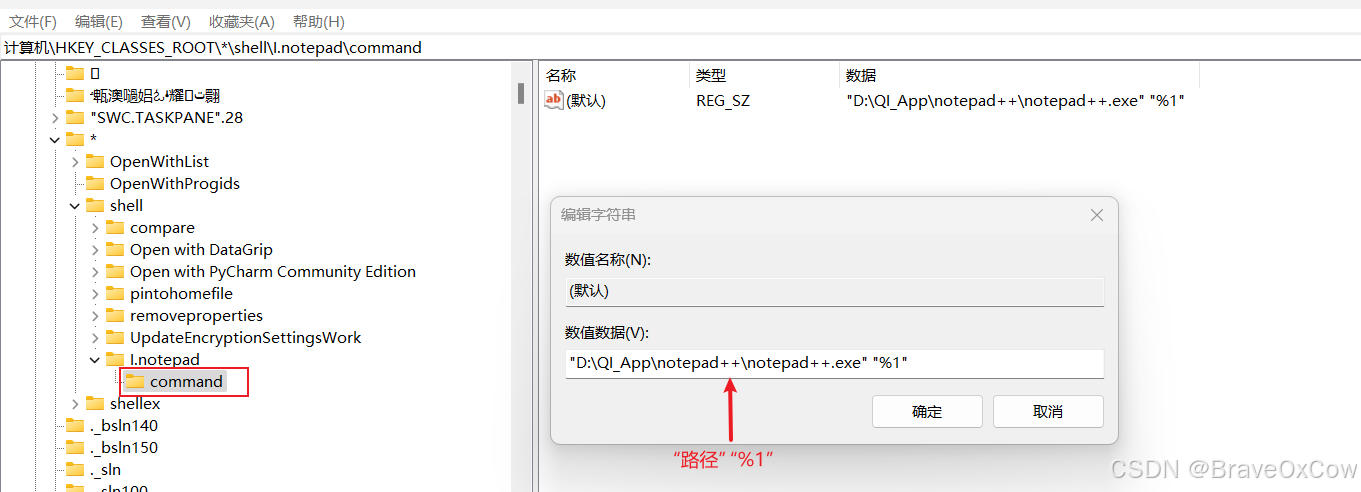
选择文件鼠标右键自定义菜单
注册表路径 计算机\HKEY_CLASSES_ROOT\*\shell 效果 操作 1.定位 winr,输入regedit, 地址栏输入以下路径,并回车。 计算机\HKEY_CLASSES_ROOT\*\shell 2.在shell上右键,新建项 3右键新建字符串值,Icon,Position 4 右键新建c…...
Linux远程访问与控制:安全与最佳实践)
Linux安全与高级应用(九)Linux远程访问与控制:安全与最佳实践
文章目录 Linux远程访问与控制:安全与最佳实践引言一、SSH服务的基本概述二、密钥对验证的SSH体系三、TCP Wrappers的使用四、构建安全的SSH服务实践五、结论 👍 个人网站:【 洛秋导航】【洛秋资源小站】 Linux远程访问与控制:安全…...

前端已经学会vue,做粒子效果
目录 1. Canvas API 2. WebGL 3. 粒子系统 4. 动画与性能优化 5. 现有库和框架 6. Vue 组件和状态管理 实践项目建议 案例1 案例2雪花 已经熟悉了 Vue、TypeScript 和 JavaScript,下面是一些你可以学习的内容,以帮助你实现粒子效果的界面&#…...

Nessus——全面的漏洞扫描神器
一、引言 在网络安全的领域中,及时发现和评估系统中的漏洞是保障网络安全的关键步骤。Nessus 作为一款备受认可的漏洞扫描工具,为企业和安全专业人员提供了强大而全面的漏洞检测和评估功能。本文将深入介绍 Nessus 的特点、功能、使用方法以及其在实际应…...

自动化部署的艺术:Conda包依赖管理的终极指南
标题:自动化部署的艺术:Conda包依赖管理的终极指南 在当今快速发展的科学计算和数据分析领域,Conda已成为Python开发者和数据科学家的首选包管理器之一。它不仅能够管理Python包,还能处理不同语言环境的依赖关系,确保…...
--IBERT IP核的使用)
详解Xilinx FPGA高速串行收发器GTX/GTP(7)--IBERT IP核的使用
目录 1、什么是IBERT? 2、IBERT IP核的使用 3、Example Design的使用 4、IBERT的测试 4.1、误码率测试 4.2、眼图测试 4.3、回环测试(Loopback) 5、源码下载 文章总目录点这里:《FPGA接口与协议》专栏的说明与导航 1、什么是IBERT? IBERT就是Xilinx提…...
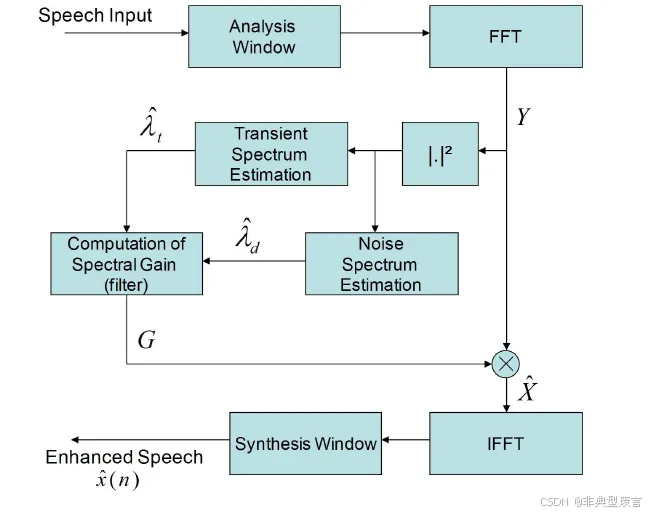
瞬态噪声抑制算法流程解析
在语音增强领域,噪声通常可以分为稳态噪声(例如白噪声)和瞬态噪声(也称为非稳态噪声,如键盘声)。对于熟悉语音降噪的读者来说,通常的信号处理方法对稳态噪声有较好的效果,具体可以参考WebRTC ANR流程解析。然而,对于瞬态噪声,由于噪声变化迅速,传统的噪声估计算法难…...

只用一个 HTML 元素可以写出多少形状?——多边形篇
上一篇章的末尾,我们只用一个 div 元素写了一个鸡蛋,在欧几里得平面几何中,鸡蛋的形状已经不能算是标准形状了。对于非标准的形状,没有比较直观的几何规律,命名方面也更加困难,俗称不规则图形,在…...
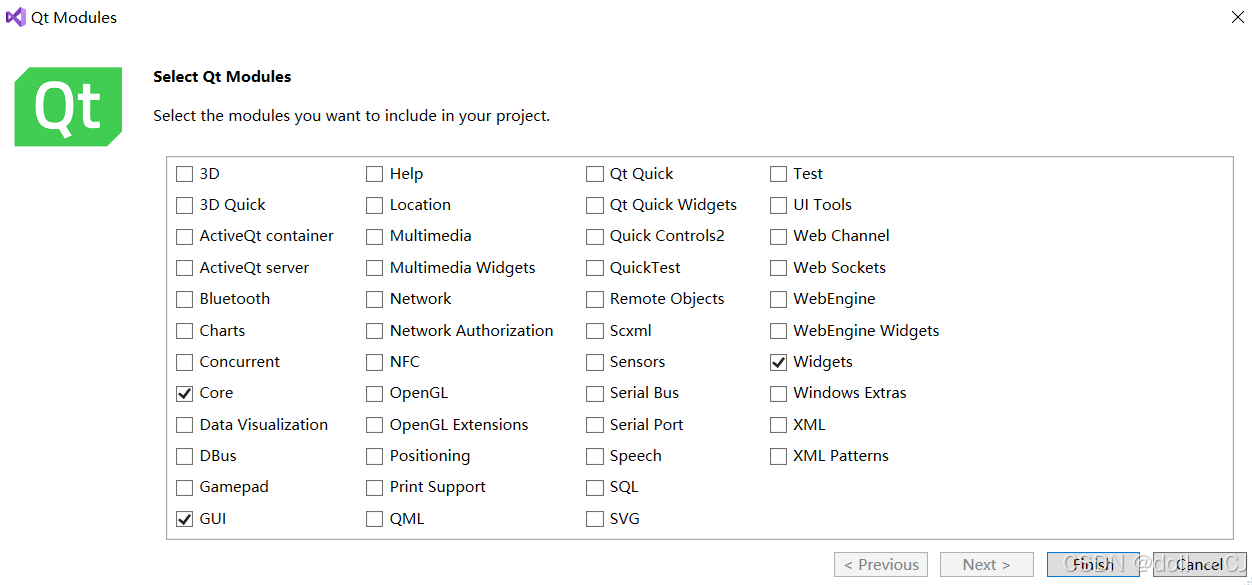
QT界面设计开发(Visual Studio 2019)—学习记录一
一、控件升级 简要介绍: 简单来说,控件提升就是将一个基础控件(Base Widget)转换为一个更特定、更复杂的自定义控件(Custom Widget)。这样做的目的是为了在设计界面时能够使用更多高级功能,而不…...

Kafka 单机和集群环境部署教程
目录 一、Kafka 单机环境部署1. 环境准备2. 安装 Java3. 安装 ZooKeeper3.1 下载并解压 ZooKeeper3.2 配置 ZooKeeper3.3 启动 ZooKeeper3.4 验证 ZooKeeper 是否正常运行 4. 安装 Kafka4.1 下载并解压 Kafka4.2 配置 Kafka4.3 创建日志目录4.4 启动 Kafka Broker4.5 验证 Kafk…...
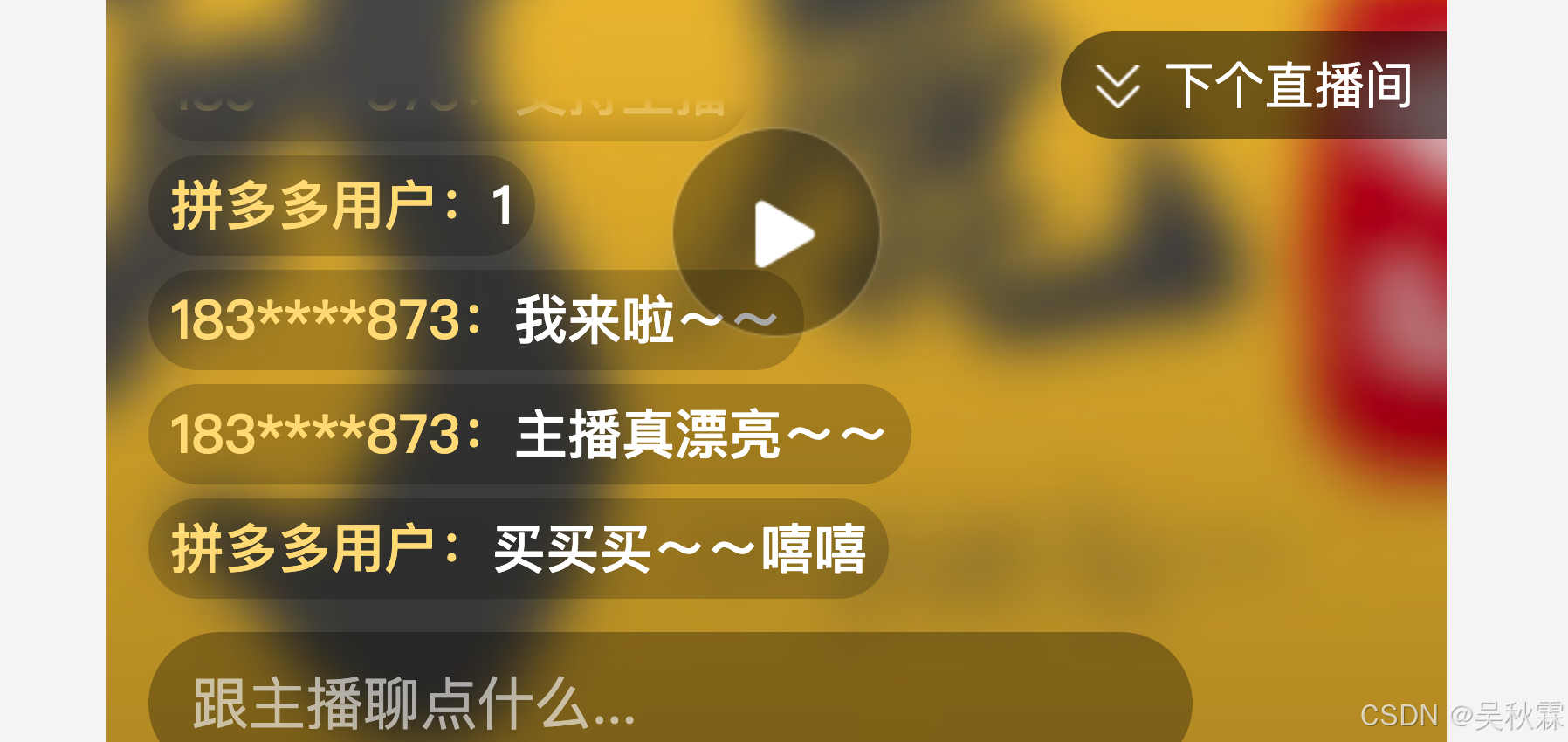
使用Python发送PDD直播间弹幕(协议算法分析)
文章目录 1. 写在前面2. 接口分析3. 算法还原 【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python…...
-PAT甲级真题)
1056. Mice and Rice (25)-PAT甲级真题
当时没想到可以用队列来做,就傻傻的模拟了,用cur存当前轮的id,这个id对应的是order的下标,这里有个求rank的技巧就是当前轮没有晋级的rank为(当前轮的组数1) 模拟: #include<bits/stdc.h&g…...

色轮在数据可视化中的应用
在数据可视化中,色彩的运用不仅仅是为了美观,更是为了传达信息、区分数据和提升图表的易读性。本文探讨色轮及其色彩公式的应用,帮助大家更好地运用色彩来提升数据可视化的效果。 1、色轮的基础概念 色轮是一个用于表示颜色之间关系的图形工…...

编程-设计模式 8:组合模式
设计模式 8:组合模式 定义与目的 定义:组合模式又称为部分-整体模式,它允许你将对象组合成树形结构来表示“部分-整体”的层次结构。组合模式使得用户对单个对象和组合对象的使用具有一致性。目的:该模式的主要目的是将多个对象…...

c语言指针(8.11)
那这样p和*p记录的地址不一样了吗? 不,p 和 *p 记录的地址在某种意义上是“相同”的,但它们在类型和使用方式上有所不同。 p 的地址:p 是一个指针,它本身存储了一个地址,这个地址是二维数组 arr 的第一行&a…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
