QT界面设计开发（Visual Studio 2019）—学习记录一

一、控件升级

简要介绍：

        简单来说，控件提升就是将一个基础控件（Base Widget）转换为一个更特定、更复杂的自定义控件（Custom Widget）。这样做的目的是为了在设计界面时能够使用更多高级功能，而不仅仅是Qt库提供的基础控件。在C++编程的经典名著《Effective C++》中，Scott Meyers强调了“接口和实现分离”的重要性。控件提升正是这一原则的一个应用：你可以在不改变界面设计的情况下，更换控件的底层实现[2] 。

一般引入操作：

        解决方案资源管理器->右键项目名称->Add（添加）->New Item（新建项）->Qt->Qt Class->设置Base class和Constructor signature->创建后编写相关升级功能；

        进入UI界面->右键待升级对象->Promote to->设置对应创建的升级控件对象（Base class name / Promoted class name）->Add->Promote。

二、Qt Modules的使用

简要介绍：

        Qt Modules包含Qt Essentials和Qt Add-Ons两部分。Qt Essentials是通用基本模块，其定义了Qt在所有平台上的基础，可在所有受支持的开发平台和经过测试的目标平台上使用；Qt Add-Ons是附加组件，其要么为了功能完整而向后兼容，要么仅适用于某些平台。每个附加组件都单独具有兼容性承诺。详细Qt Modules文档可参考/*2*/。

引入操作：

        解决方案资源管理器->右键项目名称->属性->配置属性->Qt Project Settings->General->Qt Modules->Select Modules...->选择添加需要的模块以进行快速开发。

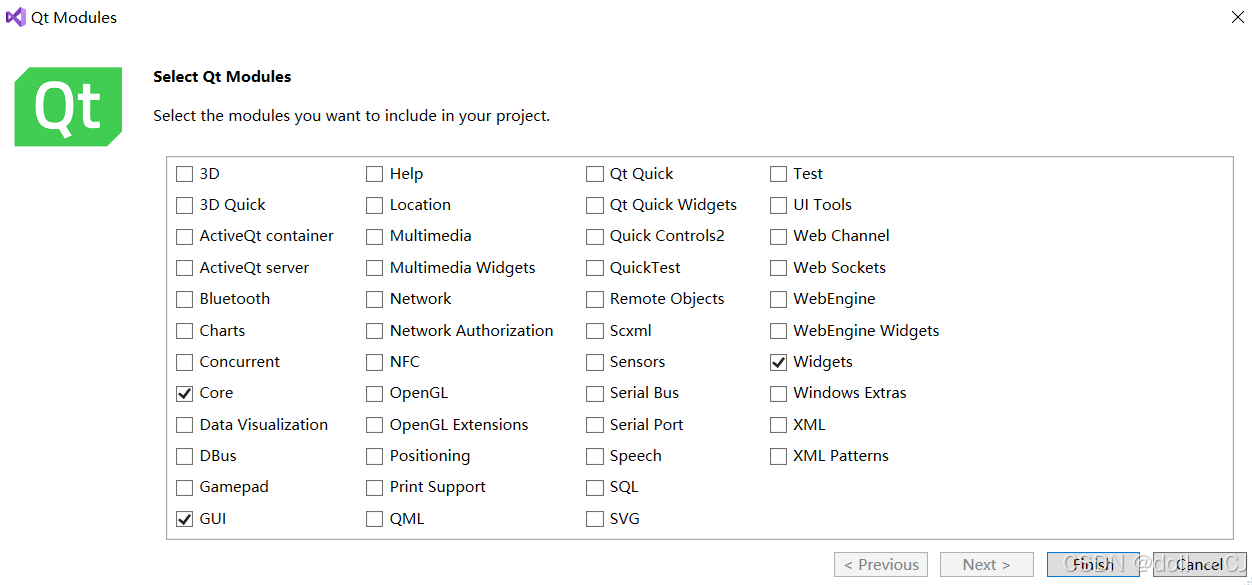
QT设计开发资源：

/*1*/ iconfont-阿里巴巴矢量图标库

/*2*/ All Modules | Qt 6.7

参考资料：

[1] Qt Assistant（QT助手/QT参考文档）

[2] 【Qt 控件】Qt 控件提升指南：从基础到高级应用_qt高级控件-CSDN博客