当前位置： 首页 > news >正文

html常用标签

news 2026/2/10 12:07:04

一、无序列表

ul li 

注意事项：ul下面不可以嵌套其他标签，li下可以

二、有序列表 

ol li 

注意事项同无序列表

三、自定义列表

dd dt

 注意事项同无序列表

四 、表格

table

tr：行

th:表头

td:内容

4.1合并单元格

步骤

1.明确合并的目标

2.保留最左上的单元格，添加属性，取值是数字，表示要合并的单元格数量

rowspan:跨行，保留最上

colspan:跨列，保留最左

3.删除其他单元格 

五、input标签

type属性

text：文本框，不可换行

password：密码框

radio：单选框

checkbox：多选框

file：上传文件 

提示信息：placeholder 

单选框需要使用name属性，例如性别：gender

默认选中：checked 

六、下拉菜单

select嵌套option

默认选中：selected 

七、文本域

textarea

可多行输入，大小由css控制，可放大缩小功能一般禁用 

八、label标签

用label标签绑定文字和表单控件的关系，增大表单控件的点击范围

例如

<label><input type="radio" name="gender">女</label> 

九、按钮

button

type属性值

submit：提交按钮，点击后提交数据到后台（默认）

reset：重置按钮，点击后将表单控件恢复到默认值

button：普通按钮，结合js使用 

十、盒子标签

div：换行时使用

span：不换行使用 

相关文章：

html常用标签

一、无序列表 ul li 注意事项&#xff1a;ul下面不可以嵌套其他标签&#xff0c;li下可以 二、有序列表 ol li 注意事项同无序列表 三、自定义列表 dd dt 注意事项同无序列表 四 、表格 table tr&#xff1a;行 th:表头 td:内容 4.1合并单元格 步骤 1.明确合并的目标 2.保留…...

编程日记 2024/8/11 16:37:59

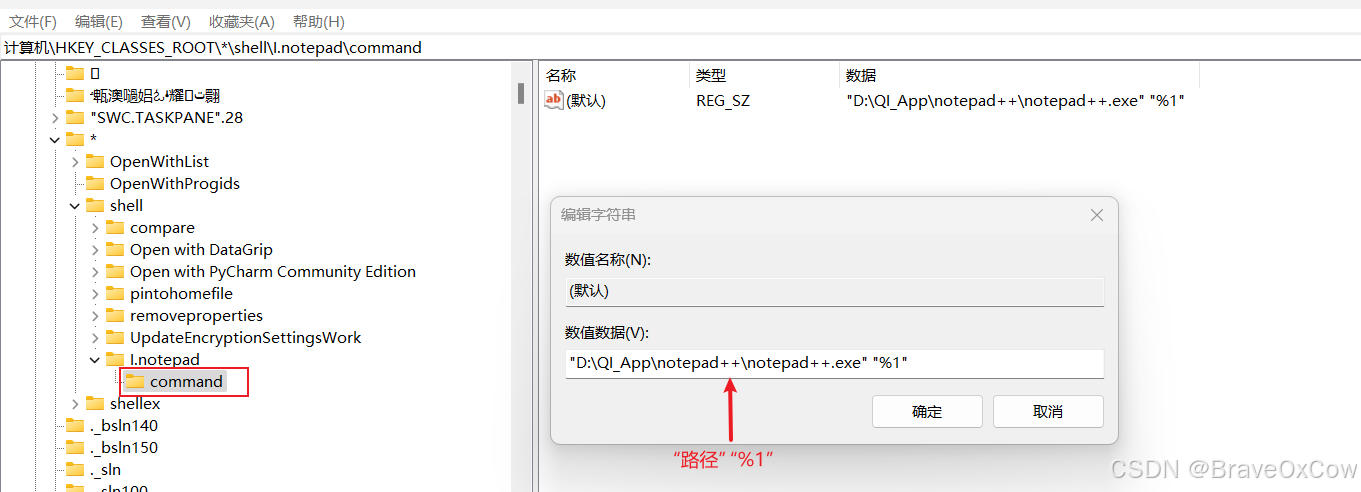
选择文件鼠标右键自定义菜单

注册表路径 计算机\HKEY_CLASSES_ROOT\*\shell 效果 操作 1.定位 winr&#xff0c;输入regedit, 地址栏输入以下路径&#xff0c;并回车。 计算机\HKEY_CLASSES_ROOT\*\shell 2.在shell上右键&#xff0c;新建项 3右键新建字符串值&#xff0c;Icon,Position 4 右键新建c…...

编程日记 2024/8/11 16:36:57

Linux安全与高级应用（九）Linux远程访问与控制：安全与最佳实践

文章目录 Linux远程访问与控制&#xff1a;安全与最佳实践引言一、SSH服务的基本概述二、密钥对验证的SSH体系三、TCP Wrappers的使用四、构建安全的SSH服务实践五、结论 &#x1f44d; 个人网站&#xff1a;【 洛秋导航】【洛秋资源小站】 Linux远程访问与控制&#xff1a;安全…...

编程日记 2024/8/11 16:35:56

前端已经学会vue，做粒子效果

目录 1. Canvas API 2. WebGL 3. 粒子系统 4. 动画与性能优化 5. 现有库和框架 6. Vue 组件和状态管理 实践项目建议 案例1 案例2雪花 已经熟悉了 Vue、TypeScript 和 JavaScript&#xff0c;下面是一些你可以学习的内容&#xff0c;以帮助你实现粒子效果的界面&#…...

编程日记 2024/8/11 16:34:55

Nessus——全面的漏洞扫描神器

一、引言 在网络安全的领域中&#xff0c;及时发现和评估系统中的漏洞是保障网络安全的关键步骤。Nessus 作为一款备受认可的漏洞扫描工具&#xff0c;为企业和安全专业人员提供了强大而全面的漏洞检测和评估功能。本文将深入介绍 Nessus 的特点、功能、使用方法以及其在实际应…...

编程日记 2024/8/11 16:33:54

自动化部署的艺术：Conda包依赖管理的终极指南

标题&#xff1a;自动化部署的艺术&#xff1a;Conda包依赖管理的终极指南 在当今快速发展的科学计算和数据分析领域&#xff0c;Conda已成为Python开发者和数据科学家的首选包管理器之一。它不仅能够管理Python包&#xff0c;还能处理不同语言环境的依赖关系&#xff0c;确保…...

编程日记 2024/8/11 16:32:52

详解Xilinx FPGA高速串行收发器GTX/GTP（7）--IBERT IP核的使用

目录 1、什么是IBERT？ 2、IBERT IP核的使用 3、Example Design的使用 4、IBERT的测试 4.1、误码率测试 4.2、眼图测试 4.3、回环测试（Loopback） 5、源码下载 文章总目录点这里：《FPGA接口与协议》专栏的说明与导航 1、什么是IBERT？ IBERT就是Xilinx提…...

编程日记 2024/8/11 16:31:51

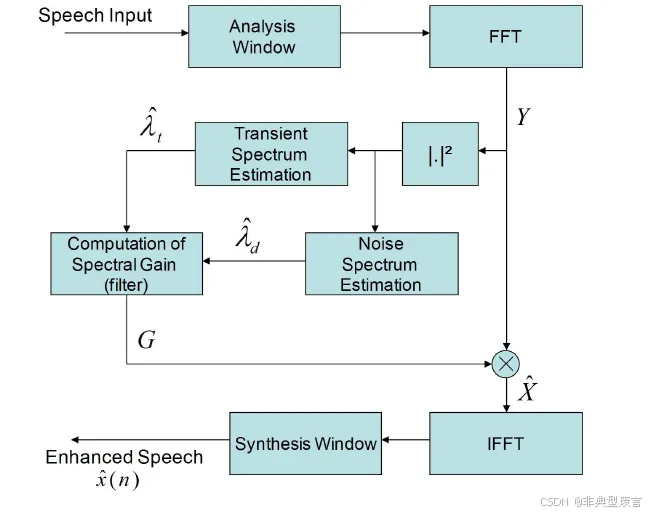
瞬态噪声抑制算法流程解析

在语音增强领域，噪声通常可以分为稳态噪声（例如白噪声）和瞬态噪声（也称为非稳态噪声，如键盘声）。对于熟悉语音降噪的读者来说，通常的信号处理方法对稳态噪声有较好的效果，具体可以参考WebRTC ANR流程解析。然而，对于瞬态噪声，由于噪声变化迅速，传统的噪声估计算法难…...

编程日记 2024/8/11 16:27:45

只用一个 HTML 元素可以写出多少形状？——多边形篇

上一篇章的末尾&#xff0c;我们只用一个 div 元素写了一个鸡蛋&#xff0c;在欧几里得平面几何中&#xff0c;鸡蛋的形状已经不能算是标准形状了。对于非标准的形状&#xff0c;没有比较直观的几何规律&#xff0c;命名方面也更加困难&#xff0c;俗称不规则图形&#xff0c;在…...

编程日记 2024/8/11 16:26:44

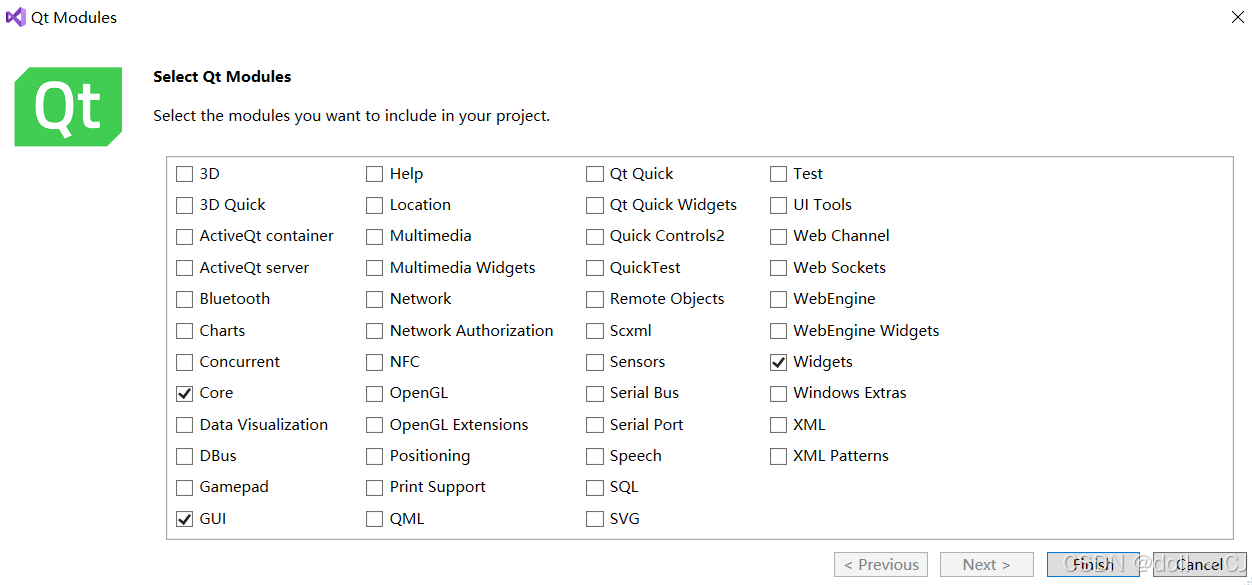
QT界面设计开发（Visual Studio 2019）—学习记录一

一、控件升级 简要介绍&#xff1a; 简单来说&#xff0c;控件提升就是将一个基础控件&#xff08;Base Widget&#xff09;转换为一个更特定、更复杂的自定义控件&#xff08;Custom Widget&#xff09;。这样做的目的是为了在设计界面时能够使用更多高级功能&#xff0c;而不…...

编程日记 2024/8/11 16:25:42

Kafka 单机和集群环境部署教程

目录 一、Kafka 单机环境部署1. 环境准备2. 安装 Java3. 安装 ZooKeeper3.1 下载并解压 ZooKeeper3.2 配置 ZooKeeper3.3 启动 ZooKeeper3.4 验证 ZooKeeper 是否正常运行 4. 安装 Kafka4.1 下载并解压 Kafka4.2 配置 Kafka4.3 创建日志目录4.4 启动 Kafka Broker4.5 验证 Kafk…...

编程日记 2024/8/11 16:21:36

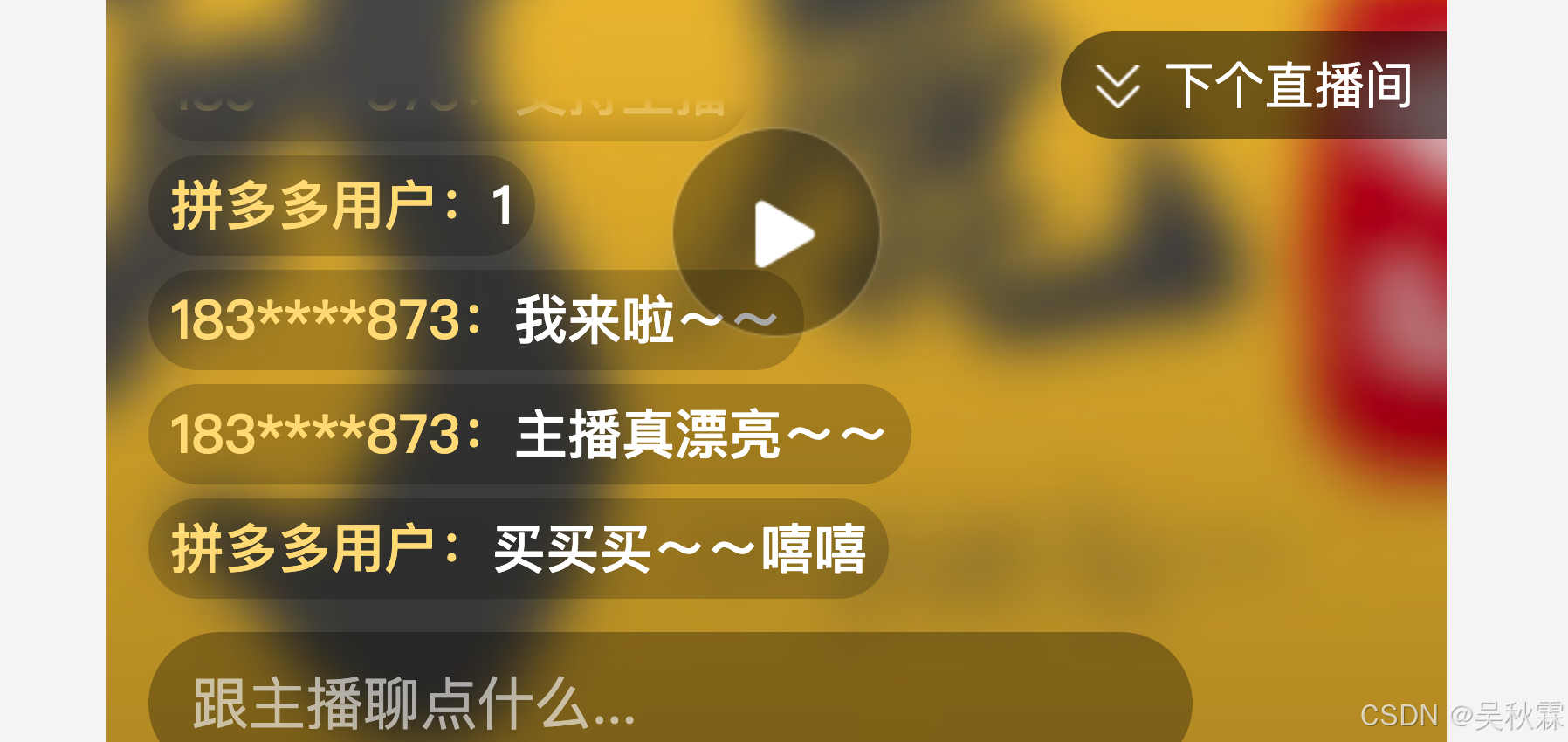
使用Python发送PDD直播间弹幕（协议算法分析）

文章目录 1. 写在前面2. 接口分析3. 算法还原 【&#x1f3e0;作者主页】&#xff1a;吴秋霖 【&#x1f4bc;作者介绍】&#xff1a;擅长爬虫与JS加密逆向分析&#xff01;Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python…...

编程日记 2024/8/11 16:20:35

1056. Mice and Rice (25)-PAT甲级真题

当时没想到可以用队列来做&#xff0c;就傻傻的模拟了&#xff0c;用cur存当前轮的id&#xff0c;这个id对应的是order的下标&#xff0c;这里有个求rank的技巧就是当前轮没有晋级的rank为&#xff08;当前轮的组数1&#xff09; 模拟&#xff1a; #include<bits/stdc.h&g…...

编程日记 2024/8/11 16:17:33

色轮在数据可视化中的应用

在数据可视化中&#xff0c;色彩的运用不仅仅是为了美观&#xff0c;更是为了传达信息、区分数据和提升图表的易读性。本文探讨色轮及其色彩公式的应用&#xff0c;帮助大家更好地运用色彩来提升数据可视化的效果。 1、色轮的基础概念 色轮是一个用于表示颜色之间关系的图形工…...

编程日记 2024/8/11 16:16:32

编程-设计模式 8：组合模式

设计模式 8&#xff1a;组合模式 定义与目的 定义&#xff1a;组合模式又称为部分-整体模式&#xff0c;它允许你将对象组合成树形结构来表示“部分-整体”的层次结构。组合模式使得用户对单个对象和组合对象的使用具有一致性。目的&#xff1a;该模式的主要目的是将多个对象…...

编程日记 2024/8/11 16:15:31

c语言指针（8.11）

那这样p和*p记录的地址不一样了吗&#xff1f; 不&#xff0c;p 和 *p 记录的地址在某种意义上是“相同”的&#xff0c;但它们在类型和使用方式上有所不同。 p 的地址&#xff1a;p 是一个指针&#xff0c;它本身存储了一个地址&#xff0c;这个地址是二维数组 arr 的第一行&a…...

编程日记 2024/8/11 16:14:30

加密技术的发展

加密是一种用于保护数据安全的技术&#xff0c;通过将原始信息&#xff08;明文&#xff09;转换为一种不可读的形式&#xff08;密文&#xff09;&#xff0c;确保只有拥有正确解密密钥的人才能访问其真实内容。加密技术在现代社会中被广泛应用于各种场景&#xff0c;包括但不…...

编程日记 2024/8/11 16:12:28

编程-设计模式 22：策略模式

设计模式 22&#xff1a;策略模式 定义与目的 定义&#xff1a;策略模式定义了一系列算法&#xff0c;并将每一个算法封装起来&#xff0c;使它们可以互相替换。策略模式让算法的变化独立于使用算法的客户。目的&#xff1a;该模式的主要目的是将一组相关的算法封装成一系列可…...

编程日记 2024/8/11 16:11:27

kafka 将log4j的项目升级到log4j2

kafka版本是kafka_2.11-2.0.0&#xff0c;由于引用的log4j有漏洞&#xff0c;而升级kafka可能影响比较大&#xff0c;所以更新log4j包的版本。 参考的是将log4j的项目升级到log4j2 主要步骤如下&#xff1a; cd kafka的目录 cd libs rm -f slf4j-log4j12-1.7.25.jar rm -f …...

编程日记 2024/8/11 16:10:25

【CSP2019 模拟赛】Time

题目描述&#xff1a; 小 A 现在有一个长度为 &#x1d45b; 的序列 {&#x1d465;&#x1d456;}&#xff0c;但是小 A 认为这个序列不够优美。 小 A 认为一个序列是优美的&#xff0c;当且仅当存在 &#x1d458; ∈ [1, &#x1d45b;]&#xff0c;满足&#xff1a; &#…...

编程日记 2024/8/11 16:09:23

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析

一、变量声明设计&#xff1a;let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性&#xff0c;这种设计体现了语言的核心哲学。以下是深度解析&#xff1a; 1.1 设计理念剖析 安全优先原则&#xff1a;默认不可变强制开发者明确声明意图 let x 5; …...

编程新知 2025/9/28 20:12:12

谷歌浏览器插件

项目中有时候会用到插件 sync-cookie-extension1.0.0&#xff1a;开发环境同步测试 cookie 至 localhost&#xff0c;便于本地请求服务携带 cookie 参考地址&#xff1a;https://juejin.cn/post/7139354571712757767 里面有源码下载下来&#xff0c;加在到扩展即可使用FeHelp…...

编程新知 2025/8/16 3:55:30

华为OD机试-食堂供餐-二分法

import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

编程新知 2026/1/28 11:11:03

AI书签管理工具开发全记录（十九）：嵌入资源处理

1.前言 &#x1f4dd; 在上一篇文章中&#xff0c;我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源&#xff0c;方便后续将资源打包到一个可执行文件中。 2.embed介绍 &#x1f3af; Go 1.16 引入了革命性的 embed 包&#xff0c;彻底改变了静态资源管理的…...

编程新知 2026/1/30 16:24:23

关键领域软件测试的突围之路：如何破解安全与效率的平衡难题

在数字化浪潮席卷全球的今天&#xff0c;软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件&#xff0c;这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下&#xff0c;实现高效测试与快速迭代&#xff1f;这一命题正考验着…...

编程新知 2026/1/27 13:20:11

在Ubuntu24上采用Wine打开SourceInsight

1. 安装wine sudo apt install wine 2. 安装32位库支持，SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库（解决显示问题） sudo apt install fonts-wqy…...

编程新知 2025/10/14 0:47:25

Java + Spring Boot + Mybatis 实现批量插入

在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法&#xff1a;使用 MyBatis 的 <foreach> 标签和批处理模式&#xff08;ExecutorType.BATCH&#xff09;。 方法一&#xff1a;使用 XML 的 <foreach> 标签&#xff…...

编程新知 2025/6/11 2:44:05

R语言速释制剂QBD解决方案之三

本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

编程新知 2026/2/9 2:43:24

算法：模拟

1.替换所有的问号 1576. 替换所有的问号 - 力扣&#xff08;LeetCode&#xff09; ​遍历字符串​&#xff1a;通过外层循环逐一检查每个字符。​遇到 ? 时处理​&#xff1a; 内层循环遍历小写字母&#xff08;a 到 z&#xff09;。对每个字母检查是否满足&#xff1a; ​与…...

编程新知 2026/2/10 11:15:52

wpf在image控件上快速显示内存图像

wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像&#xff08;比如分辨率3000*3000的图像&#xff09;的办法&#xff0c;尤其是想把内存中的裸数据&#xff08;只有图像的数据&#xff0c;不包…...

编程新知 2026/1/31 9:25:11