排序算法——简单选择排序
一、算法原理
简单选择排序是一种基本的排序算法,其原理是每次从未排序的元素中选择最小(或最大)的元素,然后与未排序部分的第一个元素交换位置,直到所有元素都被排序。
二、算法实现流程
简单选择排序法(Simple Selection Sort)就是通过n-i次关键字间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i(1<i<n)个记录交换之。

三、代码示例
#include <stdio.h>
void Swap(int *a,int *b)
{int temp = *a;*a = *b;*b = temp;
}void SelectSort(int *arr,int size)
{int j,i,min;for(i = 0;i < size;i++){min = i; /*将当前下标定义为最小值下标*/for(j = i + 1;j < size;j++) /*循环之后的数据*/{if(arr[min] > arr[j]) /*如果有小于当前最小值的关键字*/{min = j; /*将此关键字的下标赋值给min*/}}if(min != i) /*若min不等于i,说明找到最小值,交换*/{Swap(&arr[i],&arr[min]); /*将最小值和arr[i]的值进行交换*/} }
}
void print(int *arr,int size)
{for (int i = 0; i < size; i++){printf("%d ", arr[i]);}printf("\n");
}int main()
{int arr[] = {5,4,3,6,2,0,1};int size = sizeof(arr)/sizeof(int);SelectSort(arr,size);printf("简单排序后的数组如下:");print(arr,size);return 0;
}运行结果:

四、简单选择算法的复杂度分析


相关文章:

排序算法——简单选择排序
一、算法原理 简单选择排序是一种基本的排序算法,其原理是每次从未排序的元素中选择最小(或最大)的元素,然后与未排序部分的第一个元素交换位置,直到所有元素都被排序。 二、算法实现流程 简单选择排序法(Simple Se…...
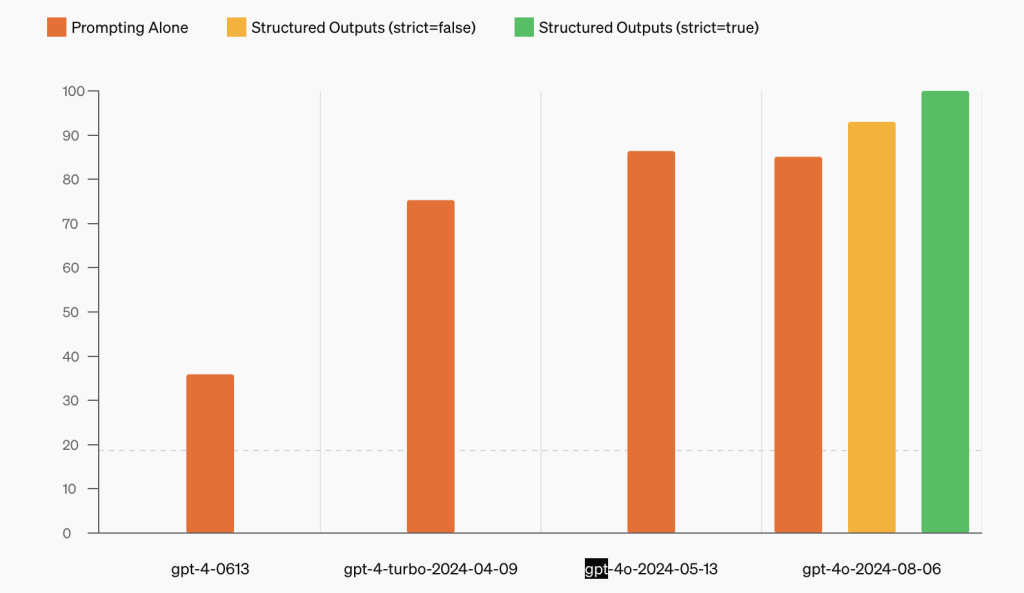
OpenAI API推出结构化输出功能
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
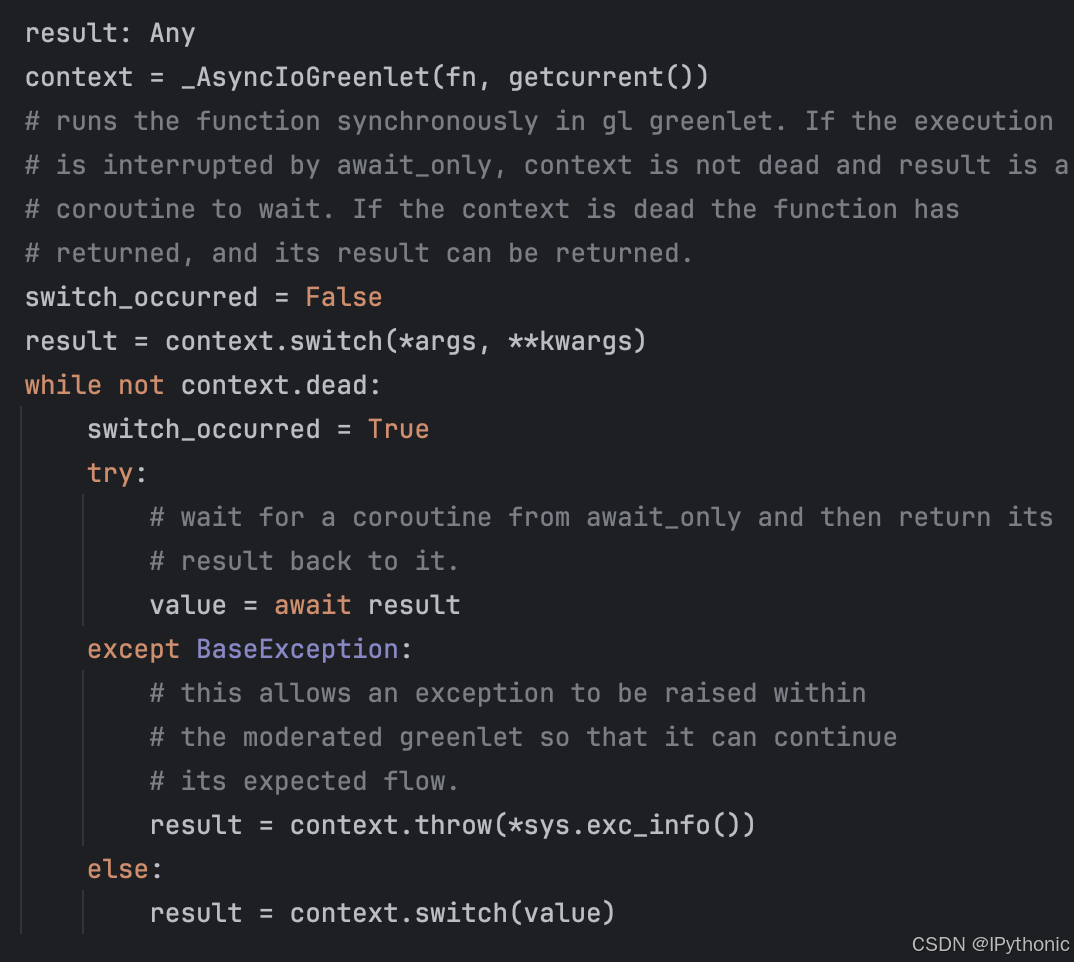
Python 异步编程:Sqlalchemy 异步实现方式
SQLAlchemy 是 Python 中最流行的数据库工具之一,在新版本中引入了对异步操作的支持。这为使用异步框架(如 FastAPI)开发应用程序带来了极大的便利。在这篇文章中,简单介绍下 SQLAlchemy 是如何利用 Greenlet 实现异步操作的。 什…...

父类引用指向子类对象
在 Java 中,父类引用可以指向子类对象,这是多态的一种表现。这种特性允许你使用父类的引用来操作子类对象,从而实现更灵活和可扩展的代码设计。 基本概念 多态:父类引用可以指向子类对象。这使得你可以用统一的接口处理不同的对象…...
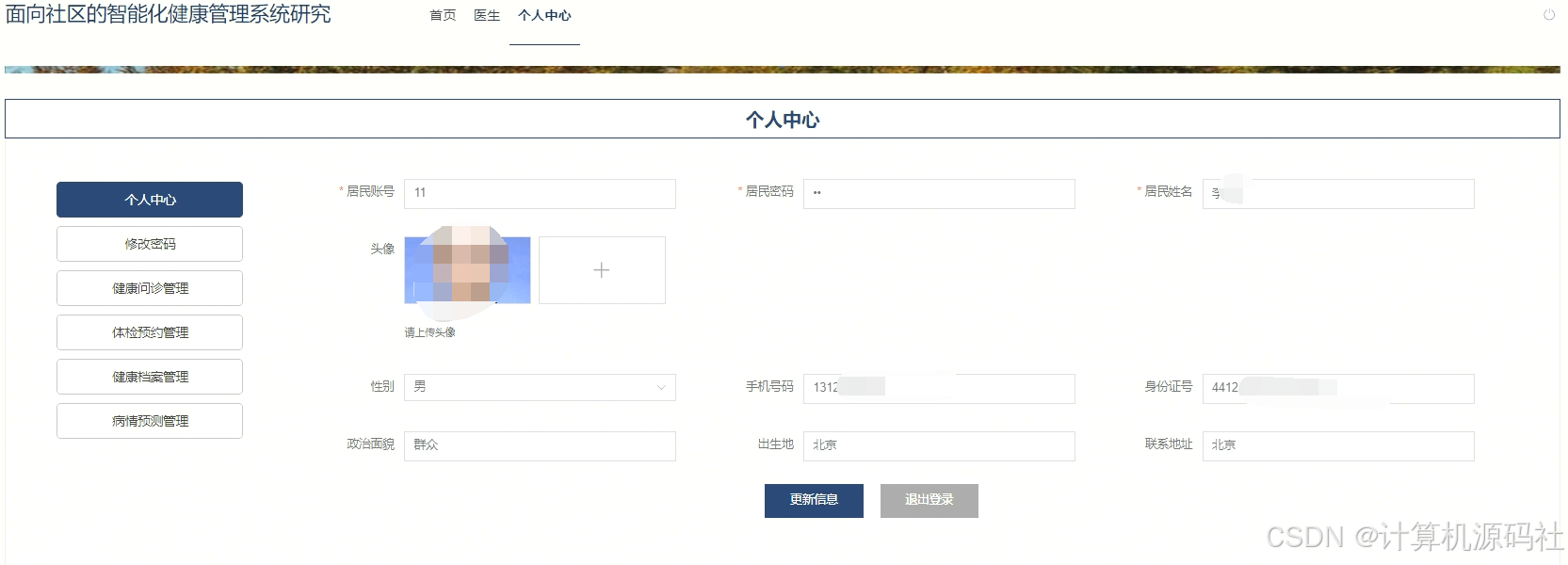
分享一个基于Spring Boot的面向社区的智能化健康管理系统的设计与实现(源码、调试、LW、开题、PPT)
💕💕作者:计算机源码社 💕💕个人简介:本人 八年开发经验,擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等,大家有这一块的问题可以一起交流&…...

【扒代码】reduction参数是什么
model DensityMapRegressor(in_channels256, reduction8)reduction 参数在 DensityMapRegressor 类中用于决定模型在上采样过程中的层级配置。具体来说,它决定了上采样过程中使用多少个 UpsamplingLayer,从而影响输出的分辨率。 reduction 参数的作用 …...
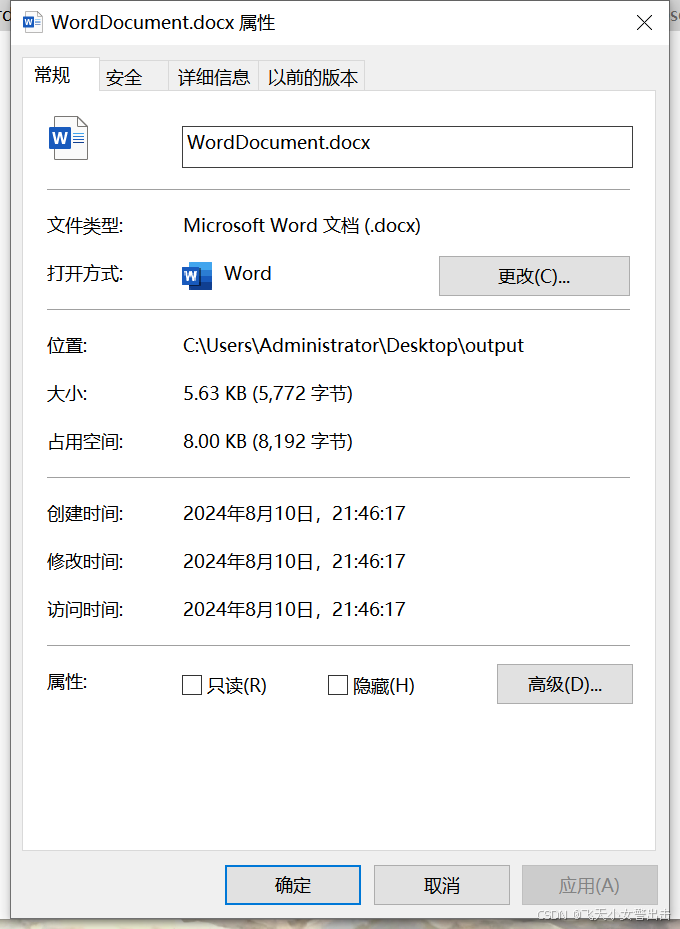
Python,Spire.Doc模块,处理word、docx文件,极致丝滑
Python处理word文件,一般都是推荐的Python-docx,但是只写出一个,一句话的文件,也没有什么样式,就是36K。 再打开word在另存一下,就可以到7-8k,我想一定是python-docx的问题,但一直没…...

redis的安装与命令
一、redis与memcache总体对比 1.性能 Redis:只使用单核,平均每一个核上Redis在存储小数据时比Memcached性能更高。 Memcached:可以使用多核,而在100k以上的数据中,Memcached性能要高于Redis。 2.内存使用效率 Mem…...

【C++】特殊类设计类型转换
目录 💡前言一,特殊类设计1. 请设计一个类,不能被拷贝2. 请设计一个类,只能在堆上创建对象3. 请设计一个类,只能在栈上创建对象4. 请设计一个类,不能被继承5. 请设计一个类,只能创建一个对象(单…...

为git 命令行 设置代理环境变量
http://t.csdnimg.cn/cAxkg 国内需要修改pinoko根目录下gitconfig文件,添加 [http]proxy http://127.0.0.1:1080 [https]proxy https://127.0.0.1:1080或者通过命令行配置: git config --global http.proxy http://127.0.0.1:1080 git config --glo…...

自定义linux某些常见配置
1.当前路径 echo "PS1\u\h:\w\$ " >> /etc/profile source /etc/profile 2.ssh使能 1.开启openssh 2.权限赋予chown root.root /var/empty/ 3.开发板作为server echo "PermitRootLogin yes" >> /etc/ssh/sshd_config 3开机自启动脚本 1.init…...
告别手动操作!KeyMouseGo实现自动化工作流
前言 在这个快节奏的时代,我们每天都在与电脑打交道,重复着那些繁琐而单调的操作;你是否曾想过,能让电脑自己完成这些任务,而你则悠闲地喝着咖啡,享受着生活?今天,就让我们一起揭开一…...

大型语言模型微调 新进展-4篇 论文
1. Brevity is the soul of wit: Pruning long files for code generation 发布时间:2024-06-29链接:https://arxiv.org/abs/2407.00434机构:伦敦大学学院 (UCL) 本研究针对大型语言模型的代码生成任务中的数据清理问题进行了探索。研究发现…...
专业课140+杭电杭州电子科技大学843信号与系统考研经验电子信息与通信工程真题,大纲,参考书。
顺利上岸杭电,由于专业课考的不错140,群里不少同学希望分享一点经验,回头看看这一年考研复习,确实有得有失,总结一下自己的专业课复习经验,希望对大家有帮助,基础课考的没有专业好,而…...
php 中 (0 == ‘abc‘) 为真
https://andi.cn/page/621653.html...
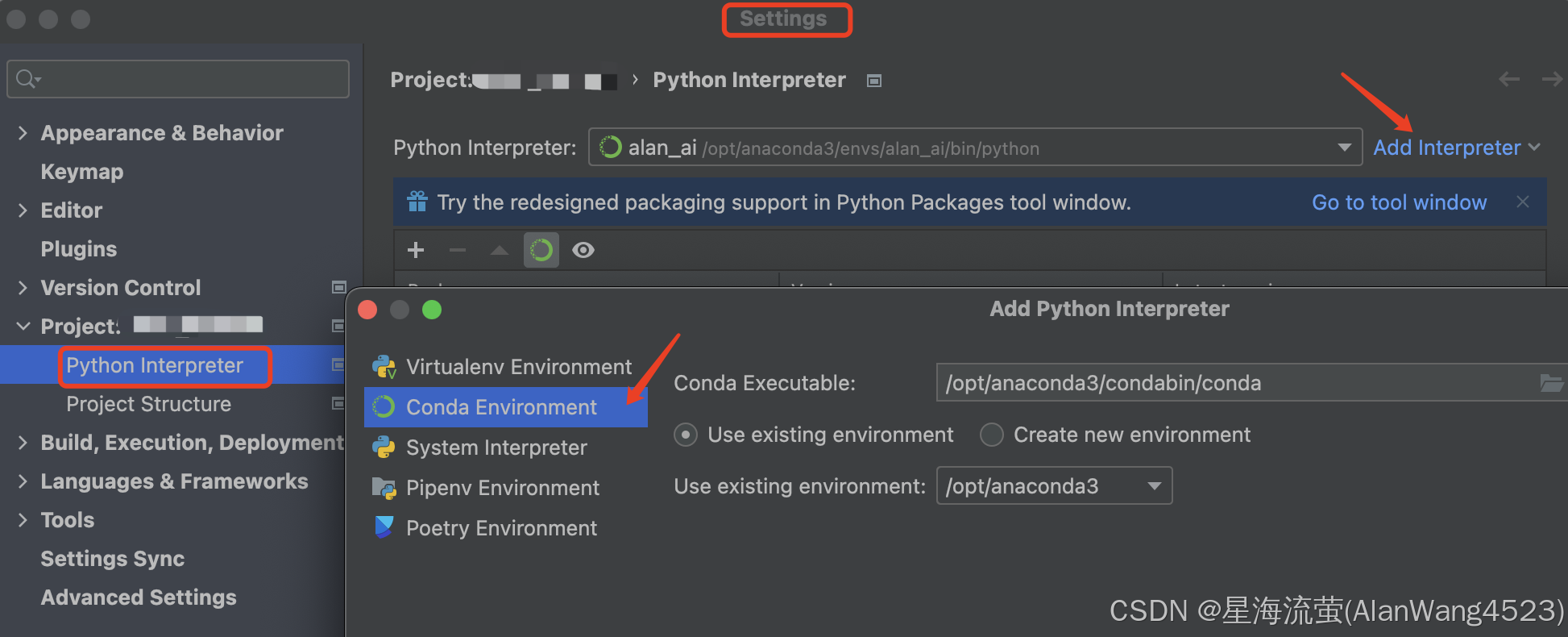
MacOS Anaconda 安装教程及虚拟环境创建
一、下载 Anaconda 1、Anaconda 官网 2、清华大学开源软件镜像站 点 Date 按时间排序,根据自己 Mac 芯片类型下载对应最新版本的。 Intel 芯片的下载 x86_64 版本的Apple m1 芯片的下载 arm64 版本的 二、安装 Anaconda 将安装包下载到本地后,双击安…...

Mac快速配置ADB环境变量
ADB是进行 Androd 开发时很常用的调试工具,Android SDK 中就包含了该工具,所以如果安装了SDK那只需要在环境变量中配置 Android SDK 的路径即可,本文的环境配置也基于这种场景。 如果需要独立下载 ADB 工具,请参考下面网址&#x…...

Kylin的工作原理及使用分享
前言 在当今信息爆炸的时代,企业和研究机构每天都在生成和收集大量的数据。这些数据中蕴藏着巨大的商业价值和研究潜力,但要从中提取出有用的信息却并非易事。传统的数据处理和分析技术在面对如此庞大的数据量时,往往难以提供快速和有效的响…...

python 使用seleniumwire获取响应数据
seleniumwire 是一个在 Selenium WebDriver 基础上扩展的库,它允许你在使用 Selenium 进行网页自动化测试或爬虫时捕获和修改 HTTP 请求和响应。这对于需要分析网页数据或进行更复杂的网络交互的自动化任务特别有用。 以下是如何使用 seleniumwire 来获取响应数据的…...
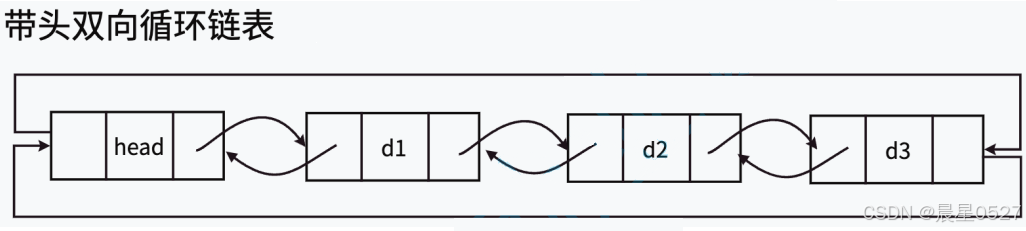
用C语言实现双向链表
目录 一.双向链表的结构 二. 双向链表的实现 1. 在List.h中结构体的定义和各函数的声明 1.1 结构体(节点)的定义 1.2 各函数的声明 2. 在List.c中各函数的实现 2.1 初始化 LTInit 2.2 尾插 LTPushBack 2.3 打印 LTPrint 2.4 头插 LTPushFron…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
