做报表用什么工具?不想再用Excel了!!!
一、什么是中国式报表?
不知道大家现在还是使用Excel来制作报表,然后跟领导汇报工作吗?虽然Excel功能很强大,但是用Excel做过中国式报表的小伙伴一定知道它的制作过程有多复杂。
中国式报表可以用一句话简单概括:格式复杂、信息量大、制作困难的一种报表。
中国式报表制作究竟有多难?一图即可见分晓↓↓↓

如上图,在这份报表里,我们不但要看每个销售人员的每个类别的销售额,而且还要把类别和地区汇总......所以一般都需要用非常专业的工具才能开发中国式报表。
那有没有一种工具,可以做到数据处理与可视化效果兼顾呢?
如今在国内,也有许多做中国式报表的工具了,所以今天我就来为大家介绍几款制作报表的工具,每一款都非常推荐!
二、制作中国式报表的神器来了!
1. 山海鲸报表
山海鲸是一个企业级的报表工具,主打一个“真免费”和“真好用”。
• 免费:无论是个人还是企业,无论用于学习还是商用,都是免费使用的。
• 好用:无需编程基础,大家即可通过简单的拖拽式操作创建报表。
除以上两点外,山海鲸还具有实时数据刷新、支持多数据源接入等特点,这样可以确保报表中的数据始终保持最新状态,减少人为错误。

山海鲸报表提供了丰富的功能组件,在工具的样式中可以设置表头、行格式、列格式、序号列和动画等,还支持自动换行、文字颜色、背景颜色、行高、行间距等自定义设置。并且还有一个非常亮眼的地方,就是它还内置了3D渲染引擎和GIS系统,支持3D数字孪生场景和地理空间的构建和展示,在可视化效果方面简直没得说!
2. Smartbi Spreadsheet
Smartbi主打一个“真Excel”,功能上与Excel高度兼容,可以理解为一种类Excel报表设计器。

Spreadsheet支持主流的关系数据库和大数据平台,主要是通过Excel模板采集数据。既可以支持灵活强大的SQL,也允许使用无代码的方式生成数据集(但是需要先设计业务主题)。工具内支持字体、表格样式、函数、图形、条件格式等,同时提供隐藏、冻结行列等常用功能。
在图形方面,Spreadsheet除了支持Excel静态图形外,还可使用ECharts实现动态图形。它的通过映射规则来实现单元格插入和修改数据的,能同时修改多个数据表,从这一点上来说,这会要求大家有一点编程基础。
3. 润乾报表
润乾报表是一个纯JAVA的企业级报表工具,自称是中国报表的鼻祖。
它提供了灵活的报表设计方式,包括非线性报表模型、强关联语义模型等先进技术,通过鼠标选择和拖拽即可完成复杂的报表制作。

在使用润乾制作报表时,内容数据可以自动缩小填充单元格,同时也支持滚动式报表和多种二维、三维统计图。
但是有一点值得注意,润乾的单套报表价格至少也需要1w,这相对以上两个工具来说费用较高,对于预算有限的企业来说可能是一个考虑因素。
三、总结
中国式报表可以说是复杂的代名词了,所以选择一个合适的报表工具就显得尤为重要,它可以帮助大家更好地理解数据,否则就需要浪费大量的时间和精力,还容易被数据搅得一团乱麻!
不管你以前是通过代码的方式开发报表,还是使用Excel开发离线报表,又或者是使用类Excel传统报表工具,在采用了这些报表工具之后,你都不禁会感慨一句:以前过的都是什么苦日子啊!
好记性不如烂笔头,说再多不如自己上手!欢迎大家使用以上工具后与我交流使用心得噢~
相关文章:

做报表用什么工具?不想再用Excel了!!!
一、什么是中国式报表? 不知道大家现在还是使用Excel来制作报表,然后跟领导汇报工作吗?虽然Excel功能很强大,但是用Excel做过中国式报表的小伙伴一定知道它的制作过程有多复杂。 中国式报表可以用一句话简单概括:格式…...

c++实现学生管理系统(附源码)
目录 一、基本功能: 二、包含的模块: 三、系统介绍 1. 学生管理系统的功能: 2. 具体的需求: 3. 支持的标准: 四、系统结构功能图: 五、系统设计 1. 退出系统: 2. 增加学生:…...

JS防抖是什么?干嘛用的?
你好同学,我是沐爸,欢迎点赞、收藏和关注!个人知乎 防抖在前端开发中可以说经常用到,有诸多使用场景。接下来我们一起看下防抖的定义、防抖函数的实现、应用场景、lodash防抖函数以及防抖在框架中的使用。Let’s go 一、什么是防…...

Linux磁盘管理与文件系统(二):实用工具和命令、fdisk分区示例
文章目录 4、查看或管理磁盘分区-fdisk格式选项示例 4、示例:使用 fdisk 命令创建分区需求操作步骤 5、创建文件系统-mkfs格式常用选项示例创建其他类型的文件系统 6、创建文件系统-mkswap格式常用选项示例拓展:关闭和启用交换分区拓展:swap分…...
)
使用vtkRenderer创建的显示点云的窗口如何刷新(QT/C++)
一、使用vtkRenderer创建点云显示窗口,参考 在Qt创建的UI中放一个显示点云的窗口(PCLQT5)_pcl点云和qt-CSDN博客 二、刷新vtkRenderer创建的窗口 使用场景:在某些情况下代码中需要对显示窗口的显示物改动,例如通过滑…...

Mysql绕过小技巧
上源码。 <?php $mysqli new mysqli("localhost", "root", "root", "security");/* check connection */ if ($mysqli->connect_errno) {printf("Connect failed: %s\n", $mysqli->connect_error);exit(); }$my…...

气象大数据案例项目(求各气象站的平均气温)
气象大数据案例项目(求各气象站的平均气温) 一、项目需求二、数据格式三、项目开发3.1 在windows 进行开发3.2 运行结果3.3 对项目打包 一、项目需求 现在有一份来自美国国家海洋和大气管理局的数据集,里面包含近30年每个气象站、每小时的天…...
」2024年4月19日)
博客摘录「 一个ModBus RTU程序(支持01、02、03、05、06、15、16功能码)」2024年4月19日
发送数据最好改为中断模式,不然通信速度不够。...

Vue3学习笔记第一天
MVVM Vue是一种用于构建用户界面的JavaScript框架。MVVM 是Vue采用的一种软件架构模式,用于构建交互式的用户界面。它的全称是 Model-View-ViewModel,这三个部分分别代表了应用程序的不同层次和角色: Model(模型)&…...

C++之类与对象(完结撒花篇)
目录 前言 1.再探构造函数 2.类型转换 3.static成员 4. 友元 5.内部类 6.匿名对象 7.对象拷贝时的编译器优化 结束语 前言 在前面的博客中,我们对类的默认成员函数都有了一定了解,同时实现了一个日期类对所学的没内容进行扩展延伸,本…...

代码质量的守护者:Python静态代码分析工具的集成之道
标题:代码质量的守护者:Python静态代码分析工具的集成之道 在软件开发过程中,代码质量是至关重要的一环。Python作为一种流行的编程语言,拥有众多的静态代码分析工具,它们能够在代码运行之前检测潜在的错误和代码风格…...

JVM -- 类加载器
类加载器(ClassLoader)是Java虚拟机提供给应用程序去实现访问接口和类字节码数据的技术。类加载器只负责加载过程中的字节码获取并加载到内存的这一过程。 一、 类加载器的分类 类加载器的详细信息可以使用Arthas通过classloader命令查看: 1.启动类加载器(Boots…...

OLAP引擎之StarRocks
StarRocks 是一款新兴的开源分布式实时分析型数据库,专为高性能、高并发的数据分析场景设计。它结合了传统数据仓库和大数据技术的优势,提供了强大的实时数据处理和分析能力。以下是对 StarRocks 的详细介绍,涵盖其基本概念、核心特性、架构设…...

基于微信小程序的小区业主服务系统(源码+论文+部署讲解等)
博主介绍:✌全网粉丝10W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行前辈交流✌ 技术栈介绍:我是程序员阿龙ÿ…...

C++ | Leetcode C++题解之第327题区间和的个数
题目: 题解: class Solution { public:int countRangeSumRecursive(vector<long>& sum, int lower, int upper, int left, int right) {if (left right) {return 0;} else {int mid (left right) / 2;int n1 countRangeSumRecursive(sum,…...

C# Winform 多窗体切换方式一
一、简介 在 Winform 开发中,多窗体的切换是一个常见的需求,比如登录成功后,切换至主界面,在网上查阅相关的资料,你会发现很多都是用 form2.Show(); this.Hide(); 这种方式,这种方式也存在一些问题&#…...

笔记本CPU天梯图(2024年8月),含AMD/骁龙等新CPU
原文地址(高清无水印原图/持续更新/含榜单出处链接): 2024年8月笔记本CPU天梯图 2024年8月笔记本CPU天梯图 2024年8月5日更新日志:常规更新Cinebench R23、PassMark笔记本CPU天梯图,新增Geekbench 6.2单核多核天梯图&…...
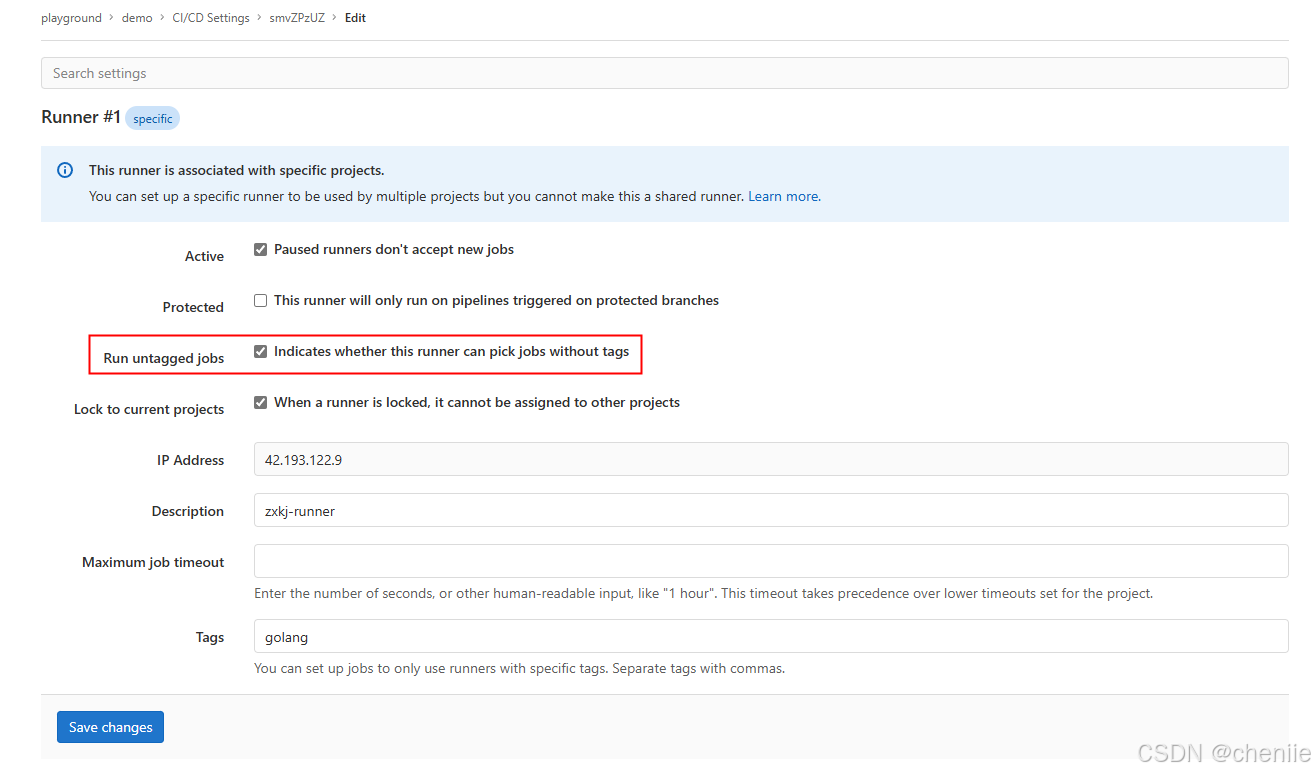
GitLab-CI/CD指南
由于公司没有运维,写go服务时各个环境编译部署还是略显麻烦,由于代码管理使用的是 gitlab,所以决定使用 gitlab 自带的 CI/CD 来做自动编译和部署,这样每次提交代码以后就可以自动部署到服务器上了。 gitlab 本身只有 CI/CD 的接…...

io目录操作学习
1、基本概念 目录也是一种文件,因此操作流程与普通文件类似,有诸如打开、关闭、定位等概念,但目录是一种特殊的文件,目录存储的数据的最小单位并不是字符,而是目录项。这使得目录跟普通文件又有区别。 在Linux中&…...

Ant-Design-Vue
Ant-Design-Vue是蚂蚁金服Ant Design官方推荐的Vue版UI组件库,它继承了Ant Design的设计语言和Vue.js的易用性,为开发者提供了丰富、高质量的Vue组件,极大地简化了前端开发流程。以下是一份详细的Ant-Design-Vue快速上手指南及排坑建议&#…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
