Leetcode - 周赛409
目录
一,3242. 设计相邻元素求和服务
二,3243. 新增道路查询后的最短距离 I
三,3244. 新增道路查询后的最短距离 II
四,3245. 交替组 III
一,3242. 设计相邻元素求和服务

本题纯模拟,代码如下:
class neighborSum {int[][] t;int n, m;public neighborSum(int[][] grid) {n = grid.length;m = grid[0].length;t = grid;}public int adjacentSum(int value) {int x=-1, y=-1;for(int i=0; i<n; i++){for(int j=0; j<m; j++){if(t[i][j] == value){x = i;y = j;break;}}if(x!=-1 && y!=-1) break;}int ans = 0;if(x>0) ans += t[x-1][y];if(y>0) ans += t[x][y-1];if(x+1<n) ans += t[x+1][y];if(y+1<m) ans += t[x][y+1];return ans;}public int diagonalSum(int value) {int x=-1, y=-1;for(int i=0; i<n; i++){for(int j=0; j<m; j++){if(t[i][j] == value){x = i;y = j;break;}}if(x!=-1 && y!=-1) break;}int ans = 0;if(x>0 && y>0) ans += t[x-1][y-1];if(x>0 && y+1<m) ans += t[x-1][y+1];if(x+1<n && y>0) ans += t[x+1][y-1];if(x+1<n && y+1<m) ans+=t[x+1][y+1];return ans;}
}二,3243. 新增道路查询后的最短距离 I

本题每次查询可以使用 bfs 计算出从 0 到 n-1 的最短路径长度,代码如下:
class Solution {public int[] shortestDistanceAfterQueries(int n, int[][] queries) {int t = queries.length;int[] ans = new int[t];List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, e->new ArrayList<>());for(int i=0; i<n-1; i++){g[i].add(i+1);}int k = 0;for(int[] q : queries){g[q[0]].add(q[1]);Queue<Integer> que = new LinkedList<>();boolean[] vis = new boolean[n];vis[0] = true;que.add(0);int cnt = 0;while(!que.isEmpty() && ans[k] == 0){int size = que.size();while(size-- > 0){int poll = que.poll();for(int x : g[poll]){if(!vis[x]){vis[x] = true;que.add(x);if(x == n-1){ans[k] = cnt+1;}}}}cnt++;}k++;}return ans;}
}三,3244. 新增道路查询后的最短距离 II

本题和上一题不同,它多给了一个条件不存在两个查询满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1],也就是说它不会出现两个集合相交的情况。
方法一:
- 可以使用一个有序集合存储每个点,对于每一个查询,我们直接删除在(queries[i][0],queries[i][1])范围内的点,这时的答案就是集合的大小 - 1,代码如下:
class Solution {public int[] shortestDistanceAfterQueries(int n, int[][] queries) {TreeSet<Integer> set = new TreeSet<>();for(int i=0; i<n; i++) set.add(i);int[] ans = new int[queries.length];for(int i=0; i<queries.length; i++){int l = queries[i][0], r = queries[i][1];找到>=l+1的最小的值,使用红黑树实现,时间复杂度O(logn)Integer ceiling = set.ceiling(l+1);//删除(l,r)之间的点while(ceiling != null && ceiling < r){set.remove(ceiling);ceiling = set.ceiling(l+1);}ans[i] = set.size()-1;}return ans;} }方法二:并查集
- 可以把 i -> i + 1 的这段路当成一个点,这时就可以把它当成一个互不相连的图,画个图理解一下:
class Solution {int[] f;int find(int x){if(f[x] != x){f[x] = find(f[x]);}return f[x];}public int[] shortestDistanceAfterQueries(int n, int[][] queries) {f = new int[n];for(int i=1; i<n; i++){f[i] = i;}int[] ans = new int[queries.length];int cnt = n-1;for(int i=0; i<queries.length; i++){int l = queries[i][0] + 1;int r = queries[i][1];int j = find(l), fr = find(r);while(j < fr){//将节点 [l+1, R] 联通 cnt--;f[j] = fr;j = find(j+1);}ans[i] = cnt;}return ans;} }
四,3245. 交替组 III

代码如下:
class Fenwick{int[][] t;public Fenwick(int n){t = new int[n][2];}void update(int size, int op){int i=t.length-size;while(i < t.length){t[i][0] += op;t[i][1] += op*size;i += i & -i;}}int[] query(int size){int cnt = 0, sum = 0;int i = t.length - size;while(i > 0){cnt += t[i][0];sum += t[i][1];i -= i & -i;}return new int[]{cnt, sum};}
}
class Solution {public List<Integer> numberOfAlternatingGroups(int[] colors, int[][] queries) {List<Integer> ans = new ArrayList<>();TreeSet<Integer> set = new TreeSet<>();int n = colors.length;Fenwick f = new Fenwick(n+1);for(int i=0; i<n; i++){if(colors[i] == colors[(i+1)%n]){add(set, f, n, i);}}for(int[] q : queries){if(q[0] == 1){if(set.isEmpty()){ans.add(n);}else{int[] res = f.query(q[1]);ans.add(res[1]-res[0]*(q[1]-1));}}else{int i = q[1];if(colors[i] == q[2]) continue;int pre = (i - 1 + n) % n;int nxt = (i + 1) % n;if(colors[pre] == colors[i]){del(set, f, n, pre);}if(colors[nxt] == colors[i]){del(set, f, n, i);}colors[i] ^= 1;if(colors[pre] == colors[i]){add(set, f, n, pre);}if(colors[nxt] == colors[i]){add(set, f, n, i);}}}return ans;}private void add(TreeSet<Integer> set, Fenwick f, int n, int i){if(set.isEmpty()){f.update(n, 1);}else{update(set, f, n, i, 1);}set.add(i);}private void del(TreeSet<Integer> set, Fenwick f, int n, int i){set.remove(i);if(set.isEmpty()){f.update(n, -1);}else{update(set, f, n, i, -1);}}private void update(TreeSet<Integer> set, Fenwick f, int n, int i, int op){Integer pre = set.floor(i);if(pre == null){pre = set.last();}Integer nxt = set.ceiling(i);if(nxt == null){nxt = set.first();}f.update((nxt-pre+n-1)%n+1, -op);f.update((i-pre+n)%n, op);f.update((nxt-i+n)%n, op);}
}相关文章:

Leetcode - 周赛409
目录 一,3242. 设计相邻元素求和服务 二,3243. 新增道路查询后的最短距离 I 三,3244. 新增道路查询后的最短距离 II 四,3245. 交替组 III 一,3242. 设计相邻元素求和服务 本题纯模拟,代码如下ÿ…...

突破百度网盘的下载限速,两种方法教会你【超详细】
一、前言 Hello,大家后,我是博主英杰,前几天,我在使用百度网盘过程中,下载速度极慢,自己作为一个白嫖党,开会员也是心疼那点钱,所以在网上找了几个有效解决百度网盘限速问题的教程&a…...

整理 酷炫 Flutter 优质 布局、交互 开源App
xtimer-flutter-app Flutter 计时器应用 项目地址:https://github.com/pedromassango/xtimer-flutter-app 项目Demo:https://download.csdn.net/download/qq_36040764/89631382...

【PyCharm怎么同时打开多个项目】
问题描述: 之前点击了“dont ask again”,再也不能同时打开两个或多个项目了。 解决: file->settings->appearance->system settings->project->选择ask...
使用 ProcDump 调试 Linux
Debug Linux using ProcDump By Gaurav Kamathe July 17, 2020 译者:wxy 校对:wxy 微软越来越心仪 Linux 和开源,这并不是什么秘密。在过去几年中,该公司稳步地增加了对开源的贡献,包括将其部分软件和工具移植到 L…...

2023年中国城市统计年鉴(PDF+excel)
2023年中国城市统计年鉴 1、时间:1985-2023年 2、格式:PDFexcel 3、说明:中国城市统计年鉴收录了全国各级城市社会经济发展等方面的主要统计数据,数据来源于各城市的相关部门。本年鉴内容共分四个部分:第一部分是全…...

自用 K8S 资源对象清单 YAML 配置模板手册-1
Linux 常用资源对象清单配置速查手册-1 文章目录 1、Pod 容器集合2、Pod 的存储卷3、Pod 的容器探针4、ResourceQuota 全局资源配额管理5、PriorityClass 优先级类 管理多个资源对象清单文件常用方法: 使用 sed 流式编辑器批量修改脚本键值进行资源清单的创建&am…...

【数据库】事务 | 视图 | 自定义函数创建
1、事物及其特征 事物机制的应用:淘宝订单交易,微信转账等。 视图--------筛子---------过滤-------筛选想要的信息 数据库只存放了视图对应的SQL语句。 视图是一个虚拟的表,本质是一个虚拟的SQL命令集合。 (1)创建…...
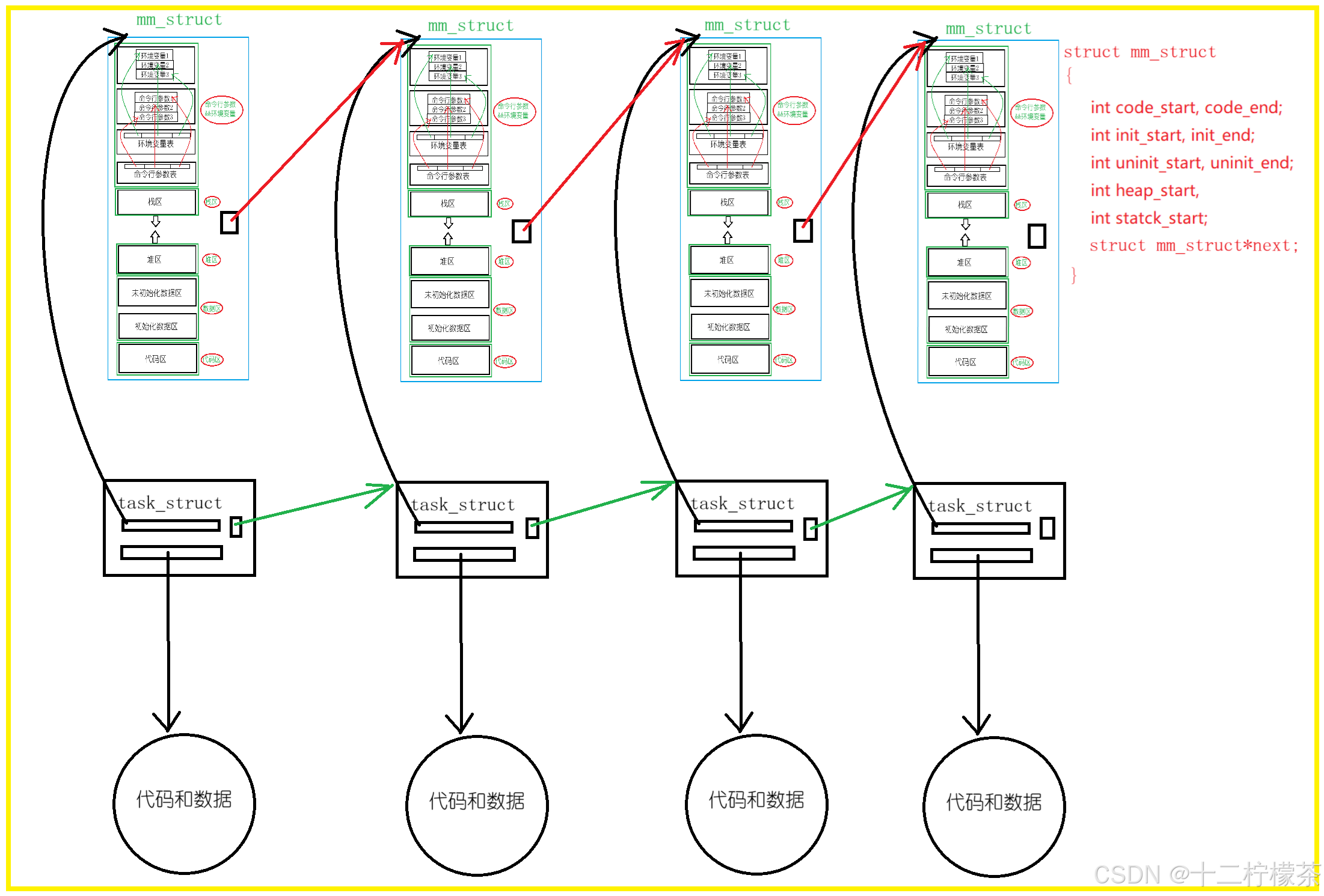
Linux---进程(5)---进程地址空间
目录 预备知识 进程地址空间 什么是进程地址空间 为什么要存在进程地址空间和页表 缺页中断 预备知识 我们在学习语言的时候,一般都会了解到内存区域划分,下面了解一下Linux的内存区域划分。 通过上图,我们了解到 1、堆区向上增长&…...

C语言实现数据结构之队列
目录 队列一. 队列的概念及结构二. 队列的实现1. 要实现的功能2 具体的实现2.1 结构体2.2 初始化2.3 入队列2.4 出队列2.5 返回队首元素2.6 返回队尾元素2.7 队列元素个数2.8 队列判空2.9 队列销毁 三. 队列相关OJ题设计循环队列用队列实现栈用栈实现队列 四. 概念选择题五. 参…...

写一个Vue2和vue3的自定义指令(以复制指定作为示例)
文章目录 一、自定义指令是什么?二、自定义指令有啥用?三、自定义指令怎么用?1.自定义指令的参数2.自定义指令的钩子函数(1)五个钩子函数的说明(2)钩子函数的参数(主要参数:el和valu…...

MySQL —— 聚合查询,分组查询 与 联合查询
聚合函数 常见的统计总数、计算平局值等操作,可以使用聚合函数来实现,常见的聚合函数有: 函数说明count()统计数据总数sum()求和avg()求平均值max()求最大值min()求最小值 注意凡是涉及运算的,数据库会自动掉 NULL 值 注意NULL …...

Spring声明式事务失效场景
Spring声明式事务失效场景 背景搭建测试环境测试事务失效场景Transactional 注解标注在 private 方法上异常被 catch 了,事务失效方法抛出的是受检异常,事务也会失效事务传播行为配置不合理导致事务失效 背景 Spring 针对 Java Transaction API (JTA)、…...

基于SpringBoot+UniAPP宠物食品外卖点单小程序的设计与实现》
✅博主简介:Java 全栈开发工程师,抖音优质技术创作者,日常分享实用的前端、后端、运维开发技术。 ✅技术栈:Java、SpringBoot、Vue、React、Node.js、Nest.js、Nuxt.js、uni-app ✅技术擅长:计算机毕设选题、开题报告、…...

ssrf 内网访问 伪协议 读取文件 端口扫描
SSRF(Server-Side Request Forgery,服务器侧请求伪造)是一种利用服务器发起网络请求的能力来攻击内网资源或执行其他恶意活动的技术。SSRF可以用于访问通常不可由外部直接访问的内网资源,读取文件,甚至进行端口扫描。以…...

发布包到npm
目录 注册npm账号 创建包 登录npm 上架包 更新包 删除包 注册npm账号 首先注册npm账号:npm | Sign Up (npmjs.com) 创建包 可以在桌面上新建一个文件夹:文件夹名随便起,但是别跟npm已经上架的包名重复了 可以通过下面的指令查看&…...

Python | Leetcode Python题解之第324题摆动排序II
题目: 题解: def quickSelect(a: List[int], k: int) -> int:seed(datetime.datetime.now())shuffle(a)l, r 0, len(a) - 1while l < r:pivot a[l]i, j l, r 1while True:i 1while i < r and a[i] < pivot:i 1j - 1while j > l an…...
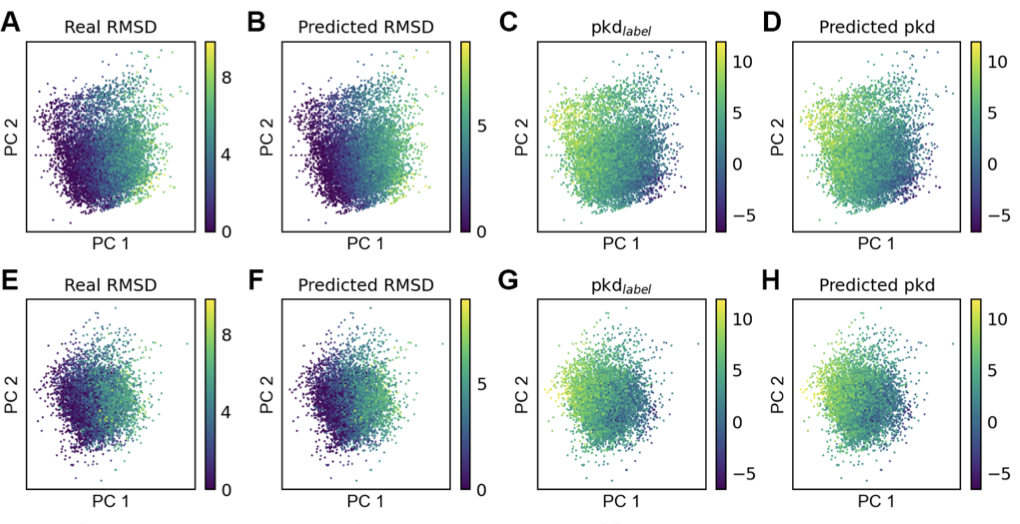
IGModel——提高基于 GNN与Attention 机制的方法在药物发现中的实用性
导言 深度学习在药物发现(发现治疗药物)领域的应用以及传统方法面临的挑战。 药物(尤其是我们将在本文中讨论的被称为抑制剂的药物)通过与在人体中发挥不良功能的蛋白质结合并改变这些蛋白质的功能来发挥治疗效果。因此…...

AArch64中的寄存器
目录 通用寄存器 其他寄存器 系统寄存器 通用寄存器 大多数A64指令在寄存器上操作。该架构提供了31个通用寄存器。 每个寄存器可以作为64位的X寄存器(X0..X30)使用,或者作为32位的W寄存器(W0..W30)使用。这两种是查…...
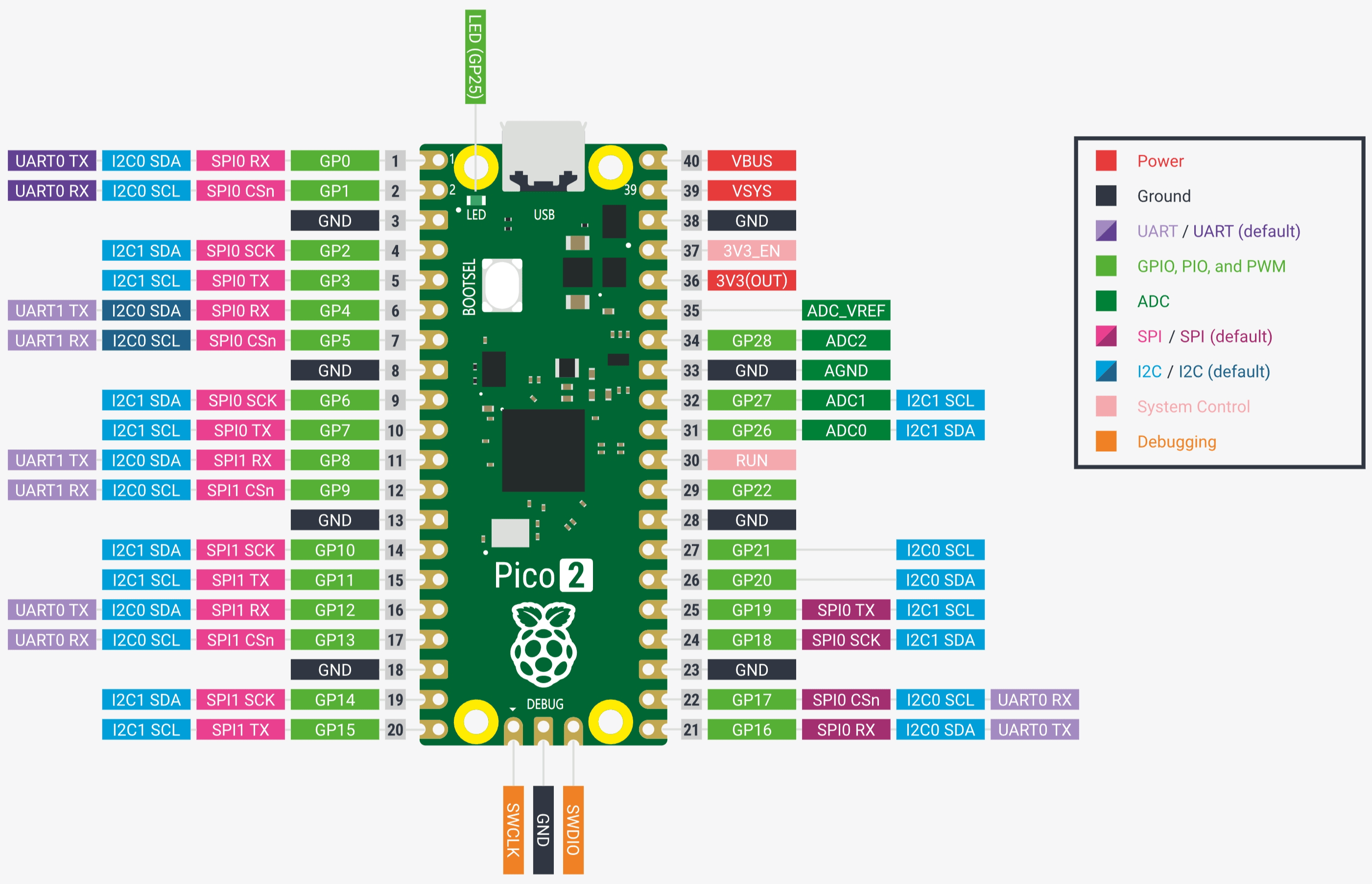
树莓派Pico 2来了
这两天开源圈的大事之一,就是树莓派基金会发布了树莓派Pico 2。 帖子原文:Raspberry Pi Pico 2, our new $5 microcontroller board, on sale now 总结一些关键信息: 产品发布:Raspberry Pi Pico 2 是 Raspberry Pi 基金会推出的…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

