【解答】洛必达法则的使用条件及常见错误,洛必达法则的适用条件,常见的易错点,2022数一第一题例题

目录
洛必达法则的使用条件及常见错误
洛必达法则的适用条件
常见的易错点
举例说明(见D选项)
总结

🌈 嗨,我是命运之光!
🌌 2024,每日百字,记录时光,感谢有你,携手前行~
🚀 携手启航,我们一同深入未知的领域,挖掘潜能,让每一步成长都充满意义。
洛必达法则的使用条件及常见错误
在求解未定式极限时,洛必达法则是一个常用且有效的方法。然而,它的使用并非无条件的。许多人在应用洛必达法则时,忽视了必要的前提条件,导致了错误的结论。本文将简洁清楚地阐述洛必达法则的使用条件,并指出常见的易错点。
洛必达法则的适用条件
要使用洛必达法则,必须满足以下三个条件:
- 未定式形式:分子和分母的极限都必须为 0 或同时趋向于无穷大,即极限形式为
或
。
- 可导性:在所讨论的邻域内,分子和分母函数都必须是可导的,且导数存在。
- 导数之比的极限存在:分子和分母导数之比的极限存在,或为无穷大。
只有在以上三个条件都满足的情况下,才能正确地使用洛必达法则来求解极限。
常见的易错点
一个常见的误解是,仅仅因为极限存在,就可以使用洛必达法则。这是不正确的。只有在分子分母的极限同时为 0 或无穷大时,洛必达法则才适用。否则,使用洛必达法则是错误的。
举例说明(见D选项)
因为f(x)不一定可导,所以不能用洛必达

总结
洛必达法则是一种强有力的工具,用于处理未定式极限,但它并非万能。在使用之前,必须确认分子和分母的极限形式为 或
,且分子和分母在相应的邻域内可导,并且导数之比的极限存在。如果这些条件不满足,洛必达法则不适用,必须考虑其他求极限的方法。掌握这些前提条件,有助于避免在求解极限问题时的错误应用。
嗨,我是命运之光。如果你觉得我的分享有价值,不妨通过以下方式表达你的支持:👍 点赞来表达你的喜爱,📁 关注以获取我的最新消息,💬 评论与我交流你的见解。我会继续努力,为你带来更多精彩和实用的内容。
点击这里👉 ,获取最新动态,⚡️ 让信息传递更加迅速。


相关文章:

【解答】洛必达法则的使用条件及常见错误,洛必达法则的适用条件,常见的易错点,2022数一第一题例题
目录 洛必达法则的使用条件及常见错误 洛必达法则的适用条件 常见的易错点 举例说明(见D选项) 总结 🌈 嗨,我是命运之光! 🌌 2024,每日百字,记录时光,感谢有你&…...

使用Python下载飞书共享表格数据教程
写在前面 随着企业协作办公软件的流行,飞书以其高效的协作能力和便捷的共享功能,成为了许多公司必备的工具之一。在日常工作中,我们经常需要从飞书中下载共享的表格数据进行分析。本文将详细介绍如何使用Python下载飞书共享表格数据。 前置…...

【C++】protobuf的简单使用(通讯录例子)
protobuf的简单使用(通讯录例子) .proto文件的编写保留字段字段唯一编号protobuf的类型enum类型Any类型oneof类型map类型完整通讯录代码.proto文件write文件read文件运行结果 .proto文件的编写 syntax用于指定protobuf的语法;package当.prot…...

Apple 智能基础语言模型
Introducing Apple’s On-Device and Server Foundation Models technical details June 10, 2024 在2024年的全球开发者大会上,苹果推出了Apple Intelligence,这是一个深度集成到iOS 18、iPadOS 18和macOS Sequoia中的个人智能系统。Apple Intelligen…...

GreptimeDB融资数百万美元; Oracle提供免费长期MySQL; 谷歌大模型支持云数据库问题洞察
重要更新 1. 开源时序数据库 GreptimeDB宣布完成数百万美元的新一轮融资。GreptimeDB是一款Rust 语言编写的时序数据库,具有分布式,开源,云原生,兼容性强等特点,帮助企业实时读写、处理和分析时序数据的同时࿰…...

Java中的抽象类与接口
1. 抽象类 1.1 抽象类概念 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的, 如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。 比如&…...

云计算概念以及与云服务的区别
目录 1.云的概念 1.1 什么是云? 1.2 云计算的类型 1.3 云计算的服务模式 1.4 云计算的优势 2.云计算和云服务的区别 2.1 定义 2.2 范围 2.3 角色 2.5 举例 2.6使用者 3.总结 1.云的概念 1.1 什么是云? “云”在计算机科学和信息技术领域通常…...

Netty技术全解析:LengthFieldBaseFrameDecoder类深度解析
❃博主首页 : 「码到三十五」 ,同名公众号 :「码到三十五」,wx号 : 「liwu0213」 ☠博主专栏 : <mysql高手> <elasticsearch高手> <源码解读> <java核心> <面试攻关> ♝博主的话 :…...
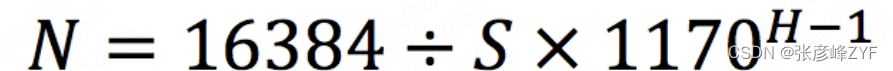
深入InnoDB核心:揭秘B+树在数据库索引中的高效应用
目录 一、索引页与数据行的紧密关联 (一)数据页的双向链表结构 (二)记录行的单向链表结构 二、未创建索引情况 (一)无索引下的单页查找过程 以主键为搜索条件 以非主键列为搜索条件 (二…...

c++(面向对象的性质:抽象,封装,继承,多态)
ctrla全选,ctrli对齐 ctrl/ 一起注释 ctrlz 退回上一步 一些基础的内容: cout:输出流对象 cin:输入流对象 输入一个i和一个j,然后输出ij的和: 值不变的原因: 值传递,a和i是…...

java基础学习笔记1
Java编程规范 命名风格 1. 【强制】代码中的命名均不能以下划线或美元符号开始,也不能以下划线或美元符号结束。 反例:_name / __name / $name / name_ / name$ / name__ 2. 【强制】代码中的命名严禁使用拼音与英文混合的方式,更不允许直…...

[VBA]使用VBA在Excel中 操作 形状shape 对象
excel已关闭地图插件,对于想做 地图可视化 的,用形状来操作是一种办法,就是要自行找到合适的 地图形状,修改形状颜色等就可以用于 可视化展示不同省市销量、人口等数据。 引言 在Excel中,通过VBA(Visual Basic for Applications)可以极大地增强数据可视化和报告自动化…...

Apache POI 实现 Excel 表格下载
这里以苍穹外卖中数据导出功能为例,记录下 Apache POI 导出 Excel 表格的过程。 首先在 pom.xml 中导入相关依赖 <!-- poi 用于操作 excel 表格--> <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId&…...
)
大华嵌入式面试题大全及参考答案(2万字长文)
目录 在C语言中,static 关键字有哪些主要用途? static 修饰的全局变量与普通全局变量有什么区别? 为什么要在嵌入式系统中使用 static 修饰函数? 虚函数与纯虚函数了解么? strcpy 给你加结束符吗,还是要自己加? select 的作用是什么,它和 epoll 的区别? map 与…...

C语言——查漏补缺
前言 本篇博客主要记录一些C语言的遗漏点,完成查漏补缺的工作,如果读者感兴趣,可以看看下面的内容。都是一些小点,下面进入正文部分。 1. 字符汇聚 编写代码,演示多个字符从两端移动,向中间汇聚 #inclu…...

Python | Leetcode Python题解之第328题奇偶链表
题目: 题解: class Solution:def oddEvenList(self, head: ListNode) -> ListNode:if not head:return headevenHead head.nextodd, even head, evenHeadwhile even and even.next:odd.next even.nextodd odd.nexteven.next odd.nexteven even…...

吉瑞外卖笔记
1.项目整体搭建 这里用到的是springboot3mybatisplus 1.1数据库搭建 整体表搭建,这里我是直接用的老师给的数据库 1.2maven项目搭建 依赖 这两个jar包第一次用,记录一下 fastjson json处理,可将对象转化为json形式 可将对象中的属性…...

Perl套接字编程指南:构建网络通信应用
摘要 Perl是一种功能强大的脚本语言,广泛应用于系统管理、网络编程等多种场景。Perl的套接字编程能力允许开发者创建客户端和服务器端的网络应用。本文将详细介绍Perl中套接字的使用,包括基础概念、API的使用,以及构建简单客户端和服务器的示…...

达梦数据库(十) -------- mybatis-plus 整合达梦时,自动生成的 sql 语句报错
一丶【问题描述】: mybatis-plus 整合达梦时,应用系统项目的 sql 语句中包含数据库关键字,导致 mybatis-plus 自动生成的 sql 语句会报错,如下图所示: 二丶【问题解决】: 问题原因:mybatis-pl…...

停止项目大小调整,开始搜索层自动缩放!
作者:来自 Elastic Matteo Piergiovanni,John Verwolf 我们新的 serverless 产品的一个关键方面是允许用户部署和使用 Elastic,而无需管理底层项目节点。为了实现这一点,我们开发了搜索层自动扩展,这是一种根据我们将在…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
