[数据结构]直接插入排序、希尔排序
文章目录
- 排序的概念和运用
- 排序的概念
- 排序运用
- 常见的排序算法
- 常见的排序算法
- 直接插入排序
- 希尔排序
- 性能对比
排序的概念和运用
排序的概念
-
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
-
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
-
内部排序:数据元素全部放在内存中的排序。
-
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
排序运用
在生活中,排序有很多运用,比如说购物按照价格排序,全国高校排序等等
常见的排序算法
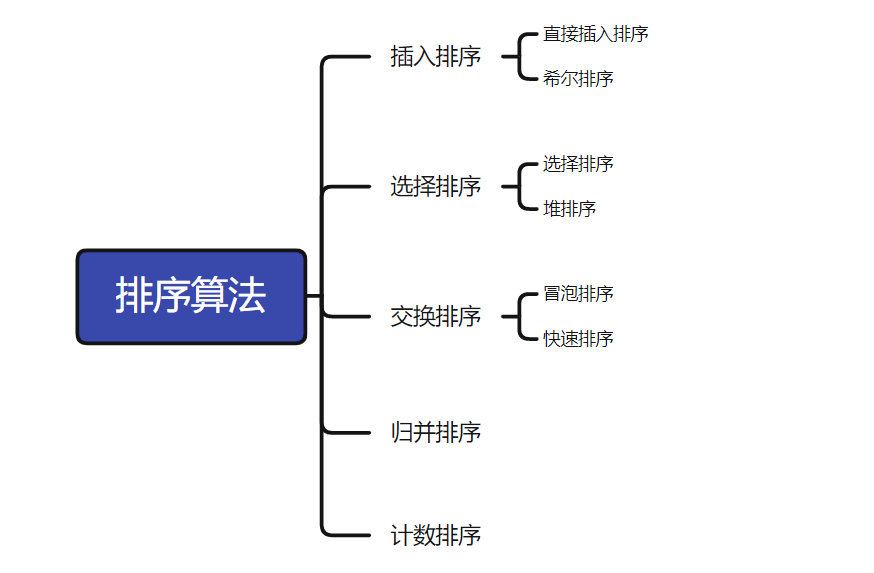
- 插入排序:直接插入排序,希尔排序
- 选择排序:选择排序,堆排序
- 交换排序:冒泡排序,快速排序
- 归并排序
- 计数排序
常见的排序算法
// 常见排序算法接口
// 插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);// 选择排序
void SelectSort(int* a, int n);// 堆排序
void HeapSort(int* a, int n);// 冒泡排序
void BubbleSort(int* a, int n);// 快速排序
void QuickSort(int* a, int left, int right);// 归并排序
void MergeSort(int* a, int n);// 计数排序
void ConutSort(int* a, int n);// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 10000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);
}直接插入排序
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
这和在现实生活中我们玩扑克牌很像,我们在整理牌的时候,每一次拿一张牌插入之前已经有序的牌中,一直整理到最后一张,让整体的牌有序。

动图演示:

参考代码:
// 直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){int end = i;int x = a[end + 1];while (end >= 0){if (a[end] > x){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = x;}
}
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度: O(N^2)
- 空间复杂度: O(1)
- 稳定性:稳定
直接插入排序的时间复杂度进行分析,可以得出一下结论:
- 普通插入排序的时间复杂度最坏情况下为O(N^2),此时待排序列为逆序,或者说接近逆序。
- 普通插入排序的时间复杂度最好情况下为O(N),此时待排序列为升序,或者说接近升序。
希尔排序
希尔排序法又称缩小增量法。
希尔排序法的基本思想是: 先选定一个整数为gap,把待排序文件中所有记录分成个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后缩小gap的值,重复上述分组和排序的工作。当到达gap=1时(相当于直接插入排序),因为此时序列经过了分组预排序,序列的数据已经接近有序,此时再进行直接插入排序,时间复杂度相当于O(N),所有记录在统一组内排好序。
动图演示:

参考代码:
void ShellSort(int* a, int n)
{// 1. 分组预排序 gap > 1// 2. 整体插入排序 gap = 1int gap = n;while (gap > 1){gap = gap / 2;for (int i = 0; i < n - gap; ++i){int end = i;int x = a[end + gap];while (end >= 0){if (a[end] > x){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = x;}}
}
希尔排序的特性总结:
-
希尔排序是对直接插入排序的优化。
-
当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。
-
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,很多书给出了不同的时间复杂度,平均时间复杂度O(N^1.3):
《数据结构(C语言版)》 — 严蔚敏

《数据结构-用面相对象方法与C++描述》 — 殷人昆

-
稳定性:不稳定
性能对比
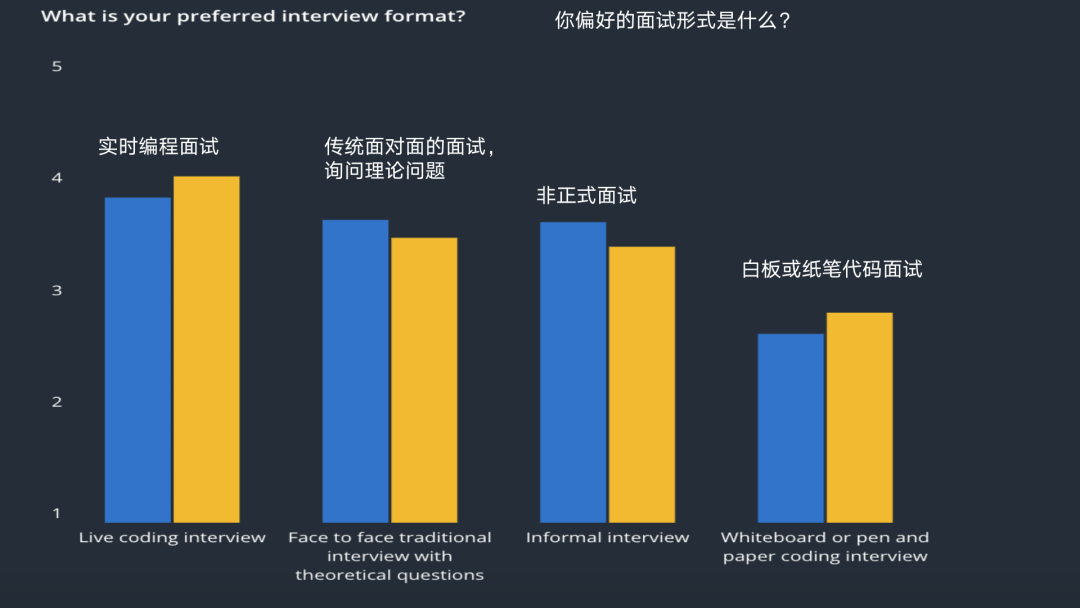
使用直接插入排序和希尔排序进行十万个随机数排序:
测试程序:
// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);free(a1);free(a2);}
测试结果:
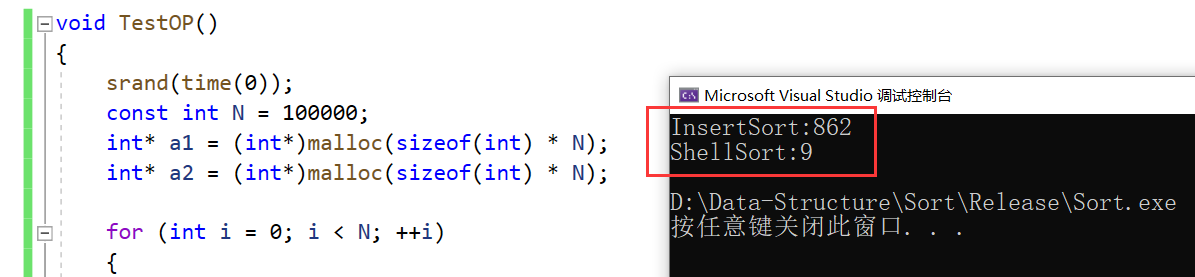
可以看到,希尔排序对于直接插入排序的优化很明显。
相关文章:

[数据结构]直接插入排序、希尔排序
文章目录排序的概念和运用排序的概念排序运用常见的排序算法常见的排序算法直接插入排序希尔排序性能对比排序的概念和运用 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操…...

CNN、LeNet、AlexNet、VGG、GoogLeNet、RCNN、Fast RCNN、Faster RCNN、YOLO、YOLOv2、SSD等的关系
卷积神经网络的现状1943年美国数学家提出人工智能1949年心理学家建立神经元模型1957年弗兰克提出 感知器人工神经网络模型1980年建立多层感知器模型1984日本学者提出卷积神经网络原始模型神经感知机1998年提出LeNet-5卷积神经网络,并发展了其在音符和字符上的优势20…...
)
IO-day1-(fscanf、fprintf.........)
作业一、有一个usr.txt的文件,其中存储着用户的账户和密码,格式如下:zhangsan aaaalisi bbbbb空格前面是账户,空格后面是密码,一行一个账户、密码要求如下:从终端获取一个账户名和密码判断是否能够登录成功…...
C++类和对象(上篇)
目录 1.类的定义 2.类的访问限定符及封装 2.1类的访问限定符 2.2封装 3.类的作用域 4.类的实例化 5.类的大小 6.this 指针 1.类的定义 class className {// 类体:由成员函数和成员变量组成}; // 一定要注意后面的分号 class为定义类的关键字,Clas…...
解决Xshell无法连接Kali Linux 2020.1(2019.3)版本
使用Xshell远程终端工具连接虚拟机的Kali Linux却提示连接不上原因:Kali Linux默认没有打开SSH远程登录,SSH就是一种网络协议,用于加密的远程登录,所以在没有打开SSH协议之前是无法使用Xshell连接Kali Linux的。解决办法ÿ…...
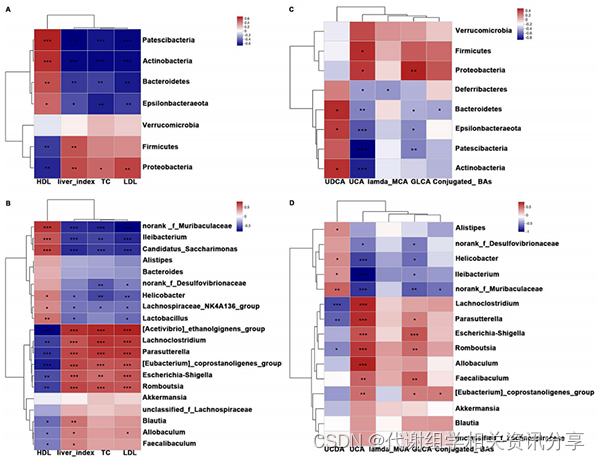
项目文章 | 缓解高胆固醇血症 ,浒苔多糖如何相助?
文章标题:Polysaccharides from Enteromorpha prolifera alleviate hypercholesterolemia via modulating the gut microbiota and bile acid metabolism 发表期刊:Food & Function 影响因子:6.317 作者单位:福建医科大…...
Linux使用宝塔面板搭建网站,并内网穿透实现公网访问
文章目录前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4.固定http地址5. 配置二级子域名6.创建一个测试页面前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...
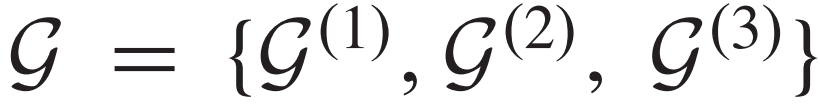
基于深度学习方法与张量方法的图像去噪相关研究
目录 1 研究现状 1.1 基于张量分解的高光谱图像去噪 1.2 基于深度学习的图像去噪算法 1.3 基于深度学习的高光谱去噪 1.4 小结 2 基于深度学习的图像去噪算法 2.1 深度神经网络基本知识 2.2 基于深度学习的图像去噪网络 2.3 稀疏编码 2.3.1 传统稀疏编码 2.3.2 群稀…...
Java基础知识之HashMap的使用
一、HashMap介绍 HashMap是Map接口的一个实现类(HashMap实现了Map的接口),它具有Map的特点。HashMap的底层是哈希表结构。 Map是用于保存具有映射关系的数据集合,它具有双列存储的特点,即一次必须添加两个元素…...

面试--每日一经
操作系统 死锁 死锁:是指两个或两个以上的进程在执行过程中,由于竞争资源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推进下去。 死锁的四个必要条件 互斥条件:一个资源每次只能被一个进…...
JavaSE进阶之(十六)枚举
十六、枚举16.1 背景16.2 枚举类型16.3 EnumSet 和 EnumMap01、EnumSet02、EnumMap16.1 背景 在 Java 语言中还没有引入枚举类型之前,表示枚举类型的常用模式是声明一组 int 类型的常量,常常用的就是: public static final int SPRING 1; …...

全同态加密:TFHE
参考文献: Cheon J H, Stehl D. Fully homomophic encryption over the integers revisited[C]//Advances in Cryptology–EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, …...

【计算机二级】综合题目
计算机二级python真题 文章目录计算机二级python真题一、《大学慕课 两问 》二、综合应用题——价值链三、基本操作题 ——信息输出一、《大学慕课 两问 》 附件中的文件data.txt 是教育部爱课程网中国大学MOOC平台的某个 HTML页面源文件,里面包含了我国参与MOOC建设的一批大学…...
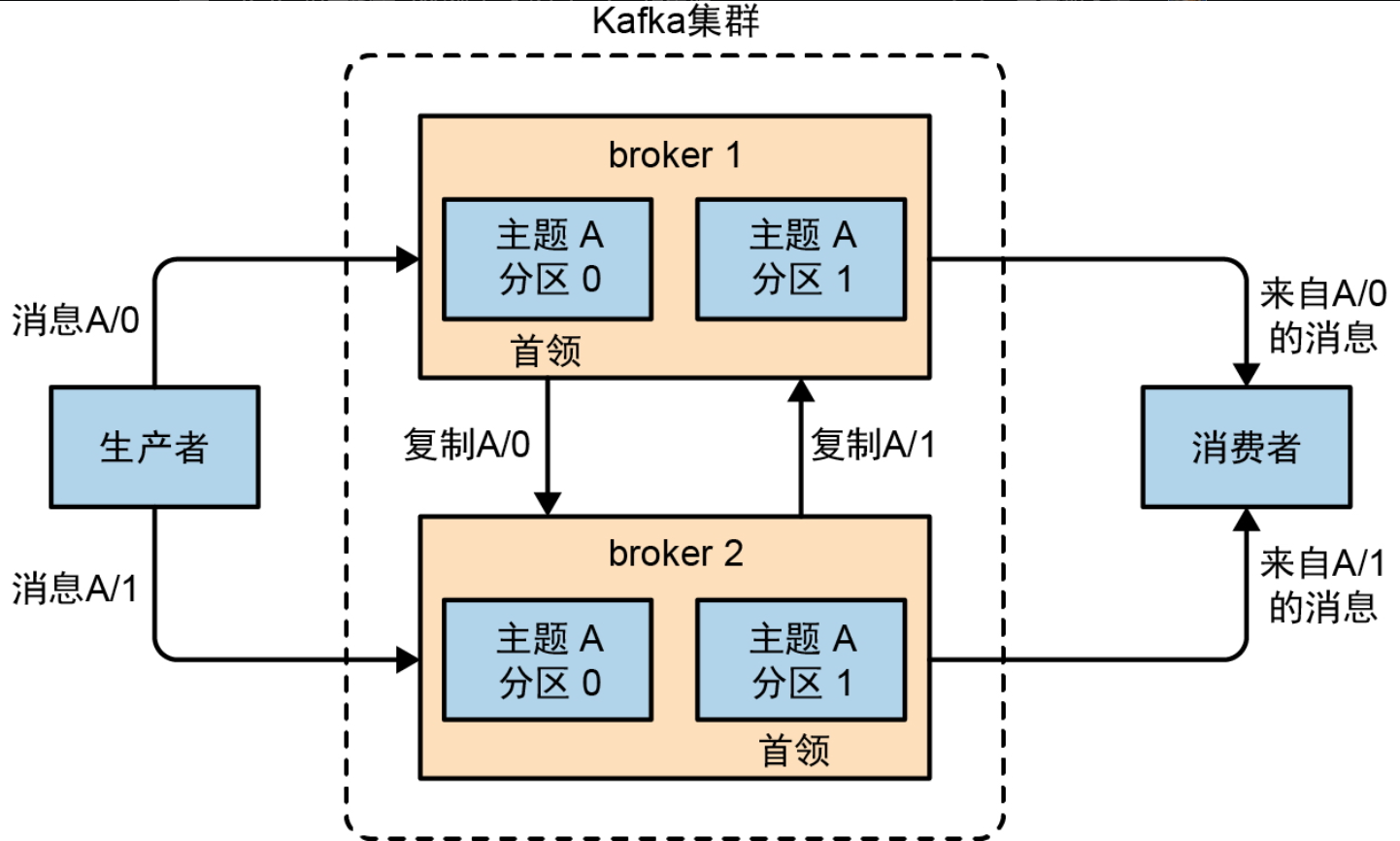
初识Kafka
介绍 Kafka Kafka 是一款基于发布与订阅的消息系统。 用生产者客户端 API 向 Kafka 生产消息,用消费者客户端 API 从 Kafka 读取这些消息。 Kafka 使用 Zookeeper 保存元数据信息。 Kafka 0.9 版本之前,除了 broker 之外, 消费者也会使用…...

【JavaEE】线程的状态
哈喽,大家好~我是保护小周ღ,本期为大家带来的是 Java 多线程的 线程的状态,New 新建状态,Runnable 运行状态,Blocked 阻塞状态,waiting 等待状态,Time_Waiting 超时等待状态,Termin…...
7个最受瞩目的 Python 库,提升你的开发效率
当今时代,数据分析和处理已经成为了各行各业中不可或缺的一环。Python作为一种非常流行的编程语言,为我们提供了许多强大的工具和库来处理不同类型的数据。 在这篇文章中,我将向您介绍七个非常有用的Python库,这些库各自有着独特…...
这些IT行业趋势,将改变2023
上一周,你被"AI"刷屏了吗? 打开任何一家科技媒体,人工智能都是不变的热门话题。周初大家还在用ChatGPT写论文、查资料、写代码,到周末的时候大家已经开始用GPT-4图像识别来做饭、Microsoft 365 Copilot 来写PPT了。 GP…...
蓝桥杯每日一真题——[蓝桥杯 2021 省 B] 杨辉三角形(二分+规律)
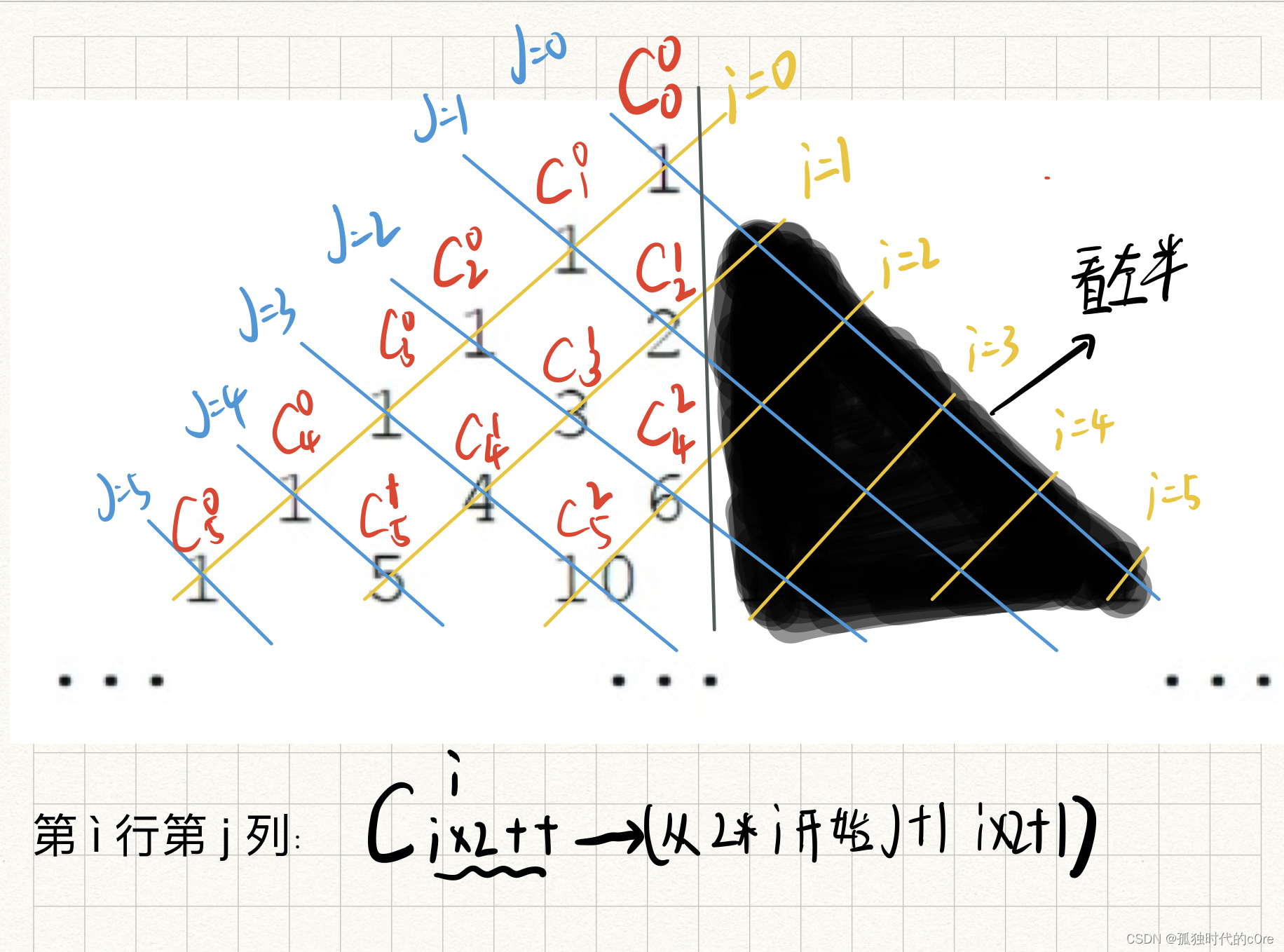
文章目录[蓝桥杯 2021 省 B] 杨辉三角形题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路:全部代码:[蓝桥杯 2021 省 B] 杨辉三角形 题目描述 下面的图形是著名的杨辉三角形: 如果我们按从上到下、从左到右的顺序把所有数排成一列&…...
<C++> 类和对象(下)
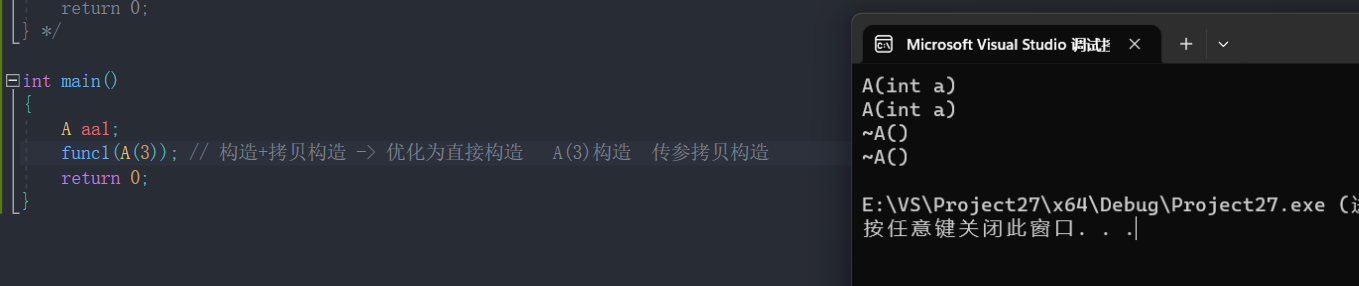
1.const成员函数将const修饰的“成员函数”称之为const成员函数,const修饰类成员函数,实际修饰该成员函数隐含的this指针,表明在该成员函数中不能对类的任何成员进行修改。class A { public:void Print() //这里隐藏了A* this指针{cout <…...
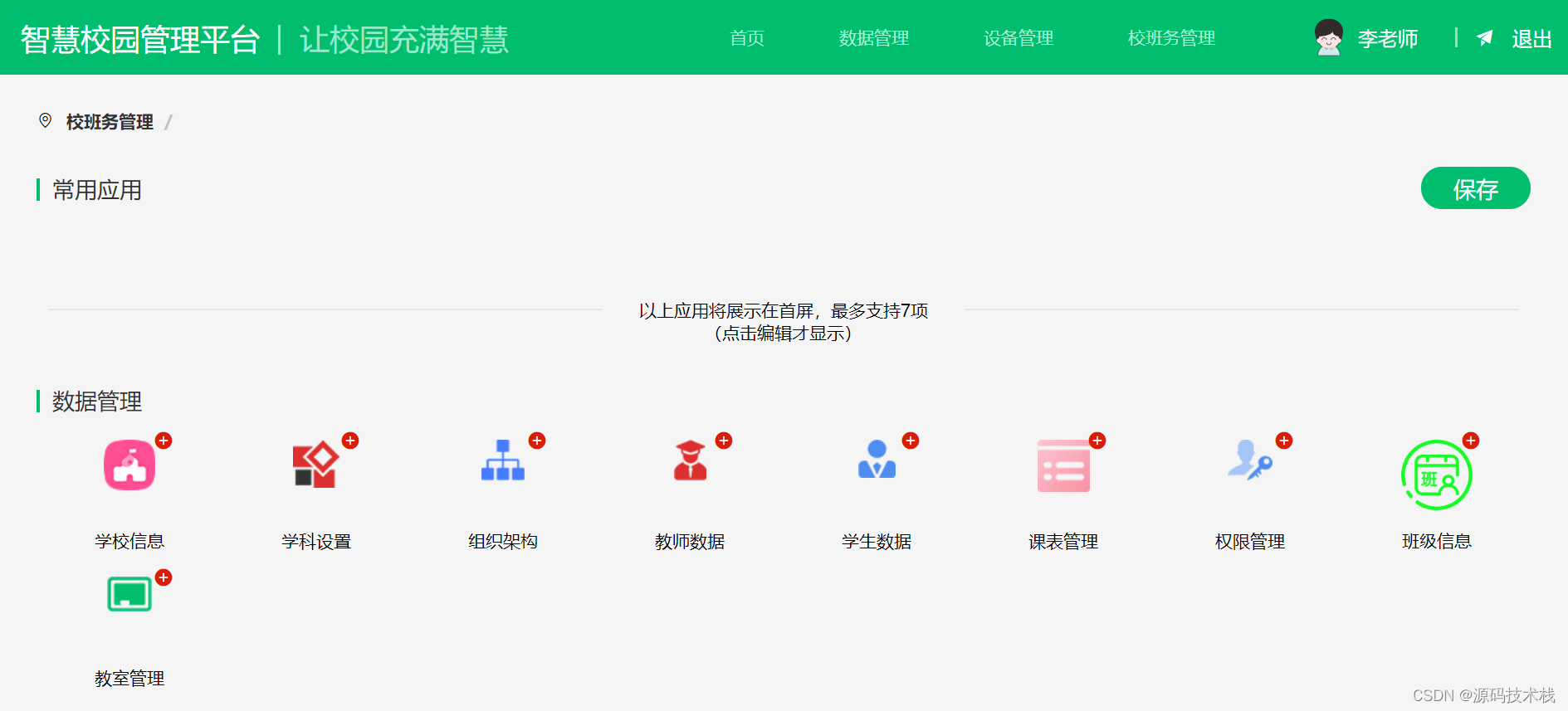
基于Springboot+Vue2前后端分离框架的智慧校园系统源码,智慧学校源码+微信小程序+人脸电子班牌
▶ 智慧校园开发环境: 1、使用springboot框架Javavue2 2、数据库MySQL5.7 3、移动端小程序使用小程序原生语音开发 4、电子班牌固件安卓7.1;使用Java Android原生 5、elmentui ,Quartz,jpa,jwt 智慧校园结构导图▶ 这…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...

el-amap-bezier-curve运用及线弧度设置
文章目录 简介示例线弧度属性主要弧度相关属性其他相关样式属性完整示例链接简介 el-amap-bezier-curve 是 Vue-Amap 组件库中的一个组件,用于在 高德地图 上绘制贝塞尔曲线。 基本用法属性path定义曲线的路径,可以是多个弧线段的组合。stroke-weight线条的宽度。stroke…...

STL 2迭代器
文章目录 1.迭代器2.输入迭代器3.输出迭代器1.插入迭代器 4.前向迭代器5.双向迭代器6.随机访问迭代器7.不同容器返回的迭代器类型1.输入 / 输出迭代器2.前向迭代器3.双向迭代器4.随机访问迭代器5.特殊迭代器适配器6.为什么 unordered_set 只提供前向迭代器? 1.迭代器…...
