全同态加密:TFHE
参考文献:
- Cheon J H, Stehlé D. Fully homomophic encryption over the integers revisited[C]//Advances in Cryptology–EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, April 26-30, 2015, Proceedings, Part I. Berlin, Heidelberg: Springer Berlin Heidelberg, 2015: 513-536.
- Chillotti I, Gama N, Georgieva M, et al. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds[C]//Advances in Cryptology–ASIACRYPT 2016: 22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, December 4-8, 2016, Proceedings, Part I 22. Springer Berlin Heidelberg, 2016: 3-33.
- Chillotti I, Gama N, Georgieva M, et al. TFHE: fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34-91.
- TFHE:环面上全同态加密方案学习笔记
文章目录
- Real Torus
- Scale-Invariant LWE
- TLWE
- TGSW
- Operators
- Products
- Key Switching
- Simple Extraction
- Blind Rotate
- LHE & FHE
TFHE 是 FHEW 的改进,主要的优化思路是:使用 LWE 与 GSW 的"外积",取代 GSW 与 GSW 的“内积”,从而使得计算复杂度降低了一个多项式因子。
Real Torus
令 (R,+,×)(R,+,\times)(R,+,×) 是一个交换环,一个集合 MMM 叫做 RRR - (左) 模,如果 (M,+)(M,+)(M,+) 是一个阿贝尔群,并且存在一个bi-distributive(双分布?)、homogeneous(齐次)的 external operation (product),⋅:R×M→M\cdot: R \times M \to M⋅:R×M→M,即:对于任意的 r,s∈Rr,s \in Rr,s∈R 和 x,y∈Mx,y \in Mx,y∈M,都有,
- 1R⋅x=x1_R \cdot x = x1R⋅x=x
- (r+s)⋅x=r⋅x+s⋅x(r+s) \cdot x = r \cdot x+ s \cdot x(r+s)⋅x=r⋅x+s⋅x
- r⋅(x+y)=r⋅x+r⋅yr \cdot (x+y) = r \cdot x + r \cdot yr⋅(x+y)=r⋅x+r⋅y
- (r×s)⋅x=r⋅(s⋅x)(r \times s) \cdot x = r \cdot(s \cdot x)(r×s)⋅x=r⋅(s⋅x)
令 T:=R/Z\mathbb T := \mathbb R/\mathbb ZT:=R/Z 是集合 {r(mod1):r∈R}\{r \pmod 1: r \in \mathbb R\}{r(mod1):r∈R},这叫做实数环面(real Torus)。由于 mod 1 projection 与 real product 不兼容(例如,0T×0.5T0_\mathbb T \times 0.5_\mathbb T0T×0.5T 是未定义的,容易验证 0×0.5≠1×0.50 \times 0.5 \neq 1 \times 0.50×0.5=1×0.5),因此 Torus 不是 Ring。不过,容易发现 T\mathbb TT 是个 Z\mathbb ZZ-模(比如,0Z⋅0.5T=0T0_\mathbb Z \cdot 0.5_\mathbb T = 0_\mathbb T0Z⋅0.5T=0T 是 well define 的)。
简记 TN[X]:=R[X]/(XN+1,1)\mathbb T_N[X] := \mathbb R[X]/(X^N+1,1)TN[X]:=R[X]/(XN+1,1),ZN[X]:=Z[X]/(XN+1)\mathbb Z_N[X] := \mathbb Z[X]/(X^N+1)ZN[X]:=Z[X]/(XN+1),易知 (TN[X]k,+,⋅)(\mathbb T_N[X]^k,+,\cdot)(TN[X]k,+,⋅) 是一个 ZN[X]\mathbb Z_N[X]ZN[X]-模。
同时,如果 MMM 是个 RRR-模,那么它的向量或矩阵 Mn,m(M)\mathcal M_{n,m}(M)Mn,m(M) 也是 RRR-模。因此,Mn,m(T)\mathcal M_{n,m}(\mathbb T)Mn,m(T) 是 Z\mathbb ZZ-模,Mn,m(TN[X]k)\mathcal M_{n,m}(\mathbb T_N[X]^k)Mn,m(TN[X]k) 是 ZN[X]\mathbb Z_N[X]ZN[X]-模。
令 B:={0,1}⊂Z\mathbb B := \{0,1\} \subset \mathbb ZB:={0,1}⊂Z,简记 BN[X]:=B[X]/(XN+1)⊂ZN[X]\mathbb B_N[X] := \mathbb B[X]/(X^N+1) \subset \mathbb Z_N[X]BN[X]:=B[X]/(XN+1)⊂ZN[X]

一般来说, distributions over the torus do not have expectation nor variance(例如,均匀分布)。但是,如果分布 χ\chiχ 是集中的(concentrated,它的 support 包含在 T\mathbb TT 上的某个半径 14\dfrac{1}{4}41 的球内),那么还是可以定义期望和方差的:
- Var(χ):=minxˉ∈T∑χ∣x−xˉ∣2Var(\chi) := \min_{\bar x \in \mathbb T} \sum \chi|x-\bar x|^2Var(χ):=minxˉ∈T∑χ∣x−xˉ∣2
- E(χ):=argminxˉ∈T∑χ∣x−xˉ∣2E(\chi) := \arg\min_{\bar x \in \mathbb T} \sum \chi|x-\bar x|^2E(χ):=argminxˉ∈T∑χ∣x−xˉ∣2
我们说 Tn\mathbb T^nTn 或者 TN[X]k\mathbb T_N[X]^kTN[X]k 上的分布 χ′\chi'χ′ 是集中的,当今当它的每一个系数都是独立的集中的分布。类似于实数域上的性质,对于 e1,e2∈Ze_1,e_2 \in \mathbb Ze1,e2∈Z,集中分布的线性组合 χ=e1⋅χ1+e2⋅χ2\chi = e_1 \cdot \chi_1 + e_2 \cdot \chi_2χ=e1⋅χ1+e2⋅χ2,它也是集中的,并且
- E(χ)=e1⋅E(χ1)+e2⋅E(χ2)E(\chi) = e_1 \cdot E(\chi_1) + e_2 \cdot E(\chi_2)E(χ)=e1⋅E(χ1)+e2⋅E(χ2)
- Var(χ)≤e12⋅Var(χ1)+e22⋅Var(χ2)Var(\chi) \le e_1^2 \cdot Var(\chi_1) + e_2^2 \cdot Var(\chi_2)Var(χ)≤e12⋅Var(χ1)+e22⋅Var(χ2)
对于 Tk\mathbb T^kTk 上的向量 xxx,我们定义
∥x∥p:=minu∈x+Zk(∥u∥p)\|x\|_p := \min_{u \in x+\mathbb Z^k}(\|u\|_p) ∥x∥p:=u∈x+Zkmin(∥u∥p)
满足三角不等式,但它不是范数:Tk\mathbb T^kTk 不是向量空间,且 ∥⋅∥p\|\cdot\|_p∥⋅∥p 不是齐次的。不过 ∥⋅∥p\|\cdot\|_p∥⋅∥p 是 sub-homogeneous 的,∥m⋅x∥p≤∣m∣∥x∥p,∀m∈Z\|m \cdot x\|_p \le |m|\|x\|_p, \forall m \in \mathbb Z∥m⋅x∥p≤∣m∣∥x∥p,∀m∈Z。对于多项式 P∈TN[X]P \in \mathbb T_N[X]P∈TN[X],定义 ∥P∥p:=∥P⃗∥p\|P\|_p := \|\vec P\|_p∥P∥p:=∥P∥p,其中 P⃗∈[−0.5,0.5]N\vec P \in [-0.5,0.5]^{N}P∈[−0.5,0.5]N 是它的系数表示。
对于矩阵 A∈Mp,q(TN[X])A \in \mathcal M_{p,q}(\mathbb T_N[X])A∈Mp,q(TN[X]),我们定义
∥A∥∞:=maxi,j∥ai,j∥∞\|A\|_\infty := \max_{i,j} \|a_{i,j}\|_\infty ∥A∥∞:=i,jmax∥ai,j∥∞
Lipschitz function:我们说函数 f:Tm→Tnf:\mathbb T^m \to \mathbb T^nf:Tm→Tn 是 κ\kappaκ-Lipschitz 的,如果满足
∥f(x)−f(y)∥∞≤κ∥x−y∥∞,∀x,y\|f(x)-f(y)\|_\infty \le \kappa\|x-y\|_\infty, \forall x,y ∥f(x)−f(y)∥∞≤κ∥x−y∥∞,∀x,y
即任意两点间的连线斜率是“一致有界”的,上界 κ\kappaκ 叫做 Lipschitz 常数。
Scale-Invariant LWE
FHEW 采用了 Cheon 等人提出的 Scale-Invariant LWE 变体(回顾下 BFV 中的除以模数):令秘密 s∈Zns \in \mathbb Z^ns∈Zn,令 ξ\xiξ 是实数域 R\mathbb RR 上的错误分布,定义 LWEs,ξLWE_{s,\xi}LWEs,ξ 是 Tn×T\mathbb T^n \times \mathbb TTn×T 上的分布,样本形如 (a,b)(a,b)(a,b),其中 a∈Tna \in \mathbb T^na∈Tn 是均匀随机的,错误 e←ξe \leftarrow \xie←ξ,计算 b:=s⋅a+eb:=s \cdot a+eb:=s⋅a+e(先是环作用,然后是群加法)。类似一般的 LWE 问题,这个变体也分为 Search 和 Decision 两个版本。
我们称 phase(相位)是一个关于秘密 sss 的线性函数 ϕs:Tn×T→T\phi_s:\mathbb T^n \times \mathbb T \to \mathbb Tϕs:Tn×T→T,定义为 ϕs(a,b):=b−s⋅a\phi_s(a,b) := b-s \cdot aϕs(a,b):=b−s⋅a,容易看出 LWEs,ξLWE_{s,\xi}LWEs,ξ 就是 ϕs\phi_sϕs 的 kernel 的近似 ϕs(LWEs,ξ)=e≈0\phi_s(LWE_{s,\xi})=e \approx 0ϕs(LWEs,ξ)=e≈0
由于 ϕs(a,b)=μ\phi_s(a,b) = \muϕs(a,b)=μ 的一个 trivial preimage 是 (0n,μ)(0^n,\mu)(0n,μ),根据线性关系,
ϕs(LWEs,ξ+(0n,μ))=e+μ≈μ∈T\phi_s(LWE_{s,\xi}+(0^n,\mu)) = e+\mu \approx \mu \in \mathbb T ϕs(LWEs,ξ+(0n,μ))=e+μ≈μ∈T
因此,我们可以构造一个 symmetric-key variant Regev’s encryption scheme,定义明文空间为离散集合 M∈TM \in \mathbb TM∈T(例如 {0,0.5}\{0,0.5\}{0,0.5}),加密为 Encs(μ∈M):=LWEs,ξ+(0n,μ)Enc_s(\mu \in M) := LWE_{s,\xi}+(0^n,\mu)Encs(μ∈M):=LWEs,ξ+(0n,μ),解密为 Decs(c∈Tn+1):=round(ϕs(c),M)Dec_s(c \in \mathbb T^{n+1}) := round(\phi_s(c),M)Decs(c∈Tn+1):=round(ϕs(c),M)。只要 ξ\xiξ 的高斯参数 α=O(R/p)\alpha=O(R/\sqrt p)α=O(R/p)(对应的标准差为 σ=α2π\sigma=\alpha\sqrt{2\pi}σ=α2π),则解密正确的概率是压倒性的 1−2−p1-2^{-p}1−2−p,其中 RRR 是 MMM 的 packing radius。
如果想要得到 asymmetric variant 的方案,只需要将公钥 pkpkpk 定义为随机 LWEs,ξLWE_{s,\xi}LWEs,ξ 的样本列表,加密算法中的 LWEs,ξLWE_{s,\xi}LWEs,ξ 简单地修改为 small random subset sum ∑i∈Ipki\sum_{i \in I} pk_i∑i∈Ipki,而解密算法不变。
TLWE
TFHE 定义了一个抽象的 Scale-Invariant Generalization LWE over the Torus,它可以被实例化为多种问题:LWE、RLWE、MLWE 以及 Approx-GCD、NTRU。
Abstract TLWE problems:令 I⊆Z[X]I \subseteq \mathbb Z[X]I⊆Z[X] 是一个理想,定义 R:=Z[X]/I\mathfrak R:=\mathbb Z[X]/IR:=Z[X]/I,TI[X]:=T[X]/I\mathbb T_I[X] := \mathbb T[X]/ITI[X]:=T[X]/I,函数 phase 是一族 Lipschitz morphism(态射){ϕs:RM→TI[X]}S\{\phi_s:{}_\mathfrak R M \to \mathbb T_I[X]\}_S{ϕs:RM→TI[X]}S。我们说 general TLWE problem 是由 RM{}_\mathfrak R MRM 上的错误分布 ξ\xiξ、一族由秘密 sss 索引的态射 {ϕs}S\{\phi_s\}_S{ϕs}S 所指定的。我们定义 homogeneous TLWE distribution 为 Uker(ϕs)+ξ\mathcal U_{\ker(\phi_s)}+\xiUker(ϕs)+ξ,并可定义 Search 和 Decision 两个版本的问题。
- 如果设置 I=(X+1)I=(X+1)I=(X+1),那么 R=Z,TI[X]=T\mathfrak R = \mathbb Z, \mathbb T_I[X] = \mathbb TR=Z,TI[X]=T,
- 设置 M=Tn+1M=\mathbb T^{n+1}M=Tn+1 以及 ϕs(a,b)=b−s⋅a\phi_s(a,b)=b-s \cdot aϕs(a,b)=b−s⋅a,其中 S⊆ZnS\subseteq \mathbb Z^nS⊆Zn,那么这是 scale-invariant LWE
- 设置 M=Zqn+1M=\mathbb Z_q^{n+1}M=Zqn+1 以及 ϕs(a,b)=(b−s⋅a)/q\phi_s(a,b)=(b-s \cdot a)/qϕs(a,b)=(b−s⋅a)/q,其中 S⊆ZqnS\subseteq \mathbb Z_q^nS⊆Zqn,那么这是 LWE mod q
- 设置 M=TM=\mathbb TM=T 以及 ϕp(x)=p⋅x\phi_p(x)=p \cdot xϕp(x)=p⋅x,其中 S⊆ZS\subseteq \mathbb ZS⊆Z,那么这是 (dual) approx-GCD problem
- 如果设置 I=(XN+1)I=(X^N+1)I=(XN+1),那么 R=ZN[X],TI[X]=TN[X]\mathfrak R = \mathbb Z_N[X], \mathbb T_I[X] = \mathbb T_N[X]R=ZN[X],TI[X]=TN[X],
- 设置 M=TN[X]2M=\mathbb T_N[X]^{2}M=TN[X]2 以及 ϕs(a,b)=b−s⋅a\phi_s(a,b)=b-s \cdot aϕs(a,b)=b−s⋅a,其中 S⊆ZN[X]S\subseteq \mathbb Z_N[X]S⊆ZN[X],那么这是 Ring LWE
- 设置 M=TN[X]k×(k+1)M=\mathbb T_N[X]^{k \times (k+1)}M=TN[X]k×(k+1) 以及 ϕs(a,b)=b−s⋅a\phi_s(a,b)=b-s \cdot aϕs(a,b)=b−s⋅a,其中 S⊆ZN[X]kS\subseteq \mathbb Z_N[X]^kS⊆ZN[X]k,那么这是 Module LWE
- 设置 M=TN[X]2M=\mathbb T_N[X]^{2}M=TN[X]2 以及 ϕf,g(x,y)=fx−gy\phi_{f,g}(x,y)=fx-gyϕf,g(x,y)=fx−gy,其中 S⊆ZN[X]2S\subseteq \mathbb Z_N[X]^2S⊆ZN[X]2,那么这是 scale invariant NTRU
接下来,TFHE 定义了一个典范的 TLWE。
Canonical T®LWE problem:令 k≥1k \ge 1k≥1 是正整数,N∈Z+N\in \mathbb Z^+N∈Z+ 是 222 的幂次,α∈R≥0\alpha \in \mathbb R_{\ge 0}α∈R≥0 是标准差。密钥空间 S=BN[X]kS = \mathbb B_N[X]^kS=BN[X]k,其中的 sss 是 n≈kNn \approx kNn≈kN 比特均匀随机数。相位 ϕs\phi_sϕs 是定义在 M=TN[X]k×TN[X]M = \mathbb T_N[X]^k \times \mathbb T_N[X]M=TN[X]k×TN[X] 上的 nnn-Lipschitz 函数 ϕs(a,b)=b−s⋅a\phi_s(a,b) = b-s \cdot aϕs(a,b)=b−s⋅a,错误分布为 ξ=(0k,DTN[X],α)\xi=(0^k,D_{\mathbb T_N[X],\alpha})ξ=(0k,DTN[X],α),那么一个齐次 TLWE 样本就形如 (a,s⋅a+e)∈M(a,s \cdot a+e) \in M(a,s⋅a+e)∈M,其中的 mask 取自 a←UTN[X]ka \leftarrow \mathcal U_{\mathbb T_N[X]^k}a←UTN[X]k,error 取自 e←DTN[X],αe \leftarrow D_{\mathbb T_N[X],\alpha}e←DTN[X],α
-
我们说一个样本是 trivial 的,如果 a=0a=0a=0,此时的样本形如 (0k,e)(0^k,e)(0k,e)
-
我们说一个样本是 noiseless 的,如果 α=0\alpha=0α=0,此时的样本形如 (a,s⋅a)(a,s \cdot a)(a,s⋅a)
现在,Regev’s cryptosystem 可以被抽象为:
- 秘钥空间为 ϕs\phi_sϕs 的 index R:=Z[X]/I\mathfrak R :=\mathbb Z[X]/IR:=Z[X]/I
- 消息空间为 ϕs\phi_sϕs 的 image TI[X]:=T[X]/I\mathbb T_I[X] := \mathbb T[X]/ITI[X]:=T[X]/I
- 密文空间为 ϕs\phi_sϕs 的 domain RM{}_\mathfrak R MRM
- 消息 μ\muμ 的密文是 random preimage 的近似 Uϕs−1(μ)+ξ\mathcal U_{\phi_s^{-1}(\mu)}+\xiUϕs−1(μ)+ξ,对于 Canonical Form 来说就是 Uker(ϕs)+ξ+(0k,μ)\mathcal U_{\ker(\phi_s)}+\xi+(0^k,\mu)Uker(ϕs)+ξ+(0k,μ)
- 密文 ccc 的(近似的)明文是它的 image ϕs(c)\phi_s(c)ϕs(c)
由于上述方案的解密结果是带噪的,适合于浮点数计算或者差分隐私(differential privacy)。如果需要精确值,有两种选择:
- 第一种,限制消息空间为 discrete subset,并使得 packing radius 大于 ξ\xiξ 的振幅,从而可以使用园整运算获得精确值。但是,这使得非线性运算的正确性分析较为复杂,并且离散后的阿贝尔群的空间太小了。
- 第二种,限制噪声期望为 E(ξ)=0E(\xi)=0E(ξ)=0,从而明文就是期望值 E(ϕs(c))E(\phi_s(c))E(ϕs(c))。这使得噪声分析变得简单,同时可以支持无限精度的连续明文空间。
TFHE 使用第一种方案来评估 worst case 的噪声,使用第二种方案来评估 average case 的噪声。首先需要定义一个概率空间 Ω\OmegaΩ,并将 TLWE 样本视为一个随机分布,而非某个数值。我们说 c∈TN[X]k+1c \in \mathbb T_N[X]^{k+1}c∈TN[X]k+1 是一个 valid TLWE sample,当仅当 ϕs(c)\phi_s(c)ϕs(c) 在 Ω\OmegaΩ 上是集中分布的。接下来定义,
- 消息 msg(c):=E(ϕs(c))msg(c):=E(\phi_s(c))msg(c):=E(ϕs(c))
- 噪声 Err(c):=ϕs(c)−msg(c)Err(c):=\phi_s(c)-msg(c)Err(c):=ϕs(c)−msg(c)
- 方差 Var(Err(c)):=Var(ϕs(c))Var(Err(c)):=Var(\phi_s(c))Var(Err(c)):=Var(ϕs(c))
- 振幅 ∥Err(c)∥∞\|Err(c)\|_\infty∥Err(c)∥∞ 定义为满足 Pr[Err(c)≥B]=negl(λ)Pr[Err(c) \ge B] = negl(\lambda)Pr[Err(c)≥B]=negl(λ) 的最大振幅(maximum amplitude)
根据相位的线性关系,对应组合系数 ei∈Re_i \in \mathfrak Rei∈R,密文 c=∑Iei⋅cic = \sum_I e_i \cdot c_ic=∑Iei⋅ci 满足以下关系:
- msg(c)=∑Iei⋅msg(ci)msg(c) = \sum_I e_i \cdot msg(c_i)msg(c)=∑Iei⋅msg(ci),
- Var(Err(c))≤∑I∥ei∥22⋅Var(Err(ci))Var(Err(c)) \le \sum_I \|e_i\|_2^2 \cdot Var(Err(c_i))Var(Err(c))≤∑I∥ei∥22⋅Var(Err(ci))
- ∥Err(c)∥∞≤∑I∥ei∥1⋅∥Err(ci)∥∞\|Err(c)\|_\infty \le \sum_I \|e_i\|_1 \cdot \|Err(c_i)\|_\infty∥Err(c)∥∞≤∑I∥ei∥1⋅∥Err(ci)∥∞
TGSW
由于 LWE 密文适合线性运算,但对于非线性运算似乎少了些属性(when it comes to non linear operations on the samples, TLWE seems to miss some properties)。最知名的两种解决方案是:BGV constructions 和 GSW constructions,TFHE 关注 GSW 的一个 Torus 上的 generalized scale invariant version 的变体。
为了控制噪声增长,TFHE 给出了一个 approximate decomposition(实数的有限精度的近似分解)。首先给出一个抽象概念,之后再给出一个典范。
Abstract Gadget Decomposition:令 MMM 是一个 R\mathfrak RR-模,分解算法是一个有效的算法 DecH,β,ϵ(v)Dec_{H,\beta,\epsilon}(v)DecH,β,ϵ(v),其中 H∈Ml′H \in M^{l'}H∈Ml′ 是 gadget,β∈R>0\beta \in \mathbb R_{>0}β∈R>0 是 quality,ϵ∈R>0\epsilon \in \mathbb R_{>0}ϵ∈R>0 是 precision,它将任意的 TLWE 样本 v∈Mv \in Mv∈M 分解为一个(随机的) small 向量 u∈Rl′u \in \mathfrak R^{l'}u∈Rl′,使得 ∥u∥∞≤β\|u\|_\infty \le \beta∥u∥∞≤β 以及 ∥u⋅H−v∥∞≤ϵ\|u\cdot H-v\|_\infty \le \epsilon∥u⋅H−v∥∞≤ϵ,并且期望 Ev(u⋅H−v)=0E_v(u\cdot H-v)=0Ev(u⋅H−v)=0
分解算法本应是随机的,但是根据 Independence Heuristic,可以近似地认为各个系数服从独立随机的集中分布,因此也可以直接使用确定性的算法。
Canonical Gadget Decomposition:对于 Canonical TLWE 样本,我们设置 M=TN[X]k+1M = \mathbb T_N[X]^{k+1}M=TN[X]k+1,令 l,Bgl,B_gl,Bg 是正整数,并设置 l′=(k+1)ll'=(k+1)ll′=(k+1)l,那么 Gadget H∈Ml′=Ml′,k+1(TN[X])H \in M^{l'}=\mathcal M_{l',k+1}(\mathbb T_N[X])H∈Ml′=Ml′,k+1(TN[X]) 定义为
H=[Bg−10⋯00Bg−2⋯0⋮⋮⋮Bg−l0⋯00⋮⋱⋮00⋯0Bg−10⋯Bg−2⋮⋮⋮00⋯0Bg−l]∈M(k+1)lH = \left[\begin{array}{c|ccc|c} B_g^{-1} & 0 & \cdots & 0 & 0\\ B_g^{-2} && \cdots && 0\\ \vdots && \vdots && \vdots\\ B_g^{-l} & 0 & \cdots & 0 & 0\\ \hline \vdots && \ddots && \vdots\\ \hline 0 & 0 & \cdots & 0 & B_g^{-1}\\ 0 && \cdots && B_g^{-2}\\ \vdots && \vdots && \vdots\\ 0 & 0 & \cdots & 0 & B_g^{-l}\\ \end{array}\right] \in M^{(k+1)l} H=Bg−1Bg−2⋮Bg−l⋮00⋮00000⋯⋯⋮⋯⋱⋯⋯⋮⋯000000⋮0⋮Bg−1Bg−2⋮Bg−l∈M(k+1)l
它包含 l′=(k+1)ll'=(k+1)ll′=(k+1)l 个 RM{}_\mathfrak R MRM 中的元素,乘以系数 u∈Rl′u \in \mathfrak R^{l'}u∈Rl′ 后将组合出一个 RM{}_\mathfrak R MRM 中的元素 vvv,并且 β=Bg/2\beta=B_g/2β=Bg/2,ϵ=Bg−l/2\epsilon=B_g^{-l}/2ϵ=Bg−l/2(就是 BgB_gBg 进制的浮点小数的有限精度表示)
近似分解算法 DecH,β,ϵ:M→Rl′Dec_{H,\beta,\epsilon}:M \to \mathfrak R^{l'}DecH,β,ϵ:M→Rl′ 定义如下:

接下来,我们定义 TGSW 样本。首先是抽象描述,接下来是典范描述。
Abstract TGSW samples:回顾 Abstract TLWE samples 中的 ξ,ϕs,RM\xi,\phi_s,{}_\mathfrak R Mξ,ϕs,RM,以及 H∈Ml′H \in M^{l'}H∈Ml′ 对应的 DecH,β,ϵDec_{H,\beta,\epsilon}DecH,β,ϵ,我们说 C∈Ml′C \in M^{l'}C∈Ml′ 是一个关于 μ∈R\mu \in \mathfrak Rμ∈R 的fresh TGSW sample,当仅当 C=Z+μ⋅HC=Z+\mu \cdot HC=Z+μ⋅H,其中 Z∈Ml′Z\in M^{l'}Z∈Ml′ 的每个 element 都是一个关于 s∈BN[X]ks \in \mathbb B_N[X]^ks∈BN[X]k 的齐次 TLWE 样本。我们说 CCC 是一个 valid TGSW sample,当仅当存在一个 μ∈R\mu \in \mathfrak Rμ∈R 使得 C−μ⋅HC-\mu \cdot HC−μ⋅H 的每个 element 都是 valid TLWE sample。另外,我们将 TLWE 的相位扩展为 ϕs(C)∈TI[X]l′\phi_s(C) \in \mathbb T_I[X]^{l'}ϕs(C)∈TI[X]l′,它的每个分量就是对 CCC 的各个 element 分别计算相位。
Canonical T®GSW samples:回顾 Canonical TLWE samples 以及 Canonical Gadget Decomposition 中的各个参数的设置,秘密 s∈BN[X]ks \in \mathbb B_N[X]^ks∈BN[X]k,那么对应的 T®GSW 样本为 C∈Ml′=M(k+1)l,k+1(TN[X])C \in M^{l'} = \mathcal M_{(k+1)l,k+1}(\mathbb T_N[X])C∈Ml′=M(k+1)l,k+1(TN[X]),它包含 (k+1)l(k+1)l(k+1)l 行,且 C−μ⋅HC-\mu \cdot HC−μ⋅H 的每一行都是 TN[X]k+1\mathbb T_N[X]^{k+1}TN[X]k+1 上的齐次 T®LWE 样本。
根据 phase 的线性,对于组合系数 ei∈Re_i \in \mathfrak Rei∈R,C=∑Iei⋅CiC = \sum_I e_i \cdot C_iC=∑Iei⋅Ci 是 μ=∑Iei⋅μi\mu = \sum_I e_i \cdot \mu_iμ=∑Iei⋅μi 的密文,并且
Var(C)≤∑I∥ei∥22⋅Var(Ci)∥Err(C)∥∞≤∑I∥ei∥1⋅∥Err(Ci)∥∞\begin{aligned} Var(C) &\le \sum_I \|e_i\|_2^2 \cdot Var(C_i)\\ \|Err(C)\|_\infty &\le \sum_I \|e_i\|_1 \cdot \|Err(C_i)\|_\infty \end{aligned} Var(C)∥Err(C)∥∞≤I∑∥ei∥22⋅Var(Ci)≤I∑∥ei∥1⋅∥Err(Ci)∥∞
另外,如果 sss 是二元系数的,那么任意的 A∈Mp,k+1(TN[X])A \in \mathcal M_{p,k+1}(\mathbb T_N[X])A∈Mp,k+1(TN[X]),都有
∥ϕs(A)∥∞≤(1+kN)∥A∥∞\|\phi_s(A)\|_\infty \le (1+kN)\|A\|_\infty ∥ϕs(A)∥∞≤(1+kN)∥A∥∞
也就是说,Canonical TGSW samples 中定义的 ϕs\phi_sϕs 是一族 (1−kN)(1-kN)(1−kN)-Lipschitz 函数。
Operators
Products
TFHE 观察到,GSW 的不对称性有两个方面,
- 如 AP14 所描述的噪声增长的不对称性,这可以支持长链乘法。
- 解密操作的不对称性,即大部分运算是不必要的,只有所谓 “big coefficient” 对应的那一个 LWE 样本被用于解密出明文。
External product:我们定义(右结合)算符 ⊡\boxdot⊡ 为
⊡:TGSW×TLWE→TLWE(A∈RMl′,b∈RM)↦DecH,β,ϵ(b)⋅A∈RM\begin{aligned} \boxdot: TGSW \times TLWE &\to TLWE\\ (A \in {}_\mathfrak R M^{l'},b \in {}_\mathfrak R M) &\mapsto Dec_{H,\beta,\epsilon}(b) \cdot A \in {}_\mathfrak R M \end{aligned} ⊡:TGSW×TLWE(A∈RMl′,b∈RM)→TLWE↦DecH,β,ϵ(b)⋅A∈RM
容易验证它是 μA⋅μb\mu_A \cdot \mu_bμA⋅μb 的密文。噪声分析如下,


而 GSW 的“内积”可以被视为多个“外积”组成的向量。
Internal Product:我们定义(右结合)算符 ⊠\boxtimes⊠ 为
⊠:TGSW×TGSW→TGSW(A∈RMl′,B∈RMl′)↦[A⊡b1A⊡b2⋮A⊡bl′]∈RMl′\begin{aligned} \boxtimes: TGSW \times TGSW &\to TGSW\\ (A \in {}_\mathfrak R M^{l'},B \in {}_\mathfrak R M^{l'}) &\mapsto \begin{bmatrix} A \boxdot b_1\\ A \boxdot b_2\\ \vdots\\ A \boxdot b_{l'}\\ \end{bmatrix} \in {}_\mathfrak R M^{l'} \end{aligned} ⊠:TGSW×TGSW(A∈RMl′,B∈RMl′)→TGSW↦A⊡b1A⊡b2⋮A⊡bl′∈RMl′
容易验证它是 μA⋅μB\mu_A \cdot \mu_BμA⋅μB 的密文,噪声分析与 External product 基本一致。
Key Switching
TFHE 扩展了秘钥切换的概念,定义了 TLWE 上的关于 RRR-Lipschitz 的线性态射 f:ZTp→TN[X]f:{}_\mathbb Z \mathbb T^p \to \mathbb T_N[X]f:ZTp→TN[X] 的秘钥切换。假设从 K∈Bn\mathfrak K \in \mathbb B^nK∈Bn 下的密文 c\mathfrak cc,切换到 K∈BN[X]kK \in \mathbb B_N[X]^kK∈BN[X]k 下的密文 ccc。
对于公开的态射 fff,秘钥切换的例程为 PubKS(f,KS,c)PubKS(f,KS,\mathfrak c)PubKS(f,KS,c),如图:

它的输出为 c∈T(R)LWEK(f(μ1,⋯,μp))c \in T(R)LWE_K(f(\mu_1,\cdots,\mu_p))c∈T(R)LWEK(f(μ1,⋯,μp)),噪声分析为

对于秘密的态射 fff,方便起见使用增广形式的私钥(第 n+1n+1n+1 分量置为 −1-1−1),此时 ϕK(c)=−K⋅c\phi_\mathfrak K(\mathfrak c) = -\mathfrak K \cdot \mathfrak cϕK(c)=−K⋅c。秘钥切换的例程为 PrivKS(KS(f),c)PrivKS(KS^{(f)},\mathfrak c)PrivKS(KS(f),c),如图:

它的输出为 c∈T(R)LWEK(f(μ1,⋯,μp))c \in T(R)LWE_K(f(\mu_1,\cdots,\mu_p))c∈T(R)LWEK(f(μ1,⋯,μp)),噪声分析为

Simple Extraction
由于 T®LWE 或 T®GSW 的消息空间是 TN[X]\mathbb T_N[X]TN[X],因此它包含 NNN 个环面 T\mathbb TT 上的槽(slot)。
对于 n=kNn=kNn=kN,LWE 的秘钥 K∈Bn\mathfrak K \in \mathbb B^nK∈Bn 和 RLWE 的秘钥 K∈BN[X]kK \in \mathbb B_N[X]^kK∈BN[X]k 可以相互转化(对应于同样的 nnn 长二元向量表示),并且 RLWE 的密文可以被视作是:LWE 密文的第一分量不断反循环移位,从而获得一系列的 LWE 密文的第二分量(仔细想一下 TN[X]\mathbb T_N[X]TN[X] 被 ZN[X]\mathbb Z_N[X]ZN[X] 环作用,其中理想为 I=(XN+1)I=(X^N+1)I=(XN+1))
给定 RLWE 样本 c=(a,b)∈RLWEK(μ)c=(a,b) \in RLWE_K(\mu)c=(a,b)∈RLWEK(μ) 以及位置 p∈[N]p \in [N]p∈[N],我们定义 SimpleExtractp(c)SimpleExtract_p(c)SimpleExtractp(c) 的输出是一个 LWE 样本 c=(a,b)∈LWEK(μp)\mathfrak c=(\mathfrak a,\mathfrak b) \in LWE_\mathfrak K(\mu_p)c=(a,b)∈LWEK(μp),
aN(i−1)+j:=ai[p−j],i∈[k]b:=bp\begin{aligned} \mathfrak a_{N(i-1)+j} &:= a_i[p-j], i \in [k]\\ \mathfrak b &:= b_p \end{aligned} aN(i−1)+jb:=ai[p−j],i∈[k]:=bp
其中 ai∈TN[X]a_i \in \mathbb T_N[X]ai∈TN[X] 使用 NNN-antiperiodic indexes 的系数向量表示,即 ai[j]a_i[j]ai[j] 是 XN−jX^{N-j}XN−j 的系数。
Blind Rotate
有时候旋转一个多项式(乘以 XiX^iXi)是有必要的。如果旋转程度被 LWE 加密 (a,b)∈Zp+1(a,b) \in \mathbb Z^{p+1}(a,b)∈Zp+1,多项式被 RLWE 加密 c∈TN[X]c \in \mathbb T_N[X]c∈TN[X],盲旋转的算法如下:

其输出为 ACC∈TRLWEK(X⟨s,a⟩−b⋅v)ACC \in TRLWE_K(X^{\langle s,a \rangle-b} \cdot v)ACC∈TRLWEK(X⟨s,a⟩−b⋅v),噪声分析为

LHE & FHE
TFHE 先提出了一个 LHE 的自动机模型:布尔门电路,使用 TGSW 密文作为控制线,使用 TLWE 密文作为数据线。然后使用“外积”来计算 Bootstrapping,这比使用“内积”的 FHEW 快一个小多项式因子。

还有 随机函数查找表、水平打包、垂直打包 等等技术。
作者没细看,略啦 (づ。◕ᴗᴗ◕。)づ
相关文章:

全同态加密:TFHE
参考文献: Cheon J H, Stehl D. Fully homomophic encryption over the integers revisited[C]//Advances in Cryptology–EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, …...

【计算机二级】综合题目
计算机二级python真题 文章目录计算机二级python真题一、《大学慕课 两问 》二、综合应用题——价值链三、基本操作题 ——信息输出一、《大学慕课 两问 》 附件中的文件data.txt 是教育部爱课程网中国大学MOOC平台的某个 HTML页面源文件,里面包含了我国参与MOOC建设的一批大学…...
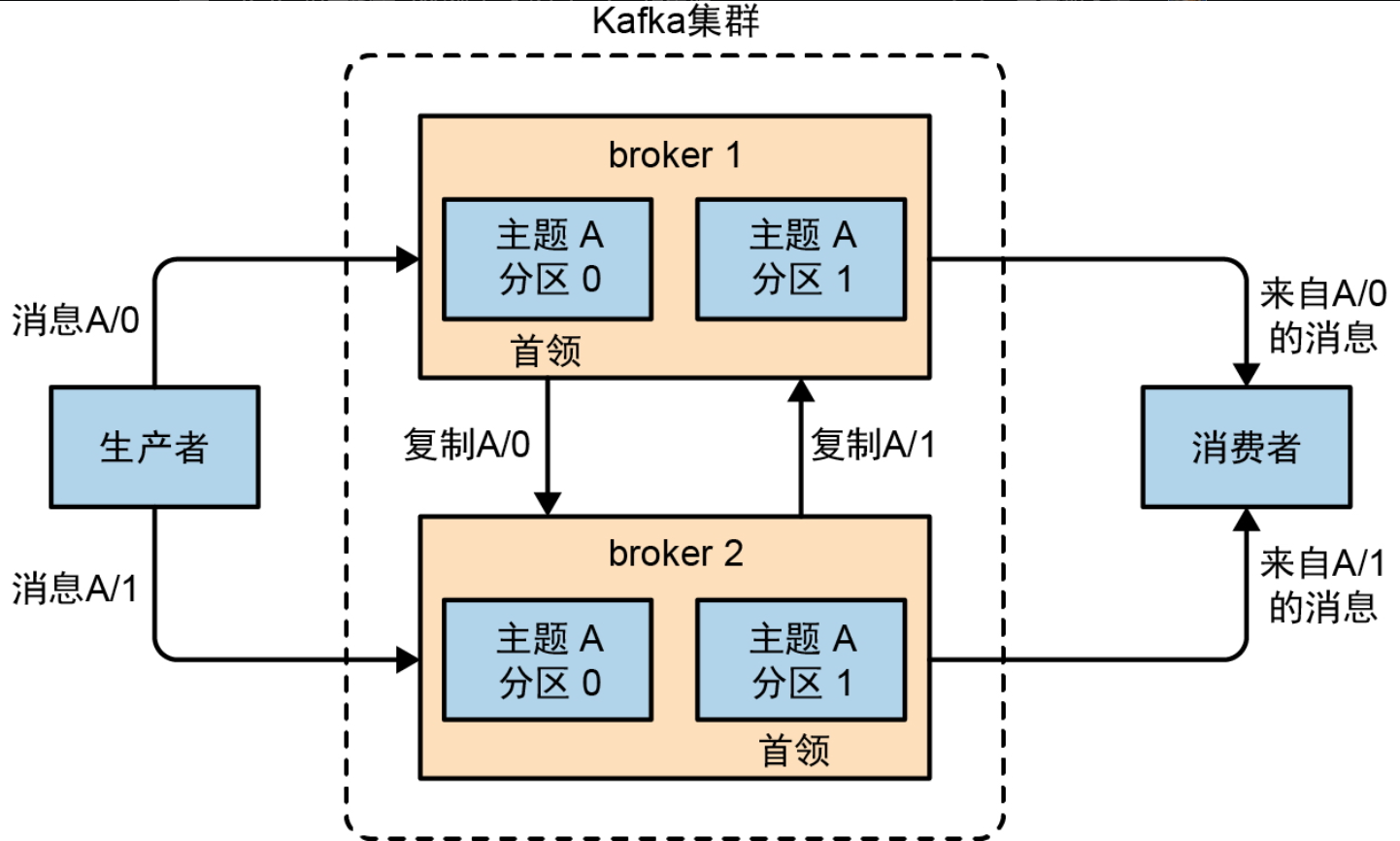
初识Kafka
介绍 Kafka Kafka 是一款基于发布与订阅的消息系统。 用生产者客户端 API 向 Kafka 生产消息,用消费者客户端 API 从 Kafka 读取这些消息。 Kafka 使用 Zookeeper 保存元数据信息。 Kafka 0.9 版本之前,除了 broker 之外, 消费者也会使用…...

【JavaEE】线程的状态
哈喽,大家好~我是保护小周ღ,本期为大家带来的是 Java 多线程的 线程的状态,New 新建状态,Runnable 运行状态,Blocked 阻塞状态,waiting 等待状态,Time_Waiting 超时等待状态,Termin…...
7个最受瞩目的 Python 库,提升你的开发效率
当今时代,数据分析和处理已经成为了各行各业中不可或缺的一环。Python作为一种非常流行的编程语言,为我们提供了许多强大的工具和库来处理不同类型的数据。 在这篇文章中,我将向您介绍七个非常有用的Python库,这些库各自有着独特…...
这些IT行业趋势,将改变2023
上一周,你被"AI"刷屏了吗? 打开任何一家科技媒体,人工智能都是不变的热门话题。周初大家还在用ChatGPT写论文、查资料、写代码,到周末的时候大家已经开始用GPT-4图像识别来做饭、Microsoft 365 Copilot 来写PPT了。 GP…...
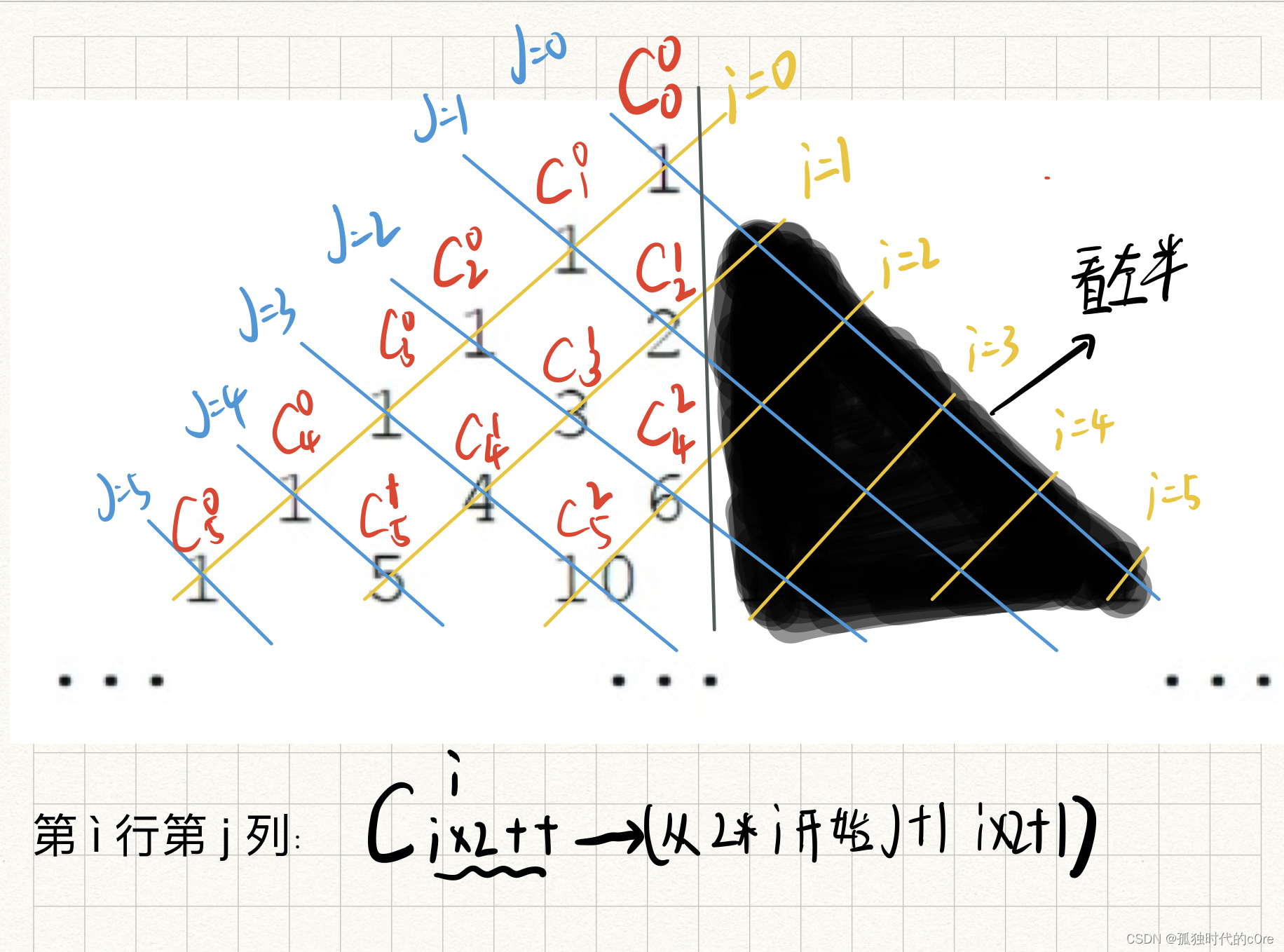
蓝桥杯每日一真题——[蓝桥杯 2021 省 B] 杨辉三角形(二分+规律)
文章目录[蓝桥杯 2021 省 B] 杨辉三角形题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路:全部代码:[蓝桥杯 2021 省 B] 杨辉三角形 题目描述 下面的图形是著名的杨辉三角形: 如果我们按从上到下、从左到右的顺序把所有数排成一列&…...
<C++> 类和对象(下)
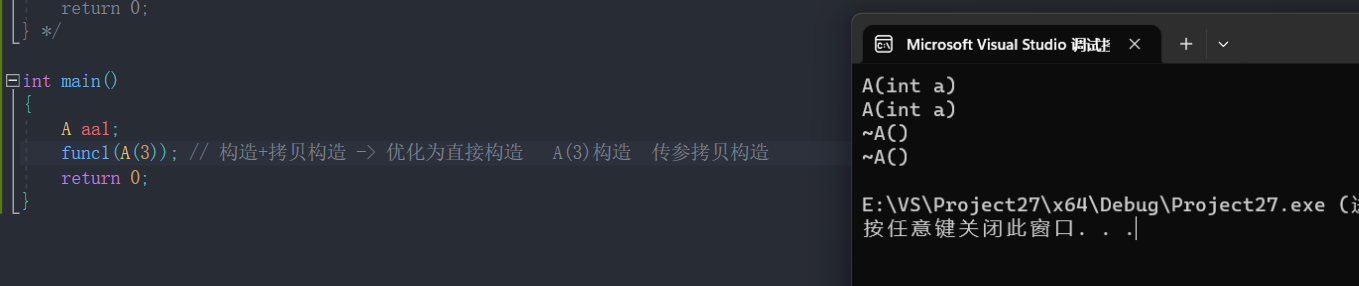
1.const成员函数将const修饰的“成员函数”称之为const成员函数,const修饰类成员函数,实际修饰该成员函数隐含的this指针,表明在该成员函数中不能对类的任何成员进行修改。class A { public:void Print() //这里隐藏了A* this指针{cout <…...
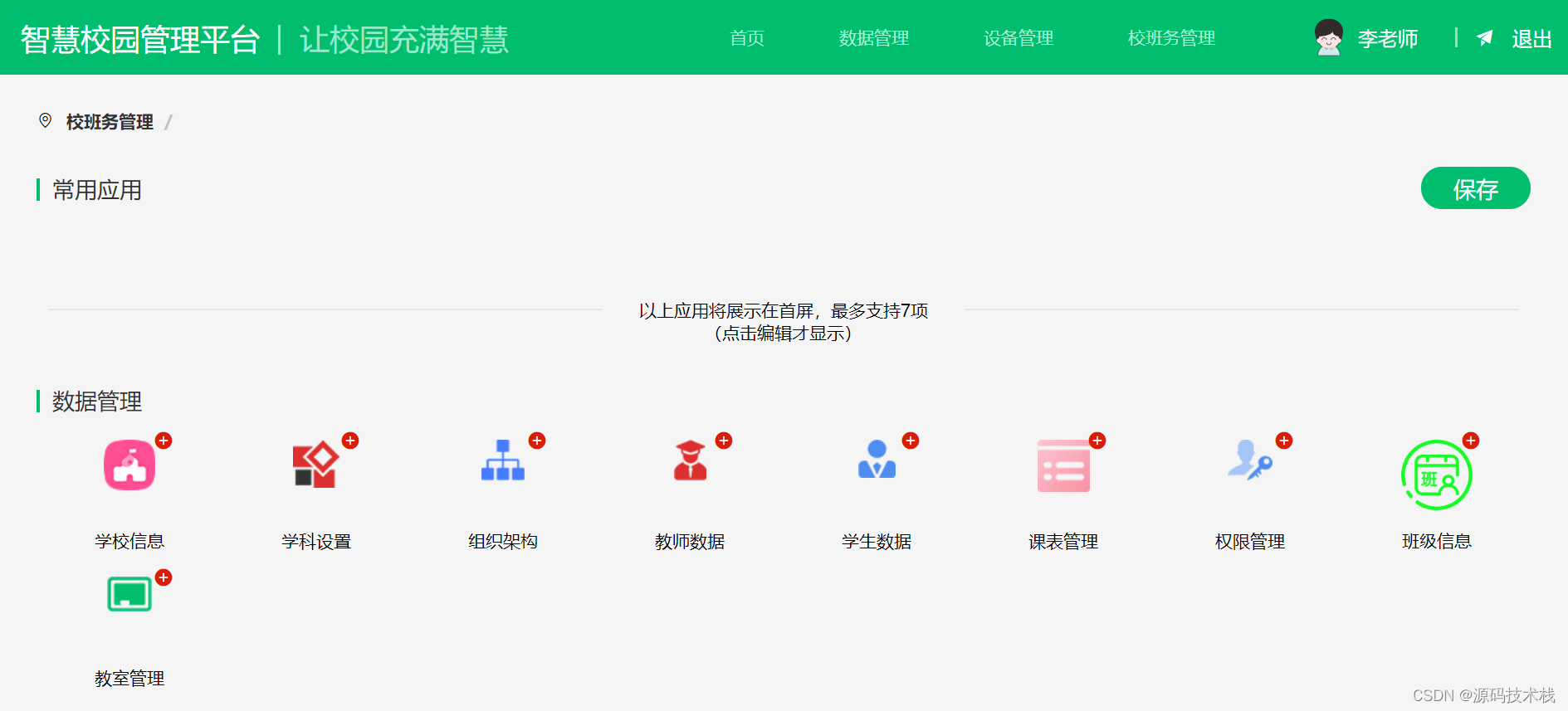
基于Springboot+Vue2前后端分离框架的智慧校园系统源码,智慧学校源码+微信小程序+人脸电子班牌
▶ 智慧校园开发环境: 1、使用springboot框架Javavue2 2、数据库MySQL5.7 3、移动端小程序使用小程序原生语音开发 4、电子班牌固件安卓7.1;使用Java Android原生 5、elmentui ,Quartz,jpa,jwt 智慧校园结构导图▶ 这…...

JavaEE-线程安全问题
1.线程安全的概念 如果多线程环境下代码运行的结果是符合我们预期的,即在单线程环境应该的结果,则说这个程序是线 程安全的. 为啥会出现线程安全问题? 本质原因: 线程在系统中的调度是无序的/随机的 (抢占式执行). 2.开始说明 先看个线程不安全的例子…...
【Node.js】身份认证,Cookie和Session的认证机制,express中使用session认证和JWT认证
Node.jsWeb开发模式如何选择Web开发模式身份认证什么是身份认证为什么要身份认证不同开发模式的身份认证Session认证机制提高身份认证的安全性Session的工作原理Express中使用Session认证Session认证机制的局限性JWT认证机制JWT的工作原理JWT的组成部分Express中使用JWT在登录成…...

Redis删除策略和淘汰策略
一、删除策略 删除策略就是针对已过期数据的处理策略。 针对过期数据要进行删除的时候都有哪些删除策略呢? 1.定时删除2.惰性删除3.定期删除1、立即删除 当key设置有过期时间,且过期时间到达时,由定时器任务立即执行对键的删除操作。 优…...

LFM雷达实现及USRP验证【章节2:LFM雷达测距】
目录 1. 参数设计 几个重要的约束关系 仿真参数设计 2. matlab雷达测距代码 完整源码 代码分析 回顾:LFM的基本原理请详见第一章 本章节将介绍LFM雷达测距的原理及实现 1. 参数设计 几个重要的约束关系 带通采样定理: 因此如果我们B80MHz时&a…...

菜鸟刷题Day5
⭐作者:别动我的饭 ⭐专栏:菜鸟刷题 ⭐标语:悟已往之不谏,知来者之可追 一.一维数组的动态和:1480. 一维数组的动态和 - 力扣(LeetCode) 描述 给你一个数组 nums 。数组「动态和」的计算公式…...
已解决AttributeError:module tensorflow no attribute app异常的正确解决方法,亲测有效!!!
已解决AttributeError:module tensorflow no attribute app异常的正确解决方法,亲测有效!!! 文章目录报错问题解决方法福利报错问题 粉丝群里面的一个小伙伴敲代码时发生了报错(当时他心里瞬间凉了一大截&…...
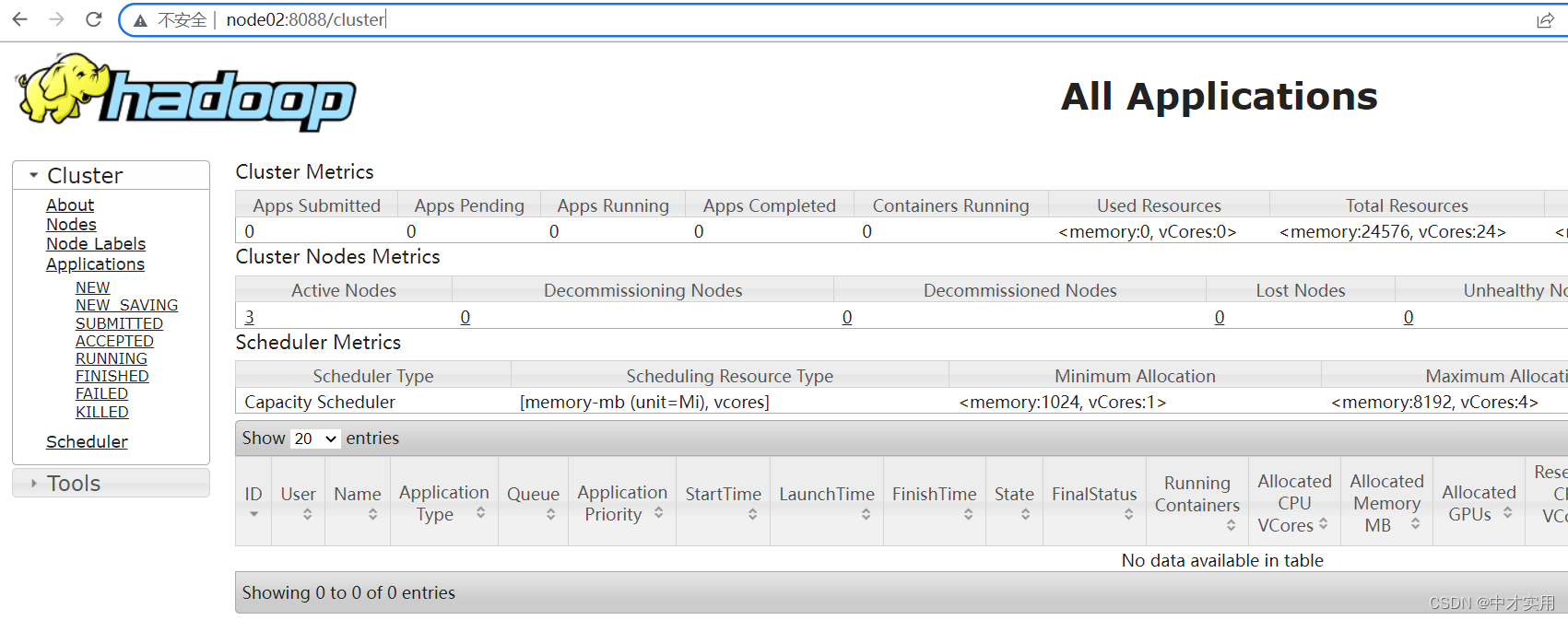
Hadoop集群环境配置搭建
一、简单介绍 Hadoop最早诞生于Cutting于1998年左右开发的一个全文文本搜索引擎 Lucene,这个搜索引擎在2001年成为Apache基金会的一个子项目,也是 ElasticSearch等重要搜索引擎的底层基础。 项目官方:https://hadoop.apache.org/ 二、Linux环…...

Thread类的基本用法
Thread类的基本用法🔎1.线程创建🌻继承Thread类🌼继承Thread重写run()方法🌼继承Thread匿名内部类🌻实现Runnable接口🌼实现Runnable接口重写run()方法🌼实现Runnable接口匿名内部类ἳ…...

YOLOV8改进:如何增加注意力模块?(以CBAM模块为例)
YOLOV8改进:如何增加注意力模块?(以CBAM模块为例)前言YOLOV8nn文件夹modules.pytask.pymodels文件夹总结前言 因为毕设用到了YOLO,鉴于最近V8刚出,因此考虑将注意力机制加入到v8中。 YOLOV8 代码地址&am…...

Spark Streaming DStream的操作
一、DStream的定义 DStream是离散流,Spark Streaming提供的一种高级抽象,代表了一个持续不断的数据流。DStream可以通过输入数据源来创建,比如Kafka、Flume,也可以通过对其他DStream应用高阶函数来创建,比如map、redu…...

蓝桥杯冲刺 - week1
文章目录💬前言🌲day192. 递归实现指数型枚举843. n-皇后问题🌲day2日志统计1209. 带分数🌲day3844. 走迷宫1101. 献给阿尔吉侬的花束🌲day41113. 红与黑🌲day51236. 递增三元组🌲day63491. 完全…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
