蓝桥杯冲刺 - week1
文章目录
- 💬前言
- 🌲day1
- 92. 递归实现指数型枚举
- 843. n-皇后问题
- 🌲day2
- 日志统计
- 1209. 带分数
- 🌲day3
- 844. 走迷宫
- 1101. 献给阿尔吉侬的花束
- 🌲day4
- 1113. 红与黑
- 🌲day5
- 1236. 递增三元组
- 🌲day6
- 3491. 完全平方数[简单数论]
- 🌲day7
- 466. 回文日期
💬前言
🚩第一周从最高频-分数占比最高开始练习!涉及算法标签[⚽️DFS,⚽️BFS,⚽️日期问题,⚽️哈希统计]
DFS乃是暴力搜索的基础,BFS常用于解决迷宫问题,日期问题可以视为常规题
⏳最后三个星期大家一起冲刺,祝大家rp++🏅
如果对您有帮助的话还请动动小手 点赞👍,收藏⭐️,关注❤️
🌲day1
92. 递归实现指数型枚举
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1≤n≤15
输入样例:
3
输出样例:
3
2
2 3
1
1 3
1 2
1 2 3
[按选取个数的枚举所有情况]- 选0~n个
#include<iostream>using namespace std;const int N = 20;
int n;
bool st[N];
int q[N];void dfs(int u, int start, int m) //当前位置u start开始选择升序填数 填满m个数结束分支
{if(u == m){for(int i = 0; i < m; i++) printf("%d ", q[i]);puts("");}for(int i = start; i <= n; i++){if(!st[u]){q[u] = i;st[u] = true;dfs(u + 1, i + 1, m);st[u] = false;}}
}int main()
{scanf("%d", &n);for (int i = 0; i <= n; i ++ ) //填满任意个数 - 枚举位数dfs(0, 1, i); return 0;
}
算法:枚举到第u位:前面每一位选或不选
三种状态st[] = 0,未枚举此位; st[] = 1此位选, st[] = 2此位不选
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 16;int n;
int st[N]; // 状态,记录每个位置当前的状态:0表示还没考虑,1表示选它,2表示不选它void dfs(int u)
{if (u > n){for (int i = 1; i <= n; i ++ )if (st[i] == 1)printf("%d ", i);puts("");return; //必须return【当做好习惯】}st[u] = 2;dfs(u + 1); // 第一个分支:不选st[u] = 0; // 恢复现场st[u] = 1;dfs(u + 1); // 第二个分支:选st[u] = 0;
}int main()
{cin >> n;dfs(1);return 0;
}
843. n-皇后问题
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..
正对角线: y = -x + b 与 副对角线:y = x + b (b为截距:枚举)
判断截距b是否被选择:
正对角线 b == x + y == u + i
副对角线:b == (-x + y) % n 【映射[0,n-1]】 == -u + i + n : [注意:加n为了防止负数超出数组范围]**
按行枚举 - u当前行
#include <iostream>using namespace std;const int N = 20;int n;//棋盘大小-n皇后
char g[N][N];//棋盘
bool col[N], dg[N], udg[N];//列 + 正对角线 + 反对角线void dfs(int u) // u为x
{if (u == n){for (int i = 0; i < n; i ++ ) puts(g[i]);//简用puts(输出一行 + 换行)puts("");return;}for (int i = 0; i < n; i ++ )//按行枚举 [u行][i列] : u为x, i为yif (!col[i] && !dg[u + i] && !udg[n - u + i]) //列标记 + 对角线截距标记{g[u][i] = 'Q';//()col[i] = dg[u + i] = udg[n - u + i] = true;dfs(u + 1);col[i] = dg[u + i] = udg[n - u + i] = false;g[u][i] = '.';}
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )g[i][j] = '.';dfs(0);return 0;
}
第二种搜索顺序
#include <iostream>using namespace std;const int N = 10;int n;
bool row[N], col[N], dg[N * 2], udg[N * 2]; //注意行列都要边标记
char g[N][N];void dfs(int x, int y, int s) //s统计已放皇后个数
{if (s > n) return;if (y == n) y = 0, x ++ ; //每行:按列搜索 (每行搜索完需换到下一行)if (x == n) //说明搜索到了终点(上一个y换行前(x, y)为(n - 1, n - 1):已经遍历完){if (s == n) //如果放入个数为n, 说明成功,输出答案{for (int i = 0; i < n; i ++ ) puts(g[i]);puts("");}return;}g[x][y] = '.';dfs(x, y + 1, s); if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]){row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;g[x][y] = 'Q';dfs(x, y + 1, s + 1); //每行:按列遍历g[x][y] = '.';row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;}
}int main()
{scanf("%d", &n);dfs(0, 0, 0);return 0;
}
🌲day2
日志统计
小明维护着一个程序员论坛。现在他收集了一份”点赞”日志,日志共有 N 行。
其中每一行的格式是:
ts id
表示在 ts 时刻编号 id 的帖子收到一个”赞”。
现在小明想统计有哪些帖子曾经是”热帖”。
如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞,小明就认为这个帖子曾是”热帖”。
具体来说,如果存在某个时刻 T 满足该帖在 [T,T+D) 这段时间内(注意是左闭右开区间)收到不少于 K 个赞,该帖就曾是”热帖”。
给定日志,请你帮助小明统计出所有曾是”热帖”的帖子编号。
输入格式
第一行包含三个整数 N,D,K。
以下 N 行每行一条日志,包含两个整数 ts 和 id。
输出格式
按从小到大的顺序输出热帖 id。
每个 id 占一行。
数据范围
1≤K≤N≤105,
0≤ts,id≤105,
1≤D≤10000
输入样例:
7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3
输出样例:
1
3
双指针[j,i]理解为滑动窗口
维护大小为d的窗口
//有重复统计,就有优化【类似滑动窗口,进去一个+出来一个】
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII; const int N = 100010;int n, d, k;
PII logs[N]; // (ts,id)
int cnt[N];
bool st[N]; // 记录每个帖子是否是热帖int main()
{scanf("%d%d%d", &n, &d, &k);for (int i = 0; i < n; i ++ ) scanf("%d%d", &logs[i].x, &logs[i].y);sort(logs, logs + n);//【按时间ts排序】for (int i = 0, j = 0; i < n; i ++ )//[j, i]区间长度 <= d{int id = logs[i].y; cnt[id] ++ ; //统计区间内对应id收到的赞while (logs[i].x - logs[j].x >= d) //if(i位置当前赞 - j位置前一次赞 >= d时间跨度[区间长度限制]) j向前移动 【看做滑动窗口理解,窗口大小 = d】{cnt[logs[j].y] -- ;//j向前移动位置 ,原本的j位置出窗口, i在循环中i++ [类比最长连续不重复子序列]j ++ ;}if (cnt[id] >= k) st[id] = true; //id在满足小于时间跨度[区间长度限制]d获得>=k个赞}for (int i = 0; i <= 100000; i ++ )//输出满足热度的帖子的idif (st[i])printf("%d\n", i);return 0;
}
1209. 带分数
100 可以表示为带分数的形式:100=3+69258714
还可以表示为:100=82+3546197
注意特征:带分数中,数字 1∼9 分别出现且只出现一次(不包含 0)。
类似这样的带分数,100 有 11 种表示法。
输入格式
一个正整数。
输出格式
输出输入数字用数码 1∼9 不重复不遗漏地组成带分数表示的全部种数。
数据范围
1≤N<10610^6106
输入样例1:
100
输出样例1:
11
输入样例2:
105
输出样例2:
6
//y总思路:全排列 + 划分枚举a、c,判断b是否成立 ,等式 n == a + b / c
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 10;int n;
bool st[N], backup[N];
int ans;bool check(int a, int c)//检查b,等式是否成立
{ //可以开个全局LLlong long b = n * (long long)c - a * c; //n = a + b / c 鉴于int向上取整,两边同乘c避开int特性: n * (long long c) == a * c + bif (!a || !b || !c) return false; //a,b,c中含有0,falsememcpy(backup, st, sizeof st); //使用备份数组,复制原标记数组while (b){int x = b % 10; // 取个位b /= 10; // 个位删掉if (!x || backup[x]) return false; //x不为0且x被标记过(a或c已经使用),则b不能选此数,falsebackup[x] = true;}for (int i = 1; i <= 9; i ++ )//1-9没有全部用上,falseif (!backup[i])return false;return true;
}void dfs_c(int u, int a, int c) //当前位u , a的值 , c的值
{if (u > 9) return;if (check(a, c)) ans ++ ;for (int i = 1; i <= 9; i ++ )if (!st[i]){st[i] = true;dfs_c(u + 1, a, c * 10 + i);st[i] = false;}
}void dfs_a(int u, int a)//枚举a
{if (a >= n) return; //a > n 等式不成立,剪枝if (a) dfs_c(u, a, 0); for (int i = 1; i <= 9; i ++ )if (!st[i]){st[i] = true;dfs_a(u + 1, a * 10 + i); //判断下一组a,a加位数st[i] = false;}
}int main()
{cin >> n;dfs_a(0, 0);cout << ans << endl;return 0;
}
next_permutation
#include <bits/stdc++.h>
using namespace std;
int num[10] = {1,2,3,4,5,6,7,8,9}; //[1-9]
int cnt;int get(int l,int r) //区间[l, r]组成一个数
{int sum = 0;for(int i = l; i <= r; i++){sum = sum * 10 + num[i];}return sum;
}int main()
{int n;cin >> n;while(next_permutation(num, num + 9)) //【全排列】{for(int i = 0;i < 9; i++) //枚举a的位数{int a = get(0, i);for(int j = i + 1; j < 9; j++) //枚举b与c的分界位数{int b = get(i + 1, j); int c = get(j + 1, 8);if(n * c == a * c + b){cnt ++;}}}}cout << cnt;return 0;
}
🌲day3
844. 走迷宫
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8
#include <bits/stdc++.h>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 110;int n, m;int g[N][N], d[N][N]; //不用标记st【d[][] == -1 :未走过】
PII q[N * N];//空间大小N * N 组坐标元素int bfs() //宽搜从(0, 0)走到终点(n-1, m-1)
{int hh = 0, tt = -1;// memset(d, -1, sizeof d);int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};d[0][0] = 0;q[++ tt] = {0, 0};while(hh <= tt){auto t = q[hh ++];for(int i = 0; i < 4; i++){int a = t.x + dx[i], b = t.y + dy[i];// printf("%d %d\n", a, b);if(a >= 0 && a < n && b >= 0 && b < m && g[a][b] == 0){d[a][b] = d[t.x][t.y] + 1;q[ ++ tt] = {a, b};g[a][b] = 1;}}}return d[n - 1][m - 1];
}int main()
{scanf("%d%d", &n, &m); for(int i = 0 ; i < n; i++)for(int j = 0; j < m; j++)scanf("%d", &g[i][j]); printf("%d", bfs());return 0;
}
STL
#include <iostream>
#include <cstring>
#include <queue>
#include<stack>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 110;int n, m;
int g[N][N], d[N][N];
queue<PII> path;int bfs()
{queue<PII> q;memset(d, -1, sizeof d);d[0][0] = 0;q.push({0, 0});int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};while (q.size()){auto t = q.front();q.pop();for (int i = 0; i < 4; i ++ ){int x = t.first + dx[i], y = t.second + dy[i];if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;q.push({x, y});path.push({x, y});}}}int x, y;while(path.size())//queue<PII> path : FIFO先进先出 -正序输出 【若逆序存入,则用stack<PII> path : LIFO后进先出 -正序输出】{x = path.front().x, y = path.front().y;path.pop();printf("%d %d\n", x, y); //逆序输出路径 【正序改用栈stack<PII> path[N * N]存入】}return d[n - 1][m - 1];
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )scanf("%d", &g[i][j]);printf("%d", bfs());return 0;
}
1101. 献给阿尔吉侬的花束
阿尔吉侬是一只聪明又慵懒的小白鼠,它最擅长的就是走各种各样的迷宫。
今天它要挑战一个非常大的迷宫,研究员们为了鼓励阿尔吉侬尽快到达终点,就在终点放了一块阿尔吉侬最喜欢的奶酪。
现在研究员们想知道,如果阿尔吉侬足够聪明,它最少需要多少时间就能吃到奶酪。
迷宫用一个 R×C 的字符矩阵来表示。
字符 S 表示阿尔吉侬所在的位置,字符 E 表示奶酪所在的位置,字符 # 表示墙壁,字符 . 表示可以通行。
阿尔吉侬在 1 个单位时间内可以从当前的位置走到它上下左右四个方向上的任意一个位置,但不能走出地图边界。
输入格式
第一行是一个正整数 T,表示一共有 T 组数据。
每一组数据的第一行包含了两个用空格分开的正整数 R 和 C,表示地图是一个 R×C 的矩阵。
接下来的 R 行描述了地图的具体内容,每一行包含了 C 个字符。字符含义如题目描述中所述。保证有且仅有一个 S 和 E。
输出格式
对于每一组数据,输出阿尔吉侬吃到奶酪的最少单位时间。
若阿尔吉侬无法吃到奶酪,则输出“oop!”(只输出引号里面的内容,不输出引号)。
每组数据的输出结果占一行。
数据范围
1<T≤10,
2≤R,C≤200
输入样例:
3
3 4
.S..
###.
..E.
3 4
.S..
.E..
....
3 4
.S..
####
..E.
输出样例:
5
1
oop!
经典迷宫BFS
记bfs步骤:①初始化队列q和dist取-1 ,dist[start.x][start.y] = 0(x,y为define全局定义)起点start放入队列,方向向量dx[4](从-1开始) ,dy[4]②遍历所有元素依次入队,while(队不为空)③取队头,出队 , 遍历所有方向 ,依据题目判断边界,条件④放入对列 , 中间加个if(end== make_pair(x, y) ) return dist[x][y];判断直接结束
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>#define x first//pair的代码简化
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 210;int n, m;
char g[N][N];
int dist[N][N];int bfs(PII start, PII end)//bfs模板【STL队列版】
{queue<PII> q;memset(dist, -1, sizeof dist);//不可达则未更新,标记为-1dist[start.x][start.y] = 0;//0标记走过 q.push(start);//起点入队 int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//dx[4](从-1开始)模式化while (q.size()) {auto t = q.front();//取队头 q.pop();//出队 for (int i = 0; i < 4; i ++ ){int x = t.x + dx[i], y = t.y + dy[i];if (x < 0 || x >= n || y < 0 || y >= m || g[x][y] == '#' || dist[x][y] != -1) continue; // 出界 || 障碍物 || 已经走过 --> 判断下一个 dist[x][y] = dist[t.x][t.y] + 1;if (end == make_pair(x, y)) return dist[x][y]; //make_pair返回pair ,也可以放在最后返回distq.push({x, y});}}return -1;
}int main()
{int T;scanf("%d", &T);while (T -- ){scanf("%d%d", &n, &m);for (int i = 0; i < n; i ++ ) scanf("%s", g[i]);//按字符串读入每行PII start, end;//设置终点、起点, 寻找终点、起点for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )if (g[i][j] == 'S') start = {i, j};else if (g[i][j] == 'E') end = {i, j};int distance = bfs(start, end);//起点--->终点 if (distance == -1) puts("oop!");//返回-1未更新,不可达else printf("%d\n", distance);}return 0;
}🌲day4
1113. 红与黑
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。
你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。
请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式
输入包括多个数据集合。
每个数据集合的第一行是两个整数 W
和 H
,分别表示 x
方向和 y
方向瓷砖的数量。
在接下来的 H
行中,每行包括 W
个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出格式
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
数据范围
1≤W,H≤20
输入样例:
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
输出样例:
45
BFS
#include<bits/stdc++.h>
#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 25;int n, m;
char g[N][N];
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
PII q[N * N]; //【最多遍历所有点N * N】int bfs(int x, int y)
{int cnt = 1;int hh = 0, tt = -1;q[++tt] = {x, y};while(hh <= tt){auto t = q[hh++]; for(int i = 0; i < 4; i++){int a = t.x + dx[i], b = t.y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m && g[a][b] == '.') {g[a][b] = '#'; //【直接修改为障碍物-等效标记走过-不会重复统计】q[++tt] = {a, b};cnt ++;}}}return cnt;
}int main()
{while (cin >> m >> n, n || m){for (int i = 0; i < n; i ++ ) scanf("%s", g[i]); //读入一行int x, y;for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )if (g[i][j] == '@')//找到起点{x = i;y = j;}printf("%d\n", bfs(x, y));}return 0;
}
DFS
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 25;int n, m;
char g[N][N];
bool st[N][N];//int ne[4][2] = {{-1,0}, {0,1}, {1,0}, {0,-1}};
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};int dfs(int x, int y)//起点开始
{int cnt = 1;st[x][y] = true;for (int i = 0; i < 4; i ++ ){int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m) continue;//合并: if(越界 || 不是黑色 || 标记走过) continue; 判断下一个 if (g[a][b] != '.') continue;if (st[a][b]) continue;cnt += dfs(a, b);//能到的点的数量【看成树:则为加上所有叶子节点数量】}return cnt;
}int main()
{while (cin >> m >> n, n || m) //所有表达式都会执行,只不过返回值是最后一个表达式的值{for (int i = 0; i < n; i ++ ) cin >> g[i];int x, y;for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )if (g[i][j] == '@')//起点{x = i;y = j;}memset(st, 0, sizeof st);//多组数据,每次要把标记数组清空一遍cout << dfs(x, y) << endl;}return 0;
}
🌲day5
1236. 递增三元组
给定三个整数数组
A=[A1,A2,…AN],
B=[B1,B2,…BN],
C=[C1,C2,…CN],
请你统计有多少个三元组 (i,j,k)
满足:
1≤i,j,k≤N
Ai<Bj<Ck
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,…AN。
第三行包含 N 个整数 B1,B2,…BN。
第四行包含 N 个整数 C1,C2,…CN。
输出格式
一个整数表示答案。
数据范围
1≤N≤105,
0≤Ai,Bi,Ci≤105
输入样例:
3
1 1 1
2 2 2
3 3 3
输出样例:
27
暴力:for三重 if(a[i] < b[i] && b[i] < c[i])res++;
通过时间复杂度需限制再O(nlogn) 则只能枚举一个数组 ,应枚举B[i],因为A[i]与C[i]只需被B[i]限制
再把A、C中满足的个数相乘 [等效满足的A<B<C的组合]
实现:O(n)法①:前缀和 O(nlogn)法②:sort(A) + 二分法(B[j])找到A中小于B[j]的下标res :答案个数就为 res + 1
前缀和映射hash有减1操作,但有数值0的,所以每位加1,取值映射变为[1,1e5 + 1],(相对大小不变)
把数值映射为hash值 , 前缀和数组存储值小于当前下标的个数,同理c就存储大于当前下标的个数【类似桶排序】
前缀和实现
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;const int N = 100010;int n;
int a[N], b[N], c[N];
int as[N]; // as[i]表示在A[]中有多少个数小于b[i]
int cs[N]; // cs[i]表示在C[]中有多少个数大于b[i]
int cnt[N], s[N];//cnt[]存a的值的数量int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]), a[i] ++ ;for (int i = 0; i < n; i ++ ) scanf("%d", &b[i]), b[i] ++ ;for (int i = 0; i < n; i ++ ) scanf("%d", &c[i]), c[i] ++ ;// 求as[]for (int i = 0; i < n; i ++ ) cnt[a[i]] ++ ;//将数组a中所有元素出现的次数存入一个哈希表中for (int i = 1; i < N; i ++ ) s[i] = s[i - 1] + cnt[i]; // 求cnt[]的前缀和for (int i = 0; i < n; i ++ ) as[i] = s[b[i] - 1];//a[]中小于b[i]的元素个数前缀和 :前缀和s可表示为不超过下标值的元素个数(所以减1)// 求cs[]memset(cnt, 0, sizeof cnt);memset(s, 0, sizeof s);for (int i = 0; i < n; i ++ ) cnt[c[i]] ++ ;//将数组c中所有元素出现的次数存入一个哈希表中for (int i = 1; i < N; i ++ ) s[i] = s[i - 1] + cnt[i];for (int i = 0; i < n; i ++ ) cs[i] = s[N - 1] - s[b[i]]; //s[N-1] - s[b[i]]表示:c[]所有元素中大于b[i]的个数// 枚举每个b[i]LL res = 0;for (int i = 0; i < n; i ++ ) res += (LL)as[i] * cs[i];//1e5*1e5 会爆int 开LLcout << res << endl;return 0;
}
简版STL
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int a[N], b[N], c[N];int main()
{int n;scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%d", &a[i]);for(int i = 0; i < n; i++) scanf("%d", &b[i]);for(int i = 0; i < n; i++) scanf("%d", &c[i]);sort(a, a + n), sort(b, b + n), sort(c, c + n);LL cnt = 0;for(int i = 0; i < n; i++) //b比a大 且 比c小 - 【枚举b[] 乘积 {LL A = lower_bound(a, a + n, b[i]) - a; //a[]中第一个大等于b[i]的位置 (从0开始刚好 个数 == 下标) LL C = n - (upper_bound(c, c + n, b[i]) - c); //c[]中第一个小于b的位置 (剩下均大于b[i]) cnt += A * C;}printf("%lld", cnt);return 0;
}
三指针
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int a[N], b[N], c[N];int main()
{int n;scanf("%d", &n);for(int i = 0; i < n; i++) scanf("%d", &a[i]);for(int i = 0; i < n; i++) scanf("%d", &b[i]);for(int i = 0; i < n; i++) scanf("%d", &c[i]);sort(a, a + n), sort(b, b + n), sort(c, c + n);LL sum = 0,s1 = 0,s2 = 0;for(int i=0;i<n;i++){while(s1 < n && a[s1] < b[i]) s1++;while(s2 < n && c[s2] <= b[i]) s2++;sum += s1 * (n - s2);}printf("%lld", sum);return 0;
}
🌲day6
3491. 完全平方数[简单数论]
一个整数 a 是一个完全平方数,是指它是某一个整数的平方,即存在一个整数 b,使得 a=b2b^2b2。
给定一个正整数 n,请找到最小的正整数 x,使得它们的乘积是一个完全平方数。
输入格式
输入一行包含一个正整数 n。
输出格式
输出找到的最小的正整数 x。
数据范围
对于 30%
的评测用例,1≤n≤1000,答案不超过 1000。
对于 60% 的评测用例,1≤n≤10810^8108,答案不超过 10810^8108。
对于所有评测用例,1≤n≤101210^{12}1012,答案不超过 101210^{12}1012。
输入样例1:
12
输出样例1:
3
输入样例2:
15
输出样例2:
15
质因子的次数为偶数 — 则为平方数 — 解法等效让所有质因子为偶数 还需乘上哪些质因子
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long LL; //1e12int main()
{LL n;cin >> n;LL res = 1;for (LL i = 2; i * i <= n; i ++ ) //模板if (n % i == 0){int s = 0;while (n % i == 0) s ++, n /= i; //统计质因子i个数s, n除去质因子iif (s % 2) res *= i; //i为奇数,则乘上一个i变为偶数}if (n > 1) res *= n; //【还有一个为奇数的质因子】cout << res << endl;return 0;
}
🌲day7
466. 回文日期
(枚举,模拟) O(104)O(10^4)O(104)
由于只有八位数,而且回文串左右对称,因此可以只枚举左半边,这样只需枚举 0∼9999总共一万个数,然后判断:
①枚举回文串
②是否在给定范围[date1,date2]内
③日期是否合法;
时间复杂度:一共枚举 10410^4104 个数,判断每个数是否合法的计算量是常数级别的,因此总计算量是 O(104)O(10^4)O(104)。
【想法】
%10n10^n10n : 取末尾n位
/10n10^n10n : 删除末尾n位
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;int months[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};bool check(int date)//检查年月日是否合法
{int year = date / 10000;int month = date % 10000 / 100;//%10000等效取后四位 ,/100删去后两位 int day = date % 100;if (!month || month >= 13 || !day) return false;if (month != 2 && day > months[month]) return false;//先不管二月if (month == 2)//特判二月{bool leap = year % 4 == 0 && year % 100 || year % 400 == 0;//是否闰年if (day > 28 + leap) return false;}return true;
}int main()
{int date1, date2;cin >> date1 >> date2;int res = 0;for (int i = 0; i < 10000; i ++ ){int x = i, r = i;for (int j = 0; j < 4; j ++ ) r = r * 10 + x % 10, x /= 10;//拼接,取最后一位加上 + 原数值乘10 如:1234 --> 12344321 if (r >= date1 && r <= date2 && check(r)) res ++ ;//检查是否在区间[date1,date2]内}printf("%d\n", res);return 0;
}
相关文章:

蓝桥杯冲刺 - week1
文章目录💬前言🌲day192. 递归实现指数型枚举843. n-皇后问题🌲day2日志统计1209. 带分数🌲day3844. 走迷宫1101. 献给阿尔吉侬的花束🌲day41113. 红与黑🌲day51236. 递增三元组🌲day63491. 完全…...

Leetcode27. 移除元素
目录一、题目描述:二、解决思路和代码1. 解决思路2. 代码一、题目描述: 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用…...
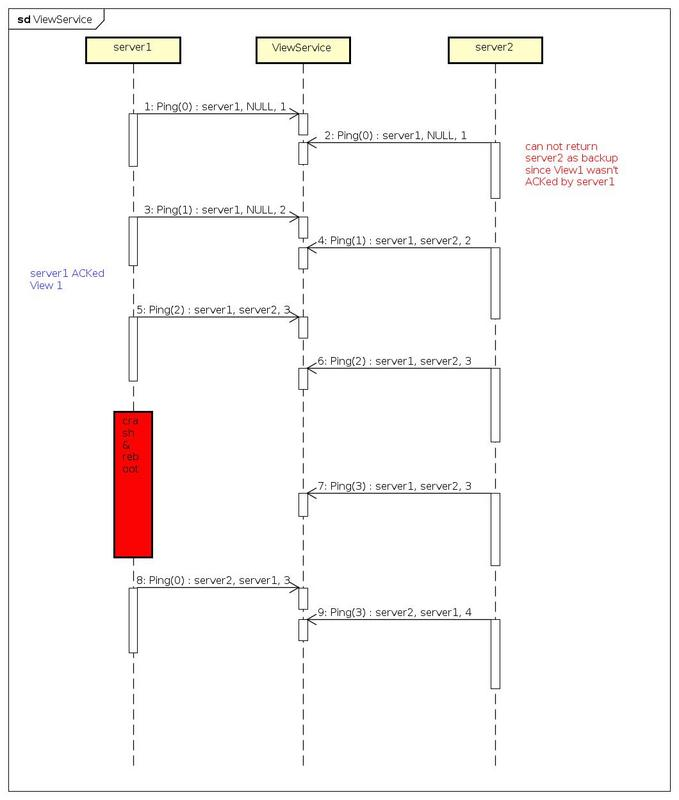
ViewService——一种保证客户端与服务端同步的方法
简介在分布式系统中,最常见的场景就是主备架构。但是如果主机不幸宕机,如何正确的通知客户端当前后端服务器的状况成为一个值得研究的问题。本文描述了一种简单的模型用于解决此问题。背景以一个分布式的Key-Value数据库为背景。数据库对外提供3个接口Ge…...

使用STM32F103ZE开发贪吃蛇游戏
目录 前言 一、设置FreeROTS用户任务 (1)事件event任务 (2)按键输入方向控制任务 (3)果实食物任务 (4)显示任务函数 (3)开始任务 二、主函数 三、ADC采样…...

如何利用Web3D技术打造在线虚拟展览馆
随着Web3D技术的不断发展,越来越多的企业和组织开始将其应用于虚拟展览馆的建设中。虚拟展览馆可以为观众提供高度沉浸式的展览体验,让观众可以随时随地参观各种展览,同时也为展览组织者提供了更多的展示方式和机会。下面将介绍如何利用Web3D…...

第二十三章 opengl之高级OpenGL(实例化)
OpenGL实例化实例化数组绘制小行星带实例化 综合应用。 如果绘制了很多的模型,但是大部分的模型包含同一组顶点数据,只是不同的世界空间变换。 举例:一个全是草的场景,每根草都是一个包含了几个小三角形的模型。需要绘制很多根草…...

C++ String类总结
头文件 #include <string>构造函数 default (1) basic_string();explicit basic_string (const allocator_type& alloc); copy (2) basic_string (const basic_string& str);basic_string (const basic_string& str, const allocator_type& alloc); su…...

内网升级“高效安全”利器!统信软件发布私有化更新管理平台
随着数字化的深度推进,信息安全重要性进一步凸显。建设自主可控的国产操作系统,提升信息安全自主能力,已成为国家重要战略之一。 操作系统安全对计算机系统的整体安全发挥着关键作用,各类客户往往需要在第一时间获取更新与安全补…...
JAVA开发(自研项目的开发与推广)
https://live.csdn.net/v/284629 案例背景: 作为JAVA开发人员,我们可以开发无数多的web项目,电商系统,小程序,H5商城。有时候作为技术研发负责人,项目做成了有时候也需要对内进行内测,对外进行…...
Mysql用户权限分配详解
文章目录MySQL 权限介绍一、Mysql权限级别分析(1)全局级别(1.1) USER表的组成结构(1.1.1) 用户列(1.1.2) 权限列(1.1.3) 安全列(1.1.4)…...

【TypeScript 入门】13.枚举类型
枚举类型 枚举类型:定义包含被命名的常量的集合。比如 TypeScript 支持枚举数字、字符两种常量值类型。 使用方式: enum + 枚举名字 + 花括弧包裹被命名了的常量成员: enum Size {S,M,L } const a = Size.M console.log(Size, Size)...
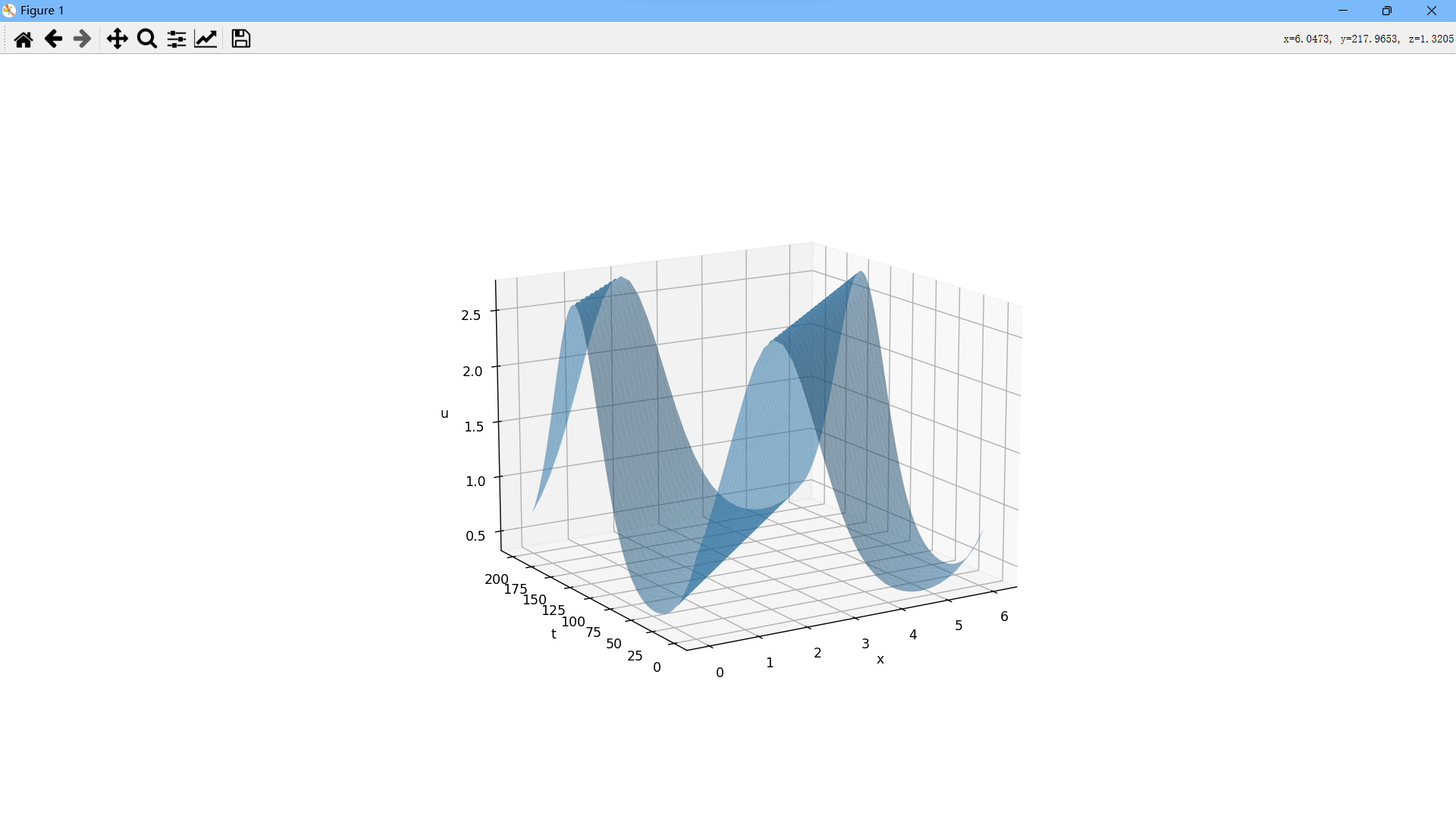
Python科学计算:偏微分方程1
首先,我们来看初边值问题:伯格斯方程:假设函数是定义在上的函数,且满足:右侧第一项表示自对流,第二项则表示扩散,在许多物理过程中,这两种效应占据着主导地位,为了固定一…...
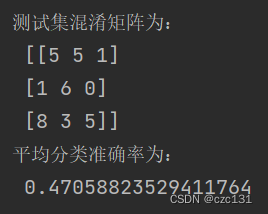
PLS-DA分类的实现(基于sklearn)
目录 简单介绍 代码实现 数据集划分 选择因子个数 模型训练并分类 调用函数 简单介绍 (此处取自各处资料) PLS-DA既可以用来分类,也可以用来降维,与PCA不同的是,PCA是无监督的,PLS-DA是有监督的…...
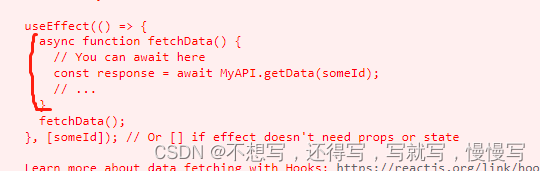
常用hook
Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。理解:hook是react提供的函数API官方提供的hook基础hookuseState APIconst [state, setState] useState(initialState); //返回state值 以及更新state的方法 …...
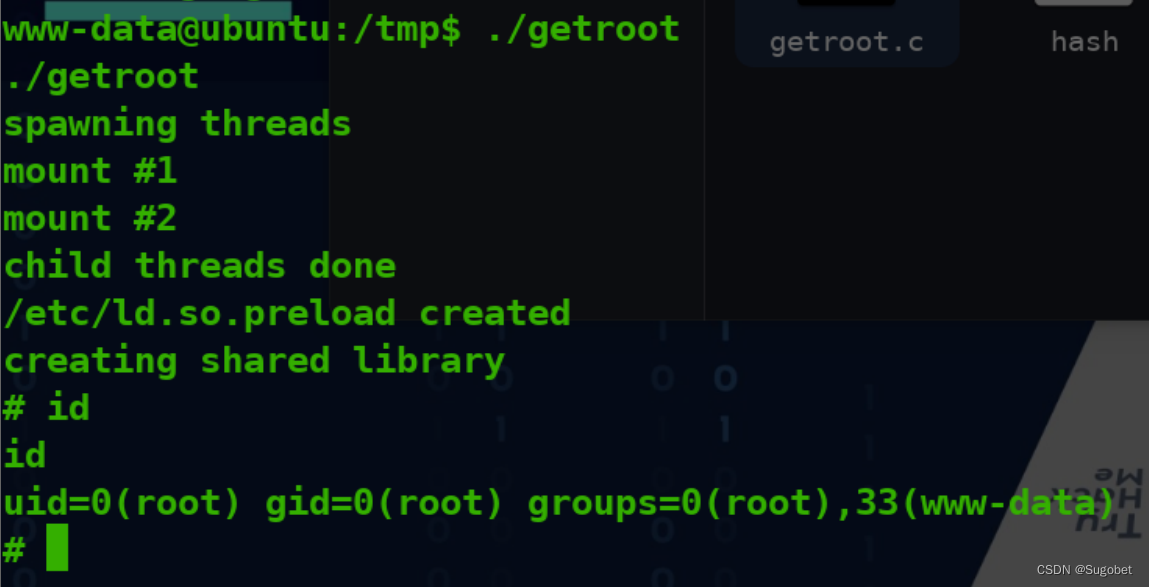
TryHackMe-GoldenEye(boot2root)
GoldenEye 这个房间将是一个有指导的挑战,以破解詹姆斯邦德风格的盒子并获得根。 端口扫描 循例nmap Web枚举 进入80 查看terminal.js 拿去cyberchef解码 拿着这组凭据到/sev-home登录 高清星际大战 POP3枚举 使用刚刚的凭据尝试登录pop3 使用hydra尝试爆破 这…...
Elasticsearch基本安全加上安全的 HTTPS 流量
基本安全加上安全的 HTTPS 流量 在生产环境中,除非您在 HTTP 层启用 TLS,否则某些 Elasticsearch 功能(例如令牌和 API 密钥)将被禁用。这个额外的安全层确保进出集群的所有通信都是安全的。 当您在模式下运行该elasticsearch-ce…...
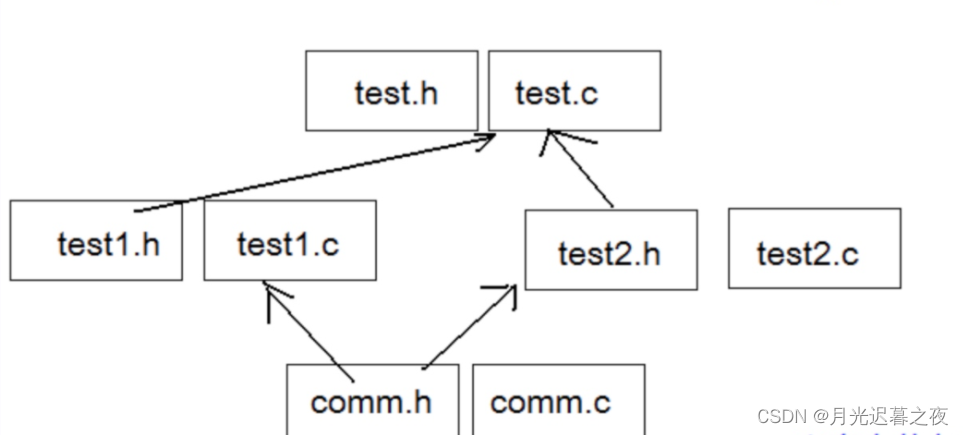
C语言-程序环境和预处理(2)
文章目录预处理详解1.预定义符号2.#define2.1#define定义的标识符2.2#define定义宏2.3#define替换规则注意事项:2.4#和###的作用##的作用2.5带副作用的宏参数2.6宏和函数的对比宏的优势:宏的劣势:宏和函数的一个对比命名约定3.undef4.条件编译…...
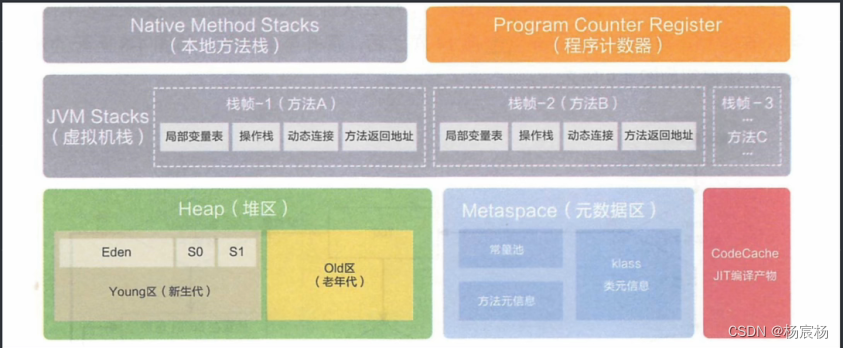
JVM 收集算法 垃圾收集器 元空间 引用
文章目录JVM 收集算法标记-清除算法标记-复制算法标记-整理算法JVM垃圾收集器Serial收集器ParNew收集器Parallel Scavenge /Parallel Old收集器CMS收集器Garbage First(G1)收集器元空间引用强引用软引用弱引用虚引用JVM 收集算法 前面我们了解了整个堆内存实际是以分代收集机制…...
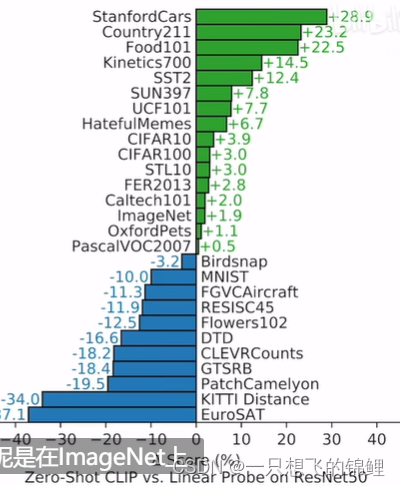
clip精读
开头部分 1. 要点一 从文章题目来看-目的是:使用文本监督得到一个可以迁移的 视觉系统 2.要点二 之前是 fix-ed 的class 有诸多局限性,所以现在用大量不是精细标注的数据来学将更好,利用的语言多样性。——这个方法在 nlp其实广泛的存在&…...
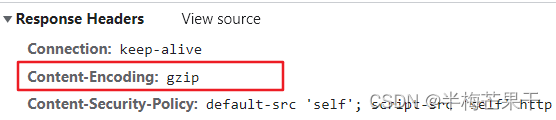
vue 首次加载慢优化
目前使用的是vue2版本 1.路由懒加载(实现按需加载) component: resolve > require([/views/physicalDetail/index], resolve)2.gzip压缩插件(需要运维nginx配合) 第一步,下载compression-webpack-plugin cnpm i c…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
