PLS-DA分类的实现(基于sklearn)
目录
简单介绍
代码实现
数据集划分
选择因子个数
模型训练并分类
调用函数
简单介绍
(此处取自各处资料)
PLS-DA既可以用来分类,也可以用来降维,与PCA不同的是,PCA是无监督的,PLS-DA是有监督的。与PCA不同,PCA是无监督,PLS是“有监督”模式的偏最小二乘法分析,当样本组间差异大而组内差异小时,无监督分析方法可以很好的区分组间差异。反之样本组间差异不大,无监督的方法就难以区分组间差异。另外如果组间的差异较小,各组的样本量相差较大,样本量大的那组将会主导模型。有监督的分析(PLS-DA)能够很好的解决这些问题。也就是在分析数据时,已知样本的分组关系,这样可以更好的选择区分各组的特征变量,确定样本之间的关系。DA是判别分析,PLS-DA用偏最小二乘回归的方法,在对数据“降维”的同时,建立了回归模型,并对回归结果进行判别分析。
本文主要是基于PLS的分类展开。
代码实现
主要参考了这位大佬的: https://zhuanlan.zhihu.com/p/374412915
数据集划分
首先要把数据集处理成一定的格式,也就是把自变量和因变量搞清楚,做好数据集的分割,然后传回。
def deal_data(path):# 读取自变量和因变量构成的数据矩阵,类别y放最后一列,前面均为xspec = pd.read_excel(path)spec = np.array(spec) # 直接转化为numpy类型x = spec[:, 0:-1] # 前面的列均为自变量y = spec[:,-1]# 先做一个数据集的划分train_X, test_X, train_y, test_y = train_test_split(x, y, test_size=0.2)return train_X, test_X, train_y, test_y选择因子个数
PLS类似于PCA,是有成分这么一个说法的,不同的成分个数最终得到的效果也不一样,因此我们对于不同的成分个数均进行训练,然后进行交叉验证,观察不同成分个数的表现,从而选择合适的个数。
def accuracy_component(xc, xv, yc, yv, component=8, n_fold=5):# xc表示训练集,xv表示测试集,yc表示训练标签,yv表示测试标签,component表示最多个数,n_fold表示分为几组样本(每次一组作为测试集,交叉验证)k_range = np.linspace(start=1, stop=component, num=component)kf = KFold(n_splits=n_fold, random_state=None, shuffle=True) # n_splits表示要分割为多少个K子集,交叉验证需要accuracy_validation = np.zeros((1, component)) # 用于存储各个成分数的测试平均精准度accuracyaccuracy_train = np.zeros((1, component)) # 用于存储各个成分数的训练平均精准度accuracyfor j in range(component): # j∈[0,component-1],j+1∈[1,component]p = 0acc = 0 # acc表示总的精准度,p表示个数,acc/p平均精确度# 下面是普通训练model_pls = PLSRegression(n_components=j + 1) # 此时选择component个成分yc_labels = pd.get_dummies(yc)model_pls.fit(xc, yc_labels)y_pred = model_pls.predict(xv)y_pred = np.array([np.argmax(i) for i in y_pred])accuracy_train[:, j] = accuracy_score(yv, y_pred) # 这是直接训练的# 下面是交叉验证for train_index, test_index in kf.split(xc): # 进行n_fold轮交叉验证# 划分数据集X_train, X_test = xc[train_index], xc[test_index]y_train, y_test = yc[train_index], yc[test_index]YC_labels = pd.get_dummies(y_train) # 训练数据结果独热编码model_1 = PLSRegression(n_components=j + 1)model_1.fit(X_train, YC_labels)Y_pred = model_1.predict(X_test)Y_pred = np.array([np.argmax(i1) for i1 in Y_pred]) # 独热编码转化成类别变量acc = accuracy_score(y_test, Y_pred) + accp = p + 1accuracy_validation[:, j] = acc / p # 计算j+1个成分的平均精准度# 首先对于每个component数训练一个模型,然后利用测试集得出准确率print('模型训练的准确率')print(accuracy_train)# 然后对样本的训练集进行交叉验证print('交叉验证的平均准确率')print(accuracy_validation)plt.plot(k_range, accuracy_train.T, 'o-', label="Training", color="r")plt.plot(k_range, accuracy_validation.T, 'o-', label="Cross-validation", color="b")plt.xlabel("N components")plt.ylabel("Score")plt.legend(loc="best") # 选取最佳位置标注图注plt.rc('font', family='Times New Roman')plt.rcParams['font.size'] = 10plt.show()return accuracy_validation, accuracy_train下面是运行效果,因为数据是乱造的所以参数就不用关注了,这样来看的话三到四个因子效果还不错。
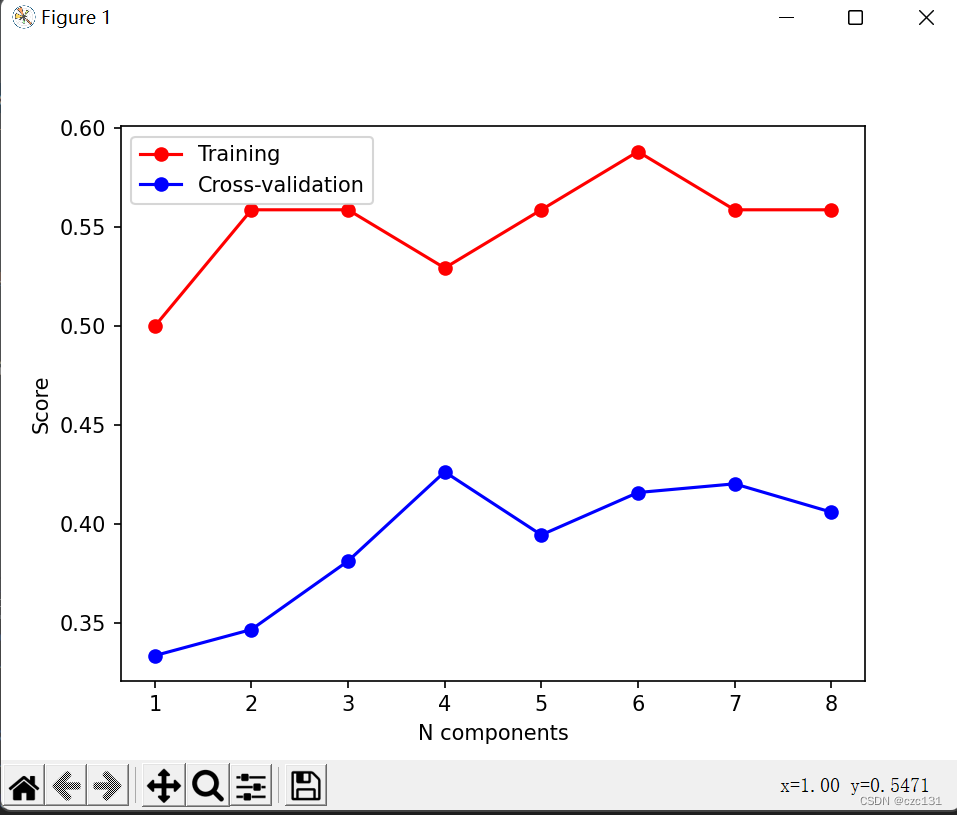
模型训练并分类
下面就是选择合适的成分个数进行分类,得到混淆矩阵和一些参数指标。
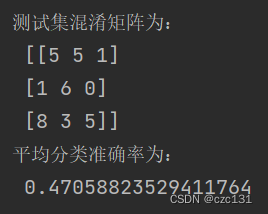
def PLS_DA(train_X, test_X, train_y, test_y):# 建模model = PLSRegression(n_components=6)train_y = pd.get_dummies(train_y)model.fit(train_X, train_y)# 预测y_pred = model.predict(test_X)# 将预测结果(类别矩阵)转换为数值标签y_pred = np.array([np.argmax(i) for i in y_pred])# 模型评价---混淆矩阵和精度print('测试集混淆矩阵为:\n', confusion_matrix(test_y, y_pred))print('平均分类准确率为:\n', accuracy_score(test_y, y_pred))
运行效果,至少比乱分类的33%正确率要高。
调用函数
以上都是各个组件,最后需要一个主函数调用串联起来,如下, 建议分步调用,也便于问题的发现和处理。
max_component = 8 # 迭代最大成分数
n_fold = 10 # 交叉验证次数
excel_path = './data.xlsx' # 数据集地址
if __name__ == '__main__':train_X, test_X, train_y, test_y = deal_data(excel_path) # 处理数据,返回处理完的训练和测试集,具体情况具体分析# accuracy_component(train_X, test_X, train_y, test_y, max_component, n_fold)PLS_DA(train_X, test_X, train_y, test_y,n_components=3)相关文章:

PLS-DA分类的实现(基于sklearn)
目录 简单介绍 代码实现 数据集划分 选择因子个数 模型训练并分类 调用函数 简单介绍 (此处取自各处资料) PLS-DA既可以用来分类,也可以用来降维,与PCA不同的是,PCA是无监督的,PLS-DA是有监督的…...
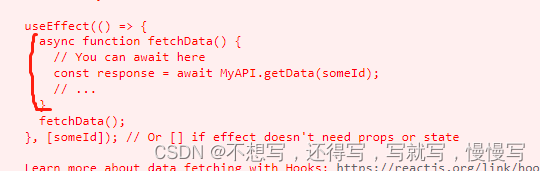
常用hook
Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。理解:hook是react提供的函数API官方提供的hook基础hookuseState APIconst [state, setState] useState(initialState); //返回state值 以及更新state的方法 …...
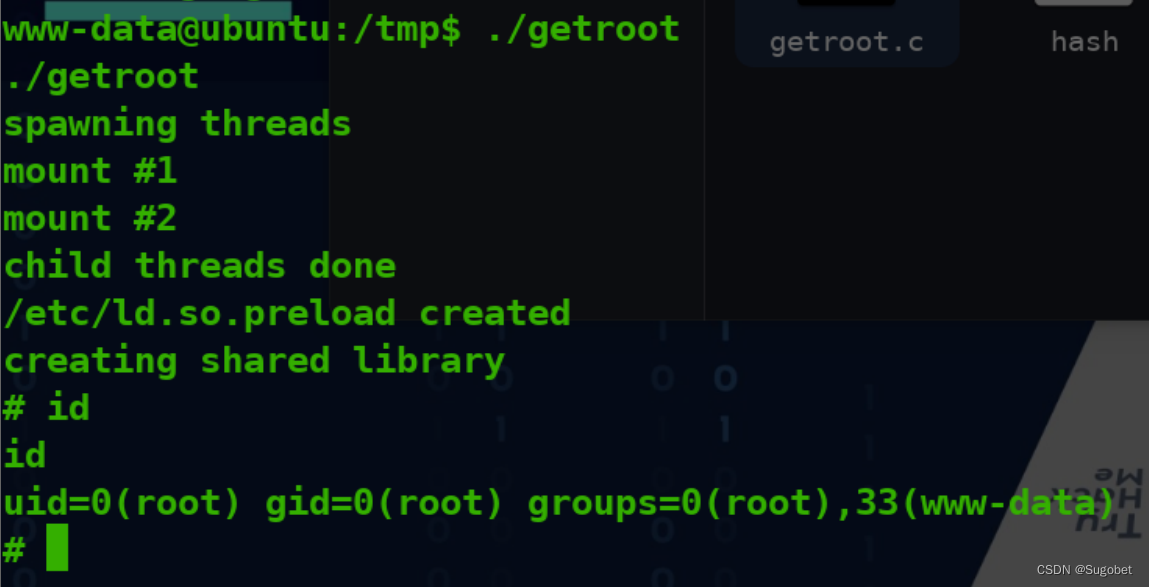
TryHackMe-GoldenEye(boot2root)
GoldenEye 这个房间将是一个有指导的挑战,以破解詹姆斯邦德风格的盒子并获得根。 端口扫描 循例nmap Web枚举 进入80 查看terminal.js 拿去cyberchef解码 拿着这组凭据到/sev-home登录 高清星际大战 POP3枚举 使用刚刚的凭据尝试登录pop3 使用hydra尝试爆破 这…...
Elasticsearch基本安全加上安全的 HTTPS 流量
基本安全加上安全的 HTTPS 流量 在生产环境中,除非您在 HTTP 层启用 TLS,否则某些 Elasticsearch 功能(例如令牌和 API 密钥)将被禁用。这个额外的安全层确保进出集群的所有通信都是安全的。 当您在模式下运行该elasticsearch-ce…...
C语言-程序环境和预处理(2)
文章目录预处理详解1.预定义符号2.#define2.1#define定义的标识符2.2#define定义宏2.3#define替换规则注意事项:2.4#和###的作用##的作用2.5带副作用的宏参数2.6宏和函数的对比宏的优势:宏的劣势:宏和函数的一个对比命名约定3.undef4.条件编译…...
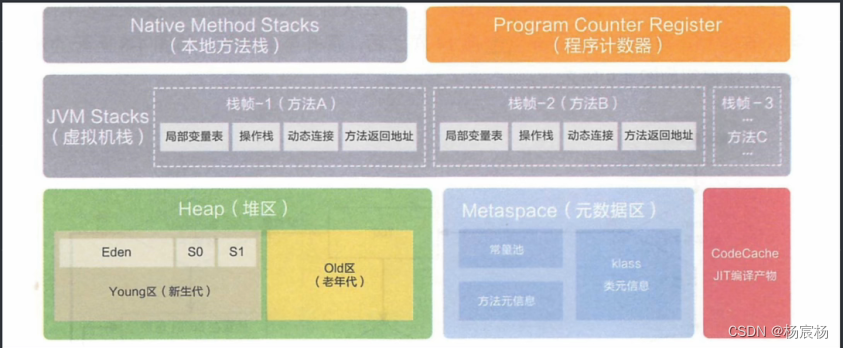
JVM 收集算法 垃圾收集器 元空间 引用
文章目录JVM 收集算法标记-清除算法标记-复制算法标记-整理算法JVM垃圾收集器Serial收集器ParNew收集器Parallel Scavenge /Parallel Old收集器CMS收集器Garbage First(G1)收集器元空间引用强引用软引用弱引用虚引用JVM 收集算法 前面我们了解了整个堆内存实际是以分代收集机制…...
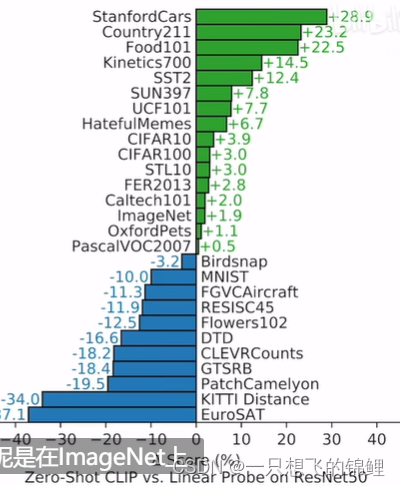
clip精读
开头部分 1. 要点一 从文章题目来看-目的是:使用文本监督得到一个可以迁移的 视觉系统 2.要点二 之前是 fix-ed 的class 有诸多局限性,所以现在用大量不是精细标注的数据来学将更好,利用的语言多样性。——这个方法在 nlp其实广泛的存在&…...
vue 首次加载慢优化
目前使用的是vue2版本 1.路由懒加载(实现按需加载) component: resolve > require([/views/physicalDetail/index], resolve)2.gzip压缩插件(需要运维nginx配合) 第一步,下载compression-webpack-plugin cnpm i c…...

WuThreat身份安全云-TVD每日漏洞情报-2023-03-21
漏洞名称:CairoSVG 文件服务器端请求伪造 漏洞级别:严重 漏洞编号:CVE-2023-27586 相关涉及:CairoSVG 在 2.7.0 版本之前 漏洞状态:POC 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-06718 漏洞名称:WP Meta SEO WordPress 授权不当导致任意重定向 漏洞级…...
【Android -- 开发工具】Xshell 6 安装和使用教程
一、简介 Xshell 其实就是一个远程终端工具,它可以将你的个人电脑和你在远端的机器连接起来,通过向 Xshell 输入命令然后他通过网络将命令传送给远端Linux机器然后远端的Linux机器将其运行结果通过网络传回个人电脑。 二、Xshell 6 的安装 首先&#…...

国民技术RTC备份寄存器RTC_BKP
根据手册资料知道RTC_BKP的地址,代码如下 #include "main.h" #include "usart.h"void USART2_Configuration(void) {USART_InitType USART_InitStructure;GPIO_InitType GPIO_InitStructure;GPIO_InitStruct(&GPIO_InitStructure);RCC_Ena…...
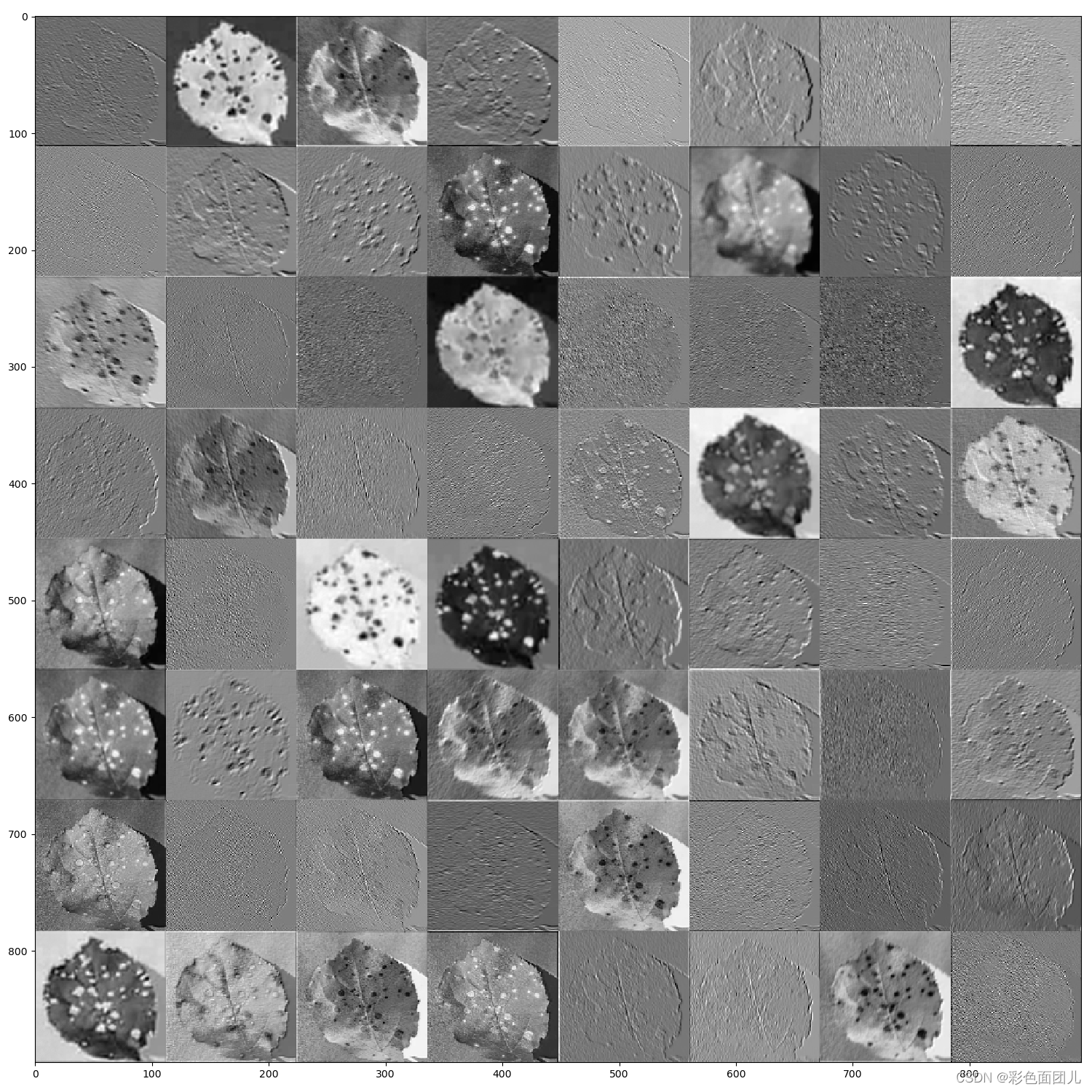
resnet网络特征提取过程可视化
我们在训练图片时,是不是要看看具体提取时的每个特征图提取的样子,找了很多,终于功夫不负有心人,找到了,通过修改的代码: resnet代码: import torch import torch.nn as nn from torchvision…...
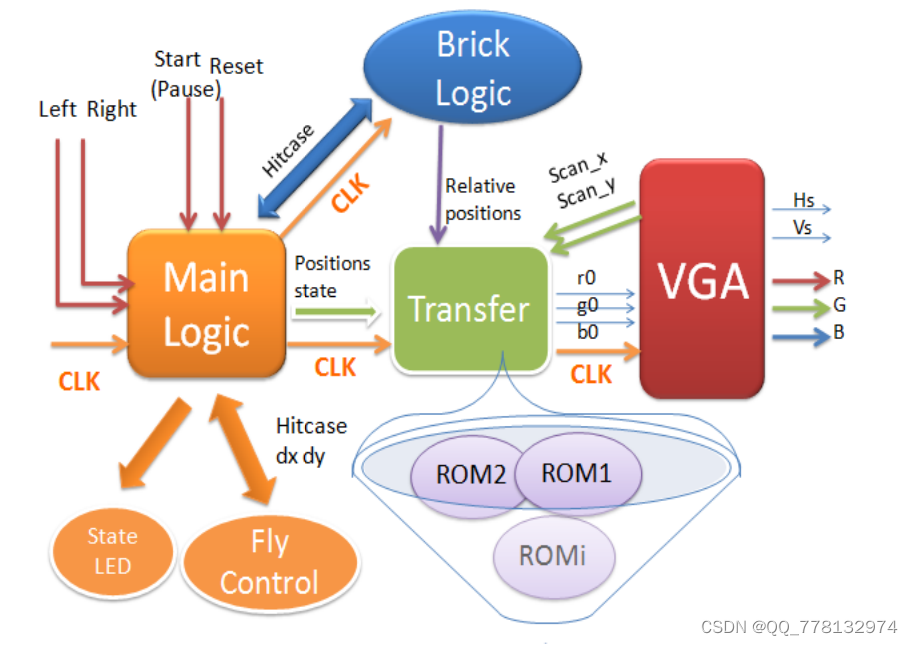
FPGA打砖块游戏设计(有上板照片)VHDL
这是一款经典打砖块游戏,我们的努力让它更精致更好玩,我们将它取名为打砖块游戏(Flyball),以下是该系统的一些基本功能: 画面简约而经典,色彩绚丽而活泼,动画流畅 玩家顺序挑战3个不同难度的级别,趣味十足 计分功能,卡通字母数字 4条生命值,由生命条显示…...

【Unity入门】3D物体
【Unity入门】3D物体 大家好,我是Lampard~~ 欢迎来到Unity入门系列博客,所学知识来自B站阿发老师~感谢 (一)物体移动旋转缩放 (1)物体移动 在上一篇文章【Unity入门】场景视图操作我们学会了在场景中创建3…...
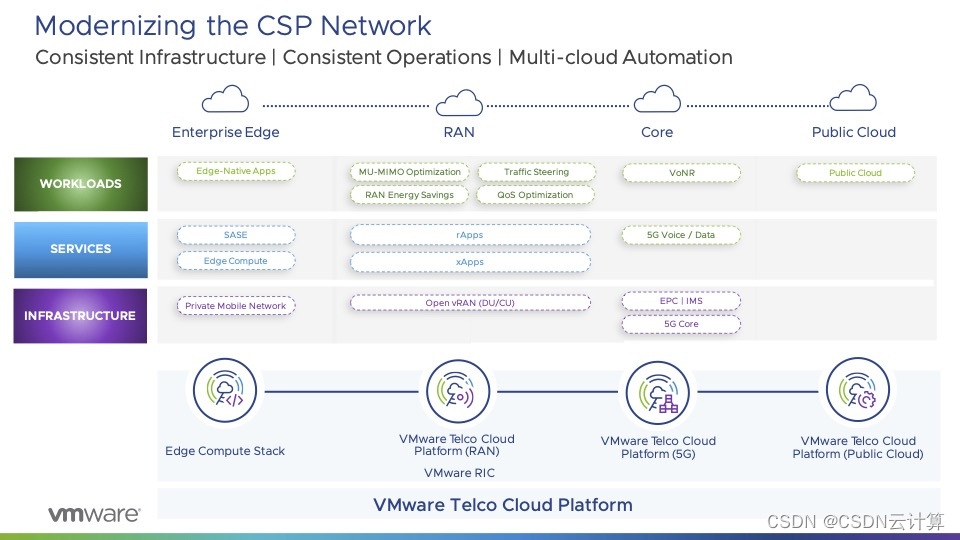
网络现代化势在必行,VMware 发布软件定义网络 SD-WAN 全新方案
出品 | CSDN云计算 作为计算存储网络基础设施三大件之一,网络一直是 IT 核心技术,并不断向前发展。 数字化转型浪潮下,各行业都在探索创新应用,而数字化创新,也是对 5G 和云边端等网络基础设施提出更高需求,…...

java学习笔记——抽象类
2.1 概述 由来 父类中的方法,被他的子类们重写,子类各自的实现都不尽相同。那么父类的方法声明和方法主体,只有声明还有意义,而方法主体则没有存在的意义了。我们把没有主体的方法称为抽象方法。java语法规定,包含抽象…...

Redis删除策略
删除策略就是针对已过期数据的处理策略。 针对过期数据要进行删除的时候都有哪些删除策略呢? 1.定时删除2.惰性删除3.定期删除1、立即删除 当key设置有过期时间,且过期时间到达时,由定时器任务立即执行对键的删除操作。 优点:节…...

【新星计划2023】SQL SERVER (01) -- 基础知识
【新星计划2023】SQL SERVER -- 基础知识1. Introduction1.1 Official Website1.2 Conn Tool2. 基础命令2.1 建库建表2.2 Alter2.3 Drop2.3 Big Data -- Postgres3.Awakening1. Introduction 1.1 Official Website 官方文档(小技巧) Officail Website: …...
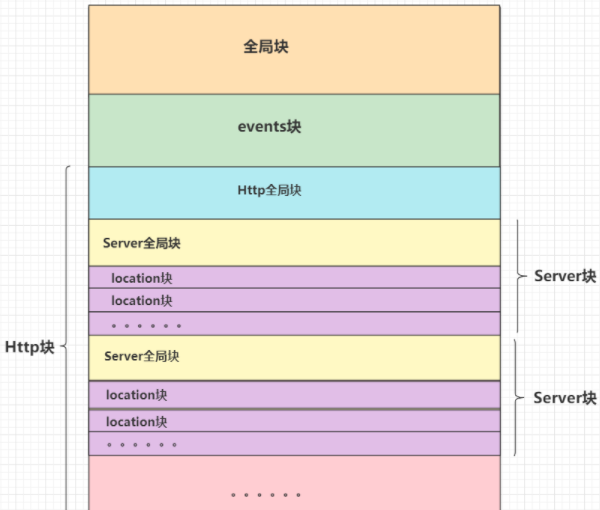
nginx配置详解
一.nginx常用命令1.Windows(1).查看nginx的版本号nginx -v(2).启动nginxstart nginx(3).快速停止或关闭nginxnginx -s stop(4).正常停止或关闭nginxnginx -s quit(5).配置文件nginx.conf修改重装载命令nginx -s reload2.Linux(1).进入 nginx 目录中cd /usr/local/nginx/sbin(2)…...

关于Java中堆和栈的学习
文章目录1.概述1.1 堆1.2 栈2.堆内存2.1 什么是堆内存?2.2堆内存的特点是什么?2.3new对象在堆中如何分配?3.栈内存3.1什么是栈内存?3.2栈内存的特点3.3栈内存的内存分配机制3.4数据共享4.栈与堆的区别4.1差异4.2相同5. 面试题: java堆和栈的区别**申请方式****申请后系统的…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
