Python科学计算:偏微分方程1
首先,我们来看初边值问题:伯格斯方程:
假设函数 是定义在
是定义在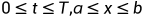 上的函数,且满足:
上的函数,且满足:

右侧第一项表示自对流,第二项则表示扩散,在许多物理过程中,这两种效应占据着主导地位,为了固定一个特定的解,我们对其施加一个初始条件:

以及一个或者多个边值条件:

由上面的三个式子所组成的问题被称为初边值问题(IBVP),如果我们同时设置a为-inf,b为 inf,那么我们会得到一个初值问题(IVP)
这里主要介绍两个比较常用的方法:
1、有限差分空间导数:我们选用有限组等距值 来表示区间
来表示区间
其中步长 ,那么我们根据导数的定义,可以得到:
,那么我们根据导数的定义,可以得到:

以及:

这样的话,我们就可以用前向欧拉方法来计算,但是,这样的话,我们就要进行稳定性分析(之前的博客里面是有的),为了保证显式时间步进是稳定的,就要确保: ,其中C是一个同阶常数,那么从这里我们实际上可以看得到:显式差分的时间步长收到了空间步长的制约,这是显式差分的一个弊病。
,其中C是一个同阶常数,那么从这里我们实际上可以看得到:显式差分的时间步长收到了空间步长的制约,这是显式差分的一个弊病。
2、周期问题的谱技术空间导数方法:说实话,我之前一直很想用伪谱法,但是因为本科期间没有学过复数和傅里叶变换等,所以一直不敢动手做,今天有这个机会,那就得好好学一学。
谱方法是有限差分法的一个有用的替代方法,仍然使用伯格斯方程进行讲解:首先考虑空间域 被映射到频率域
被映射到频率域 上的一个特殊情况,假设
上的一个特殊情况,假设 的x具有
的x具有 周期,如果用
周期,如果用 来表示
来表示
相对于x的傅里叶变换,因为: 的傅里叶变换是
的傅里叶变换是 ,那么通过傅里叶变换,可以恢复
,那么通过傅里叶变换,可以恢复 的空间导数,所以,对于伯格斯方程,需要一个傅里叶变换和两个傅里叶逆变换来恢复等式右侧的两个导数,需要把其变成一个光谱算法:
的空间导数,所以,对于伯格斯方程,需要一个傅里叶变换和两个傅里叶逆变换来恢复等式右侧的两个导数,需要把其变成一个光谱算法:
假设在区间 的n个等距点上用函数值表示每一个t时刻的
的n个等距点上用函数值表示每一个t时刻的 ,那么就可以构造离散傅里叶变换(DFT),其广义上是
,那么就可以构造离散傅里叶变换(DFT),其广义上是 的傅里叶级数展开的前N项,为每个项乘以适当的乘数,然后计算逆dft。
的傅里叶级数展开的前N项,为每个项乘以适当的乘数,然后计算逆dft。
如果我们知道 是平滑的,也就是说,存在任意多个x导数并且有界,那么对于任意大的k,DFT的截断误差是
是平滑的,也就是说,存在任意多个x导数并且有界,那么对于任意大的k,DFT的截断误差是 ,如果
,如果 ,就大致可以返回
,就大致可以返回 阶的误差,有限差分法的则需要N~
阶的误差,有限差分法的则需要N~
来达到同样的精度,如果N只有小的素数因子,比如说 ,那么DFT以及其逆变换可以采用快速傅里叶变换FFT来计算,需要
,那么DFT以及其逆变换可以采用快速傅里叶变换FFT来计算,需要 次的运算,关键是,
次的运算,关键是, 既是周期性的,也是平滑性的,如果
既是周期性的,也是平滑性的,如果
 ,那么周期延拓将会是不连续的,并且吉布斯现象将破坏所有这些估计的精确性。
,那么周期延拓将会是不连续的,并且吉布斯现象将破坏所有这些估计的精确性。
scipy中有一个非常有用的函数diff,如果输入的是一个numpy数组,表示在 上均匀间隔的
上均匀间隔的 值,则函数返回一个与u形状相同的数组,包含相同x值的order阶导数的值。
值,则函数返回一个与u形状相同的数组,包含相同x值的order阶导数的值。
看一个书上给的例子: 计算导数值
计算导数值
import numpy as np
from scipy.fftpack import diffdef fd(u):"返回2*dx有限差分"ud=np.empty_like(u)ud[1:-1]=u[2:]-u[:-2]ud[0]=u[1]-u[-1]ud[-1]=u[0]-u[-2]return ud
for N in [4,8,16,32,64,128,256]:dx=2.0*np.pi/Nx=np.linspace(0,2.0*np.pi,N,endpoint= False)u=np.exp(np.sin(x))du_ex=np.cos(x)*udu_sp=diff(u)du_fd=fd(u)/(2.0*dx)err_sp=np.max(np.abs(du_sp-du_ex))err_fg=np.max(np.abs(du_fd-du_ex))print("N=%d,err_sp=%.4e,err_sp=%.4e"% (N,err_fg,err_sp))
图1
从图一可以看出,点数每增加一倍,有限差分法的误差的无限范数(最大绝对值)就减少大约4倍,光谱误差岁每个加倍呈现平方的增大,直到N非常大,N>30,这种快速的误差减小方式通常被称作指数收敛。
我们再来看一个空间周期问题的IVP:
考虑线性对流:
其精确解是
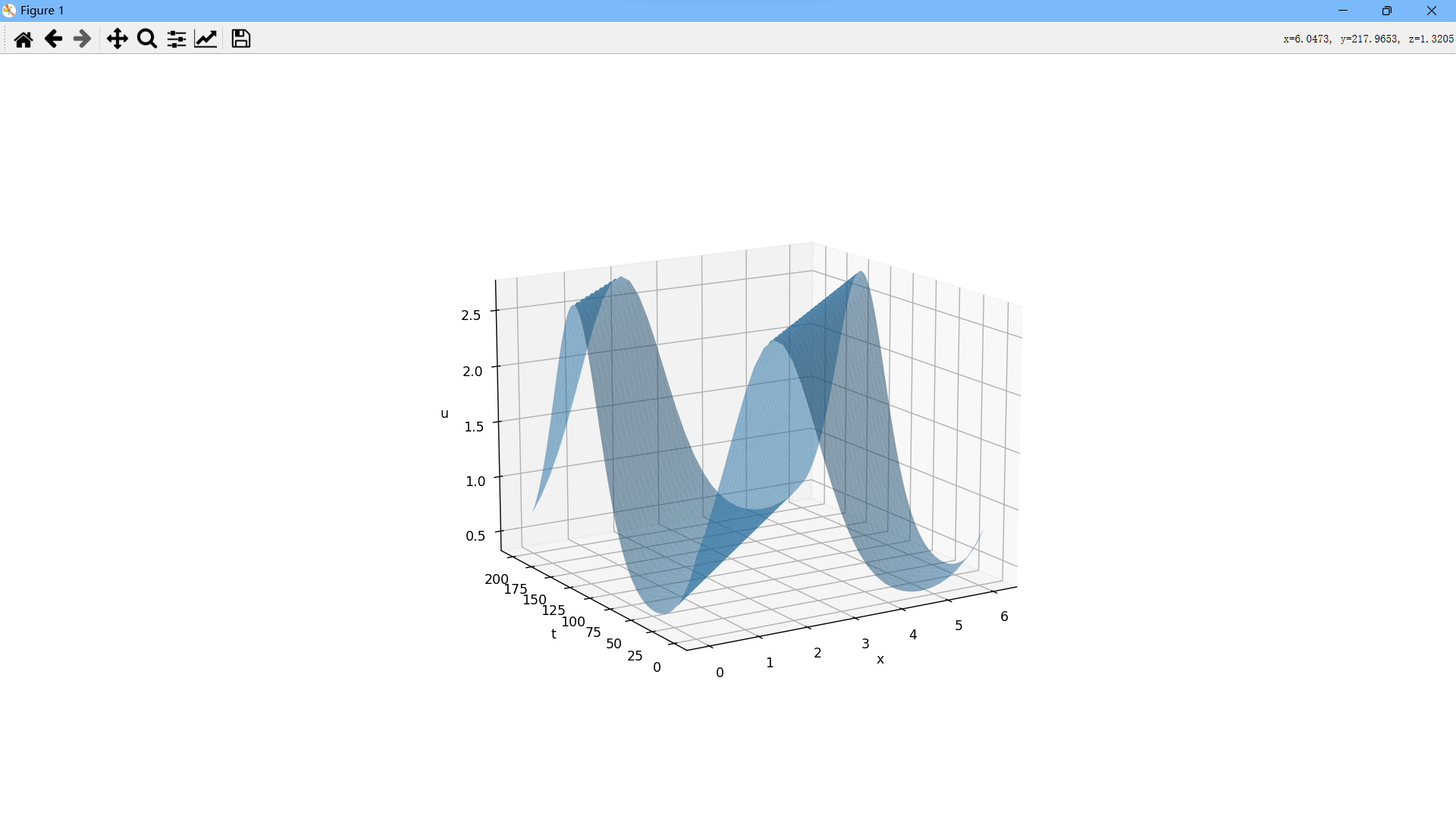
图2
结果图形说明了伪谱法的优点:即使是较粗糙的网格间距也能够产生平滑的结果。
import numpy as np
from scipy.fftpack import diff
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#6-19建立问题
def u_exact(t,x):"Exact solution"return np.exp(np.sin(x-2*np.pi*t))
def rhs(u,t):"return rhs."return -2.0*np.pi*diff(u)
N=32
x=np.linspace(0,2*np.pi,N,endpoint=False)
u0=u_exact(0,x)
t_initial=0.0
t_final=64*np.pi
t=np.linspace(t_initial,t_final,101)
#20行用来求解
sol=odeint(rhs,u0,t,mxstep=5000)
#可视化
fig=plt.figure()
ax=fig.add_subplot(1,1,1, projection='3d')
t_gr,x_gr=np.meshgrid(x,t)
ax.plot_surface(t_gr,x_gr,sol,alpha=0.5)
ax.elve,ax.azim=47,-137
ax.set_xlabel("x")
ax.set_ylabel("t")
ax.set_zlabel("u")
plt.show()
u_ex=u_exact(t[-1],x)
err=np.abs(np.max(sol[-1,:]-u_ex))
print("with %d fourier nodes the final error = %g"%(N,err))再,再看看,理解理解。
相关文章:

Python科学计算:偏微分方程1
首先,我们来看初边值问题:伯格斯方程:假设函数是定义在上的函数,且满足:右侧第一项表示自对流,第二项则表示扩散,在许多物理过程中,这两种效应占据着主导地位,为了固定一…...
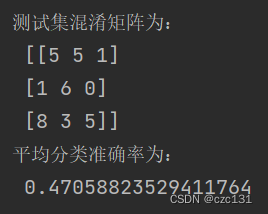
PLS-DA分类的实现(基于sklearn)
目录 简单介绍 代码实现 数据集划分 选择因子个数 模型训练并分类 调用函数 简单介绍 (此处取自各处资料) PLS-DA既可以用来分类,也可以用来降维,与PCA不同的是,PCA是无监督的,PLS-DA是有监督的…...
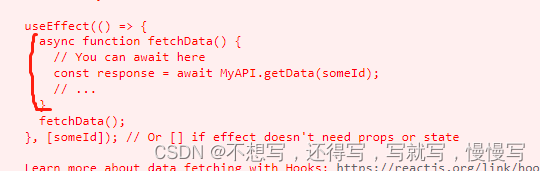
常用hook
Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。理解:hook是react提供的函数API官方提供的hook基础hookuseState APIconst [state, setState] useState(initialState); //返回state值 以及更新state的方法 …...
TryHackMe-GoldenEye(boot2root)
GoldenEye 这个房间将是一个有指导的挑战,以破解詹姆斯邦德风格的盒子并获得根。 端口扫描 循例nmap Web枚举 进入80 查看terminal.js 拿去cyberchef解码 拿着这组凭据到/sev-home登录 高清星际大战 POP3枚举 使用刚刚的凭据尝试登录pop3 使用hydra尝试爆破 这…...
Elasticsearch基本安全加上安全的 HTTPS 流量
基本安全加上安全的 HTTPS 流量 在生产环境中,除非您在 HTTP 层启用 TLS,否则某些 Elasticsearch 功能(例如令牌和 API 密钥)将被禁用。这个额外的安全层确保进出集群的所有通信都是安全的。 当您在模式下运行该elasticsearch-ce…...
C语言-程序环境和预处理(2)
文章目录预处理详解1.预定义符号2.#define2.1#define定义的标识符2.2#define定义宏2.3#define替换规则注意事项:2.4#和###的作用##的作用2.5带副作用的宏参数2.6宏和函数的对比宏的优势:宏的劣势:宏和函数的一个对比命名约定3.undef4.条件编译…...
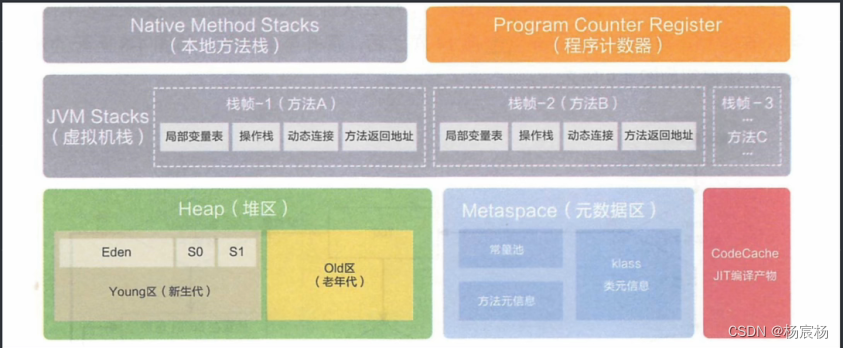
JVM 收集算法 垃圾收集器 元空间 引用
文章目录JVM 收集算法标记-清除算法标记-复制算法标记-整理算法JVM垃圾收集器Serial收集器ParNew收集器Parallel Scavenge /Parallel Old收集器CMS收集器Garbage First(G1)收集器元空间引用强引用软引用弱引用虚引用JVM 收集算法 前面我们了解了整个堆内存实际是以分代收集机制…...
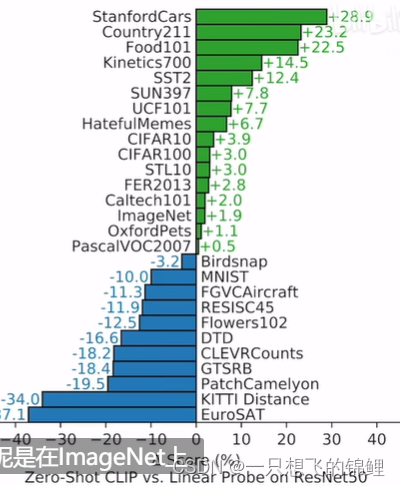
clip精读
开头部分 1. 要点一 从文章题目来看-目的是:使用文本监督得到一个可以迁移的 视觉系统 2.要点二 之前是 fix-ed 的class 有诸多局限性,所以现在用大量不是精细标注的数据来学将更好,利用的语言多样性。——这个方法在 nlp其实广泛的存在&…...
vue 首次加载慢优化
目前使用的是vue2版本 1.路由懒加载(实现按需加载) component: resolve > require([/views/physicalDetail/index], resolve)2.gzip压缩插件(需要运维nginx配合) 第一步,下载compression-webpack-plugin cnpm i c…...

WuThreat身份安全云-TVD每日漏洞情报-2023-03-21
漏洞名称:CairoSVG 文件服务器端请求伪造 漏洞级别:严重 漏洞编号:CVE-2023-27586 相关涉及:CairoSVG 在 2.7.0 版本之前 漏洞状态:POC 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-06718 漏洞名称:WP Meta SEO WordPress 授权不当导致任意重定向 漏洞级…...
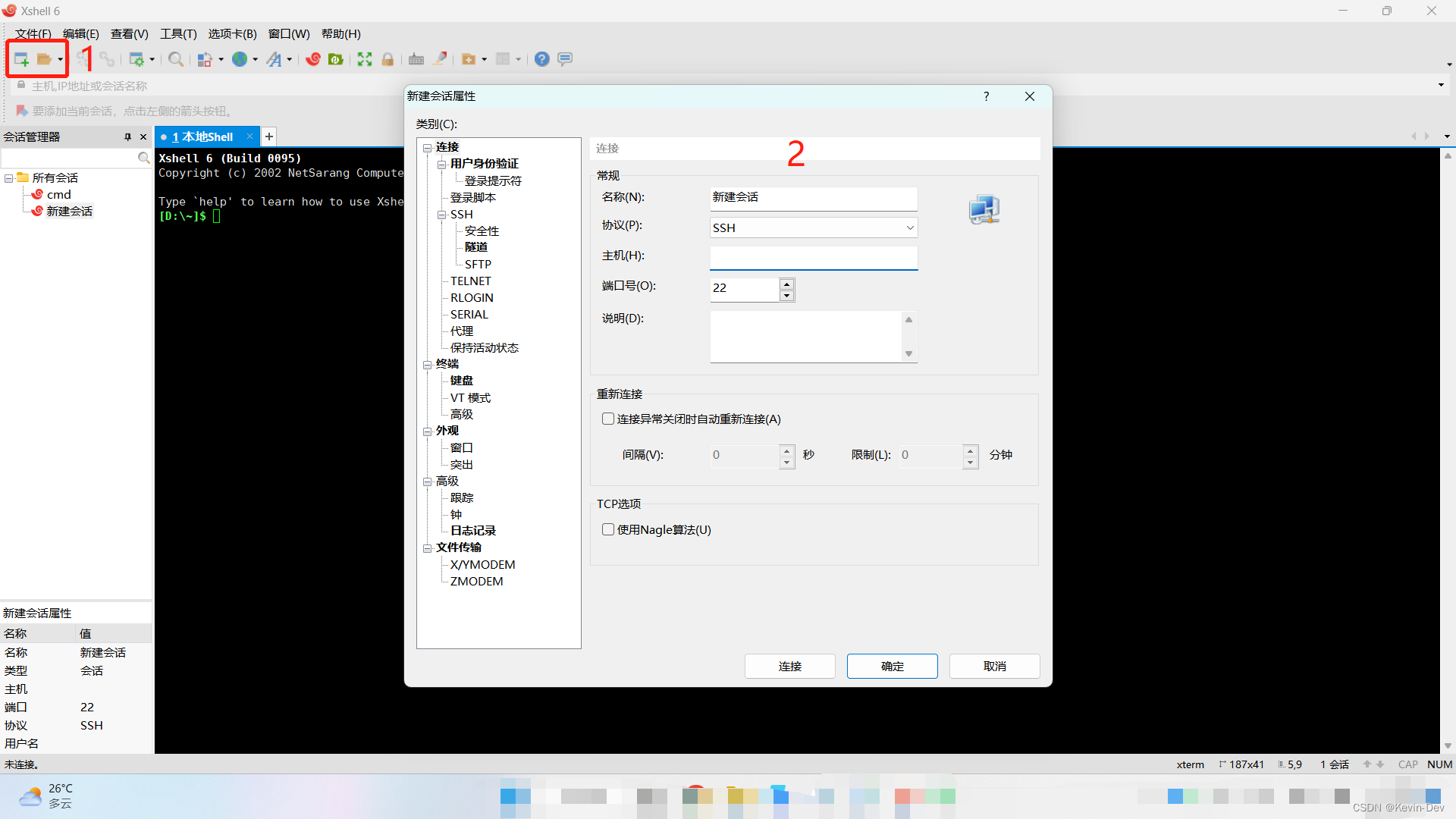
【Android -- 开发工具】Xshell 6 安装和使用教程
一、简介 Xshell 其实就是一个远程终端工具,它可以将你的个人电脑和你在远端的机器连接起来,通过向 Xshell 输入命令然后他通过网络将命令传送给远端Linux机器然后远端的Linux机器将其运行结果通过网络传回个人电脑。 二、Xshell 6 的安装 首先&#…...

国民技术RTC备份寄存器RTC_BKP
根据手册资料知道RTC_BKP的地址,代码如下 #include "main.h" #include "usart.h"void USART2_Configuration(void) {USART_InitType USART_InitStructure;GPIO_InitType GPIO_InitStructure;GPIO_InitStruct(&GPIO_InitStructure);RCC_Ena…...
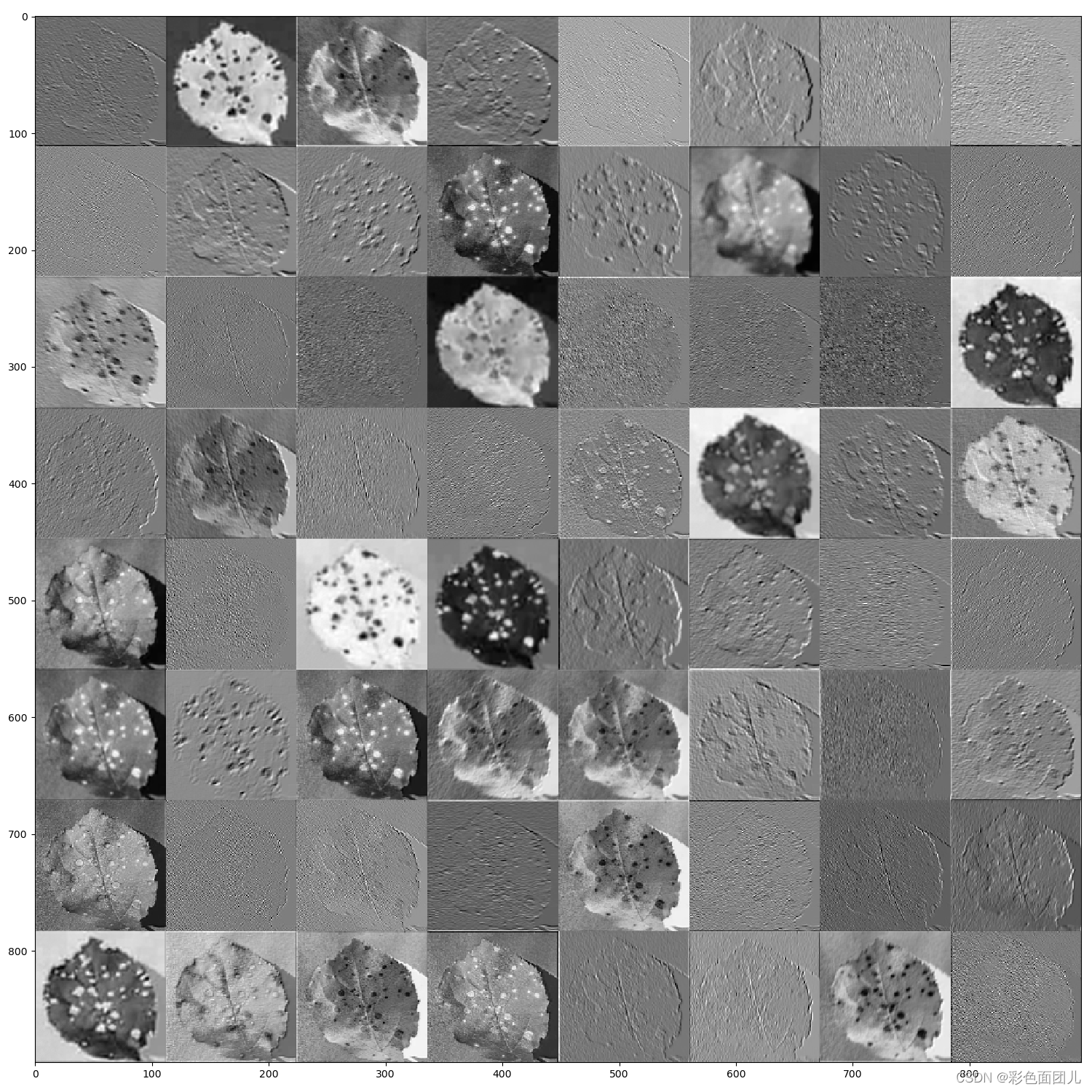
resnet网络特征提取过程可视化
我们在训练图片时,是不是要看看具体提取时的每个特征图提取的样子,找了很多,终于功夫不负有心人,找到了,通过修改的代码: resnet代码: import torch import torch.nn as nn from torchvision…...
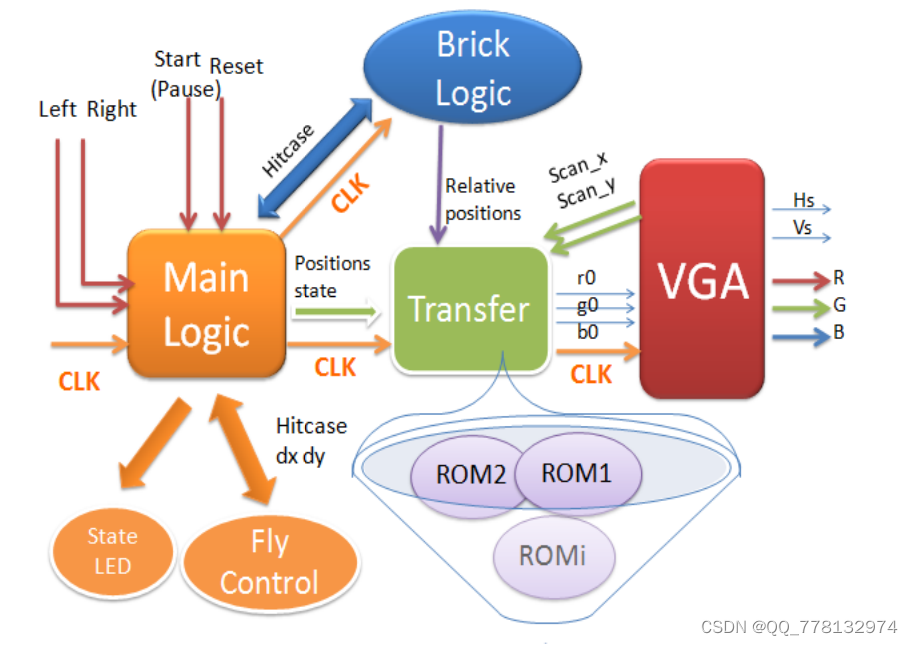
FPGA打砖块游戏设计(有上板照片)VHDL
这是一款经典打砖块游戏,我们的努力让它更精致更好玩,我们将它取名为打砖块游戏(Flyball),以下是该系统的一些基本功能: 画面简约而经典,色彩绚丽而活泼,动画流畅 玩家顺序挑战3个不同难度的级别,趣味十足 计分功能,卡通字母数字 4条生命值,由生命条显示…...

【Unity入门】3D物体
【Unity入门】3D物体 大家好,我是Lampard~~ 欢迎来到Unity入门系列博客,所学知识来自B站阿发老师~感谢 (一)物体移动旋转缩放 (1)物体移动 在上一篇文章【Unity入门】场景视图操作我们学会了在场景中创建3…...
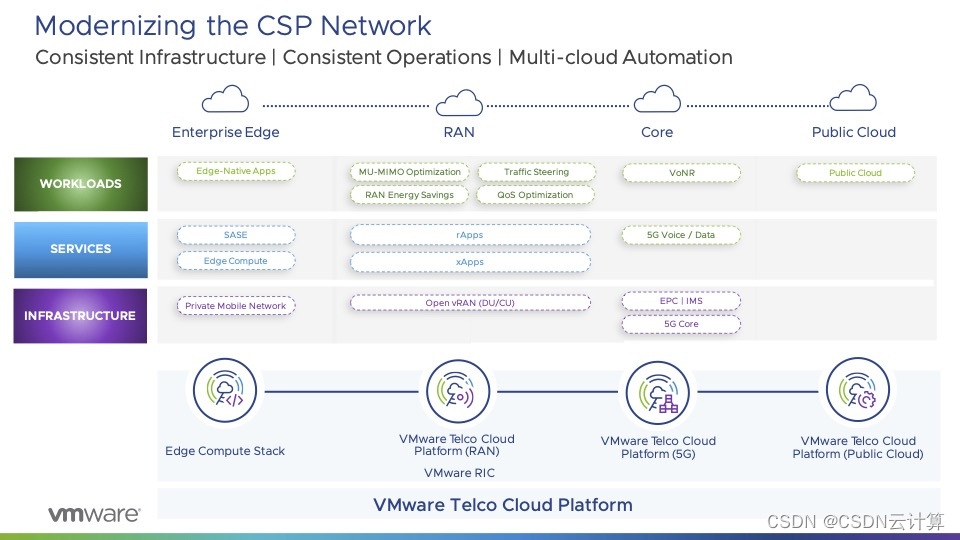
网络现代化势在必行,VMware 发布软件定义网络 SD-WAN 全新方案
出品 | CSDN云计算 作为计算存储网络基础设施三大件之一,网络一直是 IT 核心技术,并不断向前发展。 数字化转型浪潮下,各行业都在探索创新应用,而数字化创新,也是对 5G 和云边端等网络基础设施提出更高需求,…...

java学习笔记——抽象类
2.1 概述 由来 父类中的方法,被他的子类们重写,子类各自的实现都不尽相同。那么父类的方法声明和方法主体,只有声明还有意义,而方法主体则没有存在的意义了。我们把没有主体的方法称为抽象方法。java语法规定,包含抽象…...

Redis删除策略
删除策略就是针对已过期数据的处理策略。 针对过期数据要进行删除的时候都有哪些删除策略呢? 1.定时删除2.惰性删除3.定期删除1、立即删除 当key设置有过期时间,且过期时间到达时,由定时器任务立即执行对键的删除操作。 优点:节…...

【新星计划2023】SQL SERVER (01) -- 基础知识
【新星计划2023】SQL SERVER -- 基础知识1. Introduction1.1 Official Website1.2 Conn Tool2. 基础命令2.1 建库建表2.2 Alter2.3 Drop2.3 Big Data -- Postgres3.Awakening1. Introduction 1.1 Official Website 官方文档(小技巧) Officail Website: …...
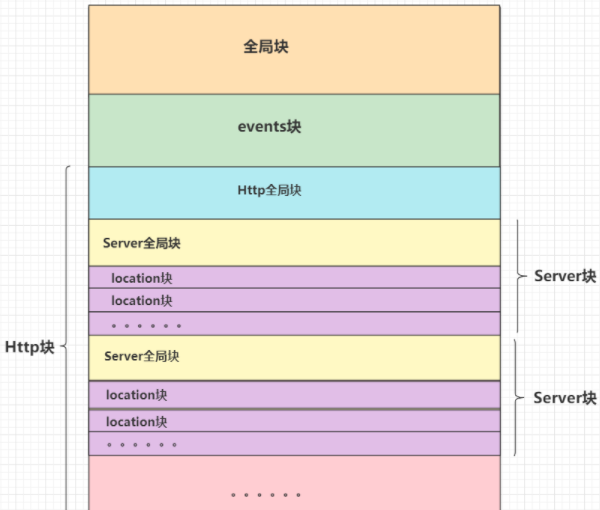
nginx配置详解
一.nginx常用命令1.Windows(1).查看nginx的版本号nginx -v(2).启动nginxstart nginx(3).快速停止或关闭nginxnginx -s stop(4).正常停止或关闭nginxnginx -s quit(5).配置文件nginx.conf修改重装载命令nginx -s reload2.Linux(1).进入 nginx 目录中cd /usr/local/nginx/sbin(2)…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
