24/8/12算法笔记 复习_线性回归
import numpy as np#导入包
X = np.array([[1,1],[2,1]])#构造矩阵
y = np.array([14,10])np.linalg.solve(X,y) #linalg是线性代数,用于求解线性方程AX = b,solve计算线性代数回归问题X.T#转置
a = X.T.dot(X)#矩阵乘法B = np.linalg.inv(a)#求逆矩阵from sklearn.linear_model import LinearRegression #导入线性回归代数model = LinearRegression(fit_intercept=False) #不计算斜率,没有使用正规方程model.fit(X,y)#用于训练模型model.coef_ #结果,返回值:系数,斜率
model.intercept_ #表示截距项y = y+12 #带截距的线性方程X = np.array([[1,2],[3,4]]) #假设X是一个numpy数组ones_array = np.full((X.shape[0],1),fill_value = 1)#使用np.full创建形状匹配X的数组X = np.concatenate([X,ones_array],axis = 1)#使用np.concatenate在X的每行末尾添加ones_array#线性回归中的截距项:在进行线性回归时,通常需要在特征矩阵中添加一个全为1的列,以便模型可以学习截距项。这样,模型就可以估计出在所有特征值为0时的预测值。#正规方程计算
import matplotlib.pyplot as plt
import numpy as npX = np.linspace(0,10,num = 30).reshape(-1,1) #生成一个数组,以矩阵方式存在,reshape(-1,1) 确保了数据以矩阵的形式存在,便于进行矩阵运算。#斜率和截距随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)#方程
y = X*w+b+np.random.randn(30,1) #X是特征矩阵,w是权重向量,b是偏置项,np.random是添加的随机噪声plt.scatter(X,y) #绘制散点图
注意点 :
为什么要添加one_array
在机器学习和统计建模中,添加一个全为1的数组(通常称为“ones array”)到数据集中有几种常见原因:
-
线性回归中的截距项:在进行线性回归时,通常需要在特征矩阵中添加一个全为1的列,以便模型可以学习截距项。这样,模型就可以估计出在所有特征值为0时的预测值。
-
逻辑回归:在逻辑回归中,添加一个全为1的列允许模型包含一个常数项,这对于某些类型的数据是必要的。
-
特征标准化:在特征标准化过程中,添加一个全为1的列可以保持数据的维度不变,同时允许模型在标准化过程中考虑所有特征。
-
神经网络输入:在构建神经网络时,添加一个全为1的列可以作为偏置项(bias),类似于在每个神经元中添加一个偏置参数。
-
稀疏矩阵优化:在处理稀疏矩阵时,添加一个全为1的列可以简化某些操作,例如在某些优化算法中。
-
数据预处理:在某些数据预处理步骤中,添加一个全为1的列可以帮助实现特定的数据处理或特征工程需求。
-
模型泛化:在某些情况下,添加全为1的列可以帮助模型更好地泛化,特别是在数据集中某些特征的值可能为0时。
reshape的用处:reshape(-1,1) 确保了数据以矩阵的形式存在,便于进行矩阵运算。
y = X*w+b+np.random(30,1) 的理解:X 是特征矩阵,w 是权重向量,b 是偏置项,而 np.random(30,1) 是添加的随机噪声。
randn,和randint函数区别:
-
randn:
np.random.randn(*size)函数用于生成标准正态分布(均值为0,标准差为1)的随机样本。这里的size可以是一个或多个整数,指定了输出数组的形状。- 例如,
np.random.randn(3, 2)会生成一个3行2列的数组,数组中的每个元素都是从标准正态分布中抽取的。
-
randint:
np.random.randint(low, high=None, size=None, dtype=int)函数用于生成随机整数。low和high是整数,分别表示随机数的最小值和最大值(不包括high)。size参数指定了输出数组的形状。dtype参数指定了输出数组的数据类型,默认是整数类型。- 例如,
np.random.randint(1, 10, size=(3, 2))会生成一个3行2列的数组,数组中的每个元素都是从1到9之间的随机整数。
相关文章:

24/8/12算法笔记 复习_线性回归
import numpy as np#导入包 X np.array([[1,1],[2,1]])#构造矩阵 y np.array([14,10])np.linalg.solve(X,y) #linalg是线性代数,用于求解线性方程AX b,solve计算线性代数回归问题X.T#转置 a X.T.dot(X)#矩阵乘法B np.linalg.inv(a)#求逆矩阵from sklearn.linea…...

Linux系统驱动(十四)输入子系统
文章目录 一、输入子系统(一)输入子系统框架结构(二)输入子系统的API 二、实现两个按键的驱动(一)实现思路(二)代码实现 一、输入子系统 在linux系统中使用输入子系统驱动上报鼠标&…...
)
力扣(2024.08.12)
1. 98:验证二叉搜索树 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.right right class Solution:def isValidBST(self, r…...
最新版的AutoGPT,我搭建好了
最近AutoGPT不是更新了嘛 安装 我按照官方的教程 在本地搭建好了 改动 可见的改动,主要是把原来的纯命令行改成前后端的形式 看下前端界面 界面比较简单,主要分3个大块 监控 第一个是监控 主要是看你在 build 里构建的Agents的运行情况 build 第一个是Ag…...

[SWPUCTF 2021 新生赛]PseudoProtocols(构造伪协议)
打开题目所给的环境我们可以看到这样一句话: 这里我先尝试访问/hint.php ,但是发现什么都没有发生, F12查看源代码也并没有发现什么,到这里来看的话似乎没有思路了,但是这个题的题目已经给了我们很明显的提示ÿ…...

基于STM32开发的智能语音助手系统
目录 引言环境准备工作 硬件准备软件安装与配置系统设计 系统架构硬件连接代码实现 初始化代码控制代码应用场景 智能家居控制个人语音助理常见问题及解决方案 常见问题解决方案结论 1. 引言 随着人工智能技术的发展,智能语音助手已经逐渐进入了人们的日常生活。…...

基于python的图像去雾算法研究系统设计与实现
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...

自定义 View 可以播放一段视频
请实现一个自定义 View 的核心代码,核心要求可以响应如下事件: // - 要求自定义 View 可以播放一段视频 / - 在 view 左侧区域上下滑动,可以提高减少音量 / / - 在 view 右侧区域上下滑动可以提高减少屏幕亮度 // - 在 view 左右滑动可以…...
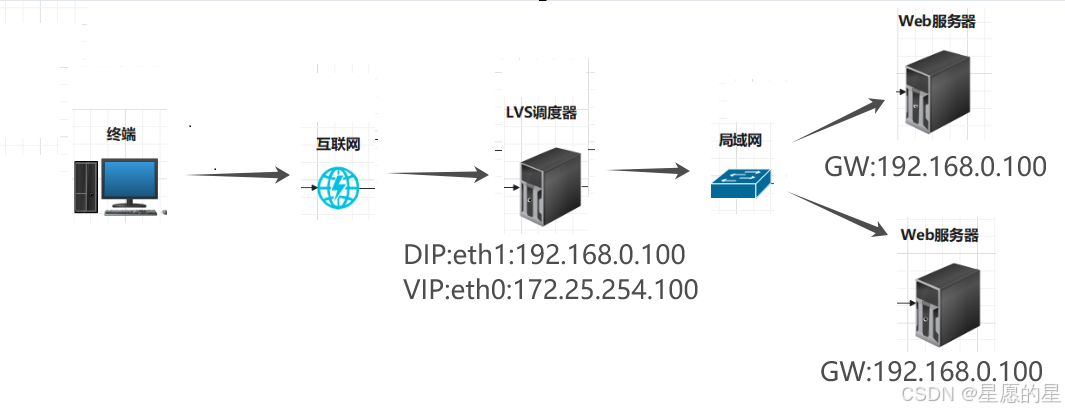
LVS负载均衡集群部署之—NAT模式的介绍及搭建步骤
一、环境准备 1.准备三台rhel9服务器 服务器名称 主机名 ip地址备注LVS调度服务器lvs.timinglee.org eth0:172.25.254.100(外网) eth1:192.168.0.100(内网) 关闭selinux和防火墙webserver2网站服务器webserver1.timinglee.orgeth0:192.168.…...

【算法】浅析哈希算法【附代码示例】
哈希算法:数据存储与检索的基石 1. 引言 在计算机科学中,哈希算法是一种用于将数据(如文件、网络地址或数据库记录)转换为固定长度的哈希值的过程。哈希值通常是一个较短的数字或字符串,用于快速检索原始数据或验证数…...
2024.8.12
2024.8.12 【梦最让我费解的地方在于,明明你看不清梦里人们的脸,却清晰地知道他们是谁。】 Monday 七月初九 序理论 最小链覆盖&最长反链长度 我们设定一个二元关系符R和一个集合A 我们设定<A,R>这样一个类群,那么对于任意 a i…...

使用Python解析pdf、docx等格式文件。
针对不同类型的文件,需要采取特定的访问与解析策略来有效获取其中蕴含的知识。下面我们将介绍对于不同数据源数据的获取方式。 1 解析Docx文档 1.1 获取Docx文档中文本 from docx import Document # pip install python-docx # python-docx 0.8.11 filename xx…...

Linux网络通信基础API
这篇文章只有Linux网络通信基础API大参数信息,和返回值,这篇文章并没有这些基础API的参数类型介绍。accept的第二个参数可以查看客户端信息。 创建socket #include <sys/types.h> /* See NOTES */#include <sys/socket.h>int sock…...

Python爬虫:下载4K壁纸
🎁🎁创作不易,关注作者不迷路🎀🎀 目录 🌸完整代码 🌸分析 🎁基本思路 🎁需要的库 🎁提取图片的链接和标题 👓寻找Cookie和User-Agent &…...

2024年【北京市安全员-B证】新版试题及北京市安全员-B证免费试题
题库来源:安全生产模拟考试一点通公众号小程序 2024年【北京市安全员-B证】新版试题及北京市安全员-B证免费试题,包含北京市安全员-B证新版试题答案和解析及北京市安全员-B证免费试题练习。安全生产模拟考试一点通结合国家北京市安全员-B证考试最新大纲…...

python爬取B站视频实验
实验17:爬虫2 文章目录 实验17:爬虫21.实验目标及要求2. 实验主要内容3.实验小结 1.实验目标及要求 (1)掌握有关爬虫的包 (2)掌握爬虫方法 (3)爬取B站卡塔尔世界杯若干视频 2. 实验…...

10步搞定Python爬虫从零到精通!
学习Python网络爬虫可以分为以下几个步骤,每一步都包括必要的细节和示例代码,以帮助你从零开始掌握这一技能。 第一步:理解网络爬虫基础 什么是网络爬虫? 网络爬虫是一种自动化程序,用来从互联网上收集数据.它通过发送 HTTP 请求…...

SpringMVC学习笔记---带你快速入门和复习
一、初识SpringMVC 1.1、什么是SpringMVC 1.1.1、什么是MVC MVC是一种软件架构模式(是一种软件架构设计思想,不止Java开发中用到,其它语言也需要用到),它将应用分为三块: M:Model࿰…...

Linux系统编程 day09 线程同步
Linux系统编程 day09 线程同步 1.互斥锁2.死锁3.读写锁4.条件变量(生产者消费者模型)5.信号量 1.互斥锁 互斥锁是一种同步机制,用于控制多个线程对共享资源的访问,确保在同一时间只有一个线程可以访问特定的资源或执行特定的操作…...

Vue快速入门(四)——Vue3及组合式API(一)
文章目录 一、认识Vue31. Vue2 选项式 API vs Vue3 组合式API2. Vue3的优势二、使用create-vue搭建Vue3项目1、认识create-vue2. 使用create-vue创建项目三、组合式API - setup选项1. setup选项的写法和执行时机2. setup中写代码的特点3. `<script setup>`语法糖4.小结四…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
