算法板子:线性DP——算出三角形中的最大路径值、求最长上升子序列、求最长公共子序列
目录
一、数字三角形——算出三角形中的最大路径值
二、最长上升子序列——求一个数组中的最长递增子序列
三、最长公共子序列——求两个字符串中的最长公共子序列
一、数字三角形——算出三角形中的最大路径值
#include <iostream>
using namespace std;const int N = 500 + 10;
int a[N][N];int main()
{int n;cin >> n;// 存储三角形for (int i = 0; i < n; i ++ )for (int j = 0; j <= i; j ++ )cin >> a[i][j];// 从三角形的倒二行开始倒着遍历; 对于每一行的每一个元素,将该元素左下角和右下角中更大的元素加在其本身上; 比如倒二行的第一个元素,4和5中5更大,加在2上变成7.for (int i = n - 2; i >= 0; i -- )for (int j = 0; j <= i; j ++ )a[i][j] = max(a[i + 1][j], a[i + 1][j + 1]) + a[i][j];// 三角形中最大路径值存在(0,0)位置cout << a[0][0] << endl;return 0;
}二、最长上升子序列——求一个数组中的最长递增子序列
#include <iostream>
using namespace std;const int N = 1000 + 10;// a数组存储题目中给定的数组
// f[i]代表以i指针所指元素结尾的上升子序列的长度; f[4]=3代表以下标4元素结尾的子序列的长度为3
int a[N], f[N];int main()
{int n;cin >> n;for (int i = 0; i < n; i ++ ) cin >> a[i];// 初始化最长上升子序列的长度为1int ans = 1;// 初始化f数组元素全为1for (int i = 0; i < n; i ++ ) f[i] = 1;// 指针i从下标1开始遍历数组for (int i = 1; i < n; i ++ ){// 指针j从下标0遍历到指针i之前for (int j = 0; j < i; j ++ )// 如果发现j所指元素小于i所指元素,那么可以构成上升子序列,更新f[i]if (a[j] < a[i]) f[i] = max(f[j] + 1, f[i]);ans = max(ans, f[i]);}cout << ans << endl;return 0;
}三、最长公共子序列——求两个字符串中的最长公共子序列
#include <iostream>
using namespace std;const int N = 1000 + 10;// f[i][j]中的指针i指向s1,指针j指向s2,f[i][j]代表s1中指针i之前的部分和s2中指针j之前的部分的最长公共子序列的长度; f[7][9]=3代表s1中的前7个字符和s2中的前9个字符的最长公共子序列的长度为3
int f[N][N];
int n, m;
string s1, s2;int main()
{cin >> n >> m >> s1 >> s2;for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )// 如果s1的i-1位等于s2的j-1位,那么这一位可以并入s1的前i位和s2的前j位的公共子序列中,更新前i位和前j位的最长公共子序列的长度if (s1[i - 1] == s2[j - 1]) f[i][j] = f[i - 1][j - 1] + 1;// 如果不相等,一个是i-1一个是j-1求maxelse f[i][j] = max(f[i - 1][j], f[i][j - 1]);cout << f[n][m] << endl;return 0;
}相关文章:

算法板子:线性DP——算出三角形中的最大路径值、求最长上升子序列、求最长公共子序列
目录 一、数字三角形——算出三角形中的最大路径值 二、最长上升子序列——求一个数组中的最长递增子序列 三、最长公共子序列——求两个字符串中的最长公共子序列 一、数字三角形——算出三角形中的最大路径值 #include <iostream> using namespace std;const int N …...

【C++】值传递
函数值传递的特点:值传递过程中即使形参改变也不会改变实参 没有返回值的函数用“ void ”定义 下面是一个实例: #include<iostream> using namespace std;//值传递 //定义函数,实现两个数字进行交换函数//如果函数不需要返回值&…...

工业三防平板助力MES系统打造工厂移动式生产管理
随着工业4.0时代的到来,智能制造、数字化车间等概念层出不穷,生产过程的可视化管理也成为了企业提升效率、优化生产的关键。而工业三防平板,凭借其坚固耐用、功能强大、便携易用等特性,成为了实现生产过程可视化管理的重要利器&am…...

keepalived+nginx实现的简单高可用故障转移
keepalived和nginx和适配 nginx服务停止后对keepalived的影响最近研究了一下keepalived绑定虚拟Ip,然后实现集群的方案,发现实现故障转移的模式,只有在keepalived服务整个挂掉后才能实现虚拟IP的漂移,和实际应用的场景不怎么适配,所以把它和nginx结合在一起实现集群高可用…...

openai api使用
1OpenAI 的 API 介绍 1.1 api分类 常用的 OpenAI Api 接口总共分为 4 类:对话类、私有化模型训练类、通用类、图片 & 音频类,其中对话类与私有化模型训练类是最常用的。 a .对话类 这类是最常用也是最核心的接口,用于人机对话。对话类…...

带你走进haproxy的世界
华子目录 前言什么是负载均衡为什么用haproxy负载均衡负载均衡公司负载均衡类型四层负载均衡七层负载均衡四层和七层的区别 haproxy介绍haproxy的安装与服务信息软件安装haproxy基本配置信息proxies配置socat工具 haproxy算法静态算法动态算法其他算法 高级功能及配置基于cooki…...
)
STM32--中断使用(超详细!)
STM32中断机制是嵌入式系统设计中一个非常重要的组成部分,它允许单片机在执行程序的过程中,对外部或内部发生的事件做出快速响应。以下是一篇关于STM32中断机制的详细介绍和示例代码,希望能够帮助你更好地理解和应用中断。 一、中断的基本概…...

【深度学习实践】基于深度学习的图像去雾算法-ChaIR-实践
本文介绍一个去雾算法ChaIR的使用方法,可以完成图像去雾,也可以用于图像去雨、去噪音等任务。本文不涉及论文原理,只包含源代码的跑通和使用。 先展示一下效果: 原图去雾 论文:Exploring the potential of channel …...
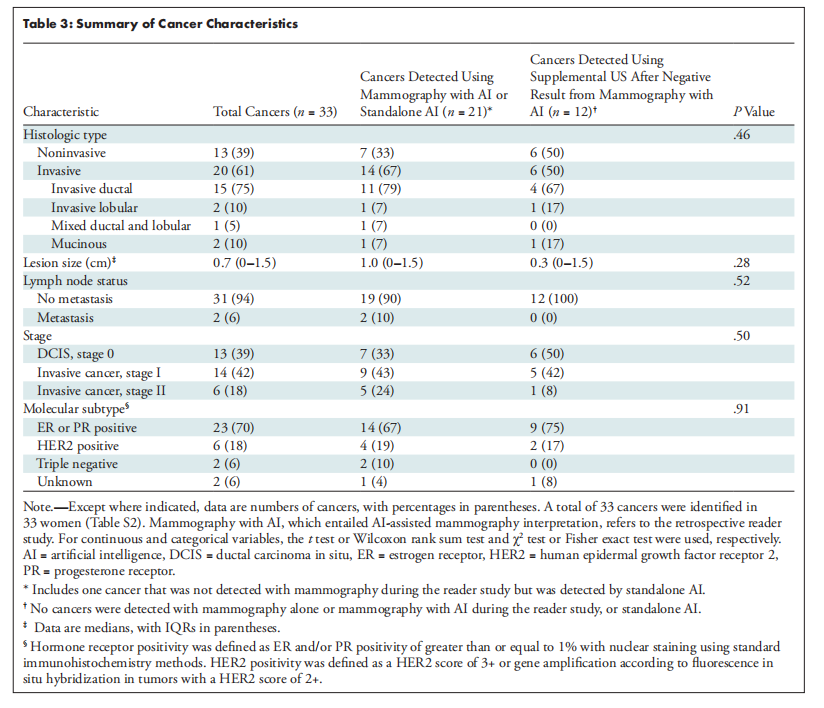
《乳腺密度高的女性中,使用AI辅助的乳腺X线筛查与补充筛查超声的比较研究》| 文献速递-基于深度学习的乳房、前列腺疾病诊断系统
Title 题目 Screening Outcomes of Mammography with AI in Dense Breasts: A Comparative Study with Supplemental Screening US 《乳腺密度高的女性中,使用AI辅助的乳腺X线筛查与补充筛查超声的比较研究》 Background 背景 Comparative performance between…...

crm 销售管理系统有哪些?国内外排名前十盘点
本文深入对比的 crm销售管理系统有:1.纷享销客; 2.Zoho CRM; 3.销售易; 4.有赞CRM; 5.Salesforce; 6.HubSpot; 7.简道云CRM; 8.爱客CRM; 9.Apptivo。 如果你正寻找一种方…...

package-lock.json 要提交到git吗?
之前一直没有提交package-lock.json文件到git仓库,直到我打包失败了。。。 我才知道package-lock.json需要提交到git仓库。 npm官网建议将package-lock.json一起提交到代码库中,不要忽略它。 package-lock.json的主要作用是锁定dependencies的版…...

算法学习day32
一、解码方法II(解码方法I的升级版) 在I的基础上增加了*,可以代替1-9中任意一个数字,求解码的方法有多少种 输入:s "*" 输出:9 解释:这一条编码消息可以表示 "1"、"…...

知识与智慧
前两天在medium上看到一篇文章,探讨知识(knowledge)和智慧(wisdom)之间的区别,很受启发,结合自己的经历和理解,形成此文: 何为知识 知识通常指的是信息的积累和对特定领…...
使用FFmpeg实现摄像头RTMP实时推流
在当今的数字时代,视频直播已成为连接人与人之间的重要桥梁,广泛应用于在线教育、远程会议、娱乐直播等多个领域。随着技术的不断进步,人们对于直播的实时性、稳定性和高质量需求日益增加。为了实现高效的视频直播,选择合适的工具和协议至关重要。 RTMP(Real-Time Messagi…...
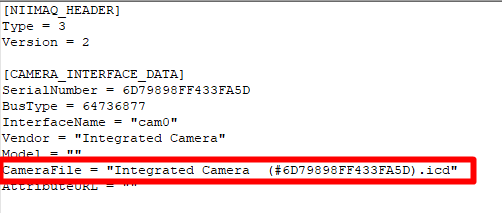
使用 LabVIEW 编程更改 IMAQ/IMAQdx 接口的相机文件
问题详情 可能需要通过编程方式更改与 IMAQ/IMAQdx 接口关联的相机文件。这种需求通常发生在图像采集系统中,例如使用 PCIe-1433 硬件时,可能需要动态切换不同的相机配置文件来适应不同的应用场景。 解决方案 当前在 Measurement & Automation Ex…...

[后端代码审计] PHP 基础学习
文章目录 前言1. 基础语法1 .1 注释1 .2 分隔符 2. 变量与常量2 .1 变量2 . 1 .1 变量定义2 . 1 .2 变量释放 2 .2 常量2 . 2 .1 常量定义2 . 2 .2 预定义常量 3. 运算符3. 1 算数运算符3 .2 字符串运算符3 .3 赋值运算符3 .4 比较运算符3 .5 逻辑运算符3 .6 其他运算符 4. 流程…...

【OpenCV C++20 学习笔记】直方图计算-split, calcHist, normalize
直方图计算-split, calcHist, normalize 广义直方图示例目标分离通道计算直方图绘制计算结果归一化绘制 最终结果 广义直方图 直方图的横坐标除了可以是图片中的强度值,也可以是任何其他我们想要观察的特征。例如,下面的图片矩阵中包含了0-255的强度值&…...

js入门经典学习小结
简介 js是解释型语言,虽然名字有java,但和java,c等编译型语言不同,它是解释型的,类似perl,py 历史 90年代最早js 1.0版本是网景navigator2引入的 然后欧洲计算机制造商协会(ECMA)…...
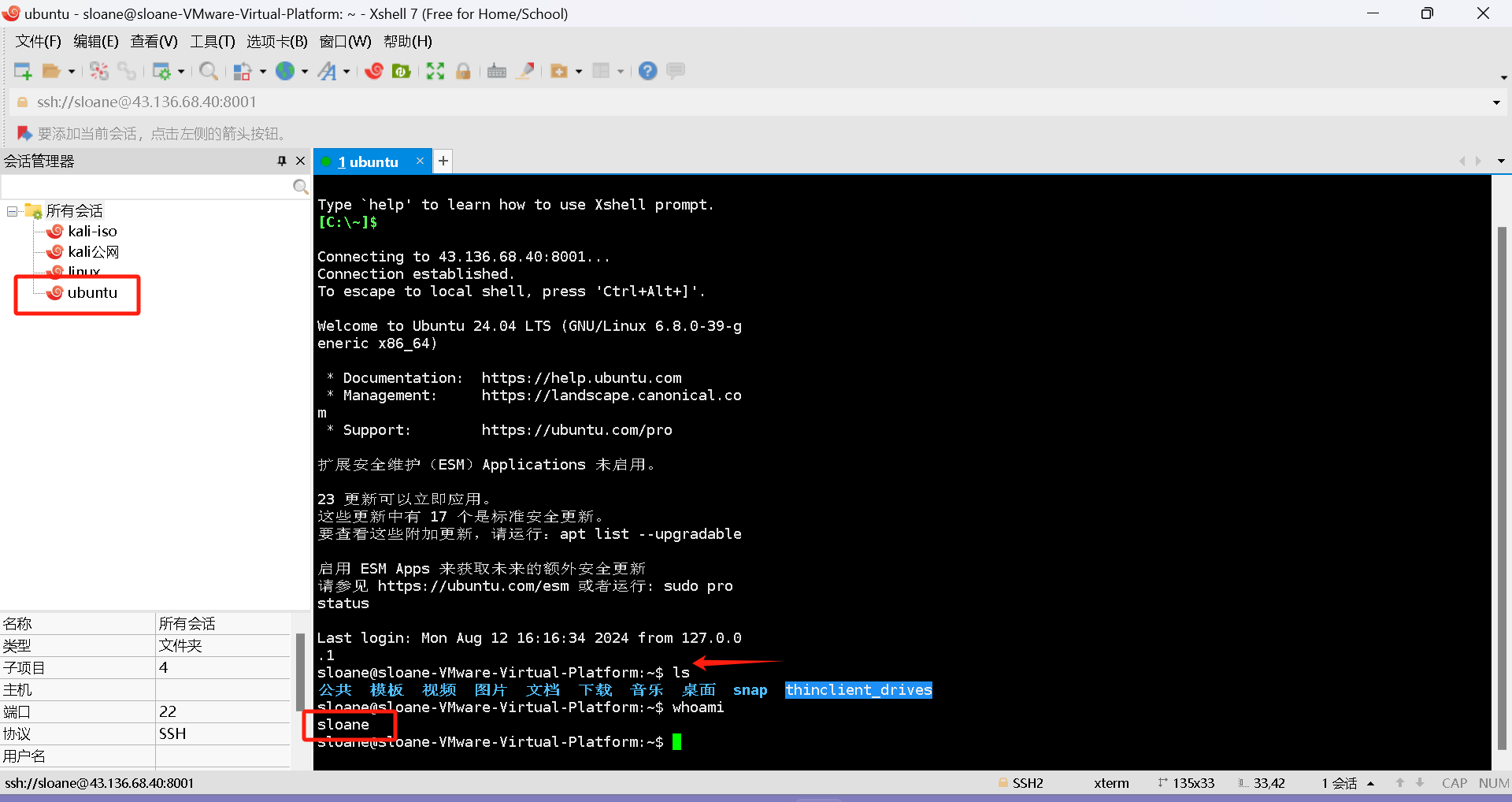
nps内网穿透之——腾讯云服务器和linux虚拟机
准备 1、客户端:准备一个内网的linux内网主机,或是一个虚拟机。 2、服务端:准备一个云服务器(阿里、腾讯、华为都行)。 安装方式: 1、自己到Github官网下载安装包上传。 下载地址:https://…...

大数据知识点
VMWare 设置网段 虚拟机设置 JDK部署 云平台 创建VPC 找到阿里云控制台里的VPC,点击专有网络 安全组 搁置…有需要再使用,因为每月要花200左右 大数据 数据导论...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
