【数据结构】排序
作者:✿✿ xxxflower. ✿✿
博客主页:xxxflower的博客
专栏:【数据结构】篇
语录:⭐每一个不曾起舞的日子,都是对生命的辜负。⭐
文章目录
- 1.排序
- 1.1排序的概念
- 1.2常见的排序算法
- 2.常见排序算法
- 2.1插入排序
- 2.1.1直接插入排序
- 2.1.2希尔排序(缩小增量排序)
- 2.2选择排序
- 2.2.1基本思想
- 2.2.3 堆排序
- 2.3交换排序
- 2.3.1冒泡排序
- 2.3.2快速排序
- 2.3.2快速排序的优化
- 2.3.3快速排序
- 2.3.5非递归实现快速排序
- 2.4 归并排序
- 2.4.1递归实现归并排序
- 2.4.2非递归的归并排序
- 3.排序的总结
- 计数排序
1.排序
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
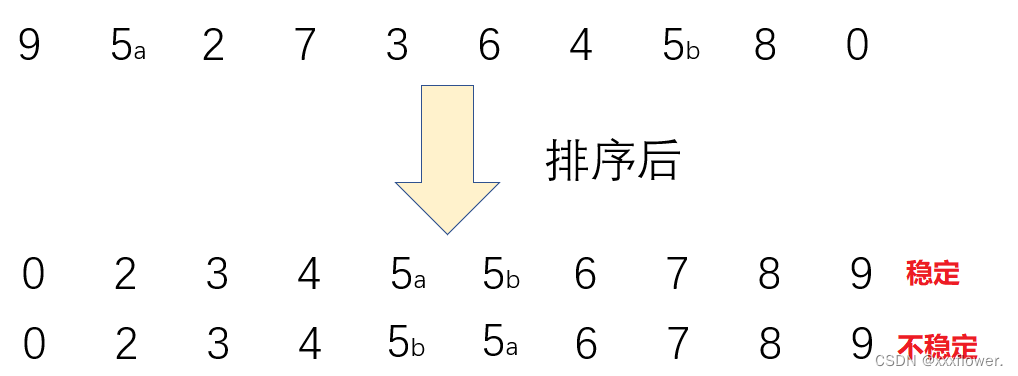
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序的要求不能在内外存之间移动数据的排序。
1.2常见的排序算法
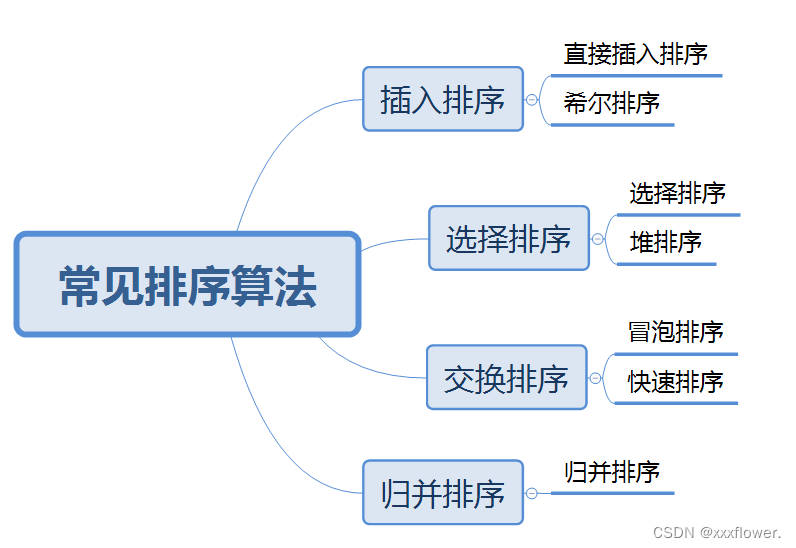
2.常见排序算法
2.1插入排序
插入排序的基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。实际中我们玩扑克牌时,就用了插入排序的思想。
2.1.1直接插入排序
public static void insertSort(int[] array){for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for (;j >= 0;j--) {if(array[j] > tmp){array[j+1] = array[j];}else{break;}}array[j+1] = tmp;}}
我们来分析一下插入排序时间复杂度:
最好情况下:顺序。O(N)
最坏情况下:逆序。O(N^2)
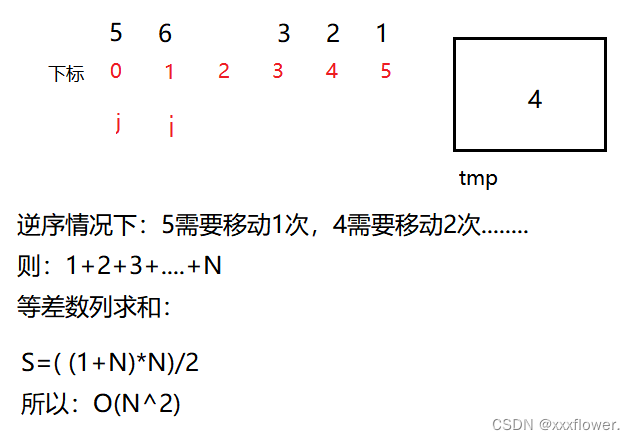
因此我们可以得出一个结论:当数据量不多,且基本上趋于有序的时候,直接插入排序是非常快的。
空间复杂度:O(1)
稳定性:稳定
2.1.2希尔排序(缩小增量排序)
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
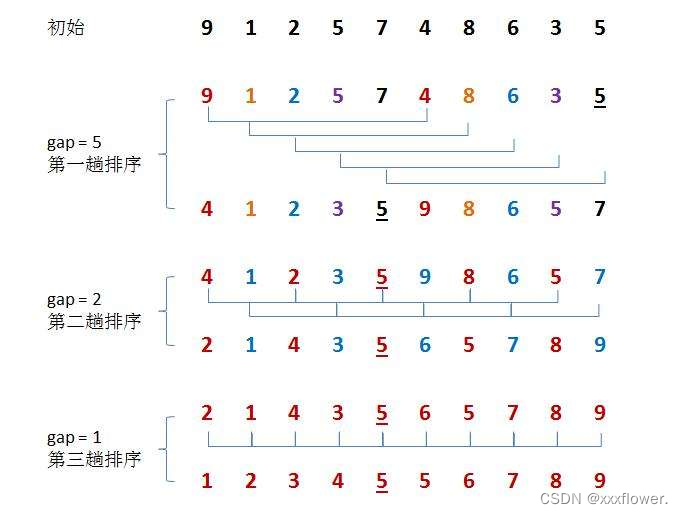
//希尔排序private static void shell(int[] array,int gap){for(int i = gap;i < array.length;i++){int tmp = array[i];int j = i - gap;for(;j >= 0;j -= gap){if(tmp > array[j]){array[j+gap] = array[j];}else{break;}}array[i+gap] = tmp;}}public static void shellSort(int[] array){int gap = array.length;while(gap > 1){gap /= 2;shell(array,gap);}}
希尔排序的时间复杂度是数学上未解决的题,它会随着组别的变化而变化。但是大量的实验的得出局部的结论:O(N^1.3)
稳定性:不稳定。
空间复杂度:O(1)。
希尔排序实际上是对直接插入排序的优化。它使得数字趋于有序化,最后在进行直接插入排序。
2.2选择排序
2.2.1基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
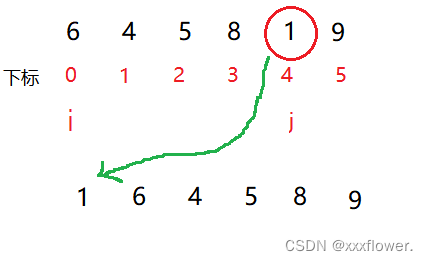
方法一:
//选择排序public static void selectSort(int[] array){for(int i = 0;i < array.length;i++){int minIndex = i;for(int j = i+1;j < array.length;j++){if(array[j] < array[minIndex]) {minIndex = j;}}//处理两个下标一样的情况,比如第一个数就是最大值,后面找不到比它小的值if(i != minIndex){swap(array,minIndex,i);}}}public static void swap(int[] array,int i,int j){int tmp =array[i];array[i] = array[j];array[j] = tmp;}
方法二:
//为了提高效率,可以左右一起找,找最小值放在前面,找最大值放在后面public static void selectSort2(int[] array){int left = 0;int right = array.length -1;while(left < right){int minIndex = left;int maxIndex = right;for(int j = left + 1;j <= right;j++){if(array[j] < array[minIndex]){minIndex = j;}if(array[j] > array[maxIndex]){maxIndex = j;}}//将最小值换到前面swap(array,minIndex,left);//如果max下标正好是Left说明上次已经把最大值从left位置换到了minIndex位置if(maxIndex == left){maxIndex = minIndex;}//吧最大值换到后面。swap(array,maxIndex,right);left++;right--;}}
选择排序的时间复杂度为:O(n^2)
空间复杂度:O(1)
稳定性:不稳定
2.2.3 堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
堆排序将要排序的数组创建成一个大根堆,再将第一个值和最后一个值进行交换,再将二叉树调整成为大根堆,依次循环排序。
//堆排序public static void heapSort(int[] array){creatBigHeap(array);int end = array.length -1;while(end > 0){swap(array,0,end);shiftDown(array,0,end);end--;}}private static void creatBigHeap(int[] array){for(int parent = (array.length - 1-1)/2;parent >= 0;parent--){shiftDown(array,parent,array.length);}}private static void shiftDown(int[] array,int parent,int len){int child = (2* parent) + 1;while(child < len){if(child+1 < len && array[child] < array[child+1]){child++;}if(array[child] > array[parent]){swap(array,child,parent);parent = child;child = 2 * parent +1;}else{break;}}}
堆排序的时间复杂度:O(N*logN)
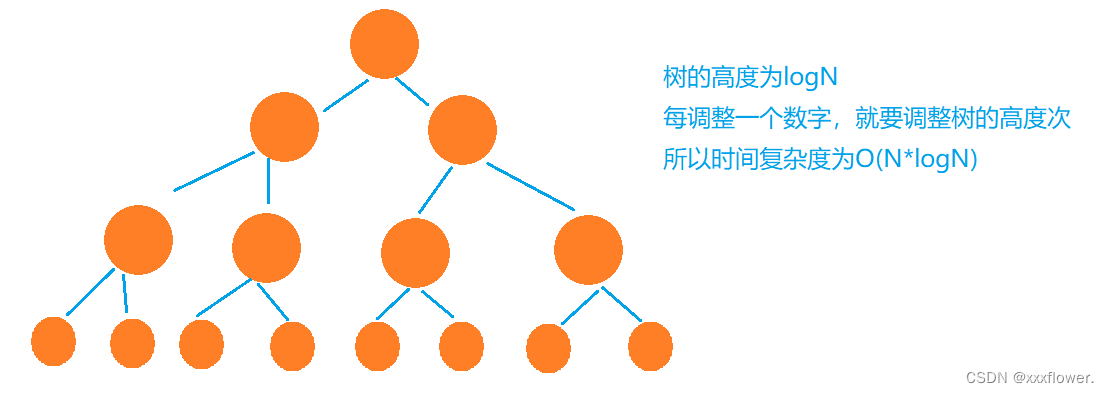
空间复杂度:O(1)
稳定性:不稳定
2.3交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
2.3.1冒泡排序
//冒泡排序public static void bubbleSort(int[] array){for(int i = 0;i < array.length;i++){boolean flg = false;for(int j = 0; j < array.length - 1-i;j++){if(array[j] > array[j+1]){swap(array,j,j+1);flg = true;}}if(flg == false){break;}}}
2.3.2快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
1.Hoare排序
hoare排序是从右边开始找一个比key值小的,从左边找一个比key值大的数,两者进行交换,当left==right时,将此数与key交换。以此来排序。
//快速排序public static int partitionHoare(int[] array,int left,int right){int key = array[left];int i = left;while(left < right){while(left < right && array[right] >= key){right--;}while(left < right && array[left] <= key){left++;}swap(array,left,right);}swap(array,left,i);return left;}
- 挖坑法
挖坑法就是以第一个数字为基准值,从右边找到一个比基准值大的数字放进基准的位置。再从左边找一个比基准值小的数字放进右边的位置
//挖坑法public static int partition2(int[] array,int left,int right){int key = array[left];while(left < right){while(left < right && array[right] >= array[key]){right--;}array[left] = array[right];while(left < right && array[left] <= array[right]){left++;}array[right] = array[left];}array[left] = key;return left;}
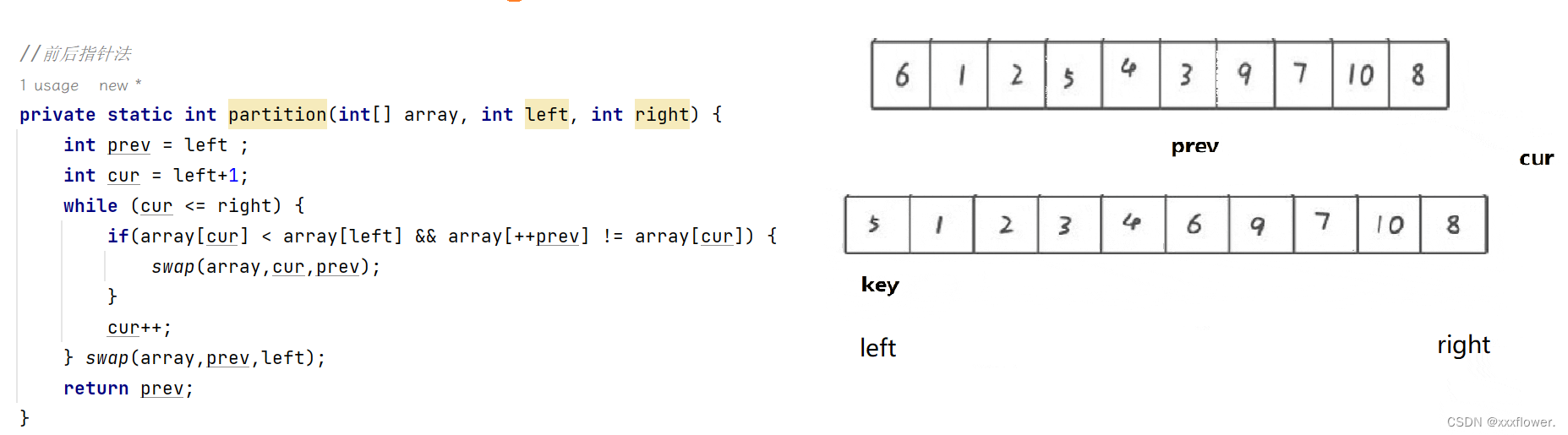
- 前后指针法
//前后指针法private static int partition(int[] array, int left, int right) {int prev = left ;int cur = left+1;while (cur <= right) {if(array[cur] < array[left] && array[++prev] != array[cur]) {swap(array,cur,prev);}cur++;} swap(array,prev,left);return prev;}
2.3.2快速排序的优化
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序
public static void insertSort(int[] array,int left,int right){for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for (;j >= 0;j--) {if(array[j] > tmp){array[j+1] = array[j];}else{break;}}array[j+1] = tmp;}}
public static void quick(int[] array,int start,int end){if(start >= end){return;}if(end - start + 1 <= 15){insertSort(array,start,end);return;}int index = findMidValIndex(array,start,end);swap(array,start,index);int key = partition(array,start,end);quick(array,start,key-1);quick(array,end,key+1);}public static int findMidValIndex(int[] array,int start,int end){int midIndex = (start + end)/2;if(array[start] > array[end]){if(array[midIndex] > array[start]){return start;} else if (array[midIndex] < array[end]) {return end;}else{return midIndex;}}else{if(array[midIndex] < array[start]){return start;} else if (array[midIndex] > array[end]) {return end;}else{return midIndex;}}}
2.3.3快速排序
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
2.3.5非递归实现快速排序

先找基准
判断基准元素左边和右边是否有两个及以上元素?
如果有,则将首位置和p-1位置放入栈中(注意放入顺序)(处理左边),再将p+1位置和end位置放入栈中(处理右边)
当栈不为空的时候弹出两个元素在判断左边和右边的情况。依次循环
//非递归实现快速排序public static void quickSort(int[] array){Stack<Integer> stack = new Stack<>();int start = 0;int end = array.length-1;int pivot = partition(array,start,end);//1.判断左边是否有两个元素if(pivot > start + 1){stack.push(start);stack.push(pivot-1);}//2.判断右边是否有两个元素if(pivot < end-1){stack.push(pivot+1);stack.push(end);}while(!stack.isEmpty()){end = stack.pop();start = stack.pop();pivot = partition(array,start,end);//3.判断左边是否有两个元素if(pivot > start + 1){stack.push(start);stack.push(pivot-1);}//4.判断右边是否有两个元素if(pivot < end-1){stack.push(pivot+1);stack.push(end);}}}
2.4 归并排序
2.4.1递归实现归并排序
归并排序,首先要了解二叉树的基本知识,通过递归将数组分成一个一个的然后在合并。合并的时候可以参考前面写过的例题即两个有序数组合并问题。通过合并可以使数组有序,此时我们建立了新的数组。注意在最后给数组赋值的时候,tmpArr当中的数据是right left之间的有序数据。因此要从右侧开始。
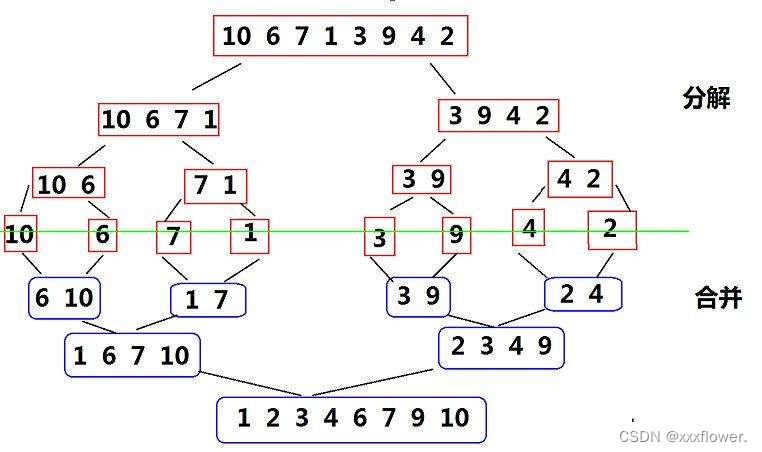
public static void mergeSort1(int[] array){mergeSortChild(array,0,array.length-1);}private static void mergeSortChild(int[] array,int left,int right){if(left == right){return;}//拆分int mid = (left+right)/2;mergeSortChild(array,left,mid);mergeSortChild(array,mid+1,right);//合并merge(array,left,mid,right);}public static void merge(int[] array,int left,int mid,int right){int s1 = left;int e1 = mid;int s2 = mid +1;int e2 = right;int[] tmpArr = new int [right - left +1];int k = 0;while(s1 <= e1 && s2 <= e2){if(array[s1] <= array[s2]){tmpArr[k++] = array[s1++];}else{tmpArr[k++] = array[s2++];}}while(s1 <= e1){tmpArr[k++] = array[s1++];}while(s2 <= e2){tmpArr[k++] = array[s2++];}for(int i = 0;i < k;i++){array[i+left] = tmpArr[i];}}
由归并排序的思想可得,其
空间复杂度为:O(N)
时间复杂度为:O(N*logN)
稳定性:稳定
我们学过的稳定排序为:插入,冒泡,归并
2.4.2非递归的归并排序
非递归实现归并排序时,先将数组分成一个一个的,然后通过调整left,mid right来合并数组。
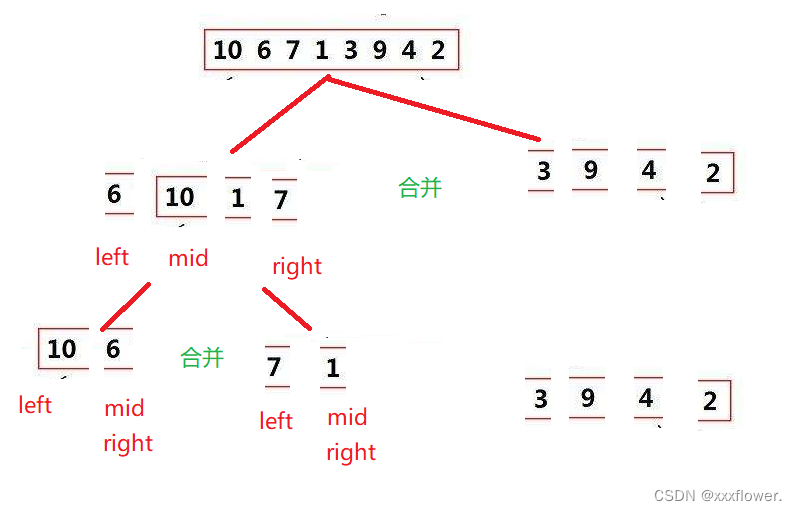
//非递归实现归并排序public static void mergeSort(int[] array){int gap = 1;while(gap < array.length){for(int i = 0;i < array.length;i+=gap){int left = i;int mid = left + gap-1;int right = mid+gap;//需要考虑mid和right越界的问题,i在循环中,所以不用考虑i越界的问题if(mid >= array.length){mid = array.length -1;}if(right >= array.length){right = array.length-1;}merge(array,left,mid,right);}gap = 2*gap;}}
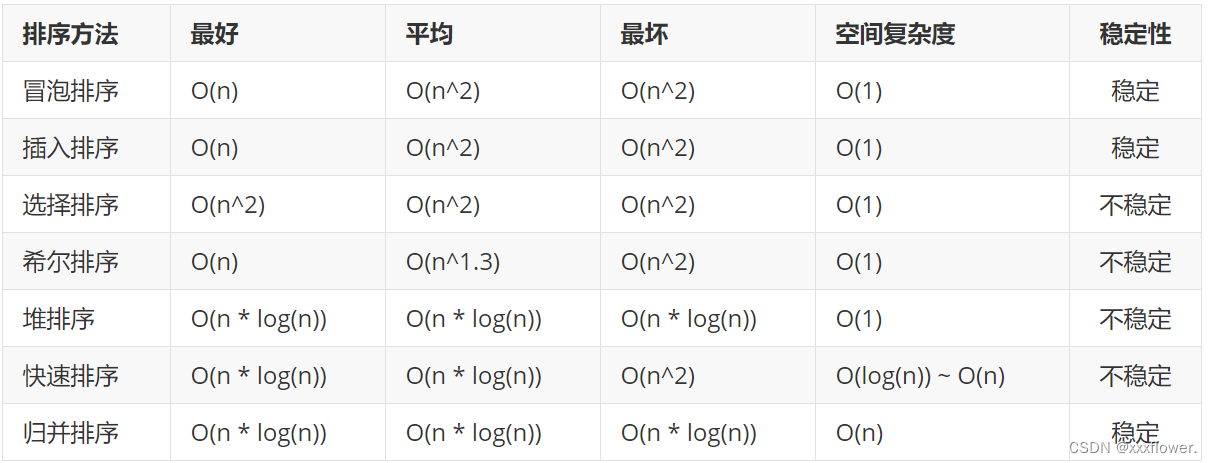
3.排序的总结
计数排序
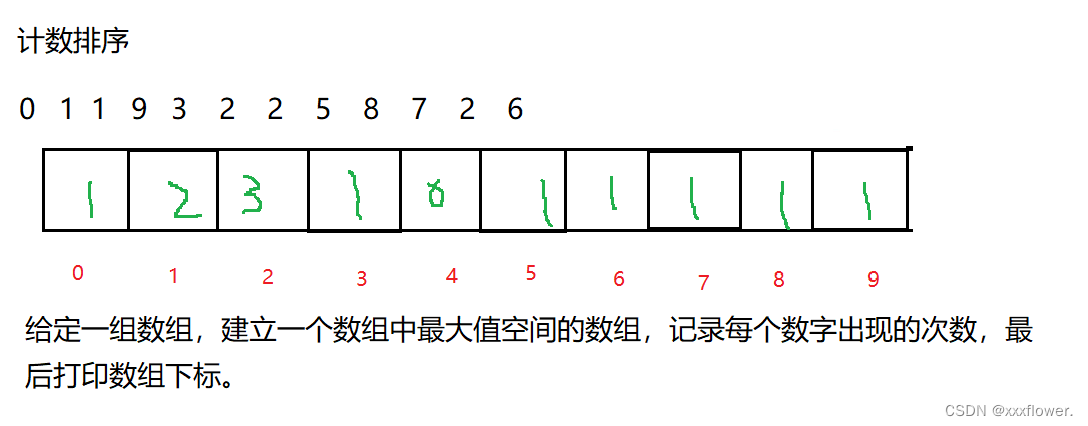
public static void countSort(int[] array) {//1、遍历数组 找到 最小值 和最大值 -》 才能确定 计数数组的大小int maxVal = array[0];int minVal = array[0];//O(n)for (int i = 0; i < array.length; i++) {if(array[i] > maxVal) {maxVal = array[i];}if(array[i] < minVal) {minVal = array[i];}}//2、确定计数数组的长度int len = maxVal - minVal + 1 ;int[] countArr = new int[len];//3. 开始遍历 当前数组 统计每个数字出现的次数 O(n)for (int i = 0; i < array.length; i++) {int val = array[i];countArr[val-minVal] ++;//??????????????}int index = 0;//4. 遍历计数数组,看每个下标的值是几,就打印几个下标的数据就好了 O(范围 + n)//范围遍历一次,位置上所有的数的个数加起来等于nfor (int i = 0; i < countArr.length; i++) {while (countArr[i] > 0) {//不敢打印array[index] = i+minVal;//??????????????index++;countArr[i]--;}}}
相关文章:

【数据结构】排序
作者:✿✿ xxxflower. ✿✿ 博客主页:xxxflower的博客 专栏:【数据结构】篇 语录:⭐每一个不曾起舞的日子,都是对生命的辜负。⭐ 文章目录1.排序1.1排序的概念1.2常见的排序算法2.常见排序算法2.1插入排序2.1.1直接插入…...

过拟合、验证集、交叉验证
过拟合 简单描述:训练集误差小,测试集误差大,模型评估指标的方差(variance)较大; 判断方式: 1、观察 train set 和 test set 的误差随着训练样本数量的变化曲线。 2、通过training accuracy 和…...

原力计划来了【协作共赢 成就未来】
catalogue🌟 写在前面🌟 新星计划持续上新🌟 原力计划方向🌟 原力计划拥抱优质🌟 AIGC🌟 参加新星计划还是原力计划🌟 创作成就未来🌟 写在最后🌟 写在前面 哈喽&#x…...

一文了解Jackson注解@JsonFormat及失效解决
背景 项目中使用WRITE_DATES_AS_TIMESTAMPS: true转换日期格式为时间戳未生效。如下: spring:jackson:time-zone: Asia/Shanghaiserialization:WRITE_DATES_AS_TIMESTAMPS: true尝试是否关于时间的注解是否会生效,使用JsonForma和JsonFiled均失效。 常…...
webpack——使用、分析打包代码
世上本无nodejs js最初是在前端浏览器上运行的语言,js代码一旦脱离了浏览器环境,就无法被运行。直到nodejs的出现,我们在电脑上配置了node环境,就可以让js代码脱离浏览器,在node环境中运行。 浏览器不支持模块化 nodej…...
libvirt零知识学习5 —— libvirt源码编译安装(3)
接前一篇文章libvirt零知识学习4 —— libvirt源码编译安装(2) 在上篇文章及上上篇文章中构建libvirt的时候遇到了一个问题“ERROR: Problem encountered: YAJL 2 is required to build QEMU driver”。上篇文章讲到即使安装了相应的YAJL库仍然不能解决问…...

Nmap 的使用教程
Nmap是一个网络侦测和安全审计工具。它可以用于发现网络上的主机和服务,并提供广泛的信息,其中包括操作系统类型和版本、应用程序和服务的详细信息等。在本文中,我们将介绍如何使用Nmap扫描网络主机,识别开放端口以及进行操作系统…...
async与await异步编程
ECMA2017中新加入了两个关键字async与await 简单来说它们是基于promise之上的的语法糖,可以让异步操作更加地简单明了 首先我们需要用async关键字,将函数标记为异步函数 async function f() {} f()异步函数就是指:返回值为promise对象的函…...
移动应用架构设计:如何转变开发流程
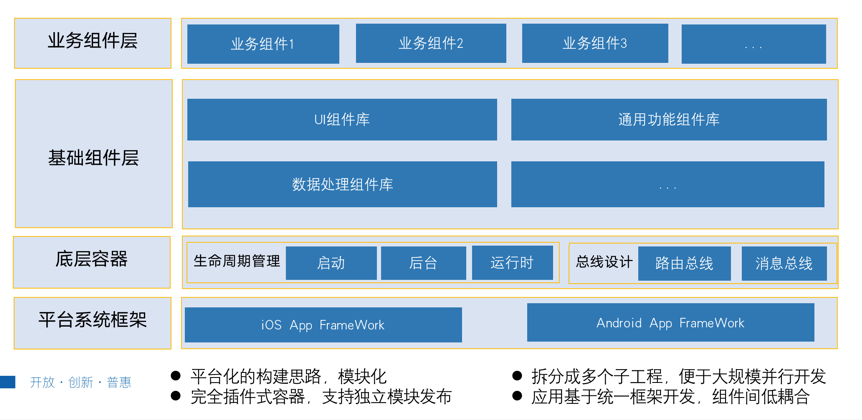
移动应用架构设计:如何转变开发流程 2023 年掌握移动应用程序架构的指南(附案例研究) 如果他们要解决这个问题,开发人员需要了解移动架构设计的最佳实践,使他们能够构建用户喜欢的优化应用程序。其中一些做法包括使用…...

NX二次开发 图层函数总结
简介: NX二次开发 图层相关的总结。 函数: uc5007()uc5008()uc5009()UF_LAYER_ask_category_info()获取图层类别的信息UF_LAYER_ask_category_tag()根据图层分类名称查询其图层分类标识UF_LAYER_ask_status()UF_LAYER_ask_work_layer()UF_LAYER_create…...
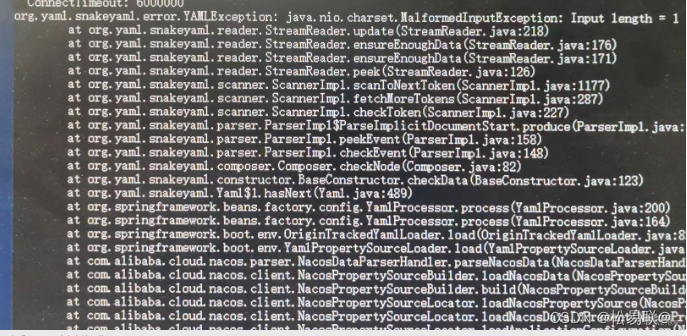
windows微服务部署
windows部署一.nginx部署1.nginx 官网下载2. 配置nginx3.配置nigix 防止nigix刷新404不生效二.配置redis部署成服务1.在系统配置中 配置为系统变量2.打开快捷登录服务管理#3. 开启redis三.windows部署jar包一.nginx部署 1.nginx 官网下载 地址 官网地址 安装 windows版本 可安…...
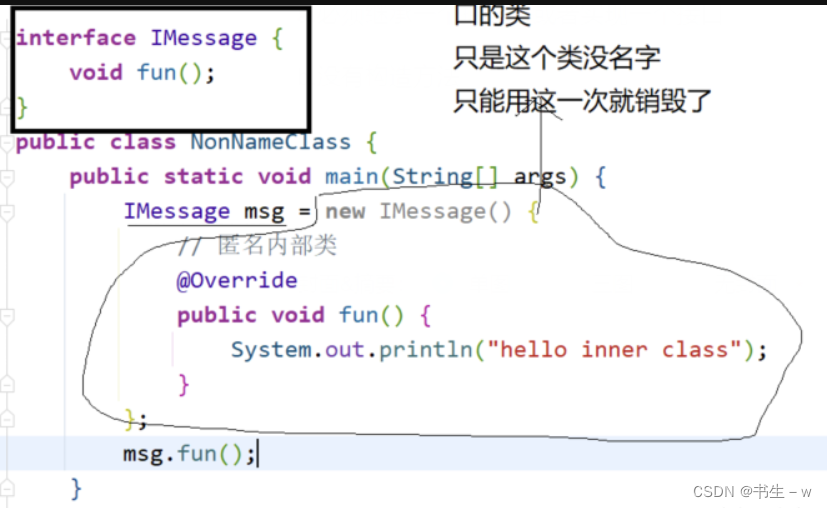
Java四种内部类(看这一篇就够了)
🎉🎉🎉点进来你就是我的人了 博主主页:🙈🙈🙈戳一戳,欢迎大佬指点!人生格言:当你的才华撑不起你的野心的时候,你就应该静下心来学习! 欢迎志同道合的朋友一起加油喔🦾&am…...

蓝桥杯刷题第二十天
第一题:纸张尺寸问题描述在 ISO 国际标准中定义了 A0 纸张的大小为 1189mm 841mm, 将 A0 纸 沿长边对折后为 A1 纸, 大小为 841mm 594mm, 在对折的过程中长度直接取 下整 (实际裁剪时可能有损耗)。将 A1 纸沿长边对折后为 A2 纸, 依此类推。输入纸张的名称, 请输出…...
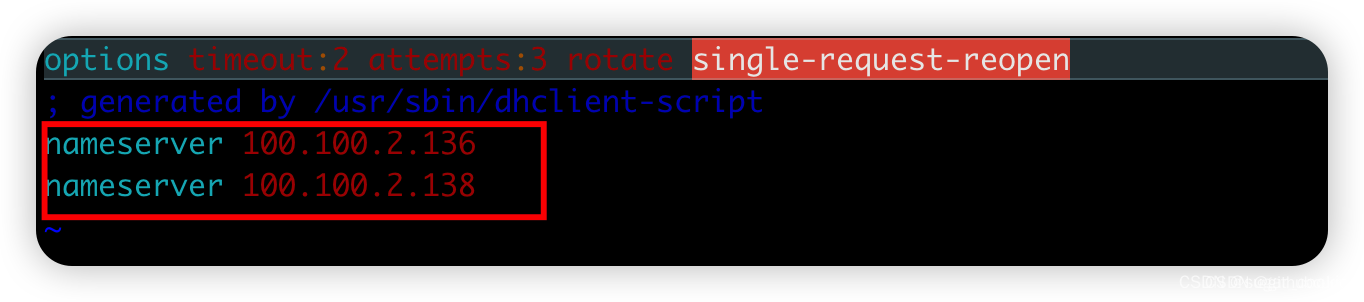
如何通过命令行查看CentOS版本信息和linux系统信息
1.如何查看已安装的CentOS版本信息: 1.cat /proc/version 2.uname -a 3.uname -r 4.cat /etc/centos-release 5.lsb_release -a 6.hostnamectl1. 第一种方式输出的结果是: Linux version 3.10.0-1127.el7.x86_64 (mockbuildkbuilder.bsys.centos.org) …...

oracle查询表空间大小以及每个表所占空间的大小
1、查询数据库中所有的表空间以及表空间所占空间的大小,直接执行语句就可以了: select tablespace_name, sum(bytes)/1024/1024 from dba_data_files group by tablespace_name; 2、查看表空间物理文件的名称及大小 select tablespace_name, file_id, …...
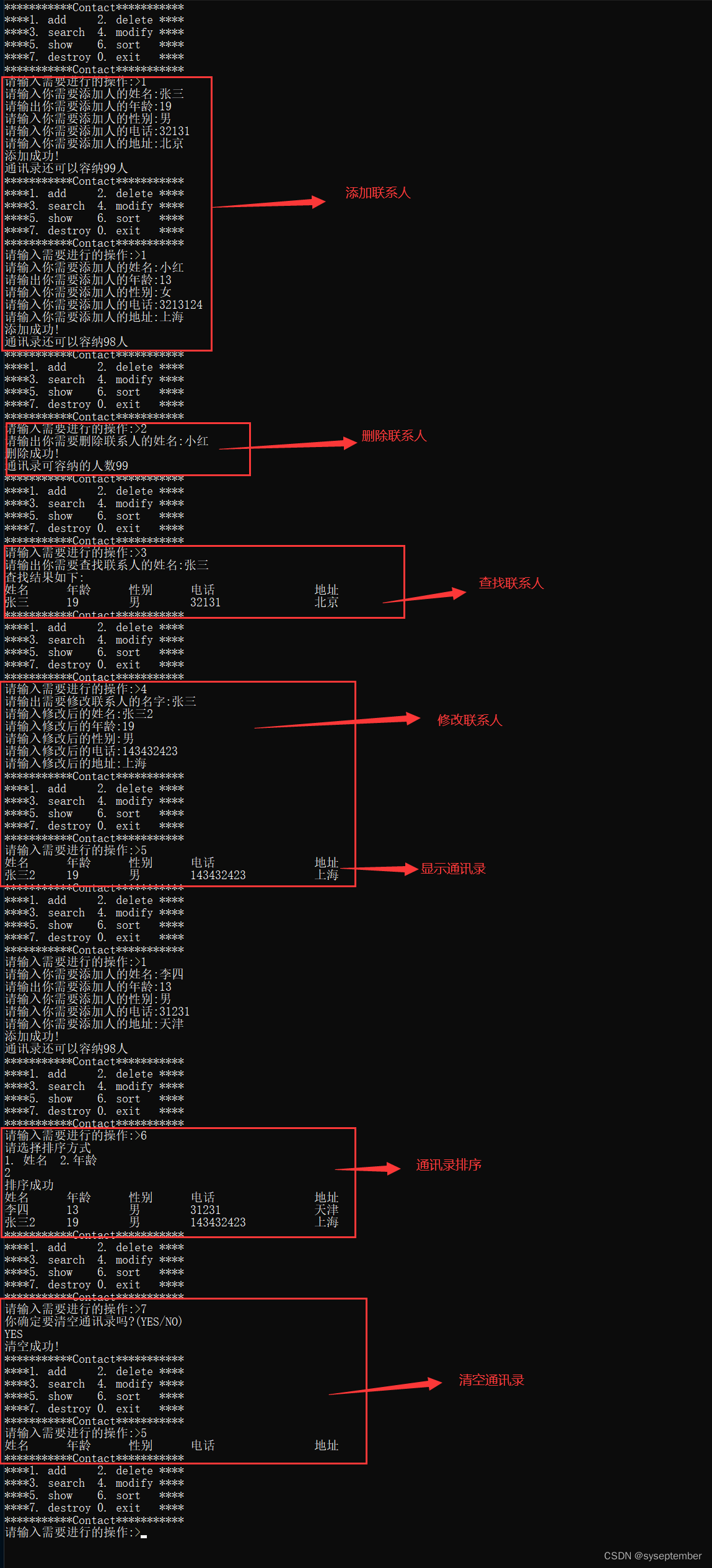
C语言通讯录应用程序:从设计到实现
hello,这期给大家带来C语言实现静态通讯录,主要也是建立起创建大项目的思维,与往期这两篇博客有点类似 C语言实现三子棋 C语言实现扫雷 文章目录🤓通讯录介绍😶🌫️效果演示🤠主题框架头文件测试文件函数…...
银河麒麟v10sp2安装nginx
nginx官网下载:http://nginx.org/download/ 银河麒麟系统请先检查yum源是否配置,若没有配置请参考:https://qdhhkj.blog.csdn.net/article/details/129680789 一、安装 1、yum安装依赖 yum install gcc gcc-c make unzip pcre pcre-devel …...

华为笔试题OD
华为笔试题OD 1题 华为od-2022.11.5-k优雅阈值 题目内容 如果一个数组中出现次数最多的元素出现大于等于 �k 次, 被称为 �−优雅数组k−优雅数组 , �k 也可以被称为优雅阈值。 例如,数组 [1,2,3,1,2,3,…...

Win10+Anconda安装.whl文件到指定环境——以pycocotools为例
Anconda安装.whl文件到指定环境1.Whl文件2.pycocotools安装前言:本篇文章主要记录了两个问题: (1)Win10环境下,利用Anconda安装.whl文件到指定环境的方法; (2)Win10系统安装pycocoto…...

全自动托盘四向穿梭车|拥有输送系统提升机AGV的托盘四向穿梭车立体库的软硬件配置系统
托盘四向穿梭车一般是在两向穿梭车的结构上设计改进而来的,托盘两向穿梭车在取货时可以实现“先进先出”或“先入后出”模式,多用于量大且品种少的行业。但是随着市场的不断迅速发展,各大企业、商家不仅对于小批量、多批次的需求越来越大&…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
