深度学习——神经网络(neural network)详解(二). 带手算步骤,步骤清晰0基础可看
深度学习——神经网络(neural network)详解(二). 手算步骤,步骤清晰0基础可看
前文如下:深度学习——神经网络(neural network)详解(一). 带手算步骤,步骤清晰0基础可看
运用神经网络模型进行房价预测具体手算过程,具体示例
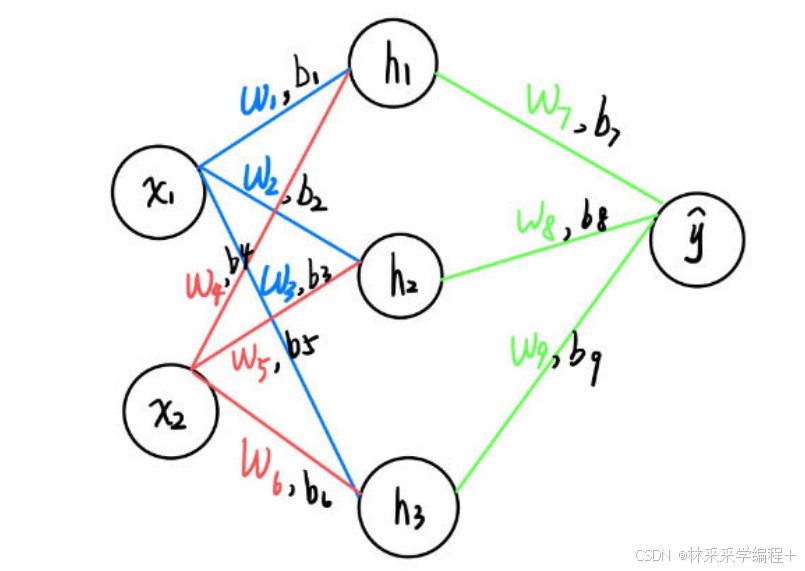
假设我们有一个简单的神经网络,还是之前这个神经网络,输入层2个节点,隐藏层3个节点,输出层1个节点。我们使用以下简化的示例数据:
(一)函数介绍
-
Sigmoid 函数:我们把Sigmoid 函数作为激活函数,用于数组的映射转换,公式为:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1 -
Sigmoid 函数的导数:反向传播中计算梯度所需的导数,公式为:
σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \sigma'(z) = \sigma(z)(1 - \sigma(z)) σ′(z)=σ(z)(1−σ(z)) -
均方误差(MSE)损失函数:衡量预测值与实际值差异的指标,公式为:
L = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 L = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y}_i)^2 L=n1i=1∑n(yi−y^i)2
在单样本情况下简化为:
L = ( y − y ^ ) 2 L = (y - \hat{y})^2 L=(y−y^)2 -
均方误差(MSE)损失函数的导数:
在单样本情况下简化为:
∂ L ∂ y ^ = − 2 ( y − y ^ ) \frac{\partial L}{\partial \hat{y}} = -2(y-\hat{y}) ∂y^∂L=−2(y−y^)
4.权重的梯度
涉及到 w 1 w_{1} w1的公式如下:
L = ( y − y ^ ) 2 L = (y - \hat{y})^2 L=(y−y^)2
y ^ = σ ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) \hat{y} = \sigma(w_7 h_1 + w_8 h_2 + w_9 h_3) y^=σ(w7h1+w8h2+w9h3)
h 1 = σ ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) h_1 = \sigma(w_{1}x_1 + b_1+ w_{4}x_2 + b_4) h1=σ(w1x1+b1+w4x2+b4)
比如对于 w 1 w_{1} w1,其求梯度公式为:
d L d w 1 = d L d y ^ ⋅ d y ^ d h 1 ⋅ d h 1 d w 1 \frac{dL}{dw_{1}} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh_{1}} \cdot \frac{dh_{1}}{dw_{1}} dw1dL=dy^dL⋅dh1dy^⋅dw1dh1
(1) d L d y ^ = − 2 ( y − y ^ ) \frac{dL}{d\hat{y}}=-2(y-\hat{y}) dy^dL=−2(y−y^)
(2)计算 d y ^ d h 1 \frac{d\hat{y}}{dh_{1}} dh1dy^
令 z = w 7 h 1 + w 8 h 2 + w 9 h 3 z=w_7 h_1 + w_8 h_2 + w_9 h_3 z=w7h1+w8h2+w9h3,
则 y ^ = σ ( z ) = σ ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) \hat{y}=\sigma(z)=\sigma(w_7 h_1 + w_8 h_2 + w_9 h_3) y^=σ(z)=σ(w7h1+w8h2+w9h3),
而 σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \sigma'(z) = \sigma(z)(1 - \sigma(z)) σ′(z)=σ(z)(1−σ(z))
所以
d y ^ d h 1 = σ ( z ) ⋅ ( 1 − σ ( z ) ) ⋅ d z d h 1 \frac{d\hat{y}}{dh_{1}}=\sigma(z)\cdot(1 - \sigma(z))\cdot\frac{dz}{dh_{1}} dh1dy^=σ(z)⋅(1−σ(z))⋅dh1dz
d y ^ d h 1 = ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ⋅ ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) ⋅ w 7 \frac{d\hat{y}}{dh_{1}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_7 dh1dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w7
(3)同理计算 d h 1 d w 1 \frac{dh_{1}}{dw_{1}} dw1dh1
h 1 = σ ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) h_1 = \sigma(w_{1}x_1 + b_1+ w_{4}x_2 + b_4) h1=σ(w1x1+b1+w4x2+b4)
d h 1 d w 1 = ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) ⋅ ( 1 − ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) ) ⋅ x 1 \frac{dh_{1}}{dw_{1}}=(w_{1}x_1 + b_1+ w_{4}x_2 + b_4)\cdot(1 - (w_{1}x_1 + b_1+ w_{4}x_2 + b_4))\cdot x_1 dw1dh1=(w1x1+b1+w4x2+b4)⋅(1−(w1x1+b1+w4x2+b4))⋅x1
所以
d L d w 1 = d L d y ^ ⋅ d y ^ d h 1 ⋅ d h 1 d w 1 = − 2 ( y − y ^ ) ⋅ ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) w 7 ⋅ ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) ( 1 − ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) ) x 1 \frac{dL}{dw_{1}} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh_{1}} \cdot \frac{dh_{1}}{dw_{1}}=-2(y-\hat{y}) \cdot (w_7 h_1 + w_8 h_2 + w_9 h_3) (1 - (w_7 h_1 + w_8 h_2 + w_9 h_3)) w_7 \cdot (w_{1}x_1 + b_1+ w_{4}x_2 + b_4) (1 - (w_{1}x_1 + b_1+ w_{4}x_2 + b_4)) x_1 dw1dL=dy^dL⋅dh1dy^⋅dw1dh1=−2(y−y^)⋅(w7h1+w8h2+w9h3)(1−(w7h1+w8h2+w9h3))w7⋅(w1x1+b1+w4x2+b4)(1−(w1x1+b1+w4x2+b4))x1
(二)参数更新过程
1.输入数据(样本)
- 输入特征: X = [ 120 , 1 ] X = [120, 1] X=[120,1](面积120平方米,市中心位置)
- 目标值: y = 300 , 000 y = 300,000 y=300,000(房价300,000元)
2.输入到隐藏层的权重和偏置随机初始化
- 权重 W h = [ w 1 , w 2 , w 3 , w 4 , w 5 , w 6 ] = [ 0.2 , 0.3 , 0.4 , 0.5 , 0.6 , 0.7 ] W_h = [w_1, w_2, w_3, w_4, w_5, w_6] = [0.2, 0.3, 0.4, 0.5, 0.6, 0.7] Wh=[w1,w2,w3,w4,w5,w6]=[0.2,0.3,0.4,0.5,0.6,0.7]
- 偏置 b h = [ b 1 , b 2 , b 3 , b 4 , b 5 , b 6 , b 7 , b 8 , b 9 ] = [ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ] b_h = [b_1, b_2, b_3,b_4, b_5, b_6,b_7, b_8, b_9] = [0, 0, 0,0, 0, 0,0, 0, 0] bh=[b1,b2,b3,b4,b5,b6,b7,b8,b9]=[0,0,0,0,0,0,0,0,0](假设偏置为0)
3.激活函数输出
h 1 = σ ( w 1 ⋅ x 1 + w 4 ⋅ x 2 ) h_1 = \sigma(w_1 \cdot x_1 + w_4 \cdot x_2) h1=σ(w1⋅x1+w4⋅x2)
h 2 = σ ( w 2 ⋅ x 1 + w 5 ⋅ x 2 ) h_2 = \sigma(w_2 \cdot x_1 + w_5 \cdot x_2) h2=σ(w2⋅x1+w5⋅x2)
h 3 = σ ( w 3 ⋅ x 1 + w 6 ⋅ x 2 ) h_3 = \sigma(w_3 \cdot x_1 + w_6 \cdot x_2) h3=σ(w3⋅x1+w6⋅x2)
4.具体计算
h 1 = σ ( 0.2 × 120 + 0.5 × 1 ) = σ ( 24.2 ) h_1 = \sigma(0.2 \times 120 + 0.5 \times 1)=\sigma(24.2) h1=σ(0.2×120+0.5×1)=σ(24.2)
h 2 = σ ( 0.3 × 120 + 0.6 × 1 ) = σ ( 37.8 ) h_2 = \sigma(0.3 \times 120 + 0.6 \times 1)=\sigma(37.8) h2=σ(0.3×120+0.6×1)=σ(37.8)
h 3 = σ ( 0.4 × 120 − 0.7 × 1 ) = σ ( 46.3 ) h_3 = \sigma(0.4 \times 120 - 0.7 \times 1)=\sigma(46.3) h3=σ(0.4×120−0.7×1)=σ(46.3)
假设 σ ( 24.2 ) ≈ 0.99 \sigma(24.2) \approx 0.99 σ(24.2)≈0.99, σ ( 37.8 ) ≈ 0.998 \sigma(37.8) \approx 0.998 σ(37.8)≈0.998, σ ( 46.3 ) ≈ 0.999 \sigma(46.3) \approx 0.999 σ(46.3)≈0.999(这里取Sigmoid函数的近似值)
5.隐藏到输出层的权重
- 权重 W o = [ w 7 , w 8 , w 9 ] = [ 0.1 , 0.2 , 0.3 ] W_o = [w_7, w_8, w_9] = [0.1, 0.2, 0.3] Wo=[w7,w8,w9]=[0.1,0.2,0.3]
6.输出层预测值
y ^ = σ ( w 7 ⋅ h 1 + w 8 ⋅ h 2 + w 9 ⋅ h 3 ) ≈ 0.6452 \hat{y} = \sigma(w_7 \cdot h_1 + w_8 \cdot h_2 + w_9 \cdot h_3)\approx 0.6452 y^=σ(w7⋅h1+w8⋅h2+w9⋅h3)≈0.6452
7.损失计算
L = ( 300 , 000 − y ^ ) 2 ≈ ( 300 , 000 − 0.6452 ) 2 ≈ 89 , 999 , 810 , 000 L = (300,000 - \hat{y})^2 \approx (300,000 - 0.6452 )^2 \approx 89,999,810,000 L=(300,000−y^)2≈(300,000−0.6452)2≈89,999,810,000(这里取 y ^ \hat{y} y^ 的近似值进行计算,这个损失也太大了)
8.梯度计算
(1) d L d y ^ = − 2 ( y − y ^ ) = − 2 ( 300 , 000 − 0.6452 ) ≈ − 599 , 998.7096 \frac{dL}{d\hat{y}}=-2(y-\hat{y})=−2(300,000−0.6452)\approx −599,998.7096 dy^dL=−2(y−y^)=−2(300,000−0.6452)≈−599,998.7096
(2) d y ^ d h 1 / d h 2 / d h 3 \frac{d\hat{y}}{dh_{1}/dh_{2}/dh_{3}} dh1/dh2/dh3dy^
d y ^ d h 1 = ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ⋅ ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) ⋅ w 7 ) ≈ 0.024 \frac{d\hat{y}}{dh_{1}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_7)\approx0.024 dh1dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w7)≈0.024
d y ^ d h 2 = ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ⋅ ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) ⋅ w 8 ) ≈ 0.048 \frac{d\hat{y}}{dh_{2}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_8)\approx0.048 dh2dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w8)≈0.048
d y ^ d h 3 = ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ⋅ ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) ⋅ w 9 ) ≈ 0.07 \frac{d\hat{y}}{dh_{3}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_9)\approx0.07 dh3dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w9)≈0.07
(3) d h 1 d w 1 \frac{dh_{1}}{dw_{1}} dw1dh1
d h 1 d w 1 = ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) ⋅ ( 1 − ( w 1 x 1 + b 1 + w 4 x 2 + b 4 ) ) ⋅ x 1 = − 69090 \frac{dh_{1}}{dw_{1}}=(w_{1}x_1 + b_1+ w_{4}x_2 + b_4)\cdot(1 - (w_{1}x_1 + b_1+ w_{4}x_2 + b_4))\cdot x_1=−69090 dw1dh1=(w1x1+b1+w4x2+b4)⋅(1−(w1x1+b1+w4x2+b4))⋅x1=−69090
d L d w 1 = d L d y ^ ⋅ d y ^ d h 1 ⋅ d h 1 d w 1 = − 599 , 998.7096 × 0.024 × ( − 69090 ) = 994893860 \frac{dL}{dw_{1}} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh_{1}} \cdot \frac{dh_{1}}{dw_{1}}=−599,998.7096\times 0.024\times(−69090)=994893860 dw1dL=dy^dL⋅dh1dy^⋅dw1dh1=−599,998.7096×0.024×(−69090)=994893860
8.梯度更新
这里我们将学习率 α \alpha α设置为0.001。
w 1 n e w = α ⋅ ∂ L ∂ w 1 o l d = 0.001 × 994893860 = 94893.86 w_{1} ^{new}= \alpha \cdot \frac{\partial L}{\partial w_{1}^{old}} =0.001\times994893860 =94893.86 w1new=α⋅∂w1old∂L=0.001×994893860=94893.86
到此为止,我们利用一个样本 [ x 1 , x 2 ] = [ 120 , 1 ] [{x_{1},x_{2}}]=[{120,1}] [x1,x2]=[120,1]和这个简单的神经网络对参数 w 1 w_{1} w1的更新已经完成。
后续步骤就是按照更新 w 1 w_{1} w1的方法对其他参数进行更新,当所有参数都更新完一次后,被称作一次迭代(iteration)。当你拥有的数据集中的所有数据都输入模型被训练一次,被称作一轮(epoch)。我们的模型训练好需要多个轮次,几百轮或者上千轮。
一个简单的神经网络的迭代过程演示到这里就结束了。
相关文章:

深度学习——神经网络(neural network)详解(二). 带手算步骤,步骤清晰0基础可看
深度学习——神经网络(neural network)详解(二). 手算步骤,步骤清晰0基础可看 前文如下:深度学习——神经网络(neural network)详解(一). 带手算步骤&#x…...

【扒网络架构】backbone、ccff
backbone CCFF 还不知道网络连接方式,只是知道了每一层 backbone backbone.backbone.conv1.weight torch.Size([64, 3, 7, 7])backbone.backbone.layer1.0.conv1.weight torch.Size([64, 64, 1, 1])backbone.backbone.layer1.0.conv2.weight torch.Size([64, 64,…...

linux进程
exit()函数正常结束进程 man ps aux 是在使用 ps 命令时常用的一个选项组合,用于显示系统中所有进程的详细信息。aux 不是 ps 命令的一个正式选项,而是三个选项的组合:a, u, 和 x。这三个选项分别代表不同的含义&#…...
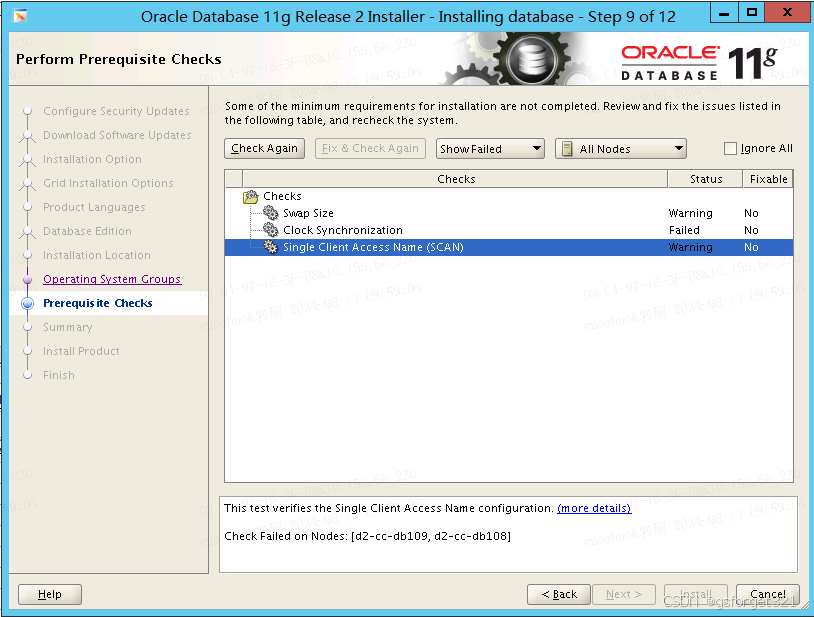
PRVF-4037 : CRS is not installed on any of the nodes
描述:公司要求替换centos,重新安装ORACLE LINUX RAC的数据库做备库,到时候切换成主库,安装Linux7GRID 19C 11G Oracle,顺利安装grid 19c,安装11G数据库软件的时候检测报如题错误:**PRVF-4037 …...

整理 酷炫 Flutter 开源UI框架 FAB
flutter_villains 灵活且易于使用的页面转换。 项目地址:https://github.com/Norbert515/flutter_villains 项目Demo:https://download.csdn.net/download/qq_36040764/89631324...

Unity 编写自己的aar库,接收Android广播(broadcastReceiver)并传递到Unity
编写本文是因为找了很多文章,都比较片段,不容易理解,对于Android新手来说理解起来不友好。我这里写了一个针对比较小白的文章,希望有所帮助。 Android端 首先还是先来写Android端,我们新建一个Android空项目…...

Mysql cast函数、cast用法、字符串转数字、字符串转日期、数据类型转换
文章目录 一、语法二、示例2.1、复杂示例 三、cast与convert的区别 CAST 函数是 SQL 中的一种类型转换函数,它用于将一个数据类型转换为另一个数据类型,这篇文章主要介绍了Mysql中Cast()函数的用法,需要的朋友可以参考下。 Mysql提供了两种将值转换成指…...

微信小程序开发之组件复用机制
新建复用文件,另外需要注册 behavior 例如: 在behavior.js文件中写入方法,并向外暴露出去 写法一: module.exportsBehavior({data: {num: 1},lifetimes: {created() {console.log(1);}} })写法二: const behavior …...

数据结构--线性表
数据结构分类 集合 线性结构(一对一) 树形结构(一对多) 图结构(多对多) 数据结构三要素 1、逻辑结构 2、数据的运算 3、存储结构(物理结构) 线性表分类 1、顺序表 2、链表 3、栈 4、队列 5、串 线性表--顺序表 顺序表的特点 顺序表的删除和插入…...

深入探针:PHP与DTrace的动态追踪艺术
标题:深入探针:PHP与DTrace的动态追踪艺术 在高性能的PHP应用开发中,深入理解代码的执行流程和性能瓶颈是至关重要的。DTrace,作为一种强大的动态追踪工具,为开发者提供了对PHP脚本运行时行为的深入洞察。本文将详细介…...

黑龙江日报报道第5届中国计算机应用技术大赛,赛氪提供赛事支持
2024年7月17日,黑龙江日报、极光新闻对在哈尔滨市举办的第5届中国计算机应用技术大赛全国总决赛进行了深入报道。此次大赛由中国计算机学会主办,中国计算机学会计算机应用专业委员会与赛氪网共同承办,吸引了来自全国各地的顶尖技术团队和选手…...

【计算机网络】LVS四层负载均衡器
https://mobian.blog.csdn.net/article/details/141093263 https://blog.csdn.net/weixin_42175752/article/details/139966198 《高并发的哲学原理》 (基本来自本书) 《亿级流量系统架构设计与实战》 LVS 章文嵩博士创造 LVS(IPVS) 章⽂嵩发…...
)
Java 守护线程练习 (2024.8.12)
DaemonExercise package DaemonExercise20240812;public class DaemonExercise {public static void main(String[] args) {// 守护线程// 当普通线程执行完毕之后,守护线程没有继续执行的必要,所以说会逐步关闭(并非瞬间关闭)//…...

C#小桌面程序调试出错,如何解决??
🏆本文收录于《CSDN问答解惑-专业版》专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收…...

Seatunnel Mysql数据同步到Mysql
环境 mysql-connector-java-8.0.28.jar、connector-cdc-mysql 配置 env {# You can set SeaTunnel environment configuration hereexecution.parallelism 2job.mode "STREAMING"# 10秒检查一次,可以适当加大这个值checkpoint.interval 10000#execu…...

Java Web —— 第五天(请求响应1)
postman Postman是一款功能强大的网页调试与发送网页HTTP请求的Chrome插件 作用:常用于进行接口测试 简单参数 原始方式 在原始的web程序中,获取请求参数,需要通过HttpServletRequest 对象手动获 http://localhost:8080/simpleParam?nameTom&a…...
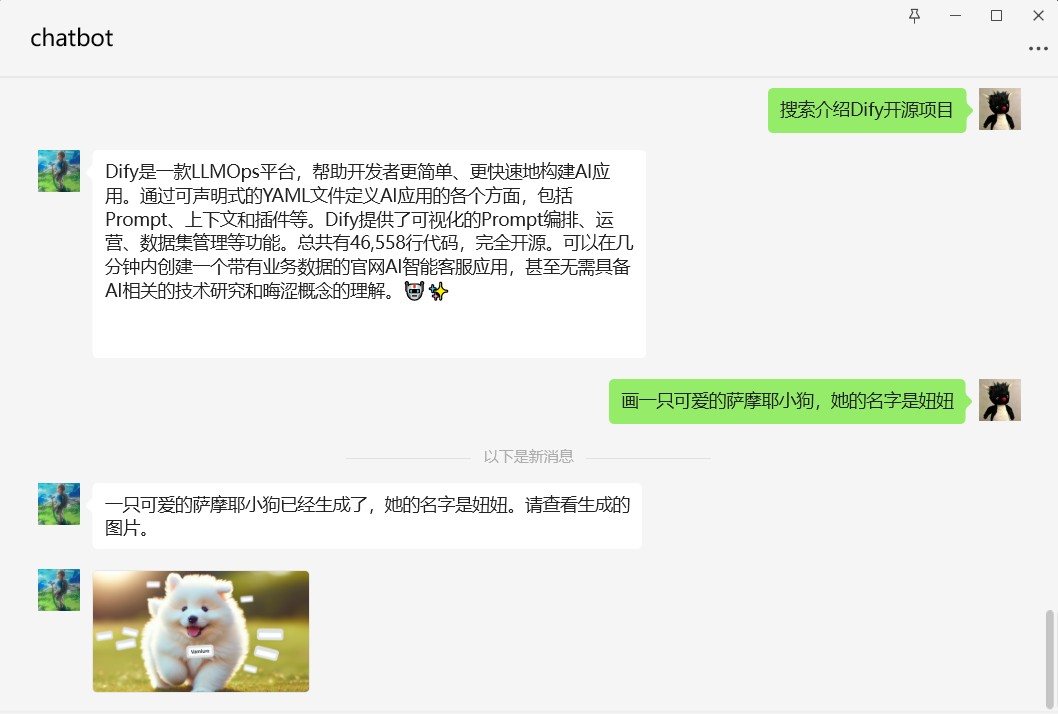
【LLMOps】手摸手教你把 Dify 接入微信生态
作者:韩方圆 "Dify on WeChat"开源项目作者 概述 微信作为最热门即时通信软件,拥有巨大的流量。 微信友好的聊天窗口是天然的AI应用LUI(Language User Interface)/CUI(Conversation User Interface)。 微信不仅有个人微信,同时提供…...
Ftrans文件摆渡方案:重塑文件传输与管控的科技先锋
一、哪些行业会用到文件摆渡相关方案 文件摆渡相关的产品和方案通常用于需要在不同的网络、安全域、网段之间传输数据的场景,主要是一些有核心数据需要保护的行业,做了网络隔离和划分。以下是一些应用比较普遍的行业: 金融行业:…...

LaTeX中的除号表示方法详解
/除号 LaTeX中的除号表示方法详解1. 使用斜杠 / 表示除号优点缺点 2. 使用 \frac{} 表示分数形式的除法优点缺点 3. 使用 \div 表示标准除号优点缺点 4. 使用 \over 表示分数形式的除法优点缺点 5. 使用 \dfrac{} 和 \tfrac{} 表示大型和小型分数优点缺点 总结 LaTeX中的除号表…...

DID、DID文档、VC、VP分别是什么 有什么关系
DID(去中心化身份) 定义:DID 是一种去中心化的唯一标识符,用于表示个体、组织或设备的身份。DID 不依赖于中央管理机构,而是由去中心化网络(如区块链)生成和管理。 用途:DID 允许用…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
