P5821 【LK R-03】密码串匹配
[题目通道](【L&K R-03】密码串匹配 - 洛谷)
一道神题。
如果没有修改操作,翻转A数组或B数组后就是裸的FFT了
-
如果每次操作都暴力修改+FFT时间复杂度显然爆炸
-
如果每次操作都不修改,记下修改序列,询问时加上修改序列的贡献,复杂度仍然爆炸
于是考虑把两种方法结合起来,对操作序列分块
#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#define M 1000005
#define mod 998244353
#define g 3
using namespace std;
int n,ll,m,len=1,L,power3[M],power_inv3[M],rev[M],H,cnt;
int X[M],Y[M],E[M];
long long A[M],B[M],C[M],tmp_A[M],tmp_B[M],len_inv,sum;
long long add(long long u,long long v){return (u+=v)>=mod?u-mod:u;}
long long inv(long long x){return x==1?1:(mod-mod/x)*inv(mod%x)%mod;}
long long power(long long x,long long y){long long ans=1,now=x;for (register long long i=y;i;i>>=1,now=now*now%mod)if (i&1) ans=ans*now%mod;return ans;
}
char get_char(){//快读(字母)char c=getchar();while (c<'a'||c>'z') c=getchar();return c-'a';
}
int read(){//快读(整数)char c=getchar();int ans=0;while (c<'0'||c>'9') c=getchar();while (c>='0'&&c<='9') ans=ans*10+c-'0',c=getchar();return ans;
}
void Write(long long x){//快速输出if (x<10) putchar(x^48);else Write(x/10),putchar((x%10)^48);return;
}
void NTT(long long *A,int flag){//NTT板子for (register int i=0;i<len;i++)if (i<rev[i]) swap(A[i],A[rev[i]]);for (register int l=1;l<len;l<<=1){long long T=(flag==1?power3[l]:power_inv3[l]);for (register int i=0;i<len;i+=(l<<1)){long long t=1;for (register int j=0;j<l;j++,t=t*T%mod){long long u=A[i+j],v=A[i+j+l]*t%mod;A[i+j]=add(u,v),A[i+j+l]=add(u,mod-v);}}}return;
}
void mul(){//多项式乘法for (register int i=0;i<len;i++) tmp_B[i]=B[i];NTT(tmp_B,1);for (register int i=0;i<len;i++) C[i]=tmp_A[i]*tmp_B[i]%mod;NTT(C,-1);for (register int i=0;i<len;i++) C[i]=C[i]*len_inv%mod;return;
}
long long query(int x){//处理询问操作long long now=C[x+ll-1];x+=ll-1;for (register int i=1;i<=X[0];i++) now+=Y[i]*A[x-X[i]];//暴力加上修改块内修改操作贡献return sum+E[x]-(x>=ll?E[x-ll]:0)-now*2;
}
int main(){n=read(),ll=read(),m=read();H=(int)(pow(n*log2(n),0.5))*3;while (len<=n+ll) len<<=1,++L;for (register int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<L-1);for (register int i=0;i<n;i++) tmp_A[i]=A[i]=get_char(),E[i]=E[i-1]+A[i]*A[i];for (register int i=0;i<ll;i++) B[i]=get_char(),sum+=B[i]*B[i];for (register int i=0,j=ll-1;i<j;i++,j--) swap(B[i],B[j]);for (register int l=1;l<len;l<<=1) power3[l]=power(g,(mod-1)/(l<<1)),power_inv3[l]=power(inv(g),(mod-1)/(l<<1));len_inv=inv(len);NTT(tmp_A,1);mul();//对密码串T只需要做一次FFTfor (register int i=1,opt;i<=m;i++){opt=read();if (opt==1) Write(query(read()-1)),putchar('\n');else {X[++X[0]]=ll-read(),Y[++Y[0]]=get_char();sum-=B[X[X[0]]]*B[X[X[0]]];int tmp=B[X[X[0]]];B[X[X[0]]]=Y[Y[0]],Y[Y[0]]-=tmp;sum+=B[X[X[0]]]*B[X[X[0]]];}if (X[0]==H) mul(),X[0]=Y[0]=0;//块的末尾暴力做NTT}return 0;
}相关文章:

P5821 【LK R-03】密码串匹配
[题目通道](【L&K R-03】密码串匹配 - 洛谷) 一道神题。 如果没有修改操作,翻转A数组或B数组后就是裸的FFT了 如果每次操作都暴力修改FFT时间复杂度显然爆炸 如果每次操作都不修改,记下修改序列,询问时加上修改序列的贡献,…...

httpx,一个网络请求的 Python 新宠儿
大家好!我是爱摸鱼的小鸿,关注我,收看每期的编程干货。 一个简单的库,也许能够开启我们的智慧之门, 一个普通的方法,也许能在危急时刻挽救我们于水深火热, 一个新颖的思维方式,也许能…...

计算机网络408考研 2014
1 计算机网络408考研2014年真题解析_哔哩哔哩_bilibili 1 111 1 11 1...

JavaScript 资源大全中文版
目录 JavaScript资源大全中文版 包管理器加载器组件管理器打包工具测试框架QA工具MVC 框架和库基于 Node 的 CMS 框架模板引擎文章和帖子数据可视化 时间轴电子表格 编辑器文档工具 文件函数式编程响应式编程数据结构日期字符串数字存储颜色国际化和本地化控制流路由安全性日志…...

如何获取能直接在浏览器打开的播放地址?
背景:需要在浏览器上直接打开设备的画面,但又不想二次开发 本文介绍一种极简的取流方式,不需要掌握前端开发知识,按照本文档拼接就能得到设备的播放地址 一、准备工作 1.将设备接入到萤石账号下。萤石设备接入指南:h…...

如何用 LangChain 实现一个Zero Shot智能决策器(附源码)
写在前面 最近一直在研究Agent和Tool的使用,今天给大家带来一篇何枝大佬(知乎何枝)的文章《如何用LangChain实现一个Zero Shot智能决策器》,并附上源码。 知乎:https://zhuanlan.zhihu.com/p/627333499LangChain是当…...

读完这本书,我终于搞懂了Transformer、BERT和GPT!【附PDF】
前言 《Transformer、BERT和GPT: 包括ChatGPT和提示工程》 是一本深入浅出地介绍自然语言处理领域前沿技术的专著,全书一共379页PDF,是截止到目前比较系统介绍NLP和GPT融合领域的书籍。 全书共十章,内容丰富,结构清晰,…...
)
仿RabbitMq简易消息队列基础篇(Muduo库的使用)
TOC Muduo库简介 Muduo由陈硕⼤佬开发,是⼀个基于⾮阻塞IO和事件驱动的C⾼并发TCP⽹络编程库。他是一款基于主从Reactor模型的网络库,其使用的线程模型是one loop per thread, 所谓 one loop per thread 指的是: 一个线程只能有一个事件循…...

.net SqlSugarHelper
NuGet安装: SqlSugarCore using SqlSugar; using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;namespace Namespace {public class SqlSugarHelper{public string _connectionString Custom…...

“AI能不能代替某某职业”,到底谁在破防?
前几天,公司在午间分享时谈到一个有趣的辩题:“AI能不能代替产品经理”,不仅双方辩手打了个你来我往,就连下面的吃瓜群众也进入红温状态。 “AI能不能代替xx”已经成为一个普遍的话题,在某乎上随手一刷就是不同的职业…...
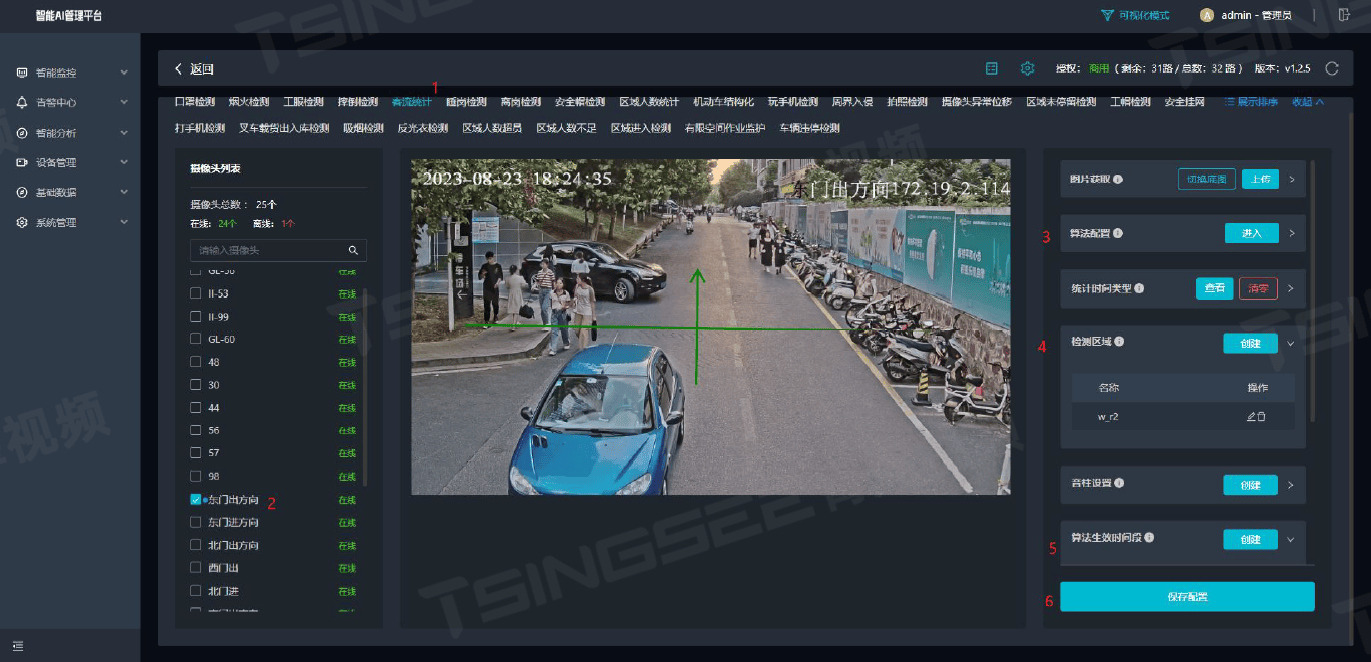
智慧图书馆:构建高效视频智能管理方案,提升图书馆个性化服务
一、背景分析 随着信息技术的飞速发展,智慧图书馆作为现代公共文化服务的重要载体,正逐步从传统的纸质阅读空间向数字化、智能化方向转型。其中,视频智能管理方案作为智慧图书馆安全管理体系的重要组成部分,不仅能够有效提升图书…...

React快速开发框架
本框架主要用于快速搭建项目 使用的基本库:webpackreactreact-routertypescript ps:有不足之处请多多包涵,提出意见或者建议 目的: 前端开发大多数时间是基于市面上比较流行的成品框架开始进行开发,途中遇到的问题大…...

【前端】记录各种控制台警告/bug
一、Element Plus 1、控制台警告:“Runtime directive used on component with non-element root node. The directives will not function as intended.” 错误原因:在 Vue 组件上使用了运行时指令(指那些在运行时动态绑定到 DOM 元素上的指…...

猫咪掉毛严重怎么办?铲屎官家庭必备清理工具——宠物空气净化器
“毛,毛,毛,还是毛!”铲屎官们每天都离不开和猫毛斗智斗勇,家里的每个角落都成了“战场”,掉毛的严重程度超乎想象。有时也在后悔当初怎么不养只无毛猫,而是把毛孩子接了回来,世上没…...

顺序表的实现——数据结构
线性表 文章目录 线性表线性表的定义和基本操作线性表的定义线性表的基本操作 线性表的顺序表示顺序表的定义顺序表的实现——静态分配顺序表的实现——动态分配顺序表的特点 线性表的定义和基本操作 线性表的定义 线性表(Linear List)的定义 线性…...

【模块化】CommonJS,AMD规范,CMD规范,ES6模块化
1. CommonJS Node.js基于CommonJS规范应运而生 1.1 commonjs规范语法导出模块 module.exports { a, b }1.2 commonjs规范语法引入模块 const mod require(./导出模块name)2. AMD 规范 RequireJS 是AMD规范的实现。是js文件和模块的加载器。 在没有单页应用(angu…...

3.js - 顶点着色器、片元着色器的联系
1、定义与功能 顶点着色器 顶点着色器,是图形渲染管线中的第一个可编程阶段,它的主要任务是,处理从CPU发送到GPU的顶点数据,包括:1、顶点位置的变换(如:模型空间 -> 世界空间 -> 视图控件…...

kotlin简介
Kotlin 是一种在 Java 虚拟机上运行的静态类型编程语言,被称之为 Android 世界的Swift,由 JetBrains 设计开发并开源。 Kotlin 可以编译成Java字节码,也可以编译成 JavaScript,方便在没有 JVM 的设备上运行。 在Google I/O 2017…...

Mintegral出海系列:解锁全球应用商店新增长路径
在全球化竞争的浪潮中,面对打法各异的应用和游戏品类,以及全球数百个环境不同的国家和地区,开发者们正面临着前所未有的挑战。Mintegral「出海ing」系列专题内容,助力出海开发者选准赛道探索新的增长路径。 据近期数据显示&#x…...

Qt 哈希加密之 QCryptographicHash
【写在前面】 QCryptographicHash 是 Qt 框架中提供的一个类,它用于实现加密散列函数,也就是我们常说的哈希函数。哈希函数能够将任意长度的数据转换为固定长度的哈希值,这个哈希值通常用于数据的完整性校验、密码存储等场景。 什么是哈希函数…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
