数位DP 详解及其案例实战 [模板+技巧+案例]
零. 案例引入
1.案例引入 leetcode233. 数字 1 的个数
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
输入:n = 13
输出:62.暴力解
对于上述的案例,暴力解肯定是可行的,但时间复杂度较高,对于小于n的所有数字,直接遍历一遍即可
class Solution {public int countDigitOne(int n) {int sum = 0;for(int i = 1; i <= n; i++){sum += countone(i);}return sum;}public int countone(int n){char[] ch = Integer.toString(n).toCharArray();int sum = 0;for(int i = 0; i < ch.length; i++){if(ch[i] == '1'){sum++;}}return sum;}
} 
3.引出数位DP
显然,上述方法肯定是会超时的,稍微数字大一些就会超时,那么对于数字类按位遍历的题目,可以考虑使用数位DP来解决。由于在以下论述中,会返回出现leetcode233. 数字 1 的个数和leetcode1012 至少有 1 位重复的数字 这两道题目,需要提前看题。
一. 数位DP简单介绍
1.数位DP的本质
这里直接给出数位DP的本质:DFS+记忆化搜索(可选项)+约束(可选项)
那么为了更容易理解,还是以leetcode233. 数字 1 的个数为例,对于原题目,我们很容易得到下图中的疑问与结论(以n=123为例,且先不考虑数字1的个数,只是遍历所有可能结果):
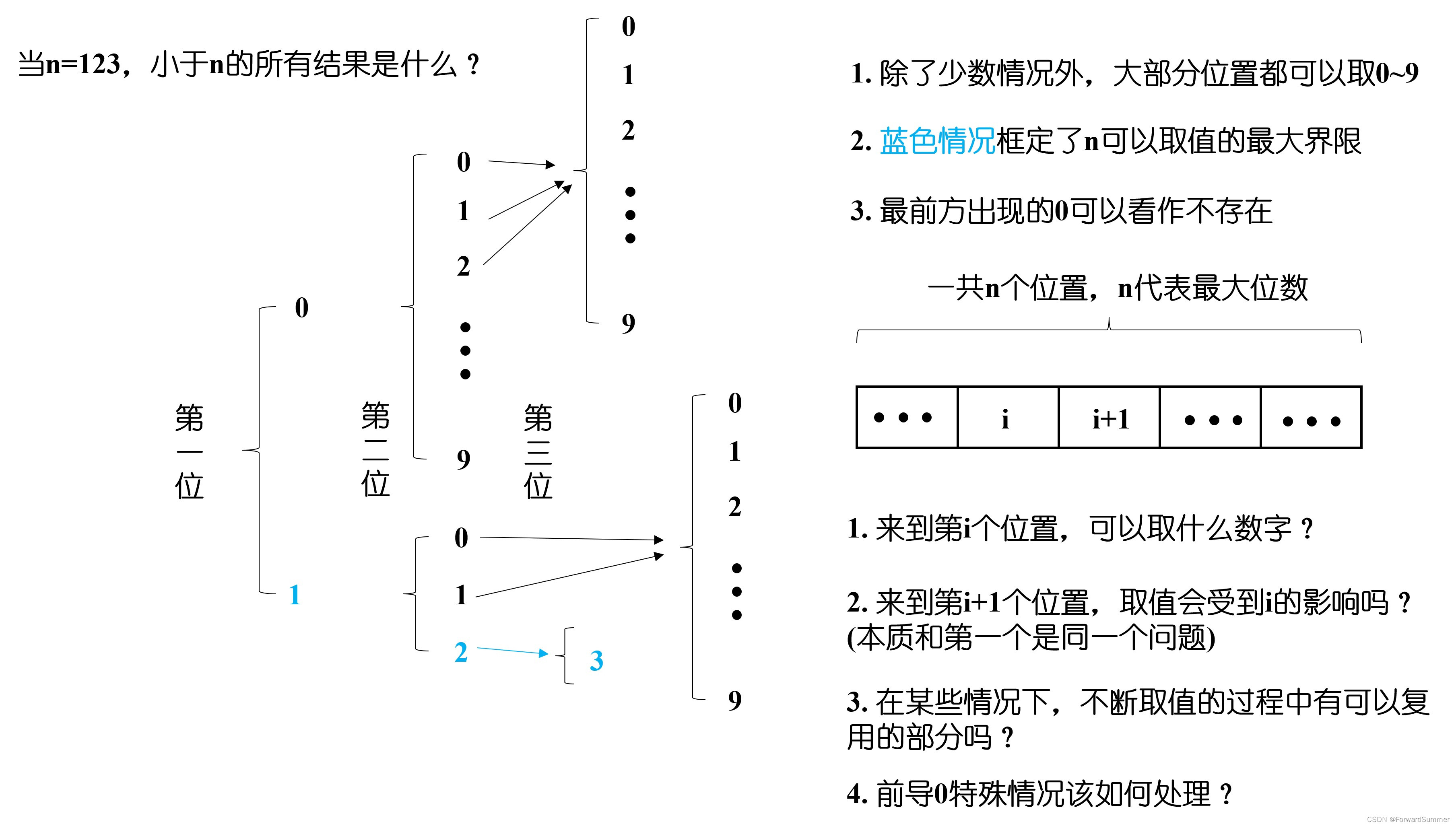
通过观察上图,不难发现:
1. 除了少数情况外,大部分位置都可以取0~9
2. 蓝色情况框定了n可以取值的最大界限
3. 最前方出现的0可以看作不存在(按照题目要求不同,前导0可以不处理)
2.数位DP适合处的问题
(1)数位DP适合处理的典型问题:
Ⅰ. 按位遍历的数字 或者 能组成按位遍历的数字
Ⅱ. 暴力解简单但是数字稍微大一些就超时
Ⅲ. 通常小于某个数的所有合集
(2)为何找规律的方法不建议使用
对于一些题目,找规律进行情况拆解判断当然也是可以的,可以做到更低的时间复杂度和空间复杂度,对于leetcode233. 数字 1 的个数这道题目,极致的找规律方法只需要几行{Ref. [3]}
public int countDigitOne(int n) {int count = 0;for (long k = 1; k <= n; k *= 10) {long r = n / k, m = n % k;count += (r + 8) / 10 * k + (r % 10 == 1 ? m + 1 : 0);}return count;
}
但是在面试笔试中,不管是时间上还是找边界条件和Bug都是不容易的一件事,使用模板更容易解决。
3.数位DP在实际使用面临什么难点
(1) 来到第i个位置,可以取什么数字?
(2)来到第i+1个位置,取值会受到i的影响吗?(本质和第一个是同一个问题)
(3)在某些情况下,不断取值的过程中有可以复用的部分吗?
(4)前导0特殊情况该如何处理?
二. 数位DP典型模板和技巧
1.模板 Ref. [1~2]
class Solution {char s[];int memo[][];public int count(int n) {s = Integer.toString(n).toCharArray();int m = s.length;memo = new int[m][];for (int i = 0; i < m; i++){Arrays.fill(memo[i], -1); } return f(0, 0, 约束条件);}int f(int i, int mask, 约束条件) {if (i == s.length){return int; }if (约束条件 && memo[i][mask] != -1){return memo[i][mask];}int res = 0;int up = 当前数字的上限; for (int d ; d <= up; ++d){res += f(i + 1, new_mask, 新约束条件);}if (约束条件){memo[i][mask] = res;} return res;}
}2.模板解读
(1)初始化的准备
char s[];int memo[][];s = Integer.toString(n).toCharArray();int m = s.length;memo = new int[m][];for (int i = 0; i < m; i++){Arrays.fill(memo[i], -1); } s是对于数字n的字符版本,便于遍历,memo是记忆化搜索的备忘录,刚开始没有任何记录就是-1
(2)主体函数
f(0, 0, 约束条件)f为DFS的主体函数,第一个0代表从第0位开始,第二个0代表mask集合*{Ref.[1]} ,约束条件限制了当前循环的一些步骤,比如是否是底线限制情况,即在n=123时,我们的数字是不能超过123,即是上图中的蓝色情况,换种说法就是按照底限贴着进行深度搜索的。
mask集合*:“集合可用二进制表示,二进制从地位低位到高位可以表示,比如{0,2,3}可以表示为{1101},如果是{0,1,2,3}可表示为{1111},向集合c添加数据d可以表示为 c | (1<<d),即把c的第d位置置1,判断一个数d是否在c中 (c >> d) & 1,若为真则证明在集合中。“
mask集合*:可选选项。
mask集合*:可以判断在当前位置上,要选的数字之前是否选过,比如在题目leetcode1012 至少有 1 位重复的数字 这道题来说,我们去思考相反面,即所有不重复的数字,最后用n-所有不重复的数字就是题目所需要的答案。那么,我们需要选择不重复的数字,那么,我们把已经选择的数字放在一个集合中,后续就不要选择。
(3)深度搜索终止条件
if (i == s.length){return int; }当i来到数字的最后一个位置时,即结束搜索。
(4)记忆化搜索的备忘录部分
if (约束条件 && memo[i][mask] != -1){return memo[i][mask];}if (约束条件){memo[i][mask] = res;} 当命中缓存后,直接返回缓存的值,更新缓存值。
(5)主体按位遍历部分
for (int d ; d <= up; ++d){res += f(i + 1, new_mask, 新约束条件);}在循环中,进行下一位的遍历,所以是i+1,又因为在集合中加入了新的元素,所以把新的元素更新, 此时的约束条件也有可能改变,也需要更新。
如上所述,new_mask是可选部分。
(6)最终结果部分
int res = 0;return res;(7)上限up部分、缓存部分和约束部分(重点)
约束条件
int up = 当前数字的上限; 约束条件和上限部分一起分析,本质都是对数字的约束,缓存又和约束有关联,所以都放在了一起,这一部分是数位DP的难点。
Ⅰ、当未贴限行走,那么数字的上限就是9,贴限行走,上限就是数字对应的那一位
int up = isLimit ? s[i] - '0' : 9;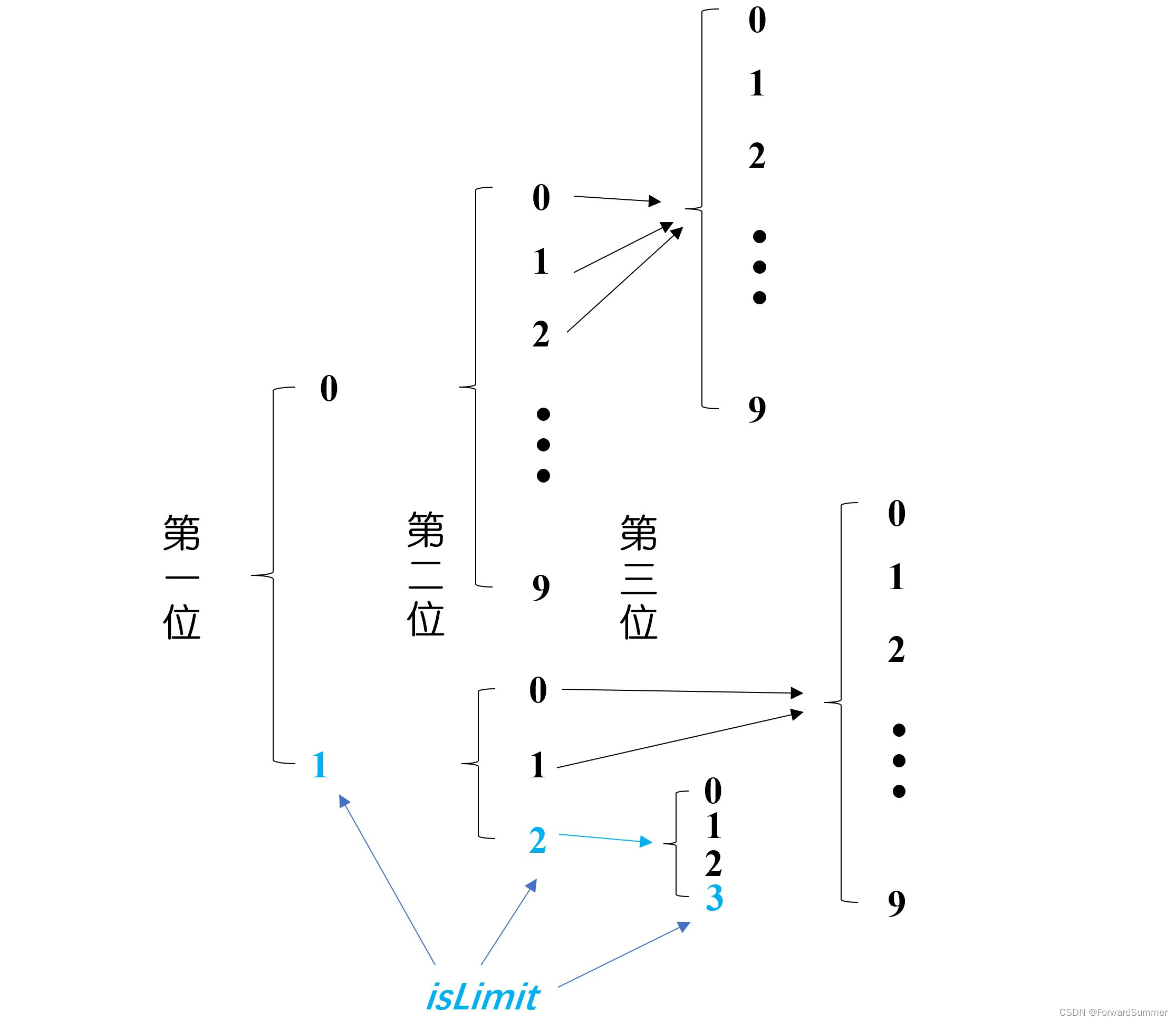
Ⅱ、蓝色限,isLimit,boolean型变量,若为真,则是贴限遍历,即对于n=123来说,前两个位置的元素都选择了和n一样的情况,即当前数为“12x”,x是当前需要选择的数,由于之前一直是贴限取值,那么在当前轮,
int up = s[i];up不能选择超过s[i]的数,否则例如选了个“129”,则超出题目范畴。
Ⅲ、前导0,是会出现的一种特殊情况,在有些题目需要处理,有些则不需要,我们一般用lead,boolean型变量来保存,那么在leetcode233. 数字 1 的个数的题目中,前导0可以不用考虑,因为此时是计算中数字1的个数,前面又多少个0对结果没有影响,我们只是计算1的个数,换言之,题目把要求计算n中1~9任意一个数字的个数都不会有影响。相反,当题目中的要求是计算数字中0的个数,此时开始有影响了,因为如果在第一位取0,那么它是不合法的,因为“012”会计算此时含有一个0,实际上,“012” = “12”,此时是不含有0的。
那么,换一道题目进行阐述,前导0需要考虑的情况,对于题目leetcode1012 至少有 1 位重复的数字 这道题来说,此时的0就应该考虑。
若第一位选择“0”,在后续的可能产生的结果中出现了“0103”,那么0出现了两次,出现了相同的数字二不合法,而正常来说,“0103”在实际意义上起始表示的是“103”,其实是一个符合题目要求的数字,所以综合以上论述,此时需要一个前导0判断位,来判断此时到底是不是符合题目要求。
Ⅳ、缓存和isLimit联动部分。若:
if (isLimit){// memo[i][mask] = res;} 即在蓝色限部分,需要缓存吗,答案是不需要的,蓝色部分只会走一次,不需要进行缓存,不会用到第二次就不用进行缓存。
Ⅴ、mask在主体函数中介绍过,使用的关键在于需不需要对已经选过的数做约束,即像在leetcode1012 至少有 1 位重复的数字。 此题转换成相反的操作后,即n-所有不重复的数字,就需要约束,即出现的数字不要再选。
Ⅵ、缓存memo。对于一个可记忆化递归的函数来说,那么
和
是可以产生相同结果的情况,在缓存
产生,并在第二次,第三次碰见后,可以直接拿来使用。那么对于题目leetcode233. 数字 1 的个数 中,在什么情况下才可以使用备忘录呢?此时对于记忆化方程
来说,我们需要记录走到了第几位,也需要知道当前1的个数,此时的x为集合{i,cntOne},i是来到第几位,cntOne是1的个数,有了这两个部分才能进行缓存,记忆化方程变为
.
Ⅶ、
3.相关技巧总结
(1)isLimit代表贴限判断,判断当前位置可选的最大值。
(2)二进制集合mask中记录已经选择过的数字,在一些题目中会用到。
(3)前导0是个大麻烦,但在有些题目中我们可以选择不处理,在有些题目中当作跳过位标志,以此来决定从0开始还是从1开始。
(4)记忆化搜索可以复用以来减少时间复杂度,但一定注意使用的场合,究竟是不是两个相同情况的,对于leetcode233这种题目,是不是要额外考虑其他的状态。
三. 数位DP典型案例
1.稍微简单 leetcode233 数字 1 的个数
先贴代码
DFS
class Solution {char[] ch;public int countDigitOne(int n) {ch = Integer.toString(n).toCharArray();return f(0, 0, true);}int f(int i, int oneCnt, Boolean isLimit){if(i == ch.length) return oneCnt;int up = isLimit ? ch[i] - '0' : 9;int sum = 0;for(int d = 0; d <= up; d++){sum += f(i+1,oneCnt + (d == 1 ? 1 : 0), isLimit && d == up);}return sum;}
}这种方法会超时

DFS+记忆化搜索
那么加上缓存
class Solution {char[] ch;int[][] memo;public int countDigitOne(int n) {ch = Integer.toString(n).toCharArray();memo = new int[ch.length][ch.length];for(int[] arr : memo){Arrays.fill(arr, -1);}return f(0, 0, true);}int f(int i, int oneCnt, Boolean isLimit){if(i == ch.length) return oneCnt;if(!isLimit && memo[i][oneCnt] != -1) return memo[i][oneCnt];int up = isLimit ? ch[i] - '0' : 9;int sum = 0;for(int d = 0; d <= up; d++){sum += f(i+1,oneCnt + (d == 1 ? 1 : 0), isLimit && d == up);}if(!isLimit) memo[i][oneCnt] = sum;return sum;}
}ok,通过。
逐行讲解
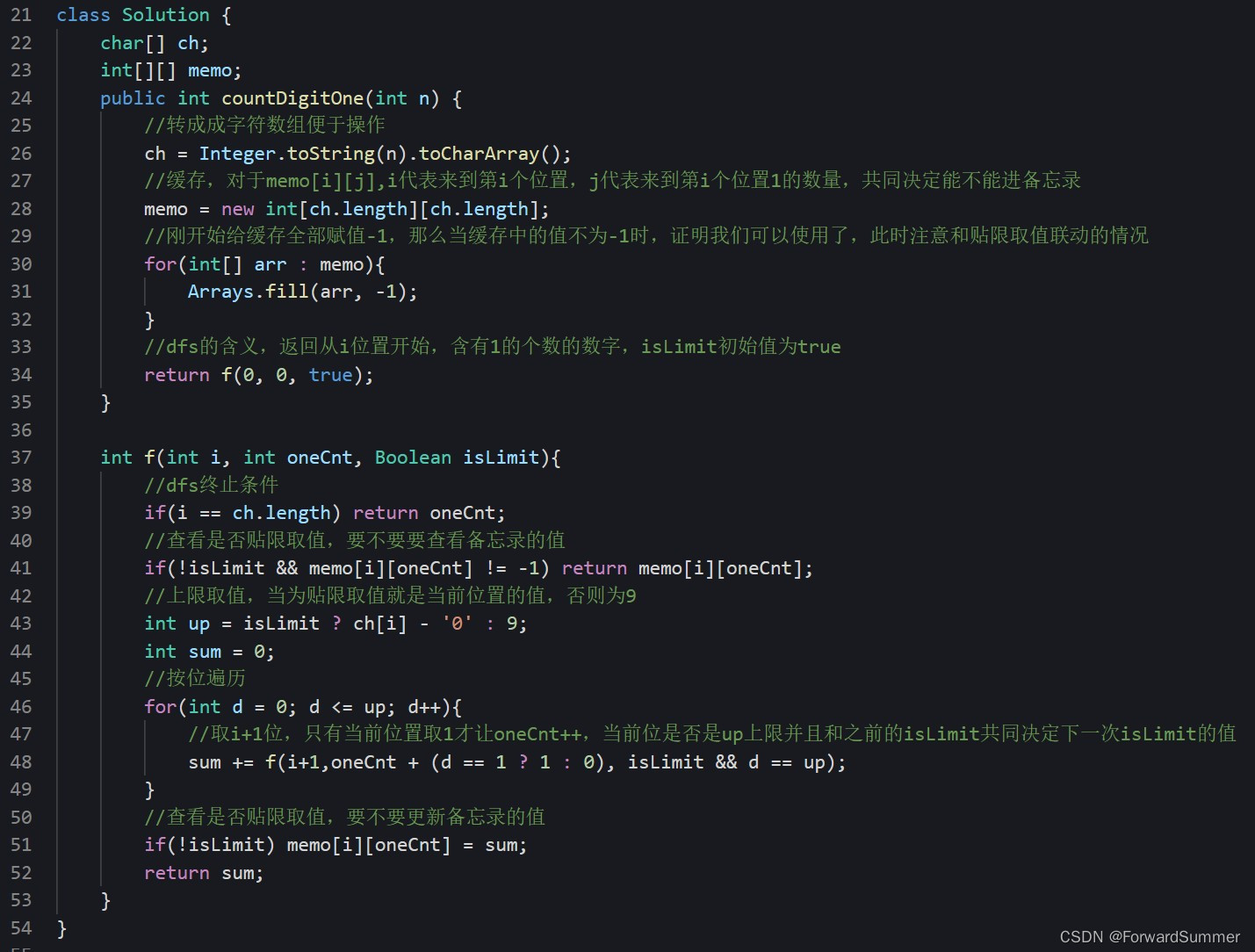
难点剖析:
(1)为何需要两个参数才能确定记忆化方程的唯一确定状态
当我们来到第i位置,我们选择的数字不同会影响结果,比如,选择2,选择9,选择4,都会产生相同的结果,但是,选择1就不一样了,因为选择1会使得当前的结果确确实实增加1,选择其他数字不会。又因为是不是贴限取值(也就是蓝色部分),也会产生不一样的结果,因为在蓝色部分会有限制,导致我们无法取得更高的数字(在n=123时,无法取得126,导致10X和12X中的X会产生不同的结果。)
进一步,根据{Ref.[2]}:
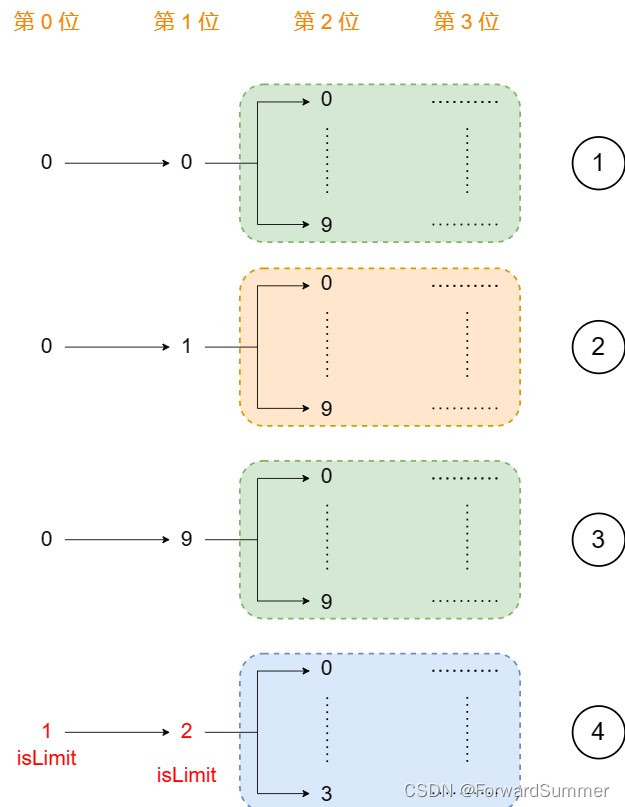
假设第一种情况的结果已经计算出来如果我们处于第三种情况下的第 1 位的时候,思考:后面的部分还需要再次计算吗?显然不需要,因为在第一种情况的时候已经算过了,只要我们将第一种情况计算的结果保存一下即可再次复用
如果我们处于第二种情况下的第 1 位的时候,思考:后面的部分还需要再次计算吗?这次是需要滴!有人可能有疑问了,为啥第三种情况不需要计算,而第二种情况就需要了设绿色部分的结果为 x,如果直接复用,那么第二种情况最终返回的结果为 x,显然有问题呀,因为第二种情况的第 1 位为 1,所以第二种情况的结果应该是 x + 1 才对呀出现这个问题的原因在于:我们不能只通过位数来表示一种状态,还需要根据当前已有 1 数量,即参数 oneCnt,所以我们可以用一个二维数组 memo[][] 来表示所有状态还有最后一个问题,蓝色部分的结果可以复用吗?显然也是不可以的,蓝色部分由于限制的原因,只能选择 0 - 3,状态和上面绿色的部分是不一样的。isLimit 限制至多只会出现 1 次,到时候特判一下即可。(2)为何isLimit会影响记忆化搜索的备忘录
当 当前值处于isLimit状态时,证明为贴蓝限取值,此时的值知会取一次,所以不需要进备忘录。
(3)为何isLimit初始赋值为true
若isLimit初始值为false;那么isLimit && d == up将一直是false,这是不符合实际情况的。
2.不算简单 leetcode 2376 统计特殊整数
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
输入:n = 20
输出:19
解释:1 到 20 之间所有整数除了 11 以外都是特殊整数。所以总共有 19 个特殊整数。代码
class Solution {int[][] memo;//记忆化搜索char[] ch;public int countSpecialNumbers(int n) {ch = Integer.toString(n).toCharArray();int len = ch.length;memo = new int[len][1<<10];//2 * 10^9 所以开10个长度单位for(int i = 0; i < len; i++){Arrays.fill(memo[i],-1);//全是-1当作缓存}//从第0为开始,刚开始的集合为0,return f(0,0,true,false);}//来到第i个位置,mask为集合,存放已经放进去的数字,采用二进制,//isLimit,前面填写的数字是否都是n对应起来的,则当前位置最多为s[i],否则0-9,如135,来到13,那么最后一个位置只能0-5,不饿能超说过5,//isNum,来到第i处我可以选择跳过,什么都不填写,也可以填数字public int f(int i, int mask, Boolean isLimit, Boolean isNum){if(i == ch.length){return isNum ? 1 : 0;//来到最后一个位置,如果是个数九返回1,不是返回0}//击中缓存if(!isLimit && isNum && memo[i][mask] != -1){return memo[i][mask];}int res = 0;//当前位置跳过,跳过肯定不用管上限,mask也未变化,if(!isNum){res = f(i+1,mask,false,false);}//寻找当前值的上界int up = isLimit ? ch[i] - '0' : 9;//开始枚举for(int d = isNum ? 0:1; d <=up; d++){if( ((mask>>d) & 1) == 0 ){res += f(i+1,mask | (1<<d), isLimit && d == up, true);}}//做缓存,当前未对应且当前未跳过if(!isLimit && isNum){memo[i][mask] = res;}return res;}
}难点剖析:
(1)前导0是个大麻烦,在此题中使用isNum标志位来进行判断,当来到第i位:
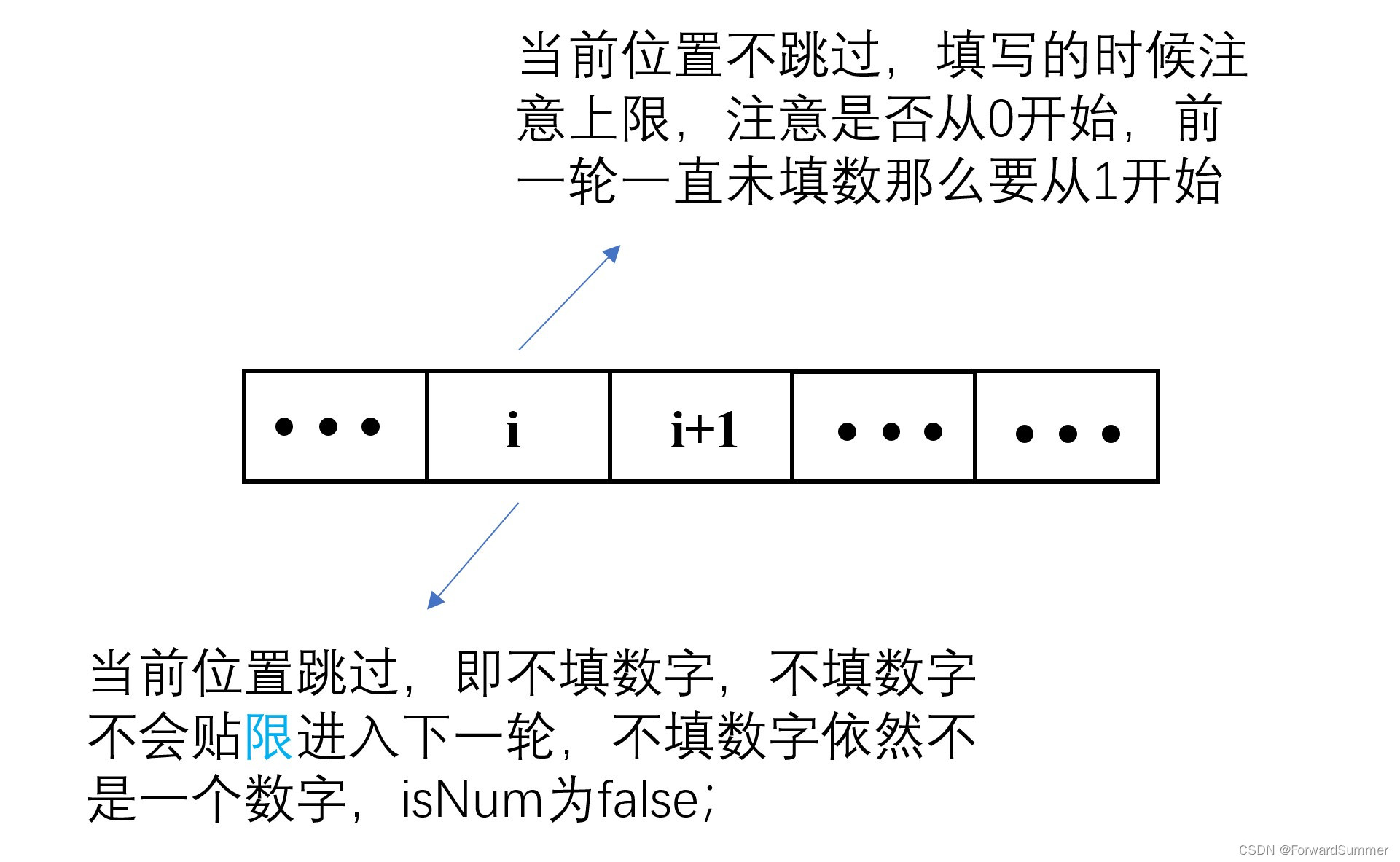
(2)isLimit是true的情况,只会遇到一次,因此不需要记忆化,同样的,isNum是前导0的情况,当作跳过的情况,也不需要记忆化。
(3)来到第i个位置对于,对于当前的位置以及已经取了哪些数字,决定了记忆化搜索的方程,并且是否更新备忘录,当mask中的集合一样时,比如mask:{1,0,0,1}代表int数字9,9包含的元素有{0,3},即在当前的mask中,0和3已经取过了,不能再取了。
3.同一属性 leetcode1012 至少有 1 位重复的数字
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
输入:n = 20
输出:1
解释:具有至少 1 位重复数字的正数(<= 20)只有 11 。答案:
return n-f(0,0,true,false);不再赘述,直接n-f(n),其中n为要求的数字,f()为leetcode 2376的函数。
参考来源Ref:
【1】leetcode 灵茶山艾府 数位 DP 通用模板,附题单(Python/Java/C++/Go)
【2】leetcode LFool 数位 DP 详解「汇总级别整理 🔥🔥🔥」
【3】leetcode windliang 详细通俗的思路分析,多解法
【4】b站 灵茶山艾府 数位 DP 通用模板【力扣周赛 306】LeetCode
相关文章:
数位DP 详解及其案例实战 [模板+技巧+案例]
零. 案例引入 1.案例引入 leetcode233. 数字 1 的个数 给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。 输入:n 13 输出:6 2.暴力解 对于上述的案例,暴力解肯定是可行的,但时间复杂度较高,对…...
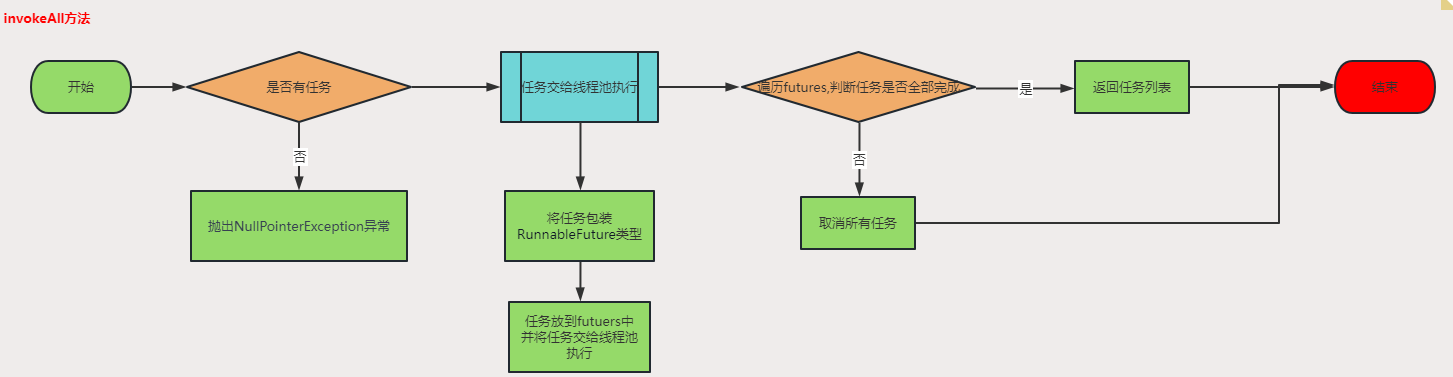
并发编程(六)—AbstractExecutorService源码分析
一、AbstractExecutorService简介AbstractExecutorService是一个抽象类,实现了ExecutorService接口,提供了线程池的基本实现。它是Java Executor框架的核心类,提供了线程池的基本操作,如提交任务、管理线程池、执行任务等。自定义…...

015行为型-职责链模式
目录定义标准模式实现:职责链变体使用链表实现使用数组实现应用场景日志输出spring过滤器spirng 拦截器mybatis动态sql定义 责链模式是一种设计模式,其目的是使多个对象能够处理同一请求,但是并不知道下一个处理请求的对象是谁。它能够解耦请…...
python例程:五子棋(控制台版)程序
目录《五子棋(控制台版)》程序使用说明程序示例代码可执行程序及源码下载路径《五子棋(控制台版)》程序使用说明 在PyCharm中运行《五子棋(控制台版)》即可进入如图1所示的系统主界面。 图1 游戏主界面 具…...

leveldb的Compaction线程
个人随笔 (Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 1. leveldb的Compaction全局线程 在leveldb中,有一个全局的后台线程BGThread,用于数据库的MinorCompact与MajorCompact。 重点关注“全局线程”: 这个标识着无论一个进程打开…...

邪恶的想法冒出,立马启动python实现美女通通下
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 完整源码、python资料: 点击此处跳转文末名片获取 当我在首页刷到这些的时候~ 我的心里逐渐浮现一个邪念:我把这些小姐姐全都采集,可以嘛? 答案当然是可以的~毕竟就我这技术,…...

蓝桥杯刷题冲刺 | 倒计时18天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录0.知识点1.乳草的入侵今天写 搜索题 0.知识点 DFS 设计步骤 确定该题目的状态(包括边…...

经典算法面试题——Java篇-附带赠书活动,评论区随机选取一人赠书
目录 一.图书推荐 二.说一下什么是二分法?使用二分法时需要注意什么?如何用代码实现? 三.什么是插入排序?用代码如何实现? 四.什么是冒泡排序?用代码如何实现? 五.什么是斐波那契数列&#…...

支持RT-Thread最新版本的瑞萨RA2E1开发板终于要大展身手了
支持RT-Thread最新版本的瑞萨RA2E1开发板终于要大展身手了 熟悉RT-Thread和瑞萨MCU的朋友都知道,当前RT-Thread仓库的主线代码是不支持RA2E1这个BSP的。刚好,最近我在联合瑞萨推广一个叫《致敬未来的攻城狮计划》,使用的就是RA2E1开发板&…...

【C语言进阶】 12. 假期测评①
day01 1. 转义字符的判断 以下不正确的定义语句是( ) A: double x[5] {2.0, 4.0, 6.0, 8.0, 10.0}; B: char c2[] {‘\x10’, ‘\xa’, ‘\8’}; C: char c1[] {‘1’,‘2’,‘3’,‘4’,‘5’}; D: int y[53]{0, 1, 3, 5, 7, 9}; 【答案解析】 B 本…...
给程序加个进度条吧,1行Python代码,快速添加~
大家好,这里是程序员晚枫。 你在写代码的过程中,有没有遇到过以下问题? 已经写好的程序,想看看程序执行的进度? 在写代码批量处理文件的时候,如何显示现在处理到第几个文件了? 👆…...

常见的Keil5编译报错及其原因和解决方法
以下是几种常见的Keil5编译报错及其原因和解决方法: "Error: L6218E: Undefined symbol"(未定义符号错误) 这通常是由于缺少对应的库文件或者代码中有未声明的变量或函数引起的。解决方法是检查相应的库文件是否已正确添加到工程中…...
Django 实现瀑布流
需求分析 现在是 "图片为王"的时代,在浏览一些网站时,经常会看到类似于这种满屏都是图片。图片大小不一,却按空间排列,就这是瀑布流布局。 以瀑布流形式布局,从数据库中取出图片每次取出等量(7 …...
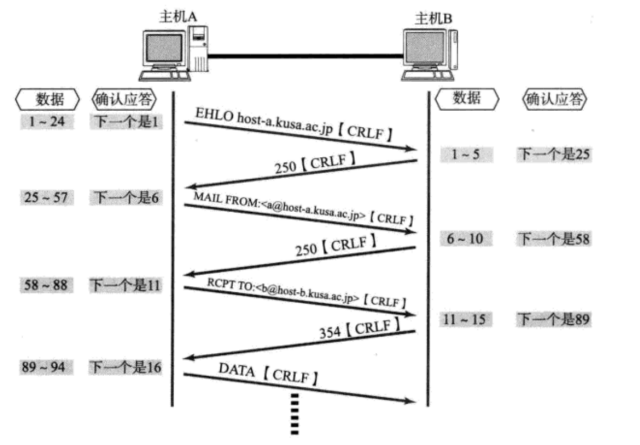
传输层协议----UDP/TCP
文章目录前言一、再谈端口号端口号的划分认识知名端口号(Well-Know Port Number)两个问题nestatpidof二、UDP协议UDP协议端格式UDP的特点面向数据报UDP的缓冲区UDP使用注意事项基于UDP的应用层协议二、TCP协议TCP协议段格式可靠性问题确认应答(ACK)机制流量控制六个标志位PSHUG…...

教你如何快速在Linux中找到某个目录中最大的文件
工作中经常会有查看某个目录下最大的文件的需求,比如在运维工作中,发现某个系统或功能不工作了,经排查发现是服务器空间满了…那么接下来就需要清理一下临时文件或者日志文件,或者其他不需要的文件,那么就会想要查看一…...

Java二叉树面试题讲解
Java二叉树面试题讲解🚗1.检查两颗树是否相同🚕2.另一颗树的子树🚙3.二叉树最大深度🚌4.判断一颗二叉树是否是平衡二叉树🚎5.对称二叉树🚓6.获取树中结点个数🚑7.判断一个树是不是完全二叉树&am…...

rancher2.6进阶之nfs动态创建pv配置
添加NFS client provisioner 动态提供K8s后端存储卷 1.1.前提说明 1.1.1.说明 NFS client provisioner 利用 NFS Server 给 Kubernetes 作为持久存储的后端,并且动态提供PV。 默认 rancher 2 的存储类中的提供者不包含NFS,需要手动添加;添加方式有两种: 1)从应用商店直接安…...
快速上手vue elementUI好看的登录界面
这是一个非常非常适合新手的vue登录界面,总体来说美观大气,axios那部分没有发,有需要的大家可以自己进行二次开发,继续编写。 用到了技术栈有 vue/cli 5.07 element-ui 2.15.9 适合入门级新手,展示下页面 emmm验证码…...
Vue趣味【Vue3+Element Plus+Canvas实现一个简易画板;支持导出为图片】
目录🌟前言🌟粉丝先看🌟创建Vue3项目🌟引入Element Plus🌟实现代码(详细注释)🌟写在最后🌟JSON包里写函数,关注博主不迷路🌟前言 哈喽小伙伴们&a…...
【Spring Cloud Alibaba】2.服务注册与发现(Nacos安装)
文章目录环境要求简介安装Nacos源码安装Docker安装数据库配置访问服务我们要搭建一个Spring Cloud Alibaba项目就绕不开Nacos,阿里巴巴提供的Nacos组件,可以提供服务注册与发现和分布式配置服务,拥有着淘宝双十一十几年的流量经验,…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
