经典算法面试题——Java篇-附带赠书活动,评论区随机选取一人赠书
目录
一.图书推荐
二.说一下什么是二分法?使用二分法时需要注意什么?如何用代码实现?
三.什么是插入排序?用代码如何实现?
四.什么是冒泡排序?用代码如何实现?
五.什么是斐波那契数列?用代码如何实现?
一.图书推荐(评论区随机抽奖,送书呦)
今天给大家推荐一本《uni-app跨平台开发与应用从入门到实践》
本书以“零基础”为起点,系统地介绍了uni-app的跨平台开发与应用。全书内容分为3篇,共12章,具体安排如下。
第一篇:基础篇,包括第1~4章,主要介绍了uni-app的特点和优势、环境搭建、HBuilderX开发工具的安装和使用,以及uni-app的一些基础知识。第二篇:进阶篇,包括第5~9章,主要介绍了uni-app的基础配置、相关组件、导航栏、高效开发技巧,以及uniCloud云开发平台。第三篇:实战篇,包括第10~12章,通过第一个实战,介绍了如何使用uni-app开发小程序;通过第二个实战,介绍了如何使用uni-app进行跨平台开发;通过第三个实战,介绍了如何使用uniCloud云开发。
个人感觉:是一本很不错的书籍,适合初学者。感兴趣的点击跳转了解:《uni-app跨平台开发与应用从入门到实践 DCloud/uni-app官方认证教材》(欧阳江涛)【摘要 书评 试读】- 京东图书

二.说一下什么是二分法?使用二分法时需要注意什么?如何用代码实现?
二分法查找(Binary Search)也称折半查找,是指当每次查询时,将数据分为前后两部分,再用中值和待搜索的值进行比较,如果搜索的值大于中值,则使用同样的方式(二分法)向后搜索,反之则向前搜索,直到搜索结束为止。
二分法使用的时候需要注意:二分法只适用于有序的数据,也就是说,数据必须是从小到大,或是从大到小排序的。
public class Lesson7_4 {public static void main(String[] args) {// 二分法查找int[] binaryNums = {1, 6, 15, 18, 27, 50};int findValue = 27;int binaryResult = binarySearch(binaryNums, 0, binaryNums.length - 1, findValue);System.out.println("元素第一次出现的位置(从0开始):" + binaryResult);}/*** 二分查找,返回该值第一次出现的位置(下标从 0 开始)* @param nums 查询数组* @param start 开始下标* @param end 结束下标* @param findValue 要查找的值* @return int*/private static int binarySearch(int[] nums, int start, int end, int findValue) {if (start <= end) {// 中间位置int middle = (start + end) / 2;// 中间的值int middleValue = nums[middle];if (findValue == middleValue) {// 等于中值直接返回return middle;} else if (findValue < middleValue) {// 小于中值,在中值之前的数据中查找return binarySearch(nums, start, middle - 1, findValue);} else {// 大于中值,在中值之后的数据中查找return binarySearch(nums, middle + 1, end, findValue);}}return -1;}
}执行结果如下:
元素第一次出现的位置(从0开始):4
三.什么是插入排序?用代码如何实现?
插入排序(Insertion Sort)算法是指依次把当前循环的元素,通过对比插入到合适位置的排序算法。 比如,下面是一组数据使用插入排序的执行流程:
- 初始化数据:18, 1, 6, 27, 15
- 第一次排序:1, 18, 6, 27, 15
- 第二次排序:1, 6, 18, 27, 15
- 第三次排序:1, 6, 18, 27, 15
- 第四次排序:1, 6, 15, 18, 27
插入排序算法代码实现,如下所示:
public class Lesson7_4 {public static void main(String[] args) {// 插入排序调用int[] insertNums = {18, 1, 6, 27, 15};System.out.println("排序前:" + Arrays.toString(insertNums));insertSort(insertNums);System.out.println("排序后:" + Arrays.toString(insertNums));}/*** 插入排序*/private static void insertSort(int[] nums) {int i, j, k;for (i = 1; i < nums.length; i++) {k = nums[i];j = i - 1;// 对 i 之前的数据,给当前元素找到合适的位置while (j >= 0 && k < nums[j]) {nums[j + 1] = nums[j];// j-- 继续往前寻找j--;}nums[j + 1] = k;System.out.print("第" + i + "次排序:");System.out.println(Arrays.toString(nums));}}
}执行结果如下:
排序前:[18, 1, 6, 27, 15]
第1次排序:[1, 18, 6, 27, 15]
第2次排序:[1, 6, 18, 27, 15]
第3次排序:[1, 6, 18, 27, 15]
第4次排序:[1, 6, 15, 18, 27]
排序后:[1, 6, 15, 18, 27]
四.什么是冒泡排序?用代码如何实现?
冒泡排序(Bubble Sort)算法是所有排序算法中最简单、最基础的一个,它的实现思路是通过相邻数据的交换达到排序的目的。
冒泡排序的执行流程是:
- 对数组中相邻的数据,依次进行比较;
- 如果前面的数据大于后面的数据,则把前面的数据交换到后面。经过一轮比较之后,就能把数组中最大的数据排到数组的最后面了;
- 再用同样的方法,把剩下的数据逐个进行比较排序,最后得到就是从小到大排序好的数据。
冒泡排序算法代码实现,如下所示:
public class Lesson7_4 {public static void main(String[] args) {// 冒泡排序调用int[] bubbleNums = {132, 110, 122, 90, 50};System.out.println("排序前:" + Arrays.toString(bubbleNums));bubbleSort(bubbleNums);System.out.println("排序后:" + Arrays.toString(bubbleNums));}/*** 冒泡排序*/private static void bubbleSort(int[] nums) {int temp;for (int i = 1; i < nums.length; i++) {for (int j = 0; j < nums.length - i; j++) {if (nums[j] > nums[j + 1]) {temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}System.out.print("第" + i + "次排序:");System.out.println(Arrays.toString(nums));}}
}
执行结果如下:
排序前:[132, 110, 122, 90, 50]
第1次排序:[110, 122, 90, 50, 132]
第2次排序:[110, 90, 50, 122, 132]
第3次排序:[90, 50, 110, 122, 132]
第4次排序:[50, 90, 110, 122, 132]
排序后:[50, 90, 110, 122, 132]
五.什么是斐波那契数列?用代码如何实现?
斐波那契数列(Fibonacci Sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711...... 在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用。
斐波那契数列之所以又称黄金分割数列,是因为随着数列项数的增加,前一项与后一项之比越来越逼近黄金分割的数值 0.6180339887......
斐波那契数列指的是这样一个数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711......
斐波那契数列的特征 :第三项开始(含第三项)它的值等于前两项之和。
斐波那契数列代码实现示例,如下所示:
public class Lesson7_4 {public static void main(String[] args) {// 斐波那契数列int fibonacciIndex = 7;int fibonacciResult = fibonacci(fibonacciIndex);System.out.println("下标(从0开始)" + fibonacciIndex + "的值为:" + fibonacciResult);}/*** 斐波那契数列* @param index 斐波那契数列的下标(从0开始)* @return int*/private static int fibonacci(int index) {if (index == 0 || index == 1) {return index;} else {return fibonacci(index - 1) + fibonacci(index - 2);}}
}
执行结果如下:
下标(从0开始)7的值为:13
相关文章:

经典算法面试题——Java篇-附带赠书活动,评论区随机选取一人赠书
目录 一.图书推荐 二.说一下什么是二分法?使用二分法时需要注意什么?如何用代码实现? 三.什么是插入排序?用代码如何实现? 四.什么是冒泡排序?用代码如何实现? 五.什么是斐波那契数列&#…...

支持RT-Thread最新版本的瑞萨RA2E1开发板终于要大展身手了
支持RT-Thread最新版本的瑞萨RA2E1开发板终于要大展身手了 熟悉RT-Thread和瑞萨MCU的朋友都知道,当前RT-Thread仓库的主线代码是不支持RA2E1这个BSP的。刚好,最近我在联合瑞萨推广一个叫《致敬未来的攻城狮计划》,使用的就是RA2E1开发板&…...

【C语言进阶】 12. 假期测评①
day01 1. 转义字符的判断 以下不正确的定义语句是( ) A: double x[5] {2.0, 4.0, 6.0, 8.0, 10.0}; B: char c2[] {‘\x10’, ‘\xa’, ‘\8’}; C: char c1[] {‘1’,‘2’,‘3’,‘4’,‘5’}; D: int y[53]{0, 1, 3, 5, 7, 9}; 【答案解析】 B 本…...
给程序加个进度条吧,1行Python代码,快速添加~
大家好,这里是程序员晚枫。 你在写代码的过程中,有没有遇到过以下问题? 已经写好的程序,想看看程序执行的进度? 在写代码批量处理文件的时候,如何显示现在处理到第几个文件了? 👆…...

常见的Keil5编译报错及其原因和解决方法
以下是几种常见的Keil5编译报错及其原因和解决方法: "Error: L6218E: Undefined symbol"(未定义符号错误) 这通常是由于缺少对应的库文件或者代码中有未声明的变量或函数引起的。解决方法是检查相应的库文件是否已正确添加到工程中…...
Django 实现瀑布流
需求分析 现在是 "图片为王"的时代,在浏览一些网站时,经常会看到类似于这种满屏都是图片。图片大小不一,却按空间排列,就这是瀑布流布局。 以瀑布流形式布局,从数据库中取出图片每次取出等量(7 …...
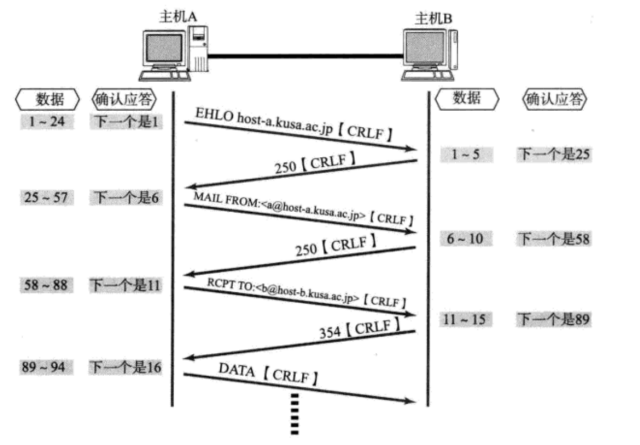
传输层协议----UDP/TCP
文章目录前言一、再谈端口号端口号的划分认识知名端口号(Well-Know Port Number)两个问题nestatpidof二、UDP协议UDP协议端格式UDP的特点面向数据报UDP的缓冲区UDP使用注意事项基于UDP的应用层协议二、TCP协议TCP协议段格式可靠性问题确认应答(ACK)机制流量控制六个标志位PSHUG…...

教你如何快速在Linux中找到某个目录中最大的文件
工作中经常会有查看某个目录下最大的文件的需求,比如在运维工作中,发现某个系统或功能不工作了,经排查发现是服务器空间满了…那么接下来就需要清理一下临时文件或者日志文件,或者其他不需要的文件,那么就会想要查看一…...

Java二叉树面试题讲解
Java二叉树面试题讲解🚗1.检查两颗树是否相同🚕2.另一颗树的子树🚙3.二叉树最大深度🚌4.判断一颗二叉树是否是平衡二叉树🚎5.对称二叉树🚓6.获取树中结点个数🚑7.判断一个树是不是完全二叉树&am…...

rancher2.6进阶之nfs动态创建pv配置
添加NFS client provisioner 动态提供K8s后端存储卷 1.1.前提说明 1.1.1.说明 NFS client provisioner 利用 NFS Server 给 Kubernetes 作为持久存储的后端,并且动态提供PV。 默认 rancher 2 的存储类中的提供者不包含NFS,需要手动添加;添加方式有两种: 1)从应用商店直接安…...
快速上手vue elementUI好看的登录界面
这是一个非常非常适合新手的vue登录界面,总体来说美观大气,axios那部分没有发,有需要的大家可以自己进行二次开发,继续编写。 用到了技术栈有 vue/cli 5.07 element-ui 2.15.9 适合入门级新手,展示下页面 emmm验证码…...
Vue趣味【Vue3+Element Plus+Canvas实现一个简易画板;支持导出为图片】
目录🌟前言🌟粉丝先看🌟创建Vue3项目🌟引入Element Plus🌟实现代码(详细注释)🌟写在最后🌟JSON包里写函数,关注博主不迷路🌟前言 哈喽小伙伴们&a…...
【Spring Cloud Alibaba】2.服务注册与发现(Nacos安装)
文章目录环境要求简介安装Nacos源码安装Docker安装数据库配置访问服务我们要搭建一个Spring Cloud Alibaba项目就绕不开Nacos,阿里巴巴提供的Nacos组件,可以提供服务注册与发现和分布式配置服务,拥有着淘宝双十一十几年的流量经验,…...

深度学习 Day28——利用Pytorch实现好莱坞明星识别
深度学习 Day28——利用Pytorch实现好莱坞明星识别 文章目录深度学习 Day28——利用Pytorch实现好莱坞明星识别一、前言二、我的环境三、前期工作1、导入依赖项设置GPU2、导入数据集3、划分数据集四、调用官方的VGG16模型五、训练模型1、编写训练函数2、编写测试函数3、设置动态…...

Android中使用FCM进行消息推送
Firebase Cloud Message 的介绍 Firebase Cloud Message(FCM)是由Google推出的一种云端消息推送服务,它是由Google推出的Google Cloud Messaging(GCM)服务的升级版。在2016年5月,Google宣布将Google Cloud Messaging重命名为Firebase Cloud Message,作为Firebase的一部…...
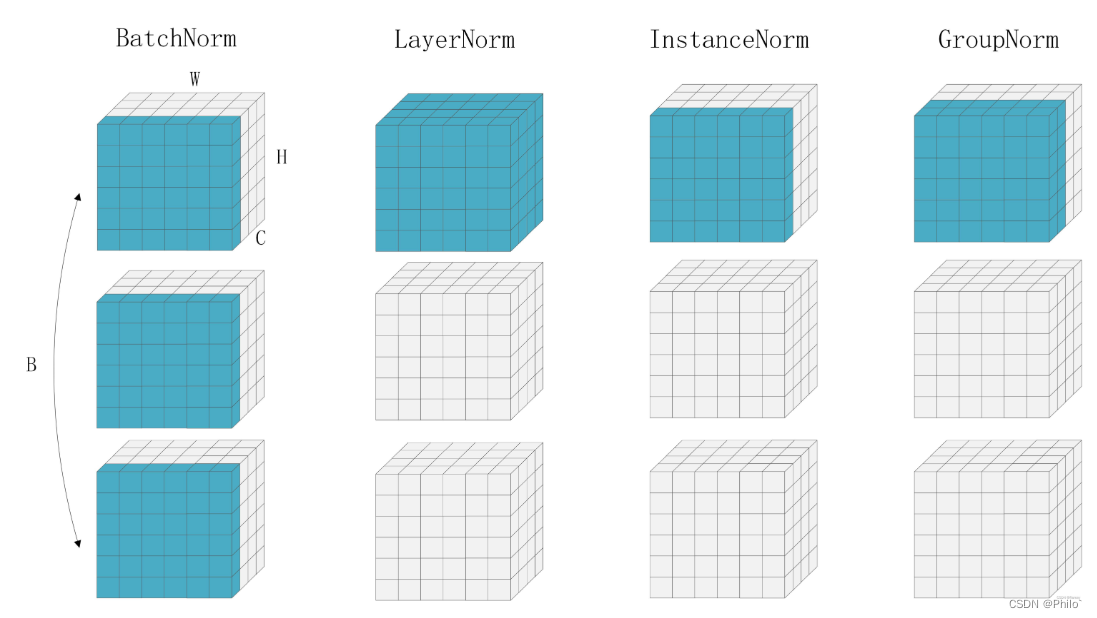
从 X 入门Pytorch——BN、LN、IN、GN 四种归一化层的代码使用和原理
Pytorch中四种归一化层的原理和代码使用前言1 Batch Normalization(2015年提出)Pytorch官网解释原理Pytorch代码示例2 Layer Normalization(2016年提出)Pytorch官网解释原理Pytorch代码示例3 Instance Normalization(2…...

Windows环境下实施域名访问的一些小知识
文章目录 前言一、windows域名访问流程二、网络域名访问配置设置DNS未正确设置DNS的结果三、本地hosts设置本地hosts本地hosts的优先机制本地hosts的内部访问次序示例一示例二总结前言 作为一种常见的操作系统,windows系统具有其特殊的域名访问管理机制。了解其访问机制,将有…...

78.qt QCustomPlot介绍
参考https://www.qcustomplot.com/index.php/tutorials/settingup 下载地址: https://www.qcustomplot.com/index.php/download 1.添加帮助文档 在QtCreator ——>工具——>选项——>帮助——>文档——>添加,选择qcustomplot.qch文件,确定,以后按F1就能跳转到…...
win32api之文件系统管理(七)
什么是文件系统 文件系统是一种用于管理计算机存储设备上文件和目录的机制。文件系统为文件和目录分配磁盘空间,管理文件和目录的存储和检索,以及提供对它们的访问和共享,以下是常见的两种文件系统: NTFSFAT32磁盘分区容量2T32G…...

点云规则格网化,且保存原始的点云索引
点云规则格网化,且保存原始的点云索引 点云深度学习Voxelize规则,参考PTV2:https://github.com/Gofinge/PointTransformerV2 1总执行文件 import numpy as np import torch from pcr.utils.registry import Registry TRANSFORMS Registry…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
