机器学习中的距离概念

距离在机器学习中应用广泛，包括欧式距离、曼哈顿距离、内积距离和KL距离。
下面总结一下。

欧式距离

欧式距离（Euclidean Distance）是机器学习和数据科学中常用的一种距离度量方式，用来衡量两个点在欧几里得空间中的距离。它是通过计算这两个点之间的直线距离来表示的。

应用场景：

• 分类问题：在 k-近邻算法 (k-Nearest Neighbors, KNN) 中，欧式距离被用来衡量待分类样本与已知类别样本之间的距离，以此来判断待分类样本的类别。
• 聚类分析：在聚类算法（如 K-Means）中，欧式距离常用于计算每个样本点与簇中心的距离，从而决定样本点属于哪个簇。
• 降维与度量学习：在某些降维技术（如主成分分析，PCA）或度量学习算法中，欧式距离被用来保持数据点之间的相对距离关系。

特点和局限性：

• 优点：欧式距离直观且易于计算，适用于大多数的物理空间距离计算。
• 局限性：在高维空间（即“维度灾难”）下，欧式距离可能会失去其有效性，因为所有点之间的距离趋向于相似，导致算法效果下降。
• 另外，欧式距离对数据中的尺度敏感，如果各个维度的量纲不同，通常需要进行归一化处理。

曼哈顿距离

曼哈顿距离（Manhattan Distance），也称为城市街区距离（City Block Distance）或 L1 距离，是一种用于度量两个点之间距离的方式。与欧式距离不同，曼哈顿距离表示在一个网格状路径上移动的距离，就像在城市街道中沿着直角走动。

应用场景:

• 分类和回归：在一些机器学习算法中（如 k-近邻算法），曼哈顿距离可以用于衡量样本之间的相似性，尤其是在特征独立且均匀分布的情况下。
• 图像处理：在图像处理中，曼哈顿距离有时用于计算像素之间的距离，因为它能够更好地保持图像的结构特性。
• 神经网络：在某些神经网络的正则化过程中（如 L1 正则化），曼哈顿距离的概念用于惩罚模型的复杂度。

特点和局限性:

• 优点：曼哈顿距离对于高维数据和稀疏数据表现较好，因为它不受高维空间中距离趋同效应的影响。
• 局限性：在某些情况下，曼哈顿距离可能不如欧式距离直观，尤其是当数据更接近连续变化而非离散变化时。

内积距离

内积距离（Inner Product Distance）是一种基于向量内积的相似性度量方法。在机器学习和数据分析中，内积（也称为点积或标量积）通常用于评估两个向量之间的相似性。

应用场景：

• 相似性度量：内积可以用于衡量两个向量之间的相似性。☆在某些推荐系统中，内积用于计算用户与物品之间的相似性。
• 神经网络：在神经网络中，内积是计算神经元输入和权重的线性组合的基础操作。
• 信息检索：在文本检索中，内积可以用于衡量文档与查询向量之间的相似性。

局限性

• 不对称性：内积不是严格意义上的“距离”度量，因为它不满足对称性和三角不等式等性质。
• 尺度问题：由于内积受向量长度影响，直接使用内积作为距离度量可能导致误导性的结果，尤其是在向量长度差异较大的情况下。

为了克服这些局限性，内积通常与其他方法结合使用，如余弦相似性（通过将向量归一化）等。

KL距离

KL距离通常指的是Kullback-Leibler散度（Kullback-Leibler Divergence），又称KL散度或相对熵。它是信息论中用于衡量两个概率分布之间差异的一种非对称度量。KL散度在机器学习、统计学和信息论中有广泛的应用。

注：
KL距离不具有对称性。

应用场景

• 机器学习：在机器学习中，KL散度常用于优化问题，如变分自动编码器（VAE）中，KL散度用于衡量近似后验分布与真实后验分布之间的差异。
• 统计推断：KL散度可用于模型选择和假设检验，通过比较不同模型的拟合优度来选择最合适的模型。
• 信息论：在信息论中，KL散度用于量化两个概率分布之间的差异，特别是在压缩和传输信息时。

距离作为损失函数(MSE/MAE…)

这里补充一下关于内积相似度。如果计算的话，首先需要给出“相似”的定义。
比如下面这个例子。

欧式距离与内积距离的联系

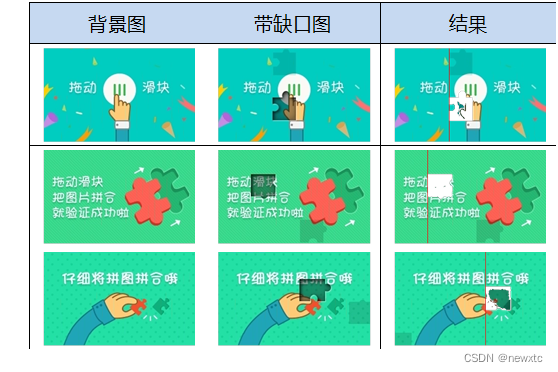
若是在A,B两点到原点的距离都是1的情况下，欧氏距离越大，内积相似度越小。

☆距离的有效性

在机器学习中无论什么距离，都是对短途有效！
距离在过远时已经丧失了意义。

在如上图这种情况下，如果计算A,B之间的距离，不能直接根据A,B两点的坐标进行计算，因为A,B距离“太远”，不能直接计算，而需要找到距离A的很近的若干点，不断地沿着路径计算出d1,d2,d3,…,dn,然后相加即可。