微分方程(Blanchard Differential Equations 4th)中文版Section1.4
1.4 NUMERICAL TECHNIQUE: EULER’S METHOD
上一节中讨论的斜率场的几何概念与近似微分方程解的基本数值方法密切相关。给定一个初值问题
d y d t = f ( t , y ) , y ( t 0 ) = y 0 , \frac{dy}{dt}=f(t,y), \quad y(t_0) = y_0, dtdy=f(t,y),y(t0)=y0,
我们可以通过首先在 t y − ty- ty−平面上绘制斜率,然后从初始值 ( t 0 , y 0 ) (t_0,y_0) (t0,y0) 开始,通过绘制与斜率相切的图形来绘制解决方案的图形。沿着图形的每个点。在本节中,我们描述了一个自动化这个想法的数值过程。使用计算机或计算器,我们可以获得数字和图形,这些数字和图形可以近似解决初始值问题。
数值方法提供了关于解的定量信息,即使我们不能发现它们的公式。还有一个优点是大部分工作可以由机器完成。缺点是我们只能获得近似值,而不是精确解。如果我们仍然意识到这一事实并谨慎行事,那么数值方法将成为研究微分方程的强大工具。即使有可能找到解决方案的公式,也经常使用数值方法。(即使有公式,本文中的大多数微分方程解的图都是使用数值逼近绘制的。)
我们在本节中讨论的数值技术称为欧拉方法。关于欧拉方法以及其他数值方法的精度的更详细讨论将在第7章中给出。
沿斜率场逐步推进过程
为了描述欧拉方法,我们从初值问题开始
d y d t = f ( t , y ) , y ( t 0 ) = y 0 , \frac{dy}{dt}=f(t,y), \quad y(t_0) = y_0, dtdy=f(t,y),y(t0)=y0,
既然我们给定了 f ( t , y ) f (t,y) f(t,y),我们就可以在 t − y t-y t−y 平面上绘制它的斜率。该方法的想法是从斜坡场的点 ( t 0 , y 0 ) (t_0,y_0) (t0,y0) 开始,并采取由斜坡场的切线决定的微小步骤。我们首先选择一个 (小) 步长 Δ t \Delta t Δt。近似解的斜率每 Δ t \Delta t Δt 个单位更新一次。换句话说,对于每一步,我们沿着 t t t 轴移动 Δ t \Delta t Δt 个单位。
从 ( t 0 , y 0 ) (t_0, y_0) (t0,y0) 开始,我们的第一步是到达点 ( t 1 , y 1 ) (t_1, y_1) (t1,y1),其中 t 1 = t 0 + Δ t t_1 = t_0 + \Delta t t1=t0+Δt,并且 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 是通过 ( t 0 , y 0 ) (t_0, y_0) (t0,y0) 的直线上的点,其斜率由 ( t 0 , y 0 ) (t_0, y_0) (t0,y0) 的斜率场给出(见图1.31)。在 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 处,我们重复这一过程。沿着 t t t 轴的步长为 Δ t \Delta t Δt,其方向由 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 的斜率场确定,我们到达新点 ( t 2 , y 2 ) (t_2, y_2) (t2,y2)。新时间由 t 2 = t 1 + Δ t t_2 = t_1 + \Delta t t2=t1+Δt 给出, ( t 2 , y 2 ) (t_2, y_2) (t2,y2) 位于从 ( t 1 , y 1 ) (t_1, y_1) (t1,y1) 开始且斜率为 f ( t 1 , y 1 ) f(t_1, y_1) f(t1,y1) 的线段上。继续进行,我们使用点 ( t k , y k ) (t_k, y_k) (tk,yk) 的斜率场来确定下一个点 ( t k + 1 , y k + 1 ) (t_{k+1}, y_{k+1}) (tk+1,yk+1)。
序列 y 0 , y 1 , y 2 , … y_0, y_1, y_2, \ldots y0,y1,y2,… 作为在时刻 t 0 , t 1 , t 2 , … t_0, t_1, t_2, \ldots t0,t1,t2,… 上解的近似值。从几何上讲,我们认为该方法是在连接 ( t k , y k ) (t_k, y_k) (tk,yk) 和 ( t k + 1 , y k + 1 ) (t_{k+1}, y_{k+1}) (tk+1,yk+1) 的一系列小线段(见图1.32)。基本上,我们将斜率场的小片段拼接在一起,形成一个近似我们的解曲线的图形。
该方法使用由斜率场给出的切线段来逼近解的图形。因此,在每个阶段,我们都会产生一个小误差(见图1.32)。希望如果步长足够小,这些误差在继续迭代时不会失控,且所得的图形接近于我们想要的解。
 图 1.31 斜率场中的步进过程
图 1.31 斜率场中的步进过程
 图1.32 精确解图像与Euler近似解的图像
图1.32 精确解图像与Euler近似解的图像
Euler 方法
为了将欧拉法付诸实践,我们需要一个公式由 ( t k , y k ) (t_k, y_k) (tk,yk) 确定 ( t k + 1 , y k + 1 ) (t_{k+1}, y_{k+1}) (tk+1,yk+1)。确定 t k + 1 t_{k+1} tk+1 很简单,我们在一开始就指定步长 Δ t \Delta t Δt,所以 t k + 1 = t k + Δ t
相关文章:

微分方程(Blanchard Differential Equations 4th)中文版Section1.4
1.4 NUMERICAL TECHNIQUE: EULER’S METHOD 上一节中讨论的斜率场的几何概念与近似微分方程解的基本数值方法密切相关。给定一个初值问题 d y d t = f ( t , y ) , y ( t 0 ) = y 0 , \frac{dy}{dt}=f(t,y), \quad y(t_0) = y_0, dtdy=f(t,y),y(t0)=y0, 我们可以通过首…...

求职Leetcode算法题(7)
1.搜索旋转排序数组 这道题要求时间复杂度为o(log n),那么第一时间想到的就是二分法,二分法有个前提条件是在有序数组下,我们发现在这个数组中存在两部分是有序的,所以我们只需要对前半部分和后半部分分别…...

ActiveMQ、RabbitMQ、Kafka、RocketMQ在事务性消息、性能、高可用和容错、定时消息、负载均衡、刷盘策略的区别
ActiveMQ、RabbitMQ、Kafka、RocketMQ这四种消息队列在事务性消息、性能、高可用和容错、定时消息、负载均衡、刷盘策略等方面各有其特点和差异。以下是对这些方面的详细比较: 1. 事务性消息 ActiveMQ:支持事务性消息。ActiveMQ可以基于JMS(…...

HanLP分词的使用与注意事项
1 概述 HanLP是一个自然语言处理工具包,它提供的主要功能如下: 分词转化为拼音繁转简、简转繁提取关键词提取短语提取词语自动摘要依存文法分析 下面将介绍其分词功能的使用。 2 依赖 下面是依赖的jar包。 <dependency><groupId>com.ha…...

Python 的进程、线程、协程的区别和联系是什么?
一、区别 1. 进程 • 定义:进程是操作系统分配资源的基本单位。 • 资源独立性:每个进程都有独立的内存空间,包括代码、数据和运行时的环境。 • 并发性:可以同时运行多个进程,操作系统通过时间片轮转等方式在不同…...

实时数据推送:Spring Boot 中两种 SSE 实战方案
在 Web 开发中,实时数据交互变得越来越普遍。无论是股票价格的波动、比赛比分的更新,还是聊天消息的传递,都需要服务器能够及时地将数据推送给客户端。传统的 HTTP 请求-响应模式在处理这类需求时显得力不从心,而服务器推送事件&a…...

数据守护者:SQL一致性检查的艺术与实践
标题:数据守护者:SQL一致性检查的艺术与实践 在数据驱动的商业世界中,数据的一致性是确保决策准确性和业务流程顺畅的关键。SQL作为数据查询和操作的基石,提供了多种工具来维护数据的一致性。本文将深入探讨如何使用SQL进行数据一…...

jenkins配置+vue打包多环境切换
jenkins配置流水线过程 1.新建item 加入相关的参数就行了。 流水线脚本设置 后端脚本 node {stage checkoutsh"""#每次打包清空工作空间目录rm -rf $workspace/*cd $workspace#到工作空间下从远端svn服务端拉取代码svn co svn://10.1.19.21/repo/技术中台/低…...

idea和jdk的安装教程
1.JDK的安装 下载 进入官网,找到你需要的JDK版本 Java Downloads | Oracle 中国 我这里是windows的jdk17,选择以下 安装 点击下一步,安装完成 配置环境变量 打开查看高级系统设置 在系统变量中添加两个配置 一个变量名是 JAVA_HOME …...

HTML静态网页成品作业(HTML+CSS)——电影网首页网页设计制作(1个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有1个页面。 二、作品演示 三、代…...

大数据系列之:Flink Doris Connector,实时同步数据到Doris数据库
大数据系列之:Flink Doris Connector,实时同步数据到Doris数据库 一、版本兼容性二、使用三、Flink SQL四、DataStream五、Lookup Join六、配置通用配置项接收器配置项查找Join配置项 七、Doris 和 Flink 列类型映射八、使用Flink CDC访问Doris的示例九、…...
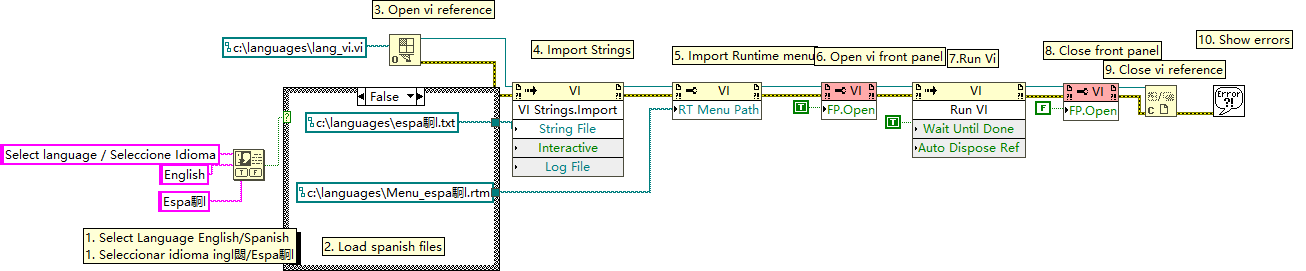
LabVIEW VI 多语言动态加载与运行的实现
在多语言应用程序开发中,确保用户界面能够根据用户的语言偏好动态切换是一个关键需求。本文通过分析一个LabVIEW程序框图,详细说明了如何使用LabVIEW中的属性节点和调用节点来实现VI(虚拟仪器)界面语言的动态加载与运行。此程序允…...

Unity引擎基础知识
目录 Unity基础知识概要 1. 创建工程 2. 工程目录介绍 3. Unity界面和五大面板 4. 游戏物体创建与操作 5. 场景和层管理 6. 组件系统 7. 脚本语言C# 8. 物理引擎和UI系统 学习资源推荐 Unity引擎中如何优化大型游戏项目的性能? Unity C#脚本语言的高级编…...

练习题- 探索正则表达式对象和对象匹配
正则表达式(Regular Expressions)是一种强大而灵活的文本处理工具,它允许我们通过模式匹配来处理字符串。这在数据清理、文本分析等领域有着广泛的应用。在Python中,正则表达式通过re模块提供支持,学习和掌握正则表达式对于处理复杂的文本数据至关重要。 本文将探索如何在…...

Java集合提升
1. 手写ArrayList 1.1. ArrayList底层原理细节 底层结构是一个长度可以动态增长的数组(顺序表)transient Object[] elementData; 特点:在内存中分配连续的空间,只存储数据,不存储地址信息。位置就隐含着地址。优点 节…...

uniapp 微信小程序生成水印图片
效果 源码 <template><view style"overflow: hidden;"><camera device-position"back" flash"auto" class"camera"><cover-view class"text-white padding water-mark"><cover-view class"…...

ElasticSearch相关知识点
ElasticSearch中的倒排索引是如何工作的? 倒排索引是ElasticSearch中用于全文检索的一种数据结构,与正排索引不同的是,正排索引将文档按照词汇顺序组织。而倒排索引是将词汇映射到包含该词汇的文档中。 在ElasticSearch中,倒排索…...

css 文字图片居中及网格布局
以下内容纯自已个人理解,直接上代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><…...

解决ImportError: DLL load failed while importing _rust: 找不到指定的程序
解决ImportError: DLL load failed while importing _rust: 找不到指定的程序 python使用库cryptography 当 from cryptography.hazmat.bindings._rust import exceptions as rust_exceptions 时,会报错: ImportError: DLL load failed while importin…...

集合-List去重
1.利用Set去重 @Test public void distinctList() {List<String> oldList = new ArrayList<>();oldList.add("a");oldList.add("a");oldList.add("b");oldList.add("c");oldList.add("d");List<String> …...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
