第十三届蓝桥杯省赛 python B组复盘
文章目录
- 前言
- 主要内容
- 🦞试题 A:排列字母
- 思路
- 代码
- 🦞试题 B:寻找整数
- 思路
- 代码
- 🦞试题 C:纸张尺寸
- 思路
- 代码
- 🦞试题 D:数位排序
- 思路
- 代码
- 🦞试题 E:蜂巢
- 思路
- 代码
- 🦞试题 F:消除游戏
- 思路
- 代码
- 🦞试题 G:全排列的价值
- 思路
- 代码
- 🦞试题 H:技能升级
- 思路
- 代码
- 🦞试题 I:最长不下降子序列
- 思路
- 代码
- 🦞试题 J:最优清零方案
- 思路
- 代码
- 总结
- 更多宝藏
前言
😎🥳😎
备战蓝桥杯第一弹–复盘

主要内容
🦞试题 A:排列字母

思路
(当时第一次参加蓝桥杯,当时现场心里小鹿乱撞,用排序输出了还每个字母数数验证一番(滑稽))
- 字符串转列表
- 列表排序
- 列表转字符串
代码
l = "WHERETHEREISAWILLTHEREISAWAY"
print(''.join(sorted(l)))
# AAAEEEEEEHHHIIILLRRRSSTTWWWY
🦞试题 B:寻找整数
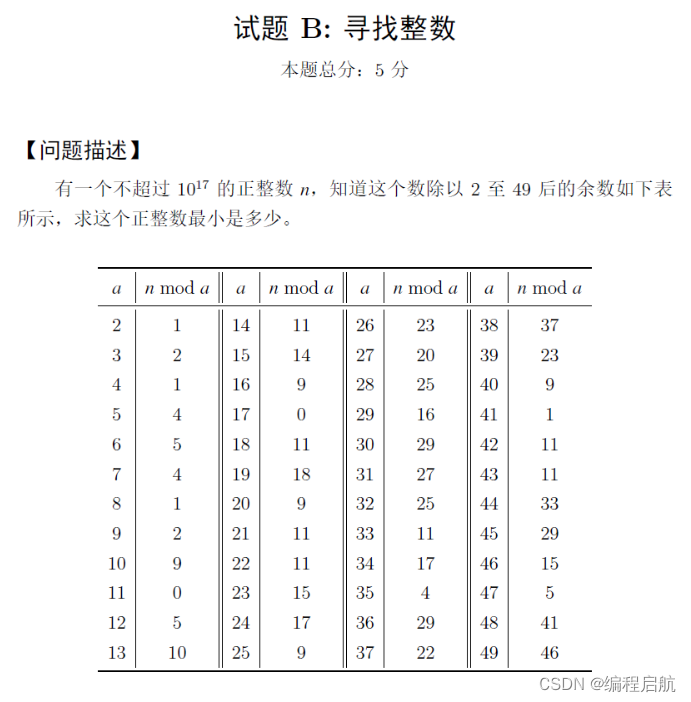
思路
当时在现场程序没跑出来
想着那个数取余2余1,取余4余1,取余8余1可以只看取余8余1的,因为满足后者一定满足前者,而满足前者不一定满足后者,不过当时没有想到找等差数列,一直在等最后的结果。。。
之后看大神的是有三个步骤:
暴力三步走:
1.枚举数据找规律:取表后面5个大数判断更容易找到大数据,得到关键数据。
2.找出规律求公式:这些数字是按判断求得的,所以一定存在公式。
3.遍历公式找答案:通过公式进行快速遍历,30s轻松找到十六位数的答案。
代码
#1.枚举数据找规律
i=1
while True:flag=Trueif i%49!=46:flag=Falseif i%48!=41:flag=Falseif i%47!=5:flag=Falseif i%46!=15:flag=Falseif i%45!=29:flag=Falseif flag:print(i)i+=1
'''
4772009
42909689
81047369
119185049
157322729
···
'''
#2.找出规律求公式
a=[4772009, 42909689, 81047369, 119185049,157322729]
#发现存在等差数列
print(a[1]-a[0])#38137680
print(a[2]-a[1])#38137680
print(a[3]-a[2])#38137680
k=38137680
b=4772009
#求出公式
y=k
#遍历公式
x=0
k=38137680
b=4772009
while True:flag=Truey=k*x+bfor i,j in mod:if y%i !=j:flag=Falsebreakif flag==True:print(y)#2022040920220409breakx+=1
🦞试题 C:纸张尺寸
题目描述
在 ISO 国际标准中定义了 A0 纸张的大小为 1189mm × 841mm,将 A0 纸沿长边对折后为 A1 纸,大小为 841mm × 594mm,在对折的过程中长度直接取下整(实际裁剪时可能有损耗)。将 A1 纸沿长边对折后为 A2 纸,依此类推。
输入纸张的名称,请输出纸张的大小。
输入
输入一行包含一个字符串表示纸张的名称,该名称一定是 A0、A1、A2、A3、A4、A5、A6、A7、A8、A9 之一。
输出
输出两行,每行包含一个整数,依次表示长边和短边的长度。
样例输入
A0
1
样例输出
1189
841
思路
当时就想着简单的判断循环
操作是折叠纸张
A几就是折叠几次,对应循环操作了几次
- 获取输入
- 循环次数
- 循环的操作
- 输出
代码
s = input() t = int(s[-1]) # 最后一个数字也就是迭代的次数
w,h = 1189,841for i in range(t):if w > h:w = w//2else:h = h//2
if w > h:print(w)print(h)
else:print(h)print(w)
🦞试题 D:数位排序
小蓝对一个数的数位之和很感兴趣,今天他要按照数位之和给数排序。当两个数各个数位之和不同时,将数位和较小的排在前面,当数位之和相等时,将数值小的排在前面。
例如,2022 排在 409 前面,因为 2022 的数位之和是 6,小于 409 的数位之和 13。
又如,6 排在 2022 前面,因为它们的数位之和相同,而 6 小于 2022。
给定正整数 n,m,请问对 1 到 n 采用这种方法排序时,排在第 m 个的元素是多少?
输入
输入第一行包含一个正整数 n。
第二行包含一个正整数 m。
输出
输出一行包含一个整数,表示答案。
样例输入
13
5
样例输出
3
提示
1 到 13 的排序为:1, 10, 2, 11, 3, 12, 4, 13, 5, 6, 7, 8, 9。第 5 个数为 3。
对于 30% 的评测用例,1 ≤ m ≤ n ≤ 300
对于 50% 的评测用例,1 ≤ m ≤ n ≤ 1000
对于所有评测用例,1 ≤ m ≤ n ≤ 106
思路
当时现场用的方法很绕写出来的,后来发现只是重新定义了一下排序规则
- 计算数位之和
- 定义排序规则
代码
n = int(input())
m = int(input())
l = [i for i in range(1,n+1)]
# 设置一个排序规则,计算数位之和
def fun(x):ans = 0while x:ans += x%10x = x//10return ans l.sort(key = fun)
print(l[m-1])
🦞试题 E:蜂巢
题目描述
蜂巢由大量的六边形拼接而成,定义蜂巢中的方向为:0 表示正西方向,1 表示西偏北 60◦,2 表示东偏北 60◦,3 表示正东,4 表示东偏南 60◦,5 表示西偏南 60◦。
对于给定的一点 O,我们以 O 为原点定义坐标系,如果一个点 A 由 O 点先向 d 方向走 p 步再向 (d + 2) mod 6 方向(d 的顺时针 120◦ 方向)走 q 步到达,则这个点的坐标定义为 (d, p, q)。在蜂窝中,一个点的坐标可能有多种。
下图给出了点 B(0, 5, 3) 和点 C(2, 3, 2) 的示意。
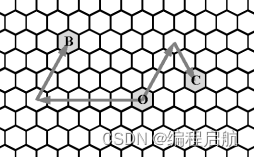
给定点 (d1, p1, q1) 和点 (d2, p2, q2),请问他们之间最少走多少步可以到达?
输入
输入一行包含 6 个整数 d1, p1, q1, d2, p2, q2 表示两个点的坐标,相邻两个整数之间使用一个空格分隔。
输出
输出一行包含一个整数表示两点之间最少走多少步可以到达。
样例输入
0 5 3 2 3 2
样例输出
7
提示
对于 25% 的评测用例,p1, p2 ≤ 103
对于 50% 的评测用例,p1, p2 ≤105
对于 75% 的评测用例,p1, p2 ≤107
对于所有评测用例,0 ≤ d1, d2 ≤ 5,0 ≤ q1 < p1 ≤ 109 ,0 ≤ q2 < p2 ≤ 109
思路
比赛的时候没有做出来,当时也是入门算法,读完题毫无思路,感慨万千
现在看了网上的回答用向量来做,将坐标的表达方式转化为向量,统一为0和1方向的向量。一共有六个方向,也就是六种计算方式。
代码
d1,p1,q1,d2,p2,q2=map(int,input().split())# 全部转化为0 方向 和 1方向的向量
def change(d,p,q):if d==0:return (p-q,q)if d==1:return (-q,p)if d==2:return (-p,p-q)if d==3:return (q-p,-q)if d==4:return (q,-p)if d==5:return (p,q-p)
s1=change(d1,p1,q1)
s2=change(d2,p2,q2)# 向量的减法
s=[s1[0]-s2[0],s1[1]-s2[1]]
a,b=s[0],s[1]
if a*b > 0: # ab同号print(abs(a+b))
else: # ab异号print(max(abs(a),abs(b)))
🦞试题 F:消除游戏
题目描述

输入
输入一行包含一个字符串 S 。
输出
输出一行包含一个字符串表示答案,如果结果为空则输出 EMPTY。
样例输入
edda
样例输出
EMPTY
样例输入
sdfhhhhcvhhxcxnnnnshh
样例输出
s
提示
对于 25% 的评测用例,|S | ≤ 103 ,其中 |S | 表示 S 的长度;
对于 50% 的评测用例,|S | ≤ 104
对于 75% 的评测用例,|S | ≤ 105
对于所有评测用例,|S | ≤ 106 ,S 中仅含小写字母。
思路
当时读完题感觉264非常大,直接写了一个无限循环,一直循环听说只可以过75%的数据
代码
s = input()
def f(x):s = set()for i in range(1,len(x)-1):if (x[i] == x[i-1] and x[i] != x[i+1]):s.add(i)s.add(i+1)elif (x[i] != x[i-1] and x[i] == x[i+1]):s.add(i-1)s.add(i) sr = ''for i in range(len(x)):if i not in s:sr += x[i]return sr
import copy
# 2的64次方操作
for i in range(1<<64):pre = copy.copy(s)s = f(s)if s == '':print('EMPTY')breakelif pre == s:print(s)break
🦞试题 G:全排列的价值

输入
输入一行包含一个整数 n 。
输出
输出一行包含一个整数表示答案,由于所有排列的价值之和可能很大,请输出这个数除以 998244353 的余数。
样例输入
3
样例输出
9
提示
1 至 3 构成的所有排列的价值如下:
(1, 2, 3) : 0 + 1 + 2 = 3
(1, 3, 2) : 0 + 1 + 1 = 2
(2, 1, 3) : 0 + 0 + 2 = 2
(2, 3, 1) : 0 + 1 + 0 = 1
(3, 1, 2) : 0 + 0 + 1 = 1
(3, 2, 1) : 0 + 0 + 0 = 0
故总和为 3 + 2 + 2 + 1 + 1 = 9
对于 40% 的评测用例,n ≤ 20
对于 70% 的评测用例,n ≤ 5000
对于所有评测用例,2 ≤ n ≤ 106
思路
当时在在考场上猜到是动态规划,一直在找规律,也不知道找对没
看大佬们的解法,太感人了,太优雅了
代码
MOD = 998244353
n = int(input().strip())
dp = 0
f = 1
for i in range(2,n+1):dp = (dp*i+f*i*(i-1)//2)%MODf = f*i%MOD
print(dp)
🦞试题 H:技能升级

样例输入
3 6
10 5
9 2
8 1
样例输出
47
提示
对于 40% 的评测用例,1 ≤ N, M ≤ 1000;
对于 60% 的评测用例,1 ≤ N ≤ 104 , 1 ≤ M ≤ 107;
对于所有评测用例,1 ≤ N ≤ 105,1 ≤ M ≤ 2 × 109,1 ≤ Ai , Bi ≤ 106。
思路
考场上用的是暴力,这里我们来看看大佬的思路
首先来说,我先自己做了一下,然后想到一个根据优先队列的做法,我只需要每次取得最优的,那我从某种意义来说,我们最后的结果就是最优的。
所以构建一个最大堆,然后每次取到最大的数,然后再push一个数进去,就是我们会更新我们的数,不过我们这个堆,一直都只有n个数据,我们把最大的pop出来以后,我们就可以进行更新,比如说减去b,或者变成0后不再进行技能升级。
所以依靠这样的想法,我就写了一下,而且我们在想,这样子,我们的读入数据是O(n),处理数据加上一个堆的排序,可能是nlogn,这样子应该是可以的。
这里提一下,我觉得最小堆和最大堆他是可以互换的,由于我好想发现heapq的最大堆没有push操作,那我就把数变成负的,这样我就利用最小堆构建了一个最大堆,因为加了一个负号后,最大的就变成最小的了
代码
import heapqn,m = map(int,input().split())
a,b = [],[]heap = []
for i in range(n):x,y = map(int,input().split())a.append(x)b.append(y)heapq.heappush(heap,(-x,i,0))cnt = 0
import math
for i in range(m):x,y,z = heapq.heappop(heap)if x == 0:breakx=-xcnt += x# x,y = nlargest(1,heap)if z > math.ceil(a[y]/b[y]): x = 0continueelse:x = x - b[y]heapq.heappush(heap,(-x,y,z+1))print(cnt)
🦞试题 I:最长不下降子序列

样例输入
5 1
1 4 2 8 5
样例输出
4
提示
对于 20% 的评测用例,1 ≤ K ≤ N ≤ 100;
对于 30% 的评测用例,1 ≤ K ≤ N ≤ 1000;
对于 50% 的评测用例,1 ≤ K ≤ N ≤ 10000;
对于所有评测用例,1 ≤ K ≤ N ≤ 105,1 ≤ Ai ≤ 106
思路
看看大佬怎末说
代码
🦞试题 J:最优清零方案
题目描述
给定一个长度为 N 的数列 A1, A2, · · · , AN。现在小蓝想通过若干次操作将这个数列中每个数字清零。
每次操作小蓝可以选择以下两种之一:
选择一个大于 0 的整数,将它减去 1;
选择连续 K 个大于 0 的整数,将它们各减去 1。
小蓝最少经过几次操作可以将整个数列清零?
输入
输入第一行包含两个整数 N 和 K。
第二行包含 N 个整数 A1, A2, · · · , AN。
输出
输出一个整数表示答案。
样例输入复制
4 2
1 2 3 4
样例输出复制
6
提示
对于 20% 的评测用例,1 ≤ K ≤ N ≤ 10。
对于 40% 的评测用例,1 ≤ K ≤ N ≤ 100。
对于 50% 的评测用例,1 ≤ K ≤ N ≤ 1000。
对于 60% 的评测用例,1 ≤ K ≤ N ≤ 10000。
对于 70% 的评测用例,1 ≤ K ≤ N ≤ 100000。
对于所有评测用例,1 ≤ K ≤ N ≤ 1000000, 0 ≤ Ai ≤ 1000000。
思路
代码
总结
🐋 🐬 🐶 🐳 🐰 🦀☝️ ⭐ 👉 👀
如果你对这篇文章感兴趣,欢迎在评论区留言,分享你的想法和建议。如果你喜欢我的博客,请记得点赞、收藏和关注我,我会持续更新更多有用的网页技巧和教程。谢谢大家!
更多宝藏
🍇🍉🍊🍏🍋🍅🥝🥥🫒🫕🥗
项目仓库看这里🤗:
https://github.com/w-x-x-w
https://gitee.com/w-_-x
博客文章看这里🤭:
https://blog.csdn.net/weixin_62650212
视频推送看这里🤤:
https://space.bilibili.com/1909782963
相关文章:

第十三届蓝桥杯省赛 python B组复盘
文章目录前言主要内容🦞试题 A:排列字母思路代码🦞试题 B:寻找整数思路代码🦞试题 C:纸张尺寸思路代码🦞试题 D:数位排序思路代码🦞试题 E:蜂巢思路代码&…...
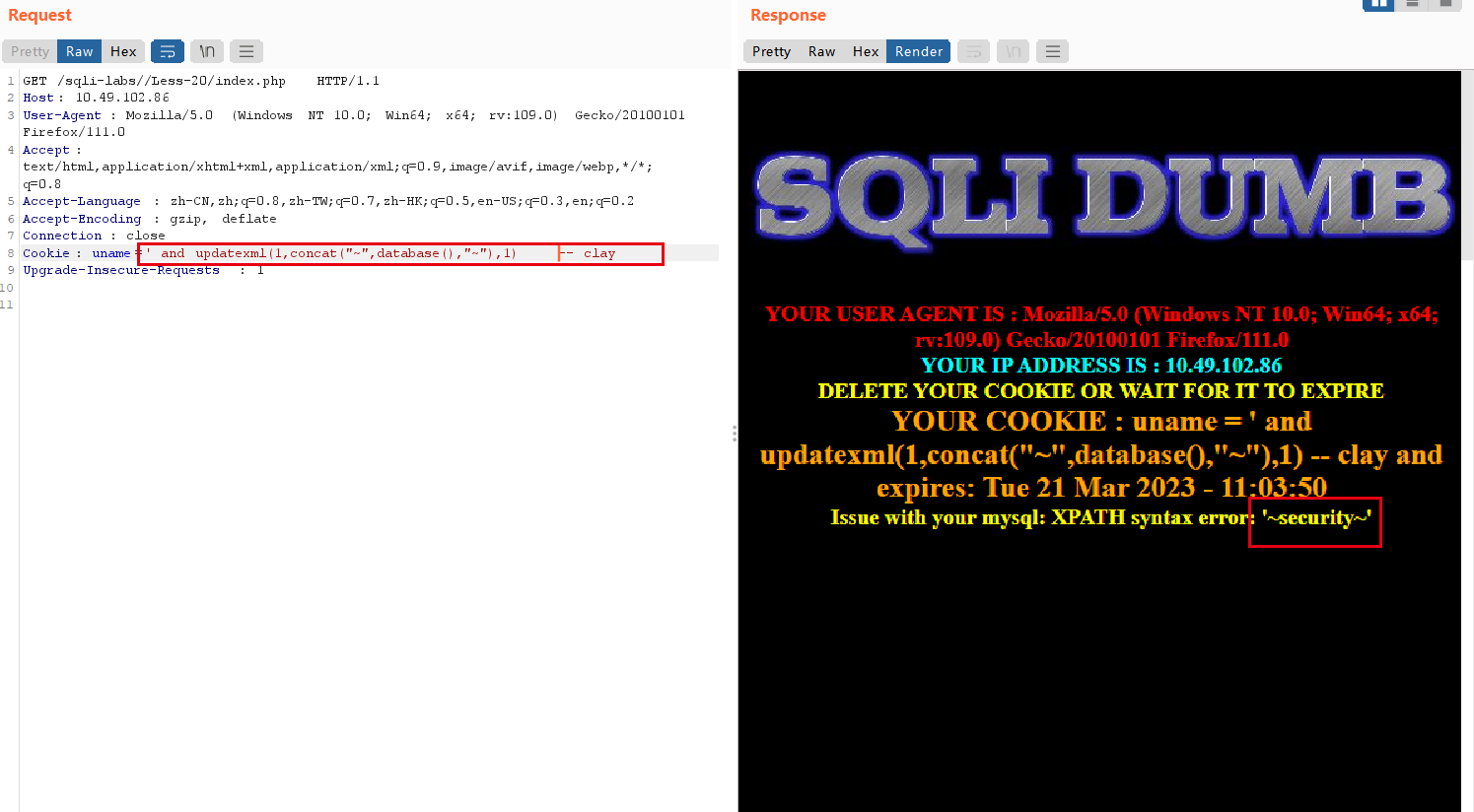
SQL注入之HTTP请求头注入
Ps: 先做实验,在有操作的基础上理解原理会更清晰更深入。 一、实验 sqli-lab 1. User-Agent注入 特点:登陆后返回用户的 User-Agent --> 服务器端可能记录用户User-Agent 输入不合法数据报错 payload: and updatexml(1,concat("~&…...

Metasploit详细教程
第一步:安装和启动Metasploit 您可以从Metasploit官方网站下载适用于您操作系统的Metasploit框架。安装Metasploit框架后,您可以使用以下命令来启动Metasploit: msfconsole该命令将启动Metasploit控制台。 第二步:查找目标设备…...

【ChatGPT】Notion AI 从注册到体验:如何免费使用
欢迎关注【youcans的GPT学习笔记】原创作品,火热更新中 【ChatGPT】Notion AI 从注册到体验1. Notion AI 介绍1.1 Notion AI 简介1.2 Notion AI 的核心能力1.3 Notion AI 与 ChatGPT 的比较2. Notion AI 国内用户注册2.1 PC 端用户注册2.2 移动端用户注册3. Notion …...
每个开发人员都需要掌握的10 个基本 SQL 命令
SQL 是一种非常常见但功能强大的工具,它可以帮助从任何数据库中提取、转换和加载数据。数据查询的本质在于SQL。随着公司和组织发现自己处理的数据量迅速增加,开发人员越来越需要有效地使用数据库来处理这些数据。所以想要暗恋数据领域,SQL是…...

Vue项目预渲染
前言 Ajax 技术的出现,让我们的 Web 应用能够在不刷新的状态下显示不同页面的内容,这就是单页应用。在一个单页应用中,往往只有一个 html 文件,然后根据访问的 url 来匹配对应的路由脚本,动态地渲染页面内容。单页应用…...

可别再用BeanUtils了(性能拉胯),试试这款转换神器
老铁们是不是经常为写一些实体转换的原始代码感到头疼,尤其是实体字段特别多的时候。有的人会说,我直接使用get/set方法。没错,get/set方法的确可以解决,而且也是性能较高的处理方法,但是大家有没有想过,要…...

Transformer 杂记
Transformer输入的是token,来自语言序列的启发。卷积神经网络(CNN)是如何进行物种分类的.它实际是直接对特征进行识别,也就是卷积神经网络最基本的作用:提取图像的特征。例如:卷积神经网络判断一只狗的时候,…...

实现异步的8种方式
前言异步执行对于开发者来说并不陌生,在实际的开发过程中,很多场景多会使用到异步,相比同步执行,异步可以大大缩短请求链路耗时时间,比如:「发送短信、邮件、异步更新等」,这些都是典型的可以通…...
Github隐藏功能显示自己的README,个人化你的Github主页
Github隐藏功能:显示自己的README 你可能还不知道,GitHub 悄悄上线了一个全新的个人页功能,显示一个自定义的 README.MD 在个人首页。要激活此功能,需要新建一个与自己 ID 同名的 Repository,新 Repo 里的README.MD将…...
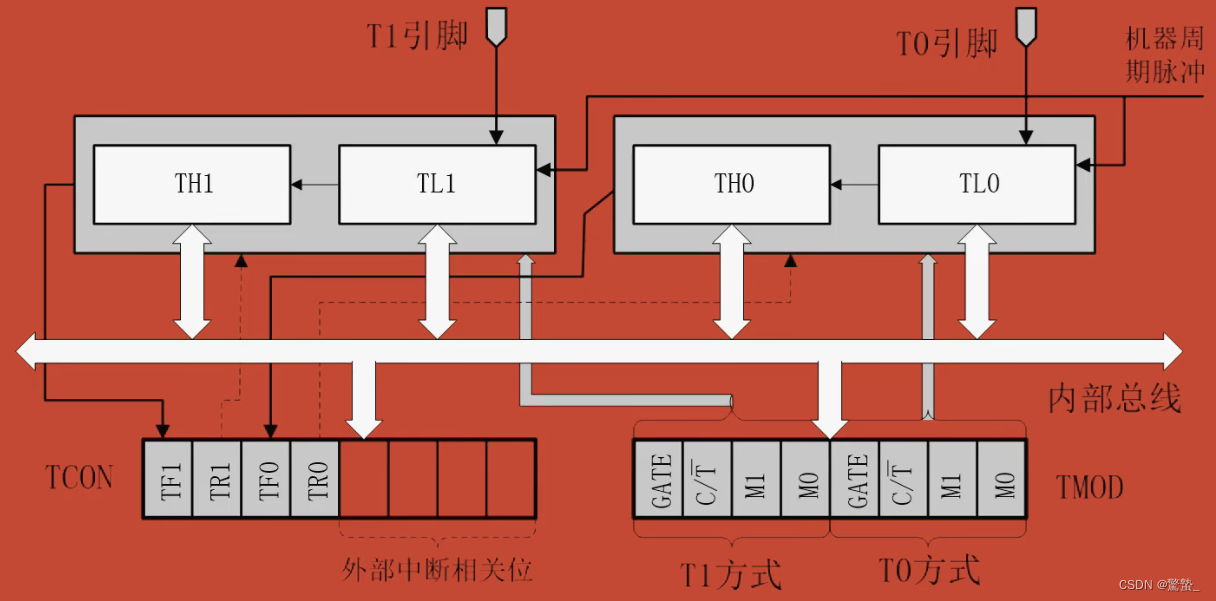
单片机 | 51单片机原理
【金善愚】 单片机应用原理篇 笔记整理 课程视频 :https://space.bilibili.com/483942191/channel/collectiondetail?sid51090 文章目录一、引脚分布介绍1.分类2.电源引脚3.时钟引脚(2根)4.控制引脚(4根)5.端口引脚(32根)二、存储器结构及空间分布介绍1.存储器的划…...
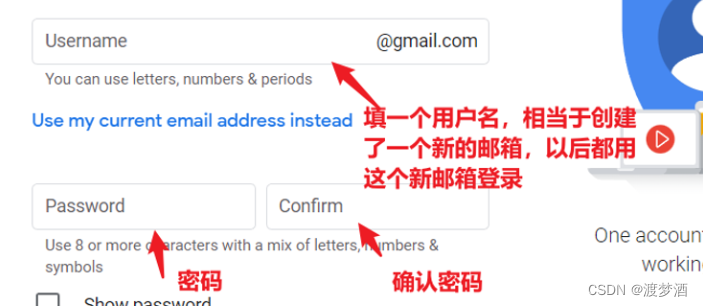
(只需五步)注册谷歌账号详细步骤,解决“此电话号码无法验证”问题
目录 第一步:打开google浏览器 第二步:设置语言为英语(美国) 第三步:点击重新启动,重启浏览器 第四步:开始注册 第五步,成功登录google账号! 如果出现这样的原因&…...
ChatGPT使用介绍、ChatGPT+编程、相关组件和插件记录
文章目录介绍认识ChatGPT是通过英汉互译来实现中文回答的吗同一个问题,为什么中英文回答不同ChatGPT的使用对话组OpenAI APIAI智能绘图DALLE 2ChatGPT for Google插件ChatGPT编程编写代码代码错误修正与功能解读代码评审与优化推荐技术方案编写和优化SQL语句在代码编…...

linux系统中复制粘贴和头文件问题解决方案
各位开发者大家好,好久不见,为了更好的服务大家,将平常所见所闻,以及遇到的问题和解决办法进行记录和总结。大家在学习过程中,有任何问题欢迎交流学习!!!。 第一:如何将w…...

Vue项目实战 —— 后台管理系统( pc端 ) —— Pro最终版本
前期回顾 开源项目 —— 原生JS实现斗地主游戏 ——代码极少、功能都有、直接粘贴即用_js斗地主_0.活在风浪里的博客-CSDN博客JS 实现 斗地主网页游戏https://blog.csdn.net/m0_57904695/article/details/128982118?spm1001.2014.3001.5501 通用版后台管理系统,如果…...

Springboot+vue开发的图书借阅管理系统项目源码下载-P0029
前言图书借阅管理系统项目是基于SpringBootVue技术开发而来,功能相对比较简单,分为两个角色即管理员和学生用户,核心业务功能就是图书的发布、借阅与归还,相比于一些复杂的系统,该项目具备简单易入手,便于二…...
学习 Python 之 Pygame 开发魂斗罗(十三)
学习 Python 之 Pygame 开发魂斗罗(十三)继续编写魂斗罗1. 创建敌人2类2. 编写敌人2类的draw()函数3. 编写敌人越界消失函数4. 编写敌人开火函数5. 把敌人2加入地图进行测试继续编写魂斗罗 在上次的博客学习 Python 之 Pygame 开发魂斗罗(十…...

指针进阶(中)
提示: 上集内容小复习🥰🥰 int my_strlen(const char* str) {return 1; } int main() {//指针数组char* arr[10];//数组指针int arr2[5] { 0 };int(*p)[5] &arr2; //p是一个指向数组的指针变量//函数指针int (*pf)(const char*)&m…...
,__BASE_FILE__))
C/C++获取文件名的方法(__FILE__,__builtin_FILE(),__BASE_FILE__)
目录标题C/C获取文件名的方法__FILE__宏避免__FILE__宏的错误慎用$(subst $(dir $<),,$<)\"")来重定义__BASE_FILE__宏__builtin_FILE()函数Windows API函数GetModuleFileName()getenv()使用cmake中的变量重定义__FILE__宏的CMake示例C/C获取文件名的方法 使用…...

线程池的讲解和实现
🚀🚀🚀🚀🚀🚀🚀大家好,今天为大家带来线程池相关知识的讲解,并且实现一个线程池 🌸🌸🌸🌸🌸🌸🌸🌸…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

