回溯算法——LeetCode37 解数独
题目
力扣题目链接
思路
- 卡哥的思路,注意看他解释为什么是“二维回溯”。
- 我的思路,类似y总解决 N 皇后问题时的第二种方法,即从左上到右下枚举棋盘的每个位置。
至于为什么与 N 皇后问题不一样,我认为是因为它每一行不止放一个,每一行的每个位置都要进行考虑。
代码
- 卡哥代码见上方思路。
- 我的代码:
class Solution {
private:bool isValid(int row, int col, char val, vector<vector<char>>& board) {// 判断该行是否有重复for (int i = 0; i < 9; i++) {if (board[row][i] == val) {return false;}}// 判断该列是否有重复for (int i = 0; i < 9; i++) {if (board[i][col] == val) {return false;}}// 判断九宫格内是否有重复// 很巧妙int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) {for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val) {return false;}}}return true;}// 有返回值是因为只需要找到一种可行的方案,好好理解一下bool backtracking(int x, int y, vector<vector<char>>& board) {// 遍历到一行的末尾了,就开始遍历下一行if (y == 9) {y = 0;x++;}// x == 9说明 0~8 这9行都遍历完了if (x == 9) {return true;}// 如果该位置还没填数的if (board[x][y] == '.') {// 遍历9种可能for (char i = '1'; i <= '9'; i++) {if (isValid(x, y, i, board)) {board[x][y] = i;if (backtracking(x, y + 1, board)) {return true;}board[x][y] = '.';}}// 9种都不行,就返回falsereturn false;}else {return backtracking(x, y + 1, board);}}public:void solveSudoku(vector<vector<char>>& board) {backtracking(0, 0, board);}
};
对于回溯函数为什么需要返回值的解释
ChatGPT:
你原来的代码(返回值为void)在找到一个解之后,会继续尝试其他可能的填充选项,并继续回溯,这样会导致找到的解可能会被覆盖,从而使最终输出的可能不是第一个找到的解,甚至可能无法正确地保留一个有效解。
详细分析
回溯的本质:
- 你的回溯算法会从左上角开始遍历整个数独网格。如果在某个位置找到了一个有效的填充数字,算法会继续前进,直到填满整个网格,或者无法找到合适的数字为止。
- 如果算法到达了一个无法继续的状态(即当前路径不再可行),它会回退到上一个状态并尝试其他可能的数字。
没有提前终止:
- 你的代码中没有检测到第一个有效解后提前终止的机制。
- 当回溯算法在最后一格填上数字时,虽然它找到了一个有效解,但是它不会立即返回,而是继续尝试回溯,试图寻找其他可能的解。
- 由于继续回溯,它可能会更改已经填好的数字,尝试其他路径,结果导致解被覆盖,或者递归无限循环而导致栈溢出(如你之前遇到的无限递归问题)。
覆盖问题:
- 在回溯过程中,每当你在一个位置填入一个数字后,都会立即调用递归函数进入下一步。
- 如果在某个位置找到的第一个有效数字满足所有条件,继续前进,最后递归完成一整次操作后,如果继续回溯,这个数字可能会被回溯掉,并试图用下一个数字替换。
- 因为没有及时终止,算法会尝试其他可能的数字组合,可能覆盖掉第一个找到的有效解。
解决方法
为了避免上述问题,关键在于:找到第一个有效解后立即终止进一步的回溯和搜索。这可以通过让递归函数在找到一个有效解时返回
true来实现,以阻止后续的任何修改。
相关文章:

回溯算法——LeetCode37 解数独
题目 力扣题目链接 思路 卡哥的思路,注意看他解释为什么是“二维回溯”。我的思路,类似y总解决 N 皇后问题时的第二种方法,即从左上到右下枚举棋盘的每个位置。 至于为什么与 N 皇后问题不一样,我认为是因为它每一行不止放一个…...

【CPP】继承语法详解与菱形继承
关于我: 睡觉待开机:个人主页 个人专栏: 《优选算法》《C语言》《CPP》 生活的理想,就是为了理想的生活! 作者留言 PDF版免费提供:倘若有需要,想拿我写的博客进行学习和交流,可以私信我将免费提供PDF版。…...

数据结构(6.2_1)——领接矩阵法
图的存储——邻接矩阵法 邻接矩阵(Adjacency Matrix)是一种使用二维数组来表示图的方法。在这种表示法中,矩阵的行和列都对应图的顶点。 特点 对于无向图,如果顶点i与顶点j之间有边,则矩阵的第i行第j列(…...

诈骗未成功是否构成犯罪?
诈骗未成功不一定构成犯罪。在刑法上,构成诈骗罪需要满足特定的构成要件,包括有非法占有的目的、实施了虚构事实或隐瞒真相的行为、对方因此陷入错误认识并处分财产、行为人或第三方取得财产、被害人遭受财产损失。如果诈骗行为未能成功,即被…...
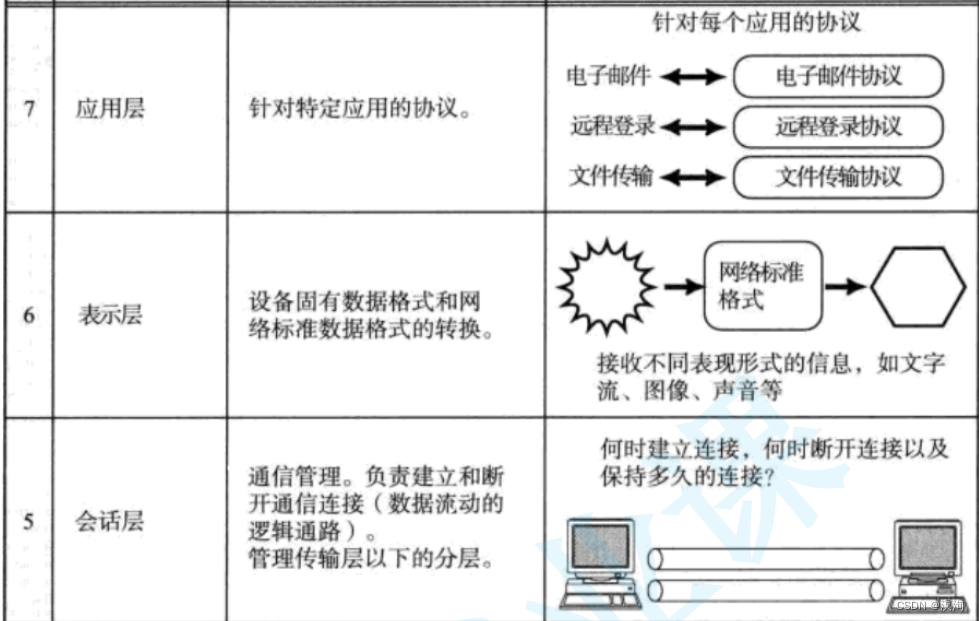
网络协议栈应用层的意义(内含思维导图和解析图通俗易懂超易理解)
绪论: “节省时间的方法就是全力以赴的将所要做的事情完美快速的做完,不留返工重新学习的时间,才能省下时间给其他你认为重要的东西。” 本章主要讲到OSI网络协议栈中的应用层的作用和再次在应用层的角度理解协议的具体意义,以及…...

【NXP-MCXA153】i2c驱动移植
介绍 I2C总线由飞利浦公司开发,是一种串行单工通信总线,它主要用于连接微控制器和其他外围设备并在总线上的器件之间传送信息(需要指定设备地址);常见的i2c设备有EEPROM、触摸屏、各种IoT传感器、时钟模块等&#x…...

C++(11)类语法分析(2)
C(10)之类语法分析(2) Author: Once Day Date: 2024年8月17日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可参考专栏: 源码分析_Once-Day的博客-CSDN博客 …...
)
数字验证每日十问--(3)
深拷贝和浅拷贝的区别? 当只拷贝对象中的成员变量和声明的句柄时,称为浅拷贝。浅拷贝只把对象中的句柄复制了,却没有复制句柄b所指向的对象。这会导致复制后,a2中的句柄b 和 a1 中的句柄b指向同一个对象,如果a2中的句…...

22.给定 n 对括号,实现一个算法生成所有可能的正确匹配的括号组合
22. Generate Parentheses 题目 给定 n 对括号,编写一个函数生成所有可能的正确匹配的括号组合。 例如,当 n = 3 时,可能的组合集合为: ["((()))","(()())","(())()","()(())","()()()" ]题目大意 给出 n 代表生成…...

检测到目标URL存在http host头攻击漏洞
漏洞描述 修复措施 方法一: nginx 的 default_server 指令可以定义默认的 server 去处理一些没有匹配到 server_name 的请求,如果没有显式定义,则会选取第一个定义的 server 作为 default_server。 server { …...

C++奇迹之旅:手写vector模拟实现与你探索vector 容器的核心机制与使用技巧
文章目录 📝基本框架🌠 构造和销毁🌉vector()🌉vector(const vector& v)🌉vector(size_t n, const T& value T())🌉赋值拷贝构造:vector<T>& operator(vector<T> v)&a…...

018、钩子函数 mounted和beforeDestroy、父组件向子组件传递参数 props 的使用
文章目录 1、mounted 和 beforeDestroy1.1、mounted1.2、beforeDestroy 2、父组件向子组件传递参数 props2.1、子组件定义2.2、父组件调用子组件并传参 3、完整例子3.1、父组件 Tags.vue3.2、子组件 TagsMenu.vue3.3、效果图 1、mounted 和 beforeDestroy 1.1、mounted mount…...

xlnt在Windows中的dll,lib生成
前言 花了半天时间想要把xlnt 集成到VS2022 Cmake项目中,以我目前掌握的能力,Cmake语法对于我来说难懂,对于只是使用过Cmake编译MySQL,或是其他lib,dll库的小白来说,不应该为了显示自己能力多么出众,强行去配置一些程序内容。 生活中没有绝对的事情,有舍有得. https://github…...

【网络】私有IP和公网IP的转换——NAT技术
目录 引言 NAT工作机制编辑 NAT技术的优缺点 优点 缺点 个人主页:东洛的克莱斯韦克-CSDN博客 引言 公网被子网掩码划分为层状结构,一个公网IP的机器又可以用很多私有IP搭建内网。在日常生活场景中用的都是私有IP,例如手机,…...

java 面试 PDF 资料整理
“尊贵的求知者,作者特此献上精心编纂的Java面试宝典PDF,这份资料凝聚了无数面试精华与实战经验,是通往Java技术殿堂的钥匙。若您渴望在Java编程的求职之路上稳健前行,只需轻轻一点,完成这象征支持与认可的一键三联&am…...

初步认识Linux系统
前言 Linux系统具有许多优点,不仅系统性能稳定,而且是开源软件。其核心防火墙组件性能高效、配置简单,保证了系统的安全。在很多企业网络中,为了追求速度和安全,Linux不仅仅是被网络运维人员当作服务器使用,…...

JavaScript AI 编程助手
JavaScript AI 编程助手 引言 随着人工智能技术的飞速发展,编程领域也迎来了前所未有的变革。JavaScript,作为全球最流行的编程语言之一,其与AI的结合为开发者带来了巨大的便利和无限的可能性。本文将探讨JavaScript AI编程助手的定义、功能…...

达梦数据库的系统视图v$datafile
达梦数据库的系统视图v$datafile 达梦数据库的V$DATAFILE 是一个重要的系统视图,提供了有关数据库数据文件的信息。 V$DATAFILE 系统视图 V$DATAFILE 视图用于显示数据库中每一个数据文件的详细信息。通过查询这个视图,数据库管理员可以了解数据文件的…...

Triton/window安装: triton-2.0.0-cp310-cp310-win_amd64.whl文件
下面这个github仓: https://github.com/PrashantSaikia/Triton-for-Windows/tree/main 安装命令也很简单,下载到本地后运行: pip install triton-2.0.0-cp310-cp310-win_amd64.whl...
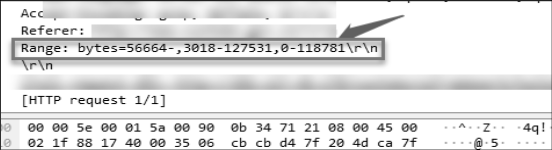
应急响应-DDOS-典型案例
某单位遭受DDoS攻击事件如下 事件背景 2019年2月17日,某机构门户网站无法访问,网络运维人员称疑似遭受DDoS攻击,请求应急响应工程师协助。 事件处置 应急响应工程师在达到现场后,通过查看流量设备,发现攻击者使用僵…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
