python 已知x+y=8 求x*y*(x-y)的最大值
先用导数求解
已知x+y=8
求xy(x-y)的最大值
令y=8-x
则 f(x)=x⋅(8−x)⋅(x−(8−x))=x⋅(8−x)⋅(2x−8)
导数方程为 f(x)'=-3x^2 + 24x - 32
求方程 − 3 x 2 + 24 x − 32 = 0 -3x^2 + 24x - 32 = 0 −3x2+24x−32=0 的根。
首先,我们可以尝试对方程进行因式分解。观察方程,我们可以发现它可以写成:
− 3 ( x 2 − 8 x + 32 3 ) = 0 -3(x^2 - 8x + \frac{32}{3}) = 0 −3(x2−8x+332)=0
但是,直接因式分解可能不太容易。因此,我们可以使用求根公式来找到方程的解。
对于一般形式的一元二次方程 a x 2 + b x + c = 0 ax^2 + bx + c = 0 ax2+bx+c=0,其解为:
x = − b ± b 2 − 4 a c 2 a x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} x=2a−b±b2−4ac
将我们的方程的系数代入求根公式,我们得到:
x = − 24 ± 2 4 2 − 4 × ( − 3 ) × ( − 32 ) 2 × ( − 3 ) x = \frac{-24 \pm \sqrt{24^2 - 4 \times (-3) \times (-32)}}{2 \times (-3)} x=2×(−3)−24±242−4×(−3)×(−32)
x = − 24 ± 576 − 384 − 6 x = \frac{-24 \pm \sqrt{576 - 384}}{-6} x=−6−24±576−384
x = − 24 ± 192 − 6 x = \frac{-24 \pm \sqrt{192}}{-6} x=−6−24±192
x = − 24 ± 8 3 − 6 x = \frac{-24 \pm 8\sqrt{3}}{-6} x=−6−24±83
这给出了两个解:
x 1 = − 24 + 8 3 − 6 = 4 − 4 3 3 x_1 = \frac{-24 + 8\sqrt{3}}{-6} = 4 - \frac{4\sqrt{3}}{3} x1=−6−24+83=4−343
x 2 = − 24 − 8 3 − 6 = 4 + 4 3 3 x_2 = \frac{-24 - 8\sqrt{3}}{-6} = 4 + \frac{4\sqrt{3}}{3} x2=−6−24−83=4+343
所以,方程 − 3 x 2 + 24 x − 32 = 0 -3x^2 + 24x - 32 = 0 −3x2+24x−32=0 的根是 x 1 = 4 − 4 3 3 x_1 = 4 - \frac{4\sqrt{3}}{3} x1=4−343 和 x 2 = 4 + 4 3 3 x_2 = 4 + \frac{4\sqrt{3}}{3} x2=4+343。
from scipy.optimize import minimize # 定义原函数
def func(x): return x * (8 - x) * (2 * x - 8) # 定义相反数函数
def neg_func(x): return -func(x) # 求相反数函数的极小值,即原函数的极大值
res = minimize(neg_func, x0=4) # x0是初始猜测值 # 输出结果
print("极大值点 x =", res.x)
print("极大值 y =", -res.fun) # 注意取相反数得到原函数的值

相关文章:

python 已知x+y=8 求x*y*(x-y)的最大值
先用导数求解 已知xy8 求xy(x-y)的最大值 令y8-x 则 f(x)x⋅(8−x)⋅(x−(8−x))x⋅(8−x)⋅(2x−8) 导数方程为 f(x)-3x^2 24x - 32 求方程 − 3 x 2 24 x − 32 0 -3x^2 24x - 32 0 −3x224x−320 的根。 首先,我们可以尝试对方程进行因式分解。观察…...

windows平台的postgresql主从数据库流备份
主: 操作系统:windows10 数据库版本:postgresql-16.2 ip:192.168.3.254 从: 操作系统:windows10 数据库版本:postgresql-16.2 ip:192.168.3.253 配置主库 配置 pg_hba.conf 文件 在 pg 的安装目录下,找到 …...

Spring 常见设计模式
什么是设计模式? 设计模式(Design pattern)是为解决软件设计中通用问题而被提出的一套指导性思想。它是一种被反复验证、经过实践证明并被广泛应用的代码设计经验和思想总结,可以帮助开发者通过一定的模式来快速的开发高质量、可维…...

优化大量数据导出到Excel的内存消耗(二):如果数据超出Excel单表上限,则进行分表
优化前:优化大量数据导出到Excel的内存消耗_大文件异步导出 内存占用高-CSDN博客 写Excel文件报错:Invalid row number (1048576) outside allowable range (0..1048575) 写入Excel时遇到IllegalArgumentException,原因是超出允许的最大行数…...

rustrover打开会报Error: Invalid toolchain
如果 cargo --version 正常输出,但在使用 RustRover 时出现“Invalid toolchain”错误,可能是由于 RustRover 工具链配置有问题或路径指向错误。 解决步骤: 1. 检查 RustRover 的工具链配置 打开 RustRover,进入 Preferences 或…...

docker-compose 安装canal
创建 Canal 配置文件 /conf/canal.properties mkdir -p conf/ touch /conf/canal.properties # canal.properties# tcp bind ip canal.ip 0.0.0.0 canal.port 11111 canal.metrics.pull.port 11112# zookeeper 集群配置 canal.zkServers canal.zookeeper.sessionTimeout…...

Unity动画模块 之 3D Rig页签
本文仅作笔记学习和分享,不用做任何商业用途本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 1.Rig页签 Rig 选项卡 - Unity 手册,rig是设置骨骼与替身系统的,工作流程如下 Avatar是什么…...

【蓝桥杯冲刺省一,省一看这些就够了-Java版本】蓝桥杯日期问题相关模板以及练习题
蓝桥杯历年省赛真题 点击链接免费加入题单 日期问题 java.time Java 中用于处理日期和时间的主要类位于 java.time 包中。以下是一些常用的类和其功能的简要介绍: LocalDate:表示日期。它提供了获取年、月、日以及日期之间比较的方法。 LocalDate to…...

【经典算法】BFS_FloodFill算法
目录 1, 算法介绍2,算法原理和代码实现(含题目链接)733.图像渲染200.岛屿的数量695.岛屿的最大面积130.被围绕的区域 3, 算法总结 1, 算法介绍 FloodFill(洪水灌溉) 算法介绍: 假设一个 4 * 4 的方格代表一块土地&am…...

RocketMQ之Topic主题详解
Topic概念定义 主题:RocketMQ中消息传输和存储的顶层容器,用于标识同类业务中逻辑的消息,可理解为消息的分类,主题消息的分类取决于业务,要发送的业务消息最好单独是一个Topic主题,以保证互相不被干扰Topi…...

实战OpenCV之图像显示
基础入门 OpenCV提供的功能非常多,图像显示是最基础也是最直观的一部分。它让我们能够直观地看到算法处理后的效果,对于调试和验证都至关重要。在OpenCV中,图像显示主要依赖于以下四个关键的数据结构和函数。 1、Mat类。这是OpenCV中最基本的…...

I2C的10-bit地址空间
10-bit地址空间: I2C支持 10-bit的设备地址,此时的时序如下图所示: 在 10-bit地址的 I2C系统中,需要两个帧来传输 slave的地址。第一个帧的前 5个 bit固定为 b11110,后接 slave地址的高 2位,第 8位仍然是 …...

TinyWebserver的复现与改进(6):定时器处理非活动连接
如果客户端长时间没有动作,会占用了许多连接资源,严重影响服务器的性能。因此需要通过实现一个服务器定时器,处理这种非活跃连接,释放连接资源。 定时器处理流程 SIGALARM触发:整个流程开始于一个 SIGALARM 信号&…...

ThinkPHP5 5.0.23 远程代码执行漏洞
目录 1、启动环境 2、漏洞利用 3、更改传参方式 4、修改参数 5、发送数据 1、启动环境 docker-compose up -d 2、访问靶机ip端口号8080 2、漏洞利用 使用burpsuite抓包软件抓包 3、更改传参方式 将 GET传参改为POST传参 4、修改参数 url参数 /index.php?scaptcha post参…...

C++鼠标键盘操作自动化
C鼠标键盘操作自动化 #pragma once #include <Windows.h> enum KEYS{A 65,W87,S83,D68,SHIFTVK_LSHIFT,ALT18,Tilde 126,//~TABVK_TAB,B66,SPACEVK_SPACE,ESCVK_ESCAPE,Q81 }; enum MOUSE {ML,MW,MR//左,中,右 }; class simulator//模拟器 { pu…...
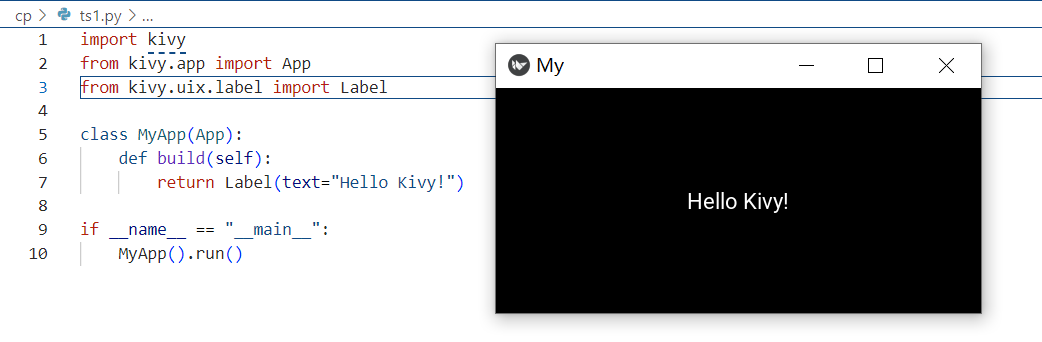
多个主流Python GUI库全面解析,助你用Python轻松构建精美界面
Python 作为一门易学易用的编程语言,在各个领域都拥有广泛的应用。而 GUI (Graphical User Interface) 编程更是让 Python 变得更加灵活,可以帮助我们创建各种各样的桌面应用,为用户提供直观的交互体验。本文将介绍几个Python GUI 编程中常用…...

Kotlin学习-01创建kotlin学习
安装idea https://www.jetbrains.com/zh-cn/ 创建项目 选择kotlin 修改Main.kt fun main() {print("Hello World!") }运行...

Java、python、php版的企业单位考勤打卡管理系统的设计与实现(源码、调试、LW、开题、PPT)
💕💕作者:计算机源码社 💕💕个人简介:本人 八年开发经验,擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等,大家有这一块的问题可以一起交流&…...

在IntelliJ IDEA中使用Git推送项目
去gitee网站注册用户 gitee网站地址:https://gitee.com/ github网站地址:https://github.com/ 一、创建仓库 以下以gitee为例进行介绍,github操作雷同。 1、创建仓库 点击页面右上方的"“并选择"创建仓库” 2、设置仓库相关信息 首先输入仓库名&…...

CNN代码实战
CNN的原理 从 DNN 到 CNN (1)卷积层与汇聚 ⚫ 深度神经网络 DNN 中,相邻层的所有神经元之间都有连接,这叫全连接;卷积神经网络 CNN 中,新增了卷积层(Convolution)与汇聚(…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
