P2460[SDOI2007] 科比的比赛
第一次做洛谷系列,紧张,请多关照哦
题目传送门:[SDOI2007] 科比的比赛 - 洛谷
思路分析
这道题大概题意是给定我们的主人公 Kobe Bryant 的 mm 个对手,nn 场比赛相对应的获胜概率。求 Kobe Bryant 最大全部获胜概率和打败对手能力值之和。
这道题可以使用 dfs 的思路解决。但是 Kobe Bryant 的对手非常多(也就是 mm 的值非常大),直接搜索的时间复杂度肯定非常高,就需要一些有效的剪枝。
最容易想到的是最优性剪枝,也就是如果当目前答案已经不优于已经存在的答案就可以直接放弃这个答案。
具体来说就是在 dfs 函数中加入:
if(cmp_double(tmp1,ans1)==0) return;
但是这样的优化显然是明显不够的。
这个题目有一个写的很明显特性是 n≤mn≤m。由于 nn 的值很小,而 Kobe Bryant 在每场比赛只能对战一个对手,所以 Kobe Bryant 只需要对战 nn 个对手并不是 mm 个。翻译成白话文就是 Kobe Bryant 可以只找弱的打,也就是找成功概率高的打。根据这个特性,我们可以在搜索时只搜前 nn 弱的对手。也可以理解这个剪枝是贪心的思路,因此 Kobe Bryant 的对手就少了很多。再根据前一条剪枝可以拿到 4040 分。
最后考虑到的是可以使用启发式搜索剪枝优化,对当前的结果进行估计,也就是即使是当前状态的最优情况,目前 Kobe Bryant 的获胜概率仍然没有已有最优情况高的时候舍弃。为了保证估计的效率,可以使用预处理的方式让每次询问复杂度降到 O(n)O(n)。
进行以上三次优化的思路是已经可以通过本题了。
代码
#include<bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define antirep(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
const int N=1e6,M=1e3;
const double err=1e-10;
bool vst[N];
double ans1,pr[N],Gl[N];
int n,m,a[N],ans2;
struct node{int id;double p;}k[M][M];
int cmp_double(double x,double y){if(abs(x-y)<err) return 2;if(x-y>err) return 1;if(x-y<err) return 0;return 0x7fffffff;
}
bool cmp(node x,node y){if(cmp_double(x.p,y.p)==2) return a[x.id]>a[y.id];return x.p>y.p;
}
int f(int cur,double tmp1){return cmp_double(tmp1*pr[cur],ans1);
}
void prepare(){pr[n]=k[n][1].p;antirep(i,n-1,1)pr[i]=pr[i+1]*k[i][1].p;
}
void dfs(int cur,double tmp1,int tmp2){if(cur>n){if(cmp_double(tmp1,ans1)==1||cmp_double(tmp1,ans1)==2){ans1=tmp1;if(tmp2>ans2) ans2=tmp2;}return;}if(cmp_double(tmp1,ans1)==0) return;if(f(cur,tmp1)==0)return;rep(i,1,n){int ID=k[cur][i].id;if(vst[ID]==1) continue;vst[ID]=1;tmp1*=k[cur][i].p,tmp2+=a[ID];dfs(cur+1,tmp1,tmp2);tmp1/=k[cur][i].p,tmp2-=a[ID],vst[ID]=0;}return;
}
signed main(){cin>>n>>m;rep(i,1,m) cin>>a[i];rep(i,1,n){rep(j,1,m)cin>>k[i][j].p,k[i][j].id=j;sort(k[i]+1,k[i]+1+m,cmp);}prepare();dfs(1,1,0);cout<<fixed<<setprecision(12)<<ans1<<endl;cout<<ans2<<endl;return 0;
}这里对代码进行一些解释,因为本题是浮点数操作,浮点数会在精度很高的时候产生误差,因此这里使用了 cmp_double 函数进行比较浮点数大小。
预处理之所以是逆序的储存是因为正序的搜索每次询问的都是剩余比赛的最有情况。
排序可以保证把 Kobe Bryant 最弱(也就是获胜概率最高)的对手放在每场比赛的最前面。
后记
备注:Kobe Bryant 是本题主人公科比的原名。而在 20202020 年,科比本人乘坐的西科斯基 S−76S−76 直升机在美国加利福尼亚州洛杉矶县卡拉巴萨斯市坠毁。年仅 4141 岁。
虽然我们不能跟题目重所描述的那样帮助科比赢得比赛,但是我们可以通过解出这道题淡化对科比离去的哀伤。
牢大,我想你了。
相关文章:

P2460[SDOI2007] 科比的比赛
第一次做洛谷系列,紧张,请多关照哦 题目传送门:[SDOI2007] 科比的比赛 - 洛谷 思路分析 这道题大概题意是给定我们的主人公 Kobe Bryant 的 mm 个对手,nn 场比赛相对应的获胜概率。求 Kobe Bryant 最大全部获胜概率和打败对手能…...

linux学习--第二天
--Linux文件系统 -显示文件命令 cat 1. cat -b 文件:从1开始对非空输出行编号 2. cat -n 文件:从1开始对所有行编号 3. cat -s 文件:将连续多行空白行合并 more(显示一屏文本内容) 1. more -num 文件ÿ…...

使用 Flask、Celery 和 Python 实现每月定时任务
为了创建一个使用 Flask、Celery 和 Python 实现的每月定时任务,我们需要按照以下步骤进行: 1.安装必要的库 我们需要安装 Flask、Celery 和 Redis(作为消息代理)。我们可以使用 pip 来安装它们: bash复制代码 p…...

【c语言】整数在内存中的储存(大小端字节序)
整数在内存中的储存(大小端字节序) 1.整数在内存中的储存 2.大小端字节序 3.整数在内存中储存例子 4.字节序判断 5.死循环现象 文章目录 整数在内存中的储存(大小端字节序)整数在内存中的储存大小端字节序什么是大小端为什么会有…...

浅谈SIMD、向量化处理及其在StarRocks中的应用
前言 单指令流多数据流(SIMD)及其衍生出来的向量化处理技术已经有了相当的历史,并且也是高性能数据库、计算引擎、多媒体库等组件的标配利器。笔者在两年多前曾经做过一次有关该主题的内部Geek分享,但可能是由于这个topic离实际研发场景比较远࿰…...

【ML】Image Augmentation)的作用、使用方法及其分类
图像增强(Image Augmentation)的作用、使用方法及其分类 1. 图像增强的定义2. 图像增强的作用3. 什么时候使用图像增强?4. 图像增强详细方法分类梳理4.1 图像增强方法列表4.2 边界框增强方法5. 参考资料 yolov3(一:模型…...
--单一职责原则)
设计模式六大原则(一)--单一职责原则
1. 简介 1.1. 概述 一个类或模块应该只负责完成一项任务或承担一个责任。如果一个类或模块承担了多个职责,那么当需要修改其中一个职责的功能时,就可能会对其他职责产生影响,从而导致代码耦合度增加,维护起来更加困难。 1.2. 主要特点 单一职责原则(Single Responsibi…...

c语言学习,malloc()函数分析
1:malloc() 函数说明: 申请配置size大小内存空间 2:函数原型: void *malloc(size_t size) 3:函数参数: 参数size,为申请内存大小 4:返回值: 配置成功则返回指针&#…...

【运维项目经历|041】上云项目-物理机迁移到阿里云
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专家博主 💊交流社区:CSDN云计算交流社区欢迎您的加入! 目录 项目名称 项目背景 项目目标 项…...
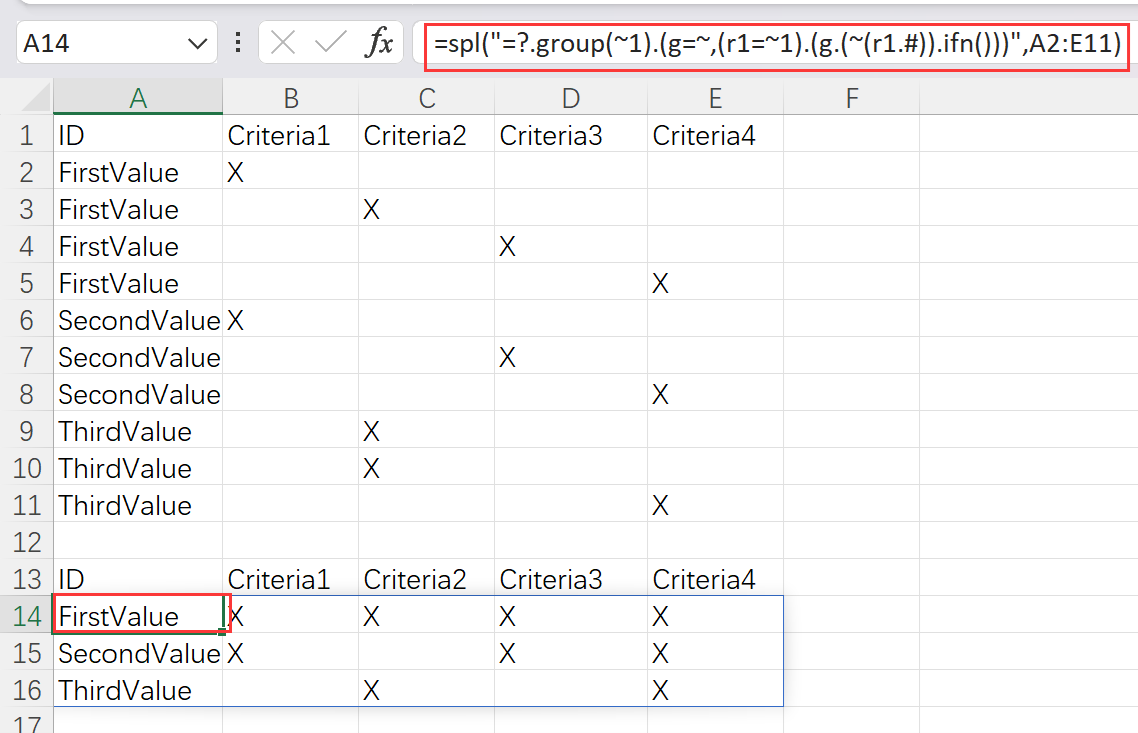
分组并合并其它列的非空值 --Excel难题#83
Excel第1列是分类,第2-42列是平行的多个数据项列,下表用部分列示例。数据有X或null两种情况,同一个分类的同一列数据偶尔有重复。 ABCDE1IDCriteria1Criteria2Criteria3Criteria42FirstValueX3FirstValueX4FirstValueX5FirstValueX6SecondVa…...

VM相关配置及docker
NAT——VMnet8网卡 桥接——WLAN/网线 仅主机——VMnet1网卡 docker与虚拟机的区别 启动docker服务 systemctl start docker 重启 systemctl start docker关闭docker服务 systemctl stop docker.servicedocker的两大概念 镜像:images,应用程序的静态文…...

Redis中Set数据类型常用命令
目录 1. 添加元素 2. 移除元素 3. 检查成员是否存在 4. 获取集合成员 5. 获取集合成员数量 6. 随机获取集合中的一个成员 7. 集合运算 8. 集合的移值 9. 提供集合的随机元素 在Redis中,Set是一种无序且不重复的字符串集合。 1. 添加元素 SADD key member [member ..…...

mysql误删数据恢复记录
背景 1、数据库版本 5.7.36,由于误操作删掉了表的所有数据,但是数据库备份每天凌晨进行、只能从备份恢复昨日的全量数据,当日的数据将会丢失 查看binlog配置 binlog配置 [mysqld] #设置日志三种格式:STATEMENT、ROW、MIXED 。 bi…...

论文阅读:Real-time Controllable Denoising for Image and Video
这篇文章是 CVPR 2023 的一篇文章,探讨了在图像与视频降噪中,如何实时控制降噪强度的问题。 Abstract 图像或者视频降噪,是在细节与平滑度之间的一个微妙的平衡,因为噪声与细节都属于高频信息,降噪在去除噪声的同时&…...

【Kubernetes】虚拟 IP 与 Service 的代理模式
虚拟 IP 与 Service 的代理模式 1.userspace 代理模式2.iptables 代理模式3.IPVS 代理模式 由于 Service 的默认发布类型是 ClusterlP,因此也可以把 ClusterIP 地址叫作 虚拟 IP 地址。在 Kubernetes 创建 Service 时,每个节点上运行的 kube-proxy 会自动…...

深度学习·Pytorch
以下代码源自李沐 自定义模块类 继承module类 继承nn.Module重写构造函数前向传播 class MLP(nn.Module):# 用模型参数声明层。这里,我们声明两个全连接的层def __init__(self):# 调用MLP的父类Module的构造函数来执行必要的初始化。# 这样,在类实例…...

fastzdp_sqlmodel新增get_first和is_exitsts方法
说明 经过fastzdp_login的整合,我们发现,fastzdp_sqlmodel还可以继续封装两个便捷的方法。 get_first:获取查询结果集中的第一条数据is_exitsts:判断数据是否已存在 封装get_first方法 def get_first(engine, model, query_di…...

嵌入式软件--数电基础 DAY 3
一、二进制 (1)文字表述 二进制数只能取0,1两个数字,逢二进一。 通过二进制表达文字。如战争时代的电报。 通过电灯泡的亮灭传递出信息。可以对灯亮和灯灭富裕一些含义,就能传达出想要的消息。 这就是编码和解码两…...

【生成式人工智能-十五-经典的影像生成方法-GAN】
经典的影像生成方法-GAN GANDiscriminatorGenerator还需要加入额外信息么 GAN可以加在其他模型上面我们可以用影像生成模型做什么? 前面讲过VAE和Flow-based以及diffusion Model ,今天讲最后一种经典的生成方法GAN。 GAN 前面讲的几种模型都是用加入额外…...

python 已知x+y=8 求x*y*(x-y)的最大值
先用导数求解 已知xy8 求xy(x-y)的最大值 令y8-x 则 f(x)x⋅(8−x)⋅(x−(8−x))x⋅(8−x)⋅(2x−8) 导数方程为 f(x)-3x^2 24x - 32 求方程 − 3 x 2 24 x − 32 0 -3x^2 24x - 32 0 −3x224x−320 的根。 首先,我们可以尝试对方程进行因式分解。观察…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
