人工智能与机器学习原理精解【12】
文章目录
- 分级聚类
- 理论
- 分级聚类的详细说明
- 1. 定义
- 2. 算法
- 3. 计算
- 4. 例子
- 5. 例题
- 皮尔逊相关系数
- julia实现
- 参考文献
分级聚类
理论
分级聚类的详细说明
1. 定义
分级聚类(Hierarchical Clustering),又称为层次聚类,是一种通过连续不断地将最为相似的群组两两合并,来构造出一个群组的层级结构的聚类方法。分级聚类是一种无监督学习算法,它不依赖于带有正确答案的样本数据进行训练,而是直接在一组数据中找寻某种结构。在分级聚类中,每个群组都是从单一元素开始的,通过不断合并,最终形成一个树状的层次结构。

2. 算法
分级聚类的基本算法过程如下:
- 初始化:每个数据点被视为一个单独的群组。
- 计算距离:计算每两个群组之间的距离或相似度。这通常基于数据点之间的距离度量,如欧氏距离、曼哈顿距离或皮尔逊相关系数等。
- 合并群组:选择距离最近(或相似度最高)的两个群组合并成一个新的群组。
- 重复迭代:重复上述步骤,直到所有的数据点都被合并成一个群组,或者达到某个预设的停止条件(如群组数量达到预设值)。
在分级聚类中,群组之间的距离有多种计算方式,包括但不限于:
- 最小距离法:群组之间的距离定义为两个群组中最近的两个数据点之间的距离。
- 最大距离法:群组之间的距离定义为两个群组中最远的两个数据点之间的距离。
- 平均距离法:群组之间的距离定义为两个群组中所有数据点对的平均距离。
- 重心法:群组之间的距离定义为两个群组的重心(或均值)之间的距离。
3. 计算
以皮尔逊相关系数为例,分级聚类的计算过程可能涉及以下步骤:
- 读取数据:从文件或数据库中读取待聚类的数据。
- 计算相关系数:使用皮尔逊相关系数公式计算每两个数据点之间的相似度。
- 构建距离矩阵:将相关系数转换为距离(或相似度)矩阵,其中每个元素表示两个数据点之间的距离(或相似度)。
- 合并群组:根据距离矩阵,选择距离最近(或相似度最高)的两个群组合并。
- 更新距离矩阵:合并后,需要重新计算新群组与其他群组之间的距离,并更新距离矩阵。
- 重复迭代:重复上述步骤,直到满足停止条件。
4. 例子
假设有以下五个数据点(以二维坐标表示):A(1,2)、B(2,3)、C(8,7)、D(6,5)、E(7,6)。使用分级聚类算法(以最小距离法为例)进行聚类,过程可能如下:
- 初始化:每个数据点被视为一个单独的群组。
- 计算距离:计算每两个数据点之间的距离,得到距离矩阵。
- 合并群组:选择距离最近的两个点(如A和B)合并成一个新的群组。
- 更新距离矩阵:计算新群组(AB)与其他数据点(C、D、E)之间的距离,并更新距离矩阵。
- 重复迭代:继续选择距离最近的两个群组合并,直到所有数据点都被合并成一个群组或达到预设的群组数量。
5. 例题
由于例题通常涉及具体的数学运算和详细的步骤,这里提供一个简化的示例问题:
问题:给定一组二维数据点,使用分级聚类算法(以最小距离法)进行聚类,并描述聚类过程。
解答:
- 读取数据:假设数据点已给出,如前面例子中的A、B、C、D、E。
- 计算距离:计算每两个数据点之间的距离,并确定哪两个点距离最近。
- 合并群组:将距离最近的两个点合并为一个新的群组,并更新群组列表。
- 重复迭代:继续计算新群组与其他群组之间的距离,并选择距离最近的两个群组合并,直到所有群组合并为一个或达到预设条件。
皮尔逊相关系数
皮尔逊相似度,在更严谨的学术表述中,通常被称为皮尔逊相关系数(Pearson Correlation Coefficient),是衡量两个变量之间线性相关程度的一个统计指标。
它的值域为[-1, 1],其中1表示完全正相关,-1表示完全负相关,0表示没有线性相关关系。
皮尔逊相关系数的计算公式为:
r = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}} r=∑i=1n(xi−xˉ)2∑i=1n(yi−yˉ)2∑i=1n(xi−xˉ)(yi−yˉ)
其中:
- n n n 是观测值的数量。
- x i x_i xi 和 y i y_i yi 分别是两个变量在第 i i i 个观测值上的取值。
- x ˉ \bar{x} xˉ 和 y ˉ \bar{y} yˉ 分别是 x x x 和 y y y 的平均值(即样本均值)。
计算步骤可以归纳为:
- 计算两个变量的平均值。
- 计算每个观测值与平均值的差。
- 计算这些差的乘积的和。
- 计算每个变量差的平方和,并开方得到标准差。
- 将步骤3的结果除以步骤4中两个标准差的乘积,得到皮尔逊相关系数。
julia实现
using Statistics
# 定义二叉树节点
struct TreeNode val :: Vector{Float64}left :: Union{TreeNode, Nothing} right :: Union{TreeNode, Nothing} function TreeNode(value, left=nothing, right=nothing) new(value, left, right) end
end function addLeftNode(a,b,parent_node)parent_node.left=TreeNode((a,b))
end
function addRightNode(a,b,parent_node)parent_node.right=TreeNode((a,b))
end#计算两个变量的平均值
function getMean(a,b) return mean.([a,b])
end#计算每个观测值与平均值的差
function getCha(a,b,mean_a,mean_b) return (a.-mean_a,b.-mean_b)
end#计算这些差的乘积的和
function getChaSum(cha_a,cha_b)return sum(cha_a.*cha_b)
end# 计算每个变量差的平方和,并开方得到标准差
function getChaSumSqrt(cha_a,cha_b)return (sqrt(sum(cha_a.^2)),sqrt(sum(cha_b.^2)))
end#得到皮尔逊相关系数
function getR(a,b)mean_a,mean_b=getMean(a,b)cha_a,cha_b=getCha(a,b,mean_a,mean_b)cha_sum=getChaSum(cha_a,cha_b)Cha_a_sumsqrt,Cha_b_sumsqrt=getChaSumSqrt(cha_a,cha_b)return cha_sum/(Cha_a_sumsqrt*Cha_b_sumsqrt)
end lst::Vector{Vector{Float64}}=[[20.,15.,124.],[73.,26.,71.],[99.,69.,132.],[33.,111.,128.],[241.,8.,71.],[19.,109.,41.]]
node_lst::Vector{TreeNode}=TreeNode.(lst)function getBestR(lst::Vector{Vector{Float64}}) ab_r_lst=[(i,j,1.0-abs(getR(lst[i],lst[j]))) for i in 1:length(lst) for j in 1:length(lst) if i != j]ab_r_matrix=fill(1.5,length(lst),length(lst))for d_r in ab_r_lsti,j,r=d_rab_r_matrix[i,j]=rendmin_r_val, id_r = findmin(ab_r_matrix) min_a_id= id_r[1]min_b_id=id_r[2]return (min_a_id,min_b_id)
endfunction groupNode(lst::Vector{Vector{Float64}},node_lst::Vector{TreeNode})if length(lst)==1return node_lst[1]endmin_a_id,min_b_id=getBestR(lst)right_node=node_lst[min_b_id]left_node=node_lst[min_a_id]root_node_value=((left_node.val).+right_node.val)/2.0root_node=TreeNode(root_node_value,left_node,right_node) deleteat!(lst,sort([min_a_id,min_b_id]))deleteat!(node_lst,sort([min_a_id,min_b_id]))push!(lst,root_node_value)push!(node_lst,root_node)groupNode(lst,node_lst)
endfunction levelOrder(root::TreeNode) if isnothing(root) return [] end # 使用 Vector 模拟队列 queue = [root] result = [] while !isempty(queue) # 当前层的节点数 level_size = length(queue) # 当前层的值列表 level_values = [] for _ in 1:level_size # 弹出队列的前端节点 node::TreeNode = popfirst!(queue) # 注意:popfirst! 会移除并返回数组的第一个元素 push!(level_values, node.val) # 如果左子节点存在,加入队列 if !isnothing(node.left) push!(queue, node.left) end # 如果右子节点存在,加入队列 if !isnothing(node.right) push!(queue, node.right) end end # 将当前层的值列表添加到结果中 push!(result, level_values) end return result
endroot=groupNode(lst,node_lst)
result = levelOrder(root)
println(result)Any[Any[[56.8125, 43.34375, 118.9375]], Any[[93.625, 71.6875, 113.875], [20.0, 15.0, 124.0]], Any[[88.25, 74.375, 95.75], [99.0, 69.0, 132.0]], Any[[143.5, 37.75, 63.5], [33.0, 111.0, 128.0]], Any[[46.0, 67.5, 56.0], [241.0, 8.0, 71.0]], Any[[19.0, 109.0, 41.0], [73.0, 26.0, 71.0]]]* Terminal will be reused by tasks, press any key to close it.
参考文献
1.文心一言
相关文章:

人工智能与机器学习原理精解【12】
文章目录 分级聚类理论分级聚类的详细说明1. 定义2. 算法3. 计算4. 例子5. 例题 皮尔逊相关系数 julia实现 参考文献 分级聚类 理论 分级聚类的详细说明 1. 定义 分级聚类(Hierarchical Clustering),又称为层次聚类,是一种通过…...

openEuler系统安装Visual Studio Code
openEuler系统安装Visual Studio Code 背景安装密钥和存储库更新包缓存并使用dnf安装包Fedora 22及以上版本旧版本使用yum 安装过程截图安装成功看桌面效果 背景 openEuler(openEuler-24.03-LTS)安装了麒麟UKUI桌面但是没有麒麟软件商店想安装Visual Studio Code 安装密钥和…...

Qt 系统相关 - 事件
目录 1. 事件介绍 2. 事件的处理 示例1:处理鼠标进入和离开 示例2:当鼠标点击时,获取对应的坐标值; 3. 按键事件 3.1 单个按键 3.2 组合按键 4. 鼠标事件 4.1 鼠标单击事件 4.2 鼠标释放事件 4.3 鼠标双击事件 4.4 鼠标…...

Ubuntu最小化命令行系统 安装GUI 远程桌面
Ubuntu 服务器 安装GUI 更新、升级 sudo apt update && sudo apt upgrade安装桌面环境 sudo apt install taskselsudo apt install ubuntu-desktop安装显示登录管理器 sudo apt install lightdm安装 lightdm 时系统会让选择默认的显示管理器,选择lightd…...
背景,文本,链接)
Web前端:CSS篇(二)背景,文本,链接
CSS 背景 背景颜色 background-color 属性定义了元素的背景颜色. 页面的背景颜色使用在body的选择器中: body {background-color:#b0c4de;} CSS中,颜色值通常以以下方式定义: 十六进制 - 如:"#ff0000"RGB - 如:"rgb(255,0…...

ubuntu 24.04 软件源配置,替换为国内源
ubuntu 默认的官网源下载速度非常慢,新装 ubuntu 系统首先把 apt 软件源替换成国内源。 1、使用软件和更新设置国内源 打开软件和更新,选择位于中国的服务器: 外链图片转存失败,源站可能有防盗链机制,建议将图片保存…...

【Java 并发编程】(三) 从CPU缓存开始聊 volatile 底层原理
并发编程 三大问题 在并发编程中,原子性、有序性和可见性是三个重要的问题,解决这三个问题是保证多线程程序正确性的基础。原子性: 指的是一个操作不可分割, 要么全部执行完成, 要么不执行, 不存在执行一部分的情况.有序性: 有序性是指程序的执行顺序与…...

YOLOV8网络结构|搞懂Backbone-Conv
参数量计算: (输入通道*w)*(输出通道*w)*k^2+(输出通道*w)*2 w是模型缩放里面的width - [-1, 1, Conv, [64, 3, 2]] # 0-P1/2 输出通道c2=64,k=3,s=2 P1/2 特征图变小一半 先定义算子层 再搭一个forward前向传播 class Conv(nn.Module):"""Standard convo…...

Elasticsearch Nested类型详解与实战
Elasticsearch(简称ES)是一个基于Lucene的全文搜索引擎,它提供了强大的搜索能力以及对数据的高效索引和查询。在ES中,数据通常以JSON格式存储,并且可以采用多种数据类型。其中,nested类型是一种特殊的对象数…...
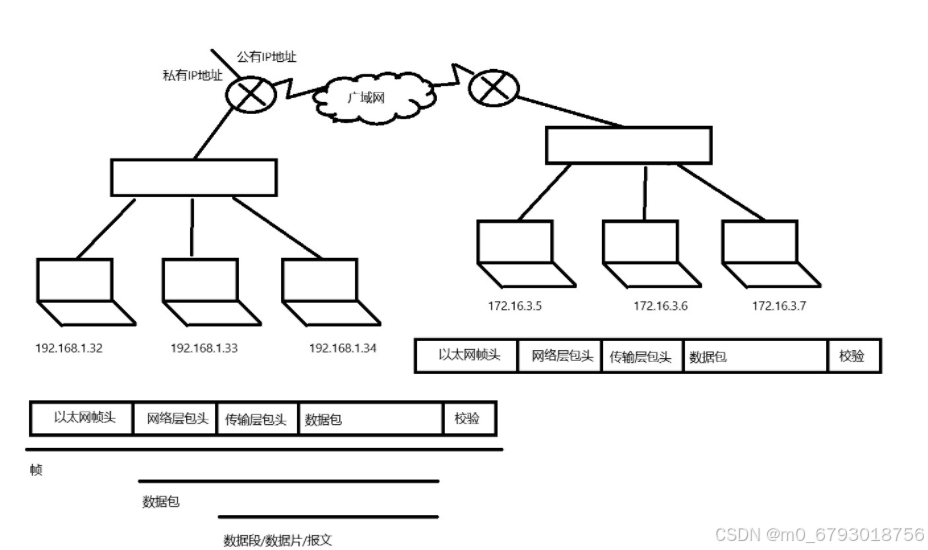
网络编程,网络协议,UDP协议
网络: 1.协议:通信双方约定的一套标准 2.国际网络通信协议标准: 1.OSI协议: 应用层 发送的数据内容 表示层 数据是否加密 会话层 是否建立会话连接 传输层 …...

每日一题——第六十三题
题目:判断一个数是否为合数 #include <stdio.h> #include <stdbool.h> // 为了使用bool类型 // 函数声明,用于判断是否为合数 bool isComposite(int x); int main() { int x; printf("请输入一个正整数: "); scanf(&quo…...

人工智能算法,图像识别技术;基于大语言模型的跨境商品识别与问答系统;图像识别
目录 一 .研究背景 二,大语言模型介绍 三,数据采集与预处理 商品识别算法 四. 跨境商品问答系统设计 五.需要源码联系 一 .研究背景 在当今全球化的背景下,跨境电商行业迅速发展,为消费者提供了更广泛的购物选择和更便利的购物方式。然而…...

数据库系统 第18节 数据库安全
数据库安全是确保数据库管理系统(DBMS)中存储的数据的保密性、完整性和可用性的过程。以下是一些关键的数据库安全措施: 用户身份验证(Authentication): 这是确定用户或系统是否有权访问数据库的第一步。通…...

Golang | Leetcode Golang题解之第338题比特位计数
题目: 题解: func countBits(n int) []int {bits : make([]int, n1)for i : 1; i < n; i {bits[i] bits[i&(i-1)] 1}return bits }...

【Python变量简析】
Python变量简析 在 Python 中,变量是用于存储和操作数据的命名内存位置。变量的概念类似于代数中的方程变量,比如对于方程式 y x * x ,x 就是变量。 Python 变量具有以下特点: 变量名可以由字母、数字和下划线组成,…...

智慧零售模式下物流优化与开源AI智能名片S2B2C商城系统的深度融合
摘要:在数字化浪潮的推动下,智慧零售模式正逐步成为零售业的新常态。该模式通过深度融合物联网、大数据、人工智能等先进技术,实现了线上线下无缝衔接,为消费者提供了更加便捷、个性化的购物体验。物流作为智慧零售的重要支撑&…...

socket和websocket 有什么区别
Socket 和 WebSocket 都用于网络通信,但它们的用途、协议、以及使用方式有所不同。以下是两者的主要区别: ### 1. **基础协议** - **Socket**: - Socket 是网络通信的一个抽象概念,通常基于传输层协议,如 TCP(…...
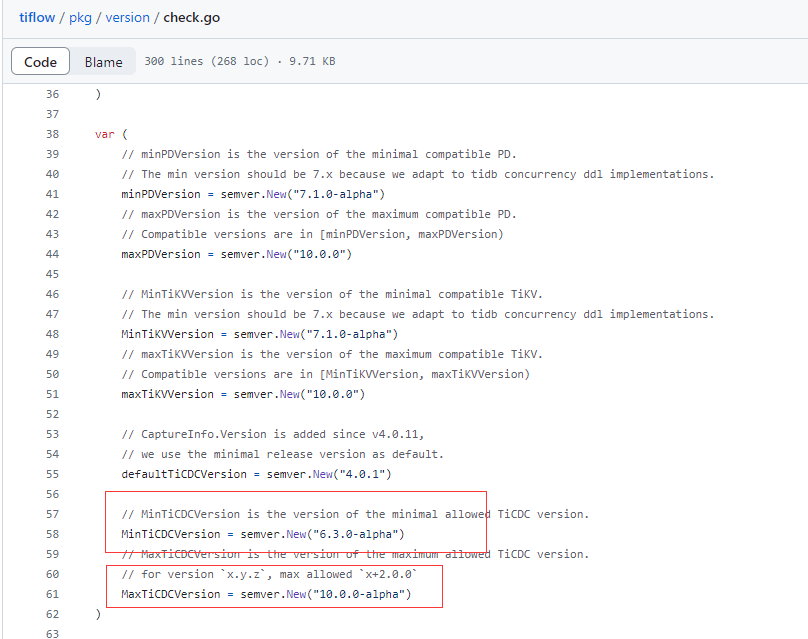
亿玛科技:TiDB 6.1.5 升级到 7.5.1 经验分享
作者: foxchan 原文来源: https://tidb.net/blog/6e628afd 为什么要升级? 本次升级7.5的目的如下: 1、tidb有太多的分区表需要归档整理。7.5版本这个功能GA了。 2、之前集群tikv节点的region迁移过慢,影响tikv节…...

8.16-ansible的应用
ansible ansible是基于模块工作的,本身没有批量部署的能力。真正具有批量部署的是ansible所运行的模块,ansible只是提供一种框架。 格式 ansible 主机ip|域名|组名|别名 -m ping|copy|... 参数 1.ping模块 m0 # 查看有没有安装epel [rootm0 ~]#…...
相似度计算方法-编辑距离 (Edit Distance)
定义 编辑距离(Edit Distance),也称为Levenshtein距离,是一种衡量两个字符串相似度的方法。它定义为从一个字符串转换为另一个字符串所需的最少单字符编辑操作次数,这些操作包括插入、删除或替换一个字符。 计算方法 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
