C++:平衡二叉搜索树之红黑树
一、红黑树的概念
红黑树, 和AVL都是二叉搜索树, 红黑树通过在每个节点上增加一个储存位表示节点的颜色, 可以是RED或者BLACK, 通过任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树能够确保没有一条路径会比其他路径长出两倍,因此红黑树是接近平衡的。
与AVL树相比,红黑树的插入和删除操作更具优势,因为红黑树是接近平衡的,AVL树是绝对平衡的, 因此插入删除等操作时,红黑树需要旋转的次数是比AVL树少的。
二、红黑树的性质
- 每个节点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子节点是黑色的
- 一条路径上没有连续的红色节点, 每条路径上黑色节点的数量是相同的
下面就是一个红黑树的示例:
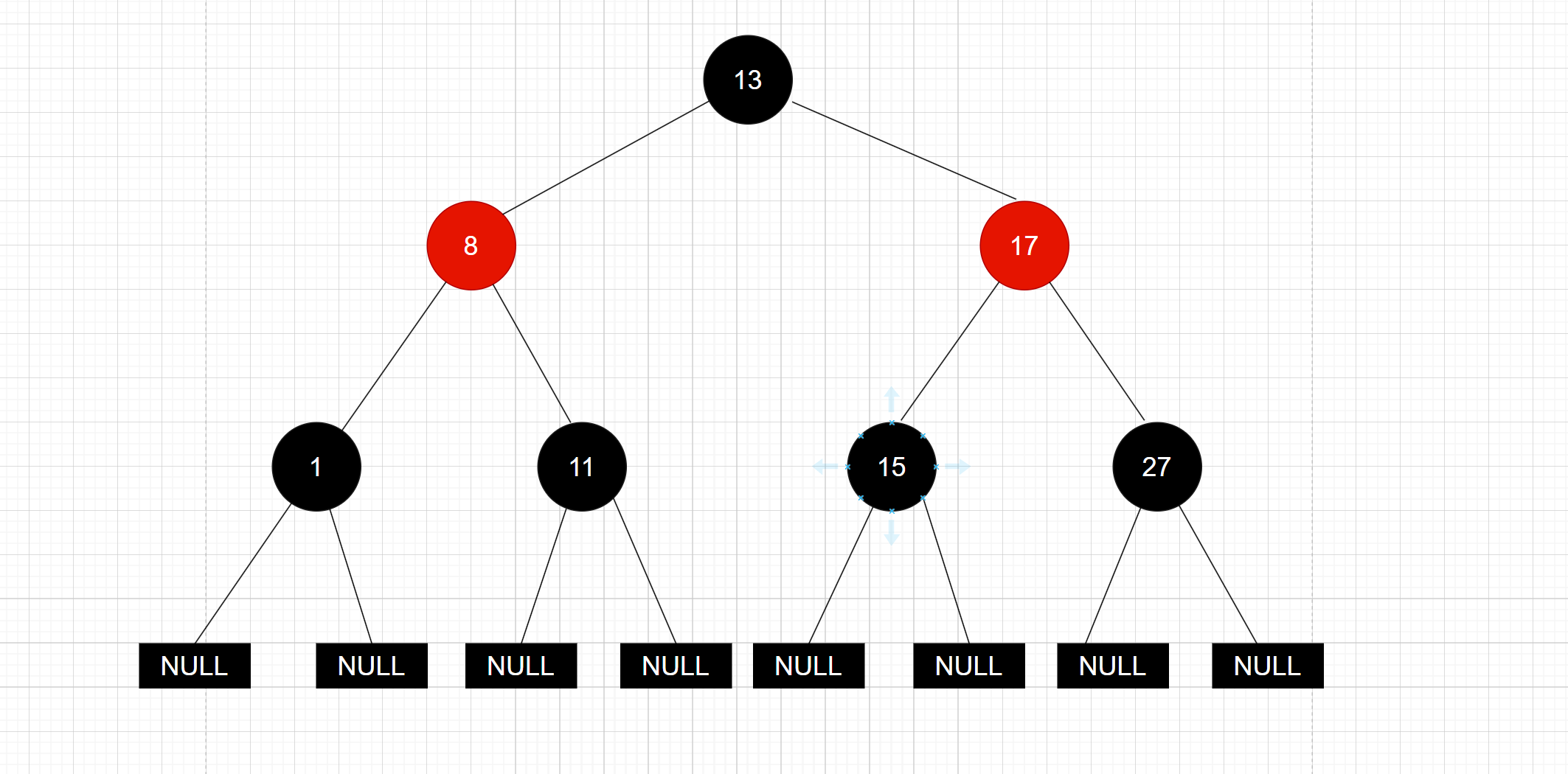
根据红黑树的性质我们知道:一个红黑树中,最短路径 * 2 >= 最长路径
理论上:最短路径:全黑 最长路径:一黑一红交替
三、红黑树节点的定义
下面是红黑树节点的定义代码:
//节点的颜色定义
enum Colour
{RED,BLACK
};
//节点结构体
template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;//节点的数据RBTreeNode<K, V>* _left;//节点的左孩子RBTreeNode<K, V>* _right;//节点的右孩子RBTreeNode<K, V>* _parent;//节点的双亲节点Colour _col;//节点的颜色//节点的构造函数RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}
};
四、红黑树的插入
红黑树是在二叉搜索树的基础上加上使其近似平衡的限制条件, 因此红黑树的插入可以分成以下两步:
1、按照二叉搜索树的性质插入新节点
2、检测新节点插入后,红黑树的性质是否遭到破坏
新节点的默认颜色是红色,因此,如果双亲节点是黑色就没有违反任何红黑树的性质,不需要调整,但是如果新插入节点的双亲节点是红色时, 就违反了不能有相连的红色节点的规则,此时需要对红黑树进行分情况讨论:
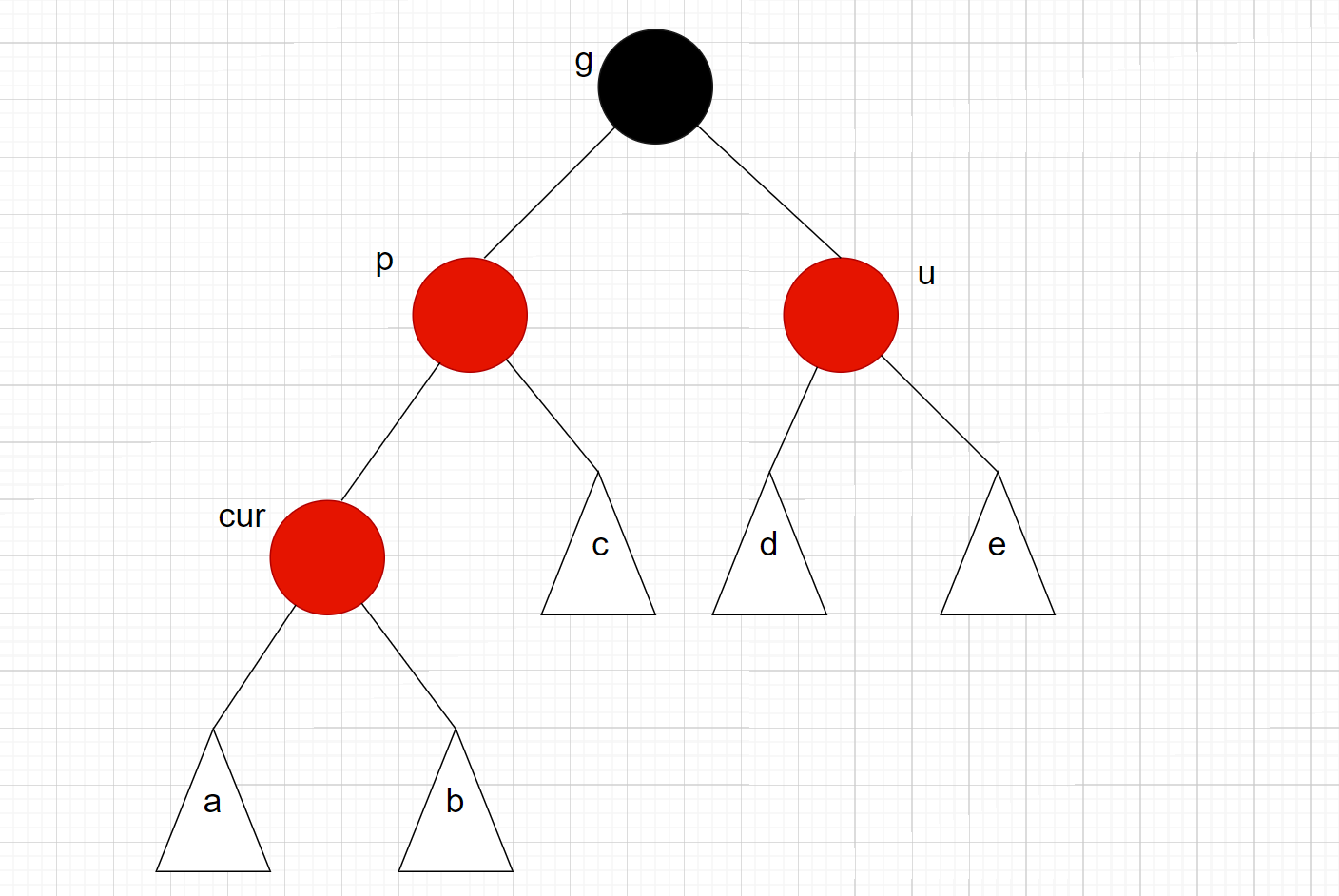
cur为当前节点, p为父节点, g为祖父节点, u为叔父节点
4.1情况一:cur 为红, p为红, g为黑, u存在且为黑
注意:这里的树,可能是一棵完整的树, 也可能是一个子树
此时abcde子树都为空
这个时候我们只需要进行变色处理, 将p 和 u节点变为黑色, 将g改为红色
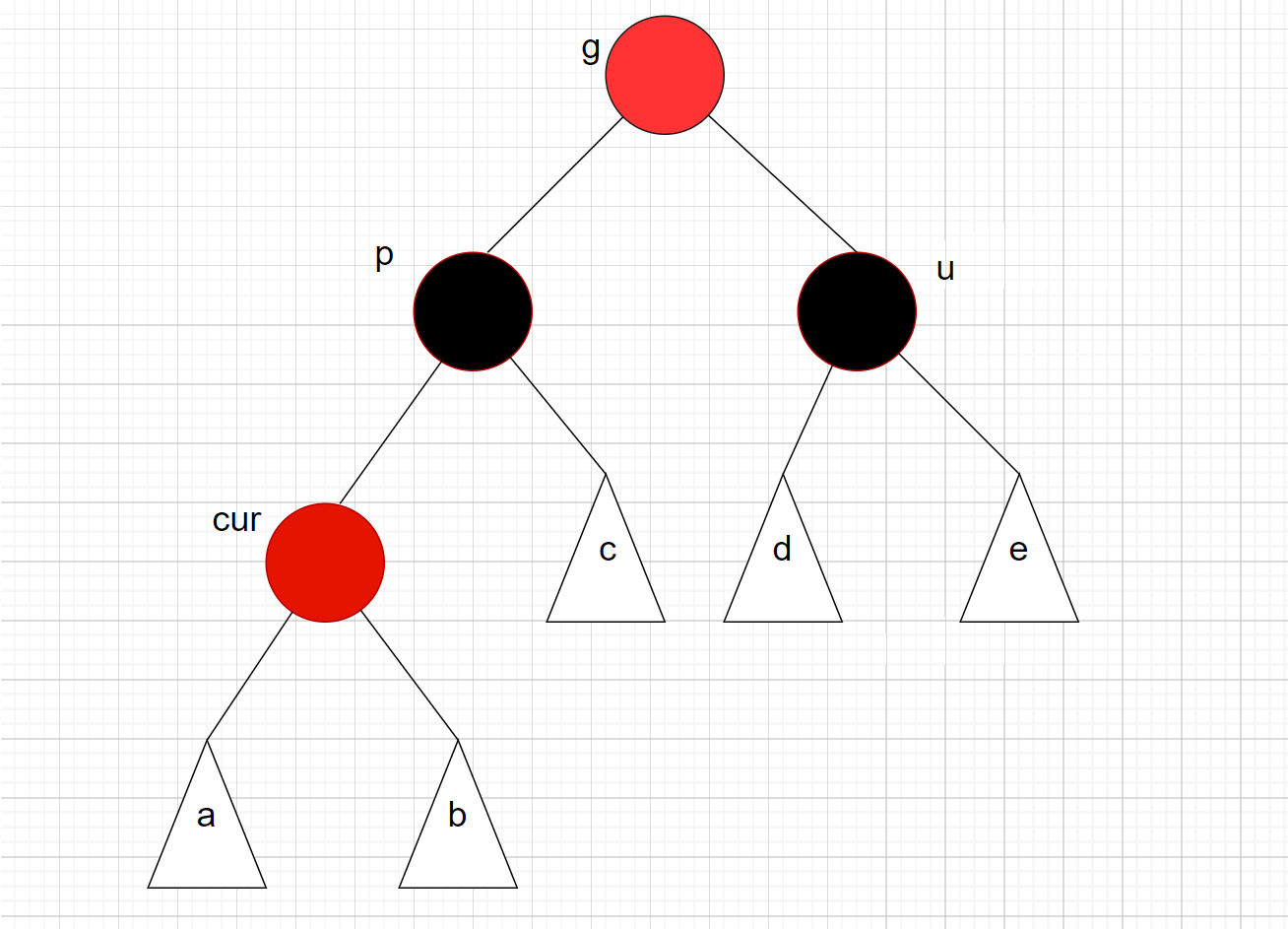
调整完以后,如果g是根节点, 需要将g改为黑色, 因为红黑树的性质规定根节点的颜色必须是黑色。
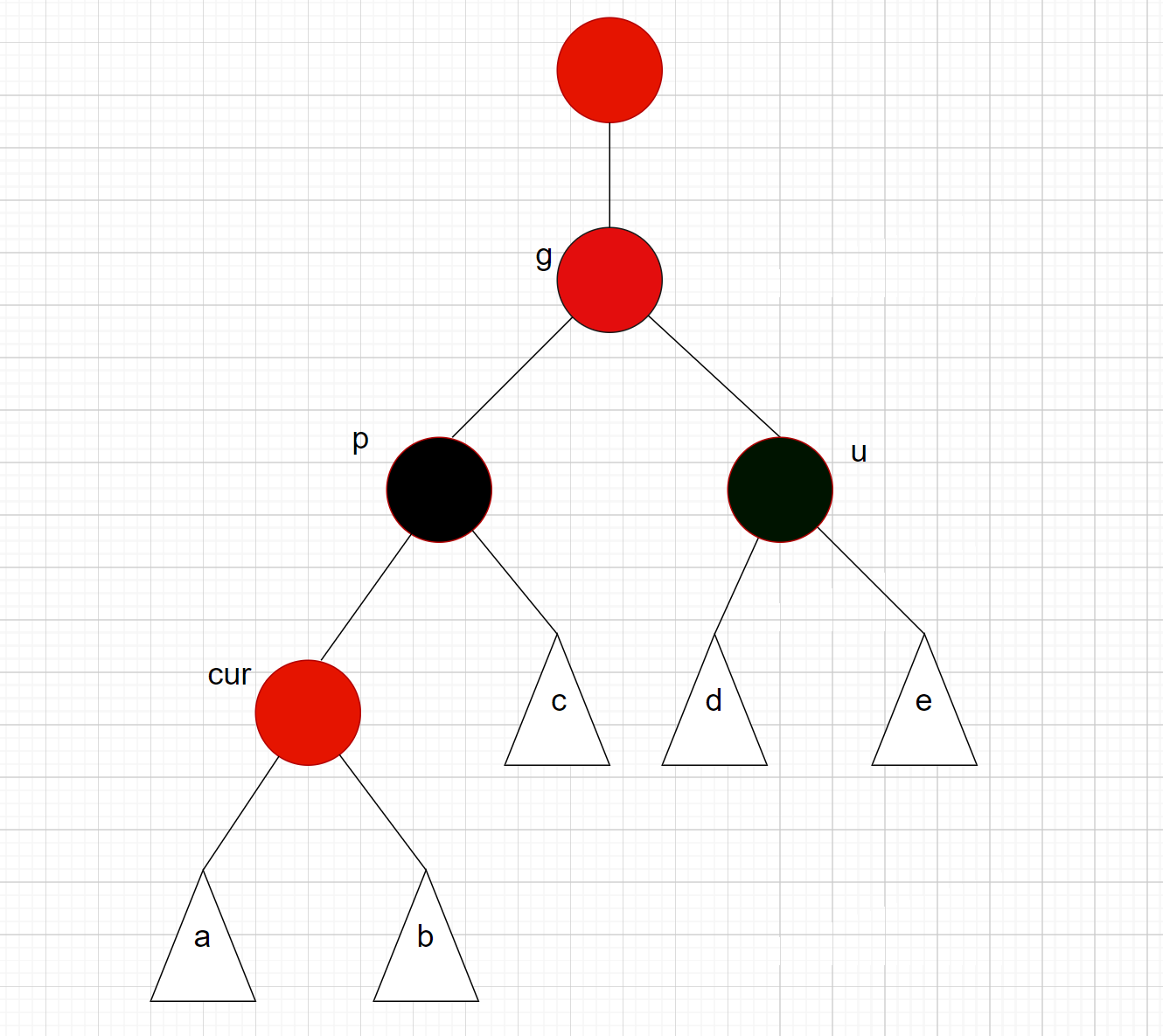
如果g是子树,并且g的双亲节点是红色的话就需要继续向上调整, 如下图所示:
4.2情况二: cur为红, p为红, g为黑, u不存在/u存在且为黑
这里说明u的情况有两种:
1.u不存在, 此时cur一定是新增节点, 如果cur不是新增节点的话, 那么cur和p一定有一个节点的颜色是黑色, 但是那样就不满足每条路径黑色节点的数目相同这一性质。
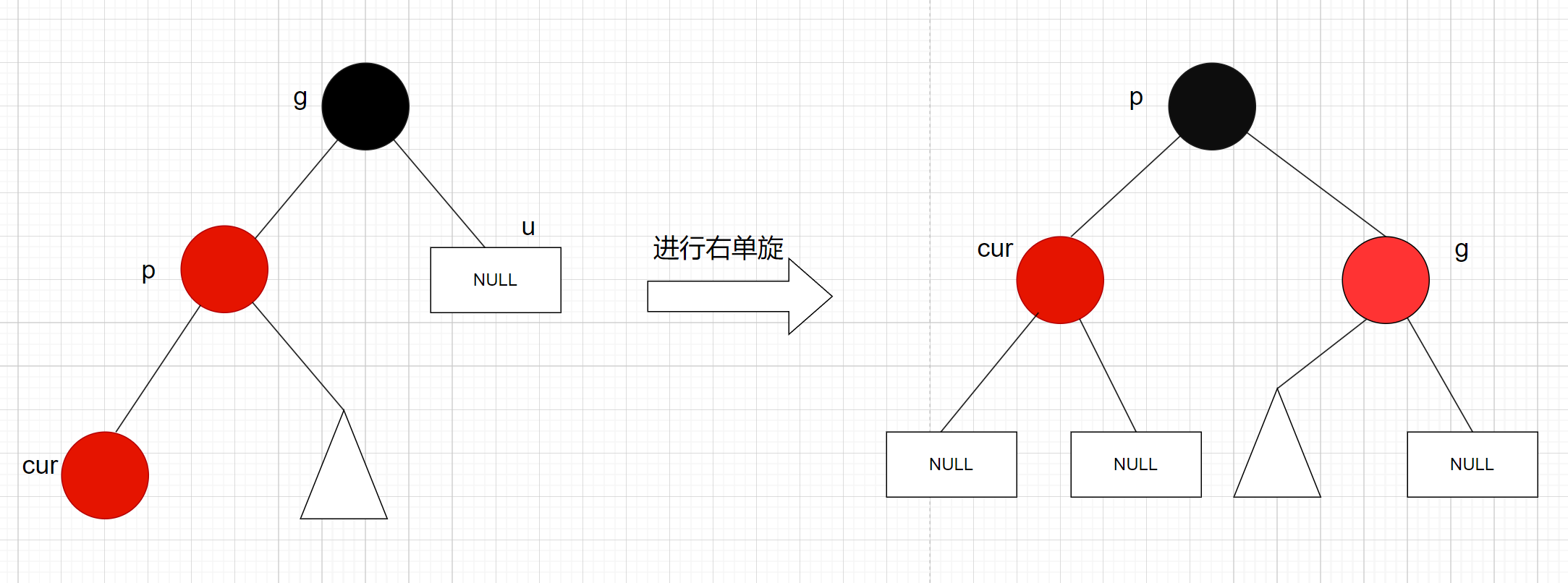
p是g的左子节点, cur是p的左子节点, 那么就对g进行右单旋:
变色处理:p, g变色 – p变黑色, g变红色
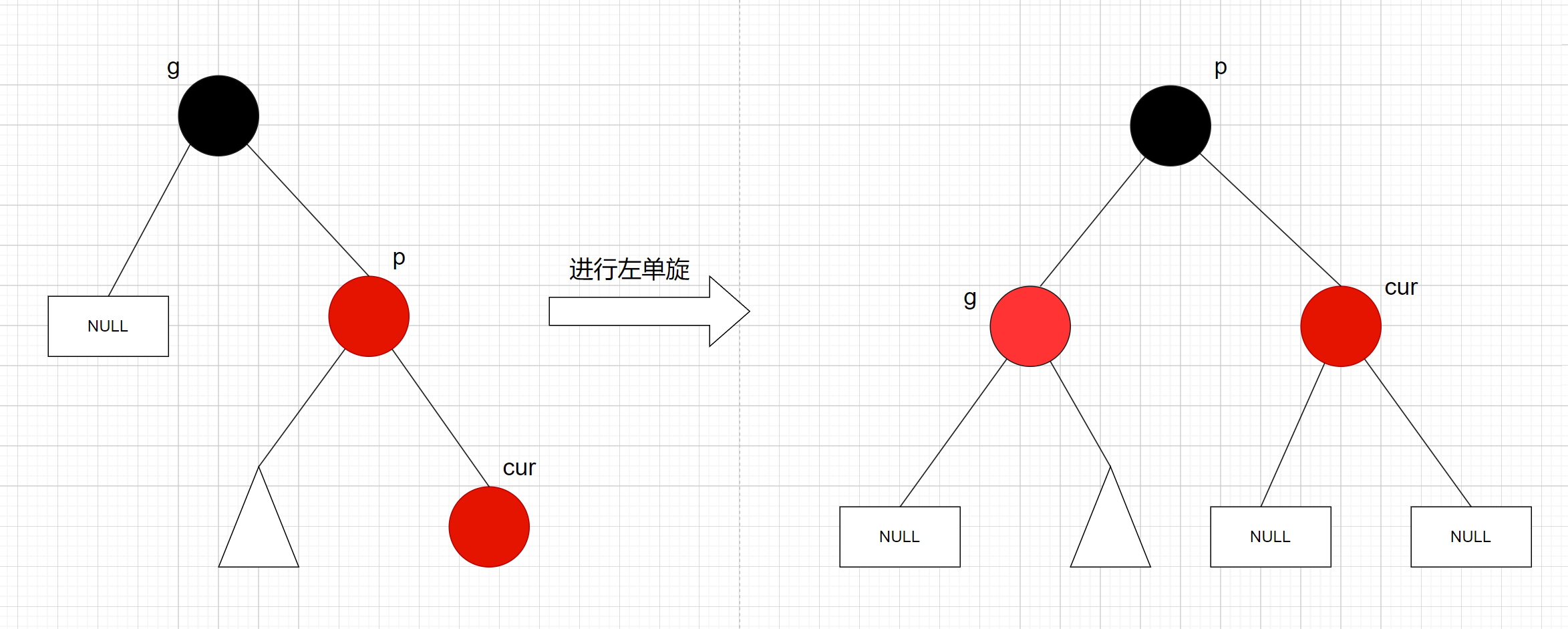
p是g的右子节点, cur是p的右子节点, 那么就对g进行左单旋:
变色处理:p, g变色 – p变黑色, g变红色
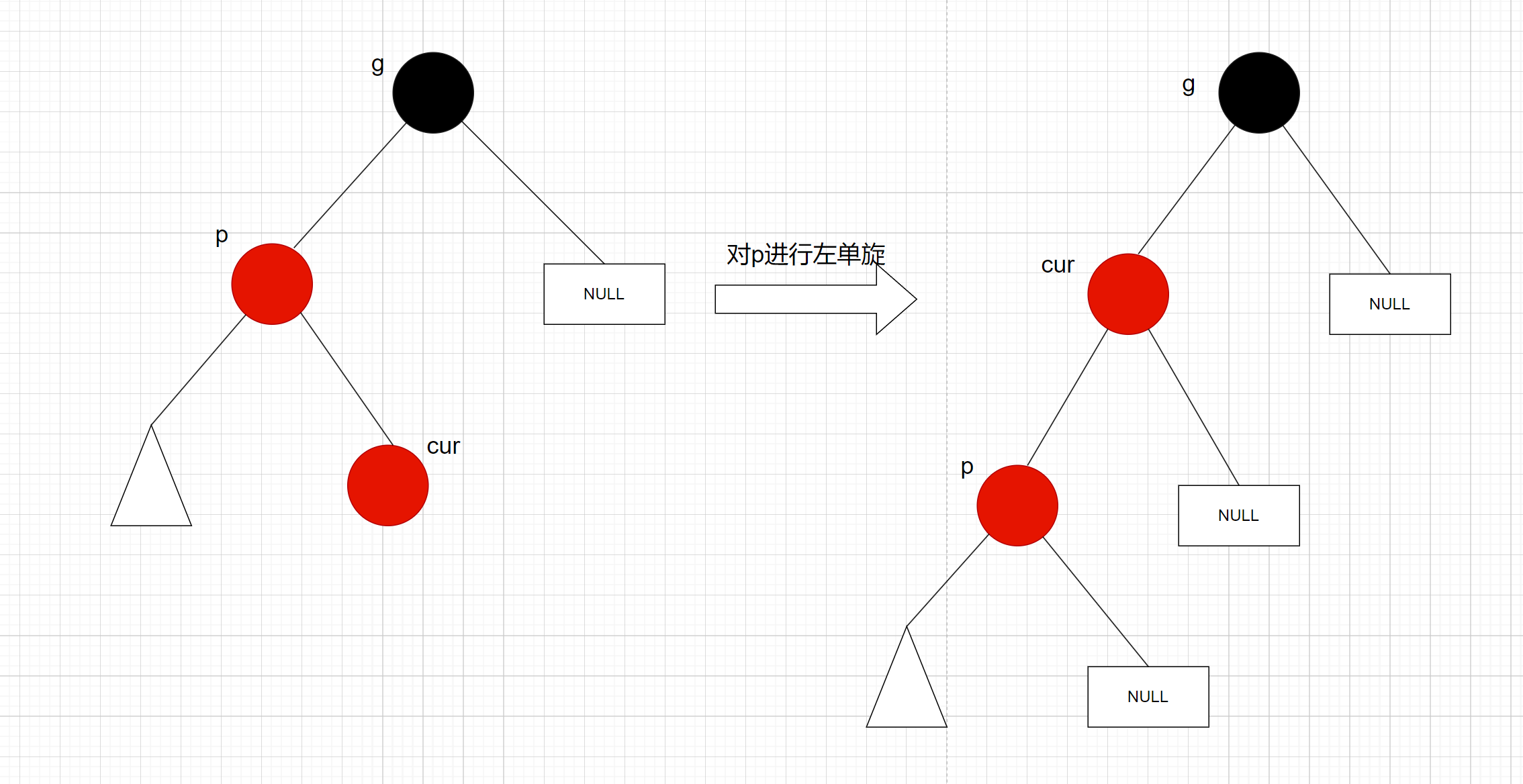
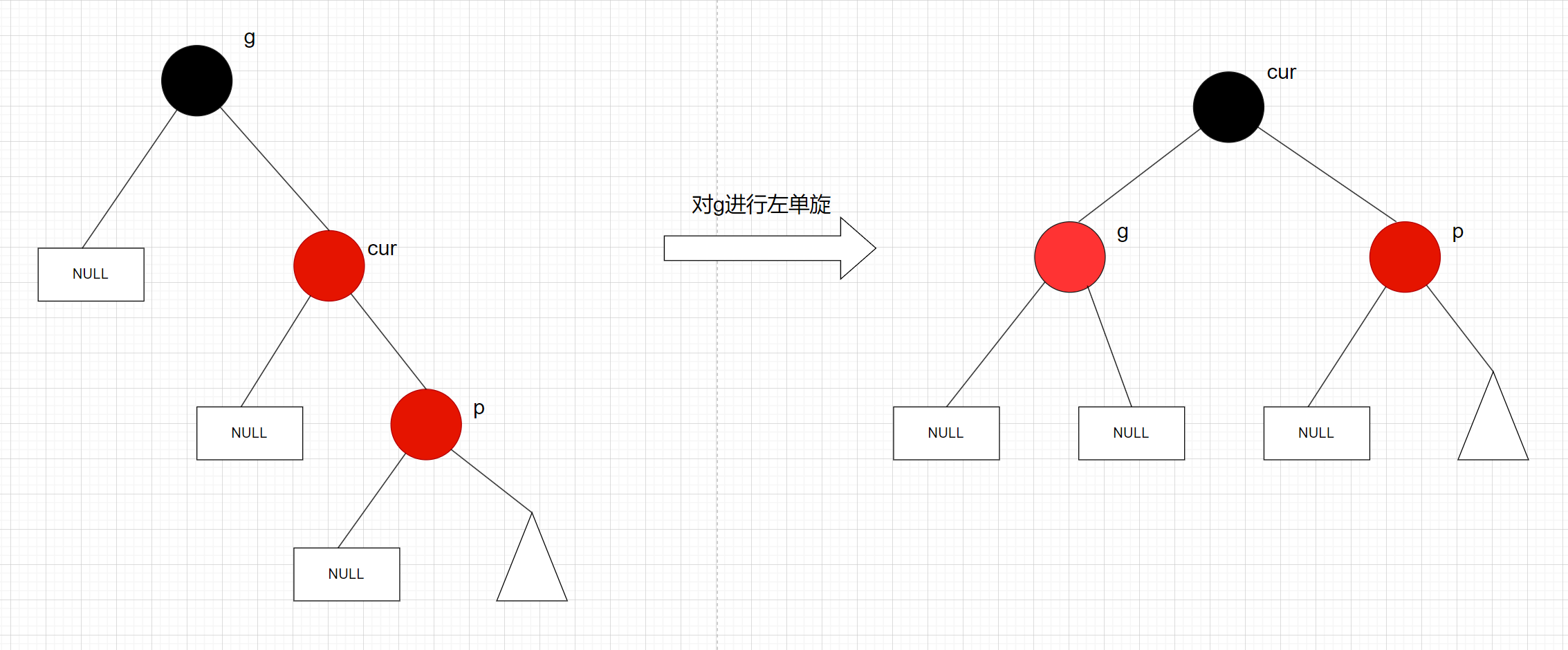
p是g的左子节点, cur是p的右子节点,先对p进行左单旋, 再对g做右单旋:
变色处理:cur, g变色 – cur变黑色, g变红色
先进行左单旋;
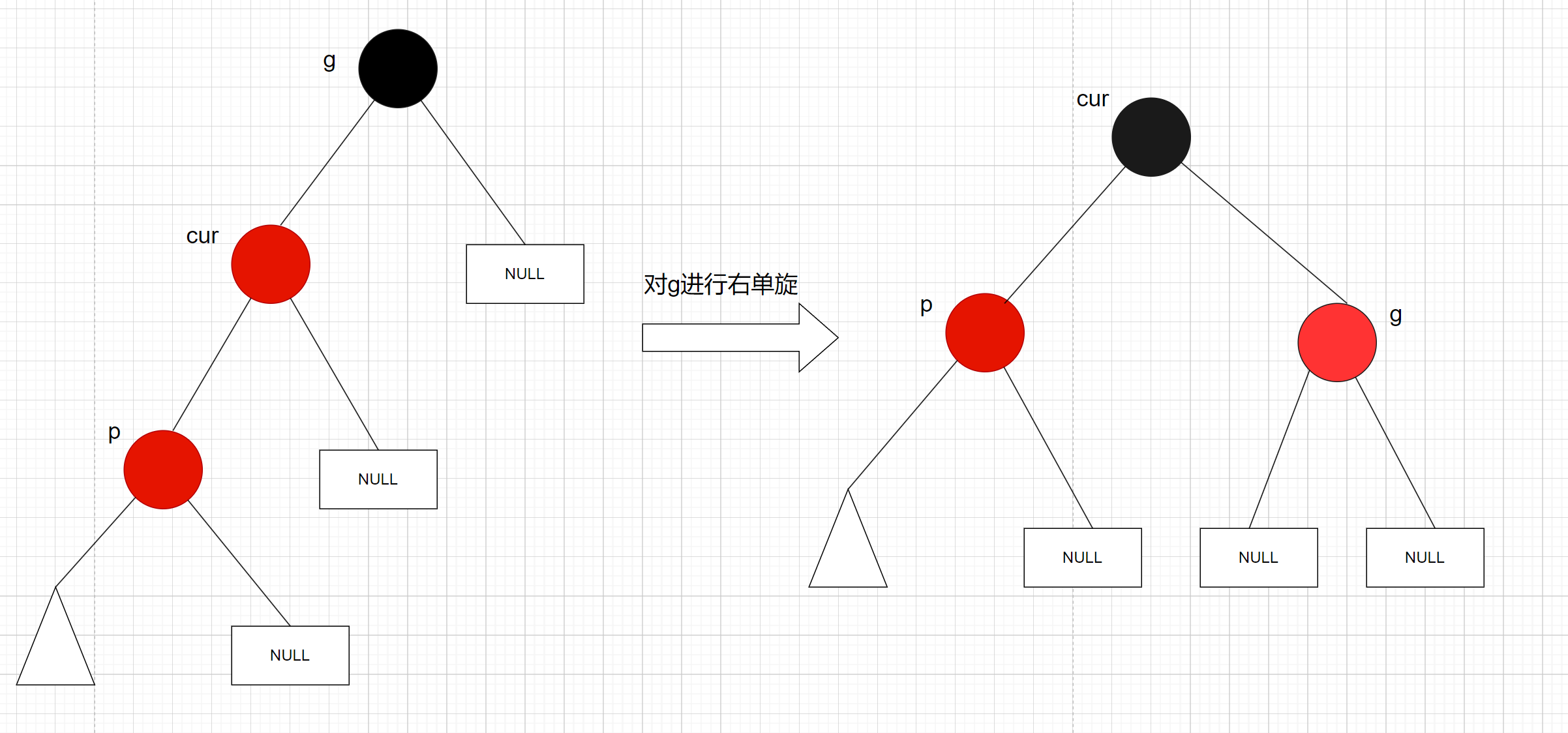
再进行右单旋:
p是g的右子节点, cur是p的左子节点, 先对p进行右单旋, 再对g进行左单旋:
变色处理:cur, g变色 – cur变黑色, g变红色
先进行右单旋:
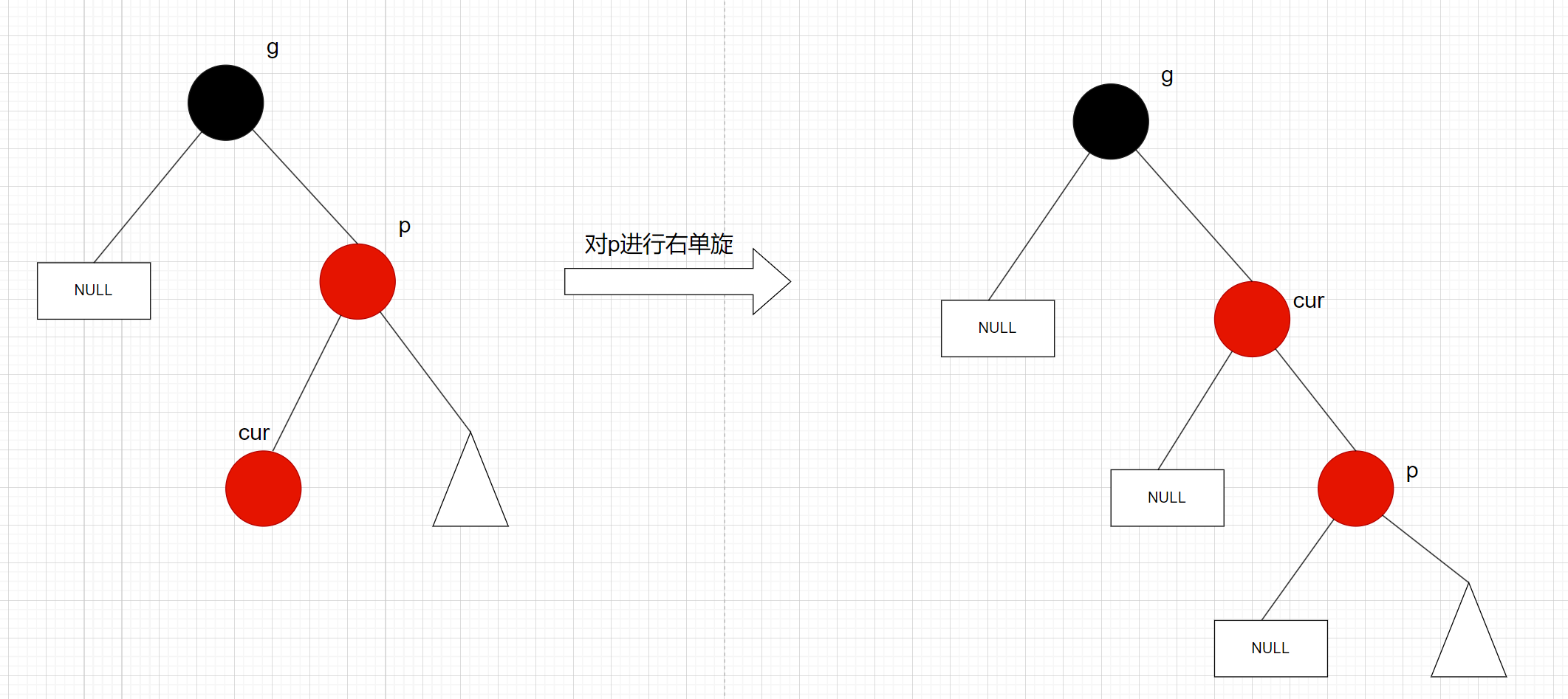
再进行左单旋:
2.u存在且为黑, 那么cur节点原来的颜色一定是黑色, 现在是红色的原因就是因为cur的子树在调整的过程中将cur的颜色更新成了红色。
p是g的左子节点, cur是p的左子节点, 那么就对g进行右单旋:
变色处理:p, g变色 – p变黑色, g变红色
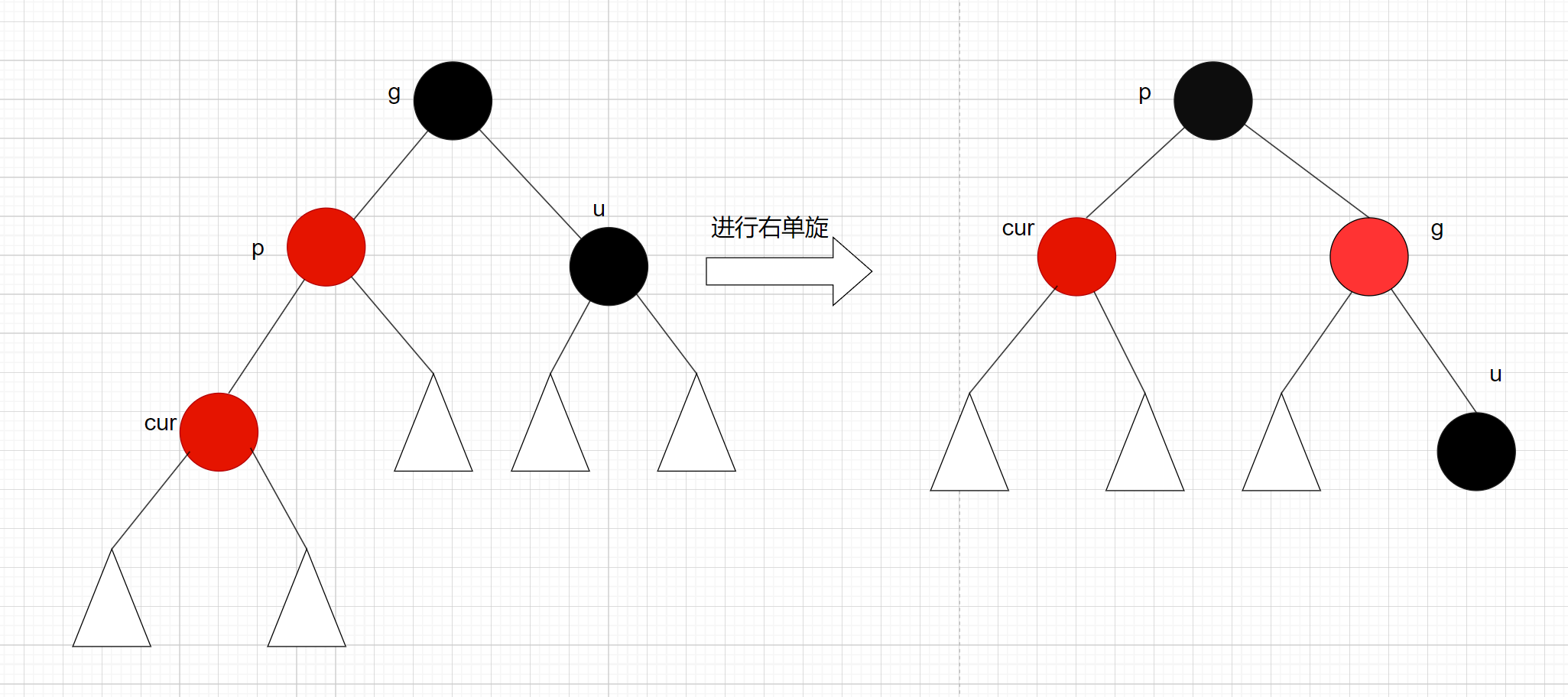
p是g的右子节点, cur是p的右子节点, 那么就对g进行左单旋:
变色处理:p, g变色 – p变黑色, g变红色
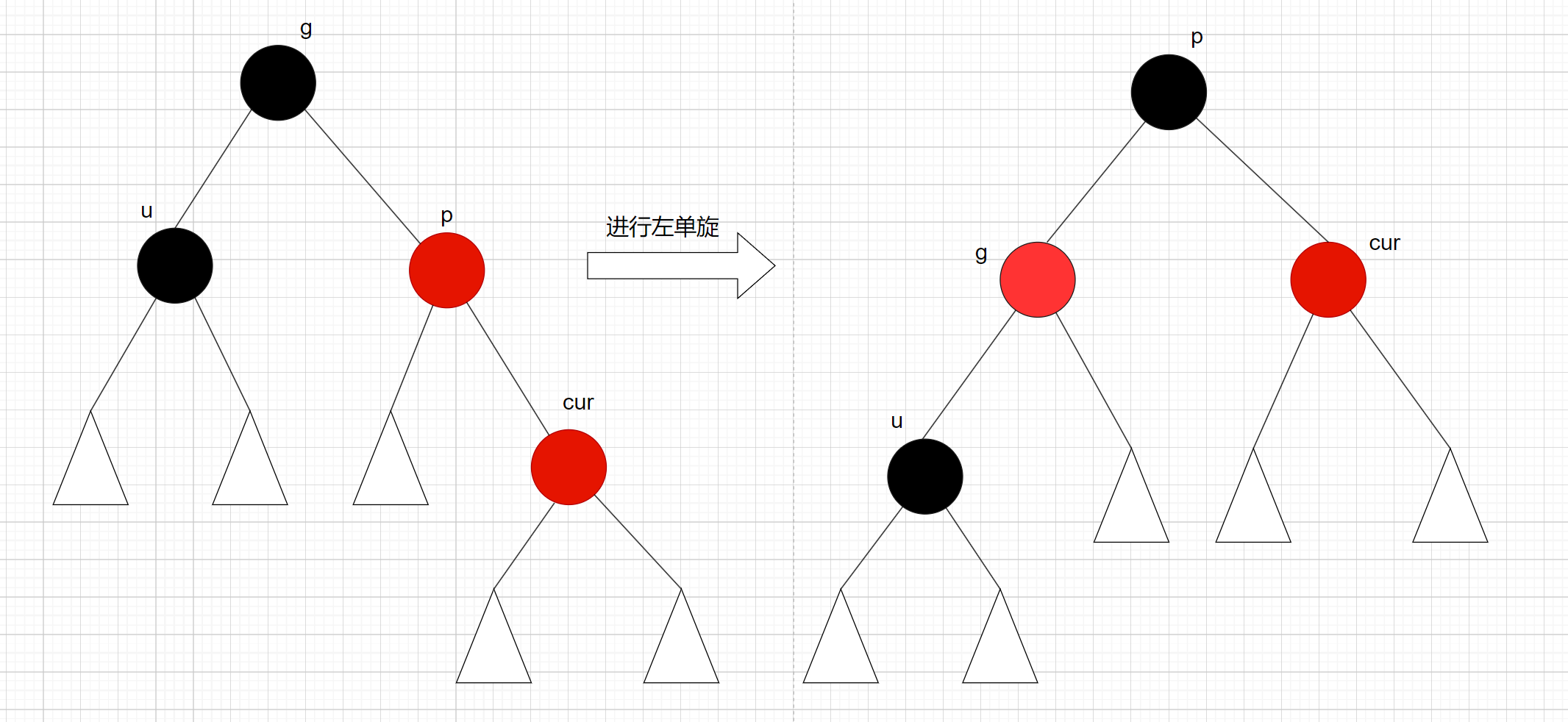
p是g的左子节点, cur是p的右子节点,先对p进行左单旋, 再对g做右单旋:
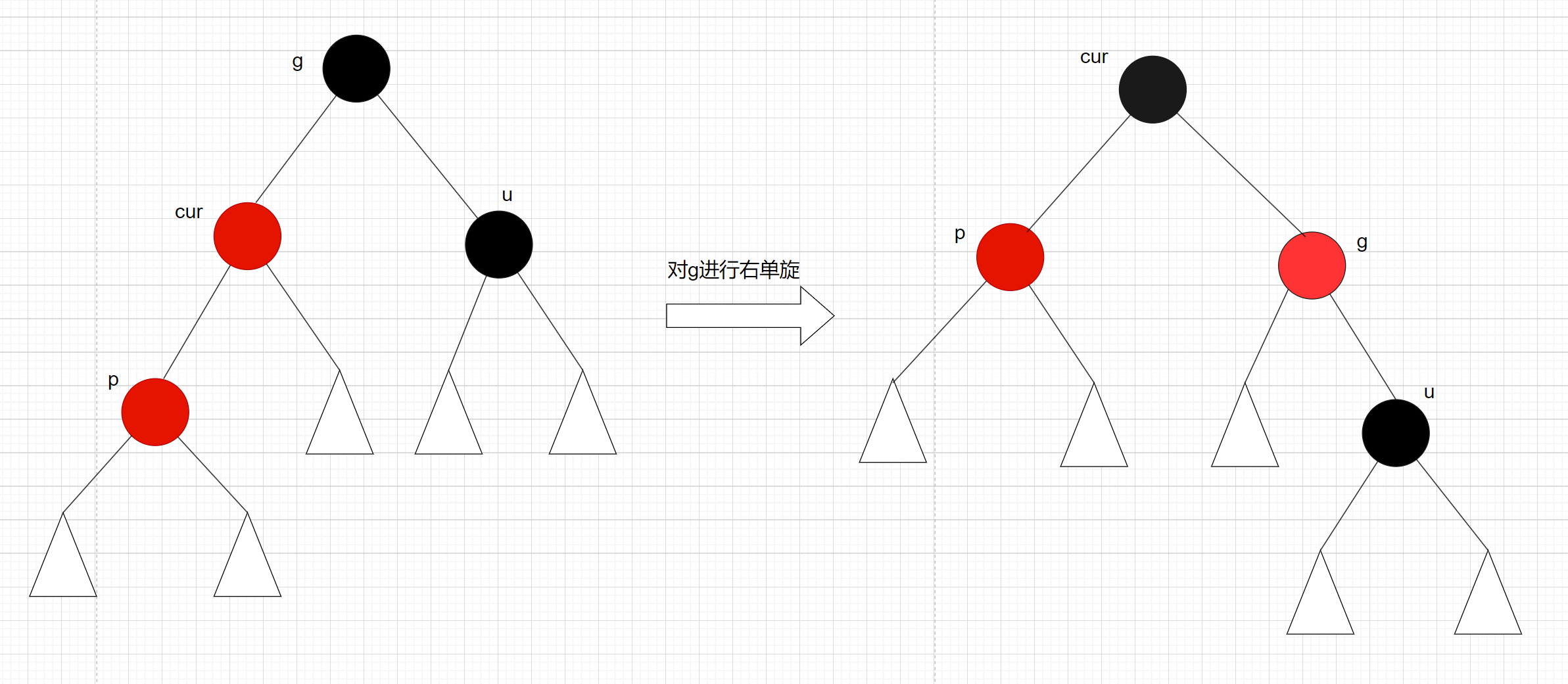
变色处理:cur, g变色 – cur变黑色, g变红色
先进行左单旋:
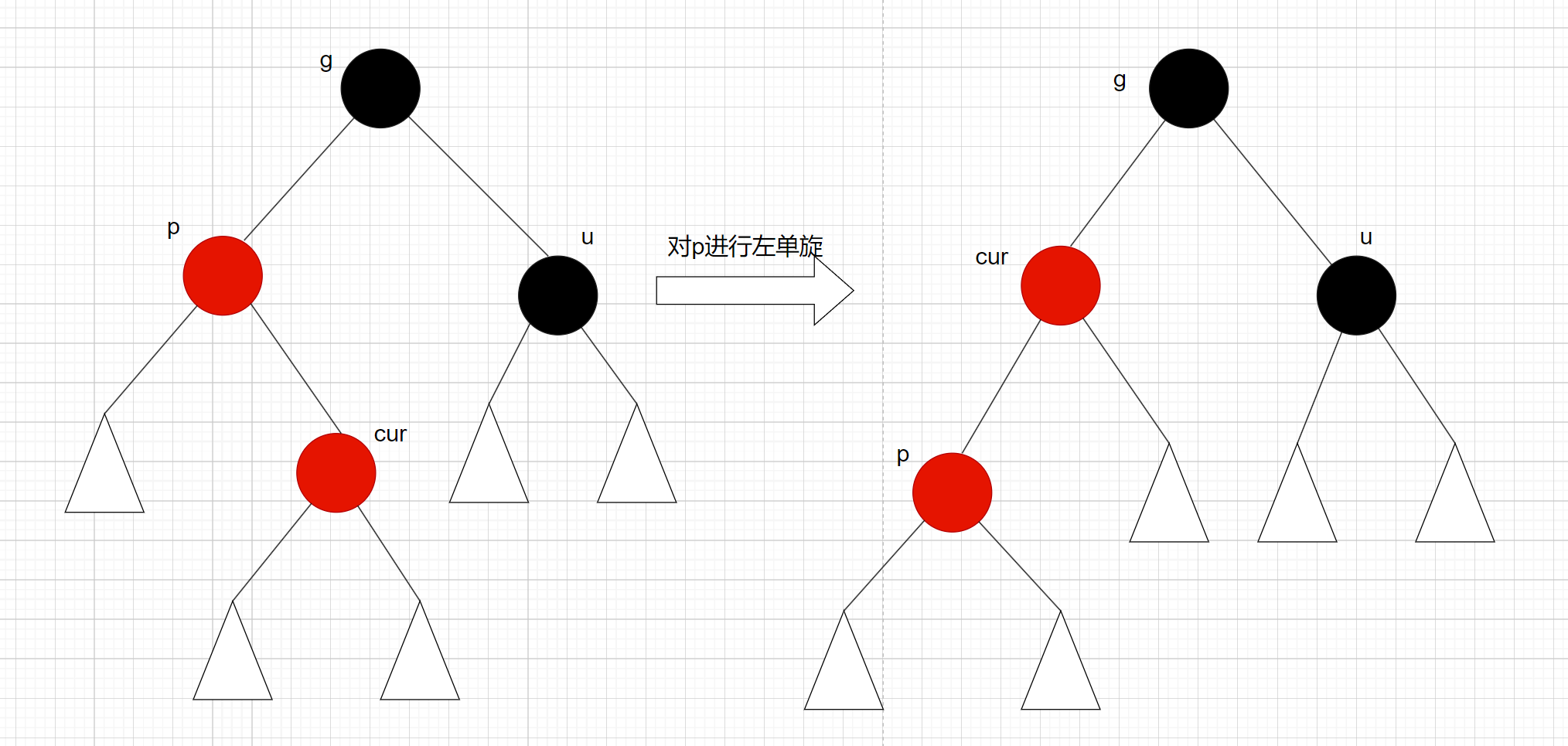
再进行右单旋:
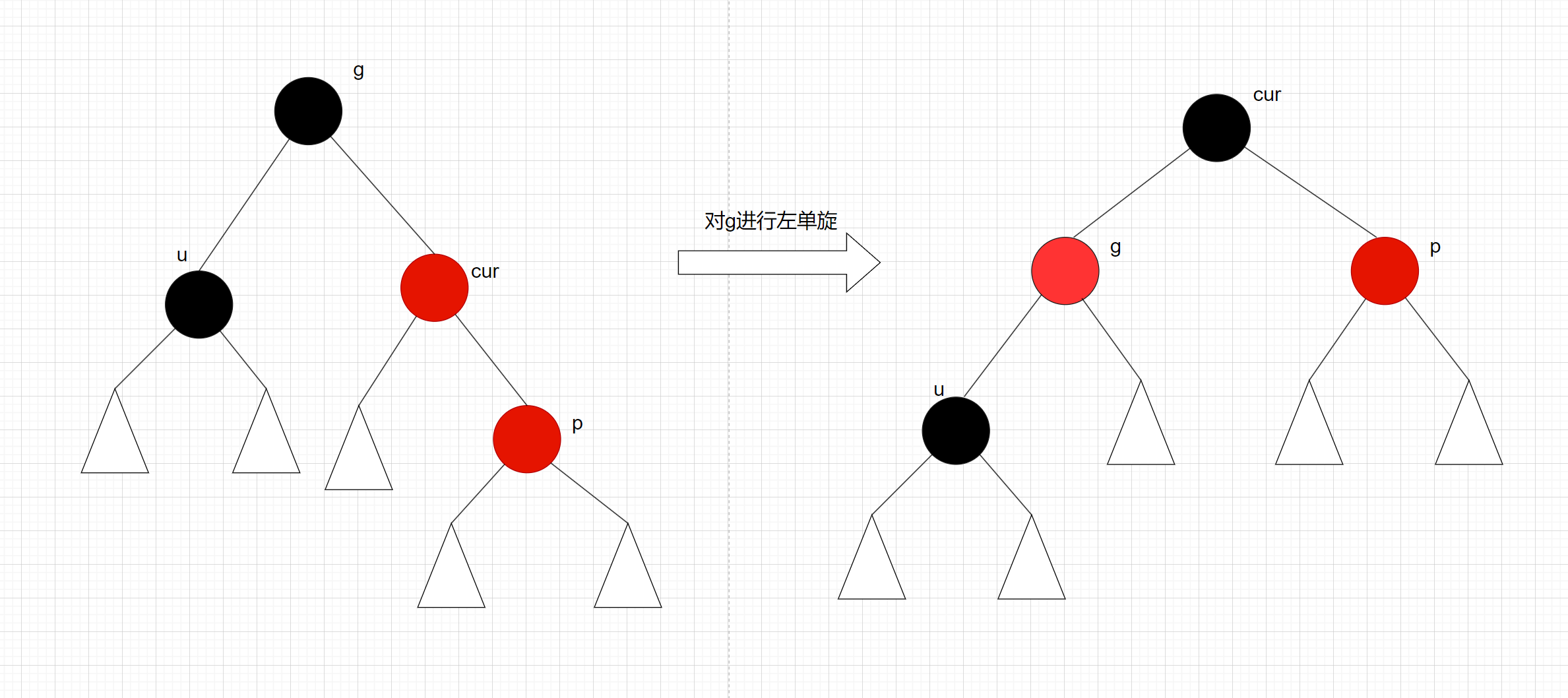
p是g的右子节点, cur是p的左子节点, 先对p进行右单旋, 再对g进行左单旋:
变色处理:cur, g变色 – cur变黑色, g变红色
先进行右单旋:
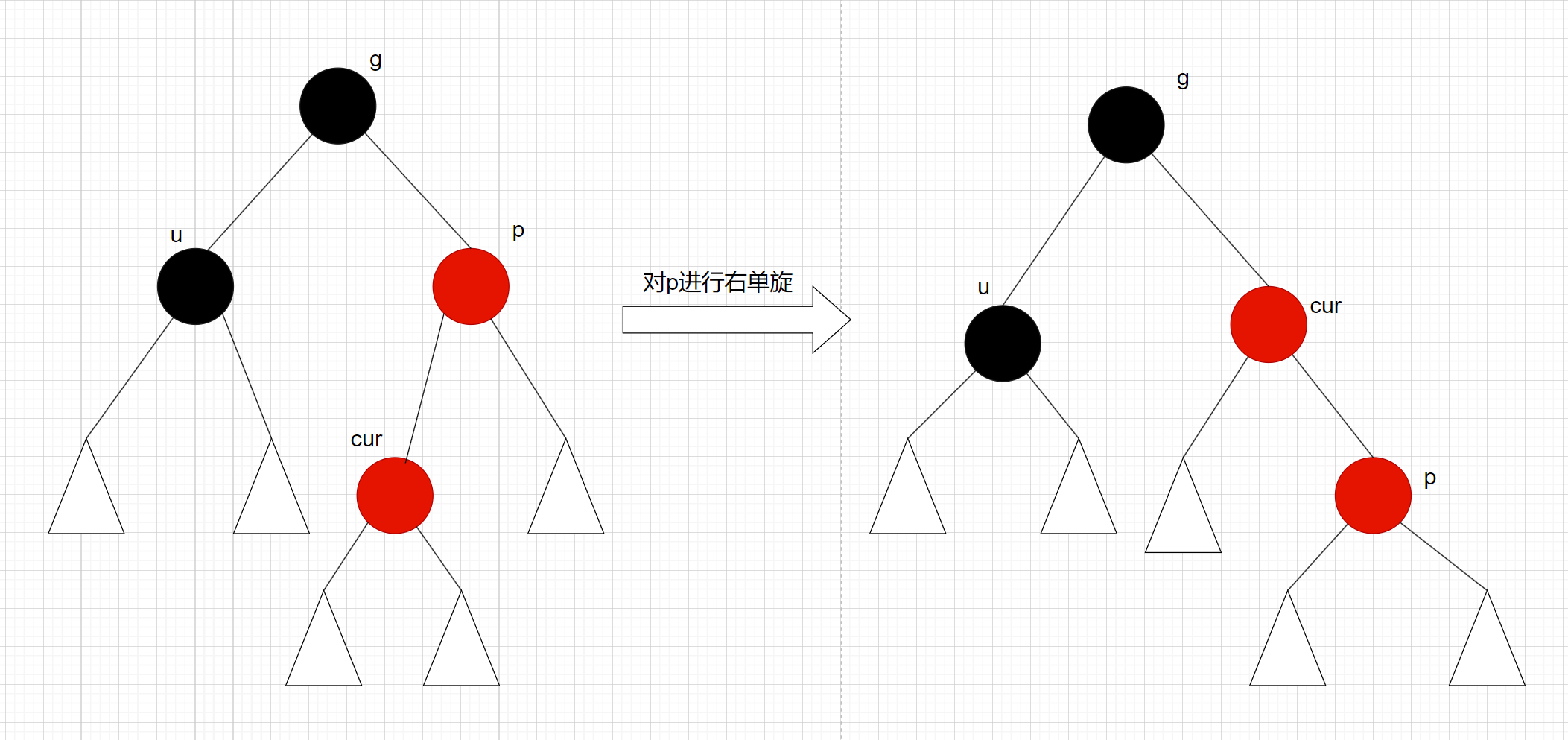
再进行左单旋:
左单旋代码实现:
//左单旋void RotateL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL){SubRL->_parent = parent;}Node* parentP = parent->_parent;SubR->_left = parent;parent->_parent = SubR;if (parentP == nullptr){_root = SubR;SubR->_parent = nullptr;}else{if (parentP->_left == parent){parentP->_left = SubR;SubR->_parent = parentP;}else{parentP->_right = SubR;SubR->_parent = parentP;}}}
右单旋代码实现:
//右单旋void RotateR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR)SubLR->_parent = parent;Node* parentP = parent->_parent;SubL->_right = parent;parent->_parent = SubL;if (parentP == nullptr){_root = SubL;SubL->_parent = nullptr;}else{if (parentP->_left == parent){parentP->_left = SubL;SubL->_parent = parentP;}else{parentP->_right = SubL;SubL->_parent = parentP;}}}
插入函数整体代码实现:
bool Insert(const pair<K, V>& kv){if (_root == nullptr){//如果是个空树就将新节点作为根节点_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//处理while (parent && parent->_col == RED){Node* grandfather = parent->_parent;// g//p u结构if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){//变色处理parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑-》旋转加变色{if (cur == parent->_left){//cur为parent的左子结点时进行右旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){//cur为父亲的右子节点时对g进行左单旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//双旋 -》 右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}
五、红黑树相关接口的实现
查找函数的实现:
依旧是根据二叉搜索树的查找规则:
//查找函数Node* Find(const K& key){if (_root == nullptr)return nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}elsereturn cur;}return nullptr;}
容量高度相关:
返回有效节点个数:
//有效节点个数int Size(){_Size(_root);}int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}二叉树高度:
//平衡二叉树高度int Height(){_Height(_root);}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}
中序遍历:
//中序遍历void Inorder(){_inorder(_root);cout << endl;}void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_inorder(root->_right);}
六、红黑树的验证
我们要通过代码来验证我们所实现的红黑树是否是符合红黑树的性质的。
红黑树的验证分为以下两步:
- 验证其是否满足二叉搜索树也就是中序遍历是否有序
- 验证其是否满足红黑树的性质
验证代码:
1、验证是否为二叉搜索树:
//中序遍历void Inorder(){_inorder(_root);cout << endl;}void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_inorder(root->_right);}
2、验证是否满足红黑树的性质:
//判断是否为红黑树bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED){return false;}// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色节点的数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}
通过以上几段代码就能完成对我们实现的红黑树验证。
七、红黑树与AVL数的比较
红黑树和AVL树都是平衡二叉搜索树, 进行增删查改的操作时的时间复杂度都是O(logN), 红黑树不追求绝对平衡, AVL树追求绝对平衡,相对而言红黑树在维持平衡时的旋转次数要少于AVL树, 因此在经常进行插入和删除的结构中红黑树的性能一般要优于AVL树, 因此是实际中使用红黑树更多。
八、红黑树的应用
- C++ STL库中的map/set 、mutil_map/mutil_set的实现
- java库
- linux内核
不止以上三处使用, 这里仅是为了举例。
关于红黑树的介绍到这里就结束了, 希望大家通过这篇文章能都红黑树有一定的理解, 以下是红黑树的具体代码实现链接:
红黑树具体实现代码
相关文章:

C++:平衡二叉搜索树之红黑树
一、红黑树的概念 红黑树, 和AVL都是二叉搜索树, 红黑树通过在每个节点上增加一个储存位表示节点的颜色, 可以是RED或者BLACK, 通过任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树能够确保没有一条路径会比…...

CentOS 7 系统优化
CentOS 7 系统优化 1、配置YUM源 阿里云的YUM源配置: CentOS 7使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repoCentOS 8使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS…...

扫雷游戏——附源代码
扫雷游戏的源代码比较简单,不设计比较复杂的代码,主要是多个函数的组合,每个函数执行自己的功能,最终支持游戏的完成。 1.菜单 我们需要一个提醒信息来让用户进行选择。 void menu() {printf("***********************\n&…...
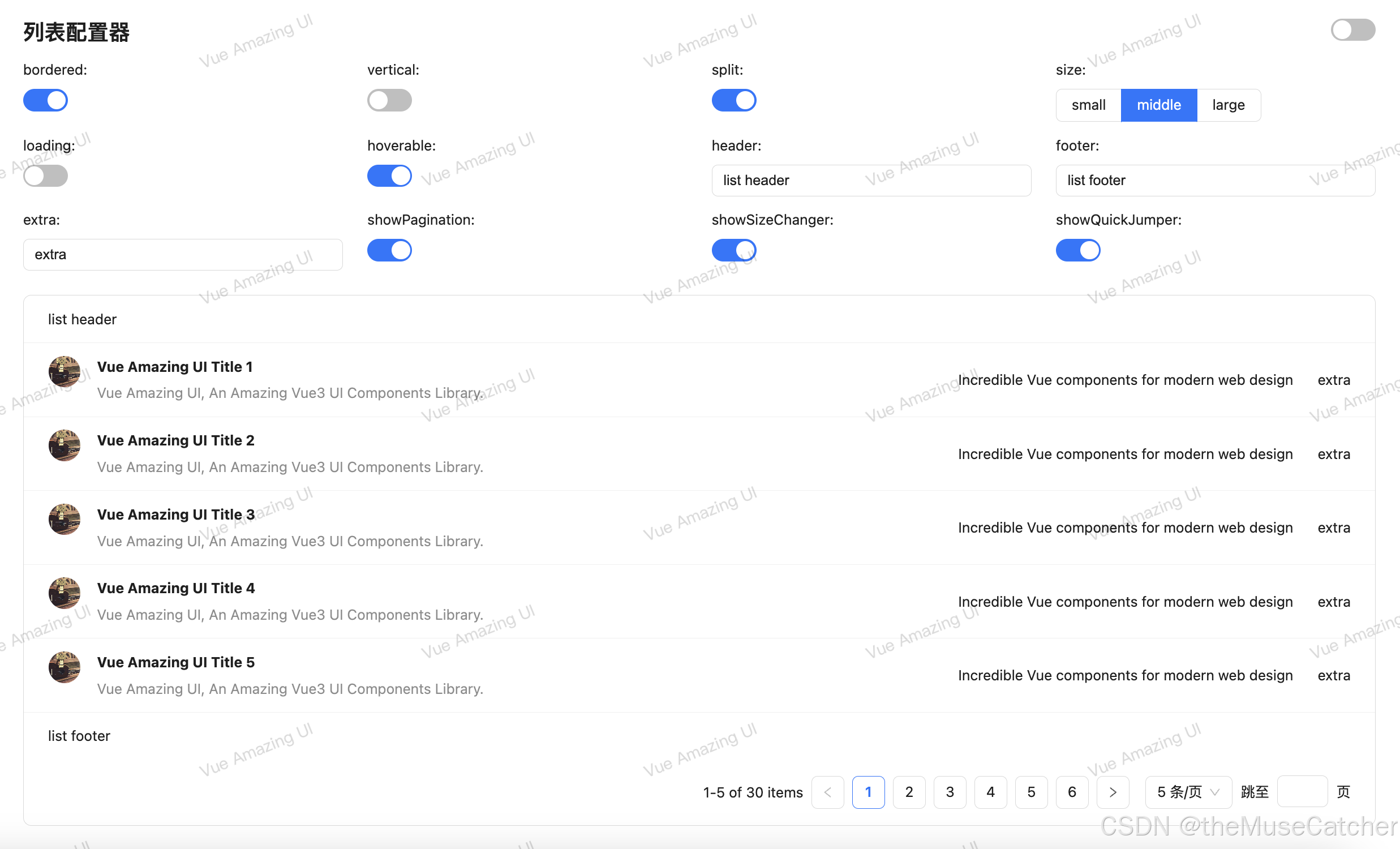
Vue3列表(List)
效果如下图:在线预览 APIs List 参数说明类型默认值bordered是否展示边框booleanfalsevertical是否使用竖直样式booleanfalsesplit是否展示分割线booleantruesize列表尺寸‘small’ | ‘middle’ | ‘large’‘middle’loading是否加载中booleanfalsehoverable是否…...

HarmonyOS NEXT - Navigation组件封装BaseNavigation
demo 地址: https://github.com/iotjin/JhHarmonyDemo 代码不定时更新,请前往github查看最新代码 在demo中这些组件和工具类都通过module实现了,具体可以参考HarmonyOS NEXT - 通过 module 模块化引用公共组件和utils 官方介绍 组件导航 (Navigation)(推…...
浅看MySQL数据库
有这么一句话:“一个不会数据库的程序员不是合格的程序员”。有点夸张,但是确是如此。透彻学习数据库是要学习好多知识,需要学的东西也是偏难的。我们今天来看数据库MySQL的一些简单基础东西,跟着小编一起来看一下吧。 什么是数据…...
)
Pytorch常用训练套路框架(CPU)
文章目录 1. 数据准备示例:加载 CIFAR-10 数据集 2. 模型定义示例:定义一个简单的卷积神经网络 3. 损失函数和优化器示例:定义损失函数和优化器 4. 训练循环示例:训练循环 5. 评估和测试示例:评估模型 6. 保存和加载模…...

C++ | Leetcode C++题解之第338题比特位计数
题目: 题解: class Solution { public:vector<int> countBits(int n) {vector<int> bits(n 1);for (int i 1; i < n; i) {bits[i] bits[i & (i - 1)] 1;}return bits;} };...
智慧校园云平台电子班牌系统源码,智慧教育一体化云解决方案
智慧校园云平台电子班牌系统,利用先进的云计算技术,将教育信息化资源和教学管理系统进行有效整合,实现生态基础数据共享、应用生态统一管理,为智慧教育建设的统一性,稳定性,可扩展性,互通性提供…...

数据库系统 第17节 数据仓库 案例赏析
下面我将通过几个具体的案例来说明数据仓库如何在不同的行业中发挥作用,并解决实际业务问题。 案例 1: 零售业 背景: 一家大型零售商希望改进其库存管理和市场营销策略,以提高销售额和顾客满意度。 解决方案: 数据仓库: 构建一个数据仓库࿰…...
硬件面试经典 100 题(71~90 题)
71、请问下图电路的作用是什么? 该电路实现 IIC 信号的电平转换(3.3V 和 5V 电平转换),并且是双向通信的。 上下两路是一样的,只分析 SDA 一路: 1) 从左到右通信(SDA2 为输入状态&…...

【git】代理相关
问题: 开启了翻墙代理工具,拉取代码时报错:fatal: 无法访问 xxxx : Failed to connect to github.com port 443: 连接超时 解决: 0,取消代理仍然无法拉取 1,查看控制面板-网络与Internet-代理ÿ…...
方式和闭包函数方式定义gin中间件)
golang gin框架中创建自定义中间件的2种方式总结 - func(*gin.Context)方式和闭包函数方式定义gin中间件
在gin框架中,我们可以通过2种方式创建自定义中间件: 1. 直接定义一个类型为 func(*gin.Context)的函数或者方法 这种方式是我们常用的方式,也就是定义一个参数为*gin.Context的函数或者方法。定义的方法就是创建一个 参数类型为 gin.Handler…...

Linux高级编程 8.13 文件IO
一、文件IO 操作系统为了方便用户使用系统功能而对外提供的一组系统函数。称之为 系统调用(unistd.h) 其中有个 文件IO,一般都是对设备文件操作,当然也可以对普通文件进行操作。 这是一个基于Linux内核的没有缓存的IO机制 文件IO特性&…...

【k8s】ubuntu18.04 containerd 手动从1.7.15 换为1.7.20
ubutnu18.04之前手动安装了1.7.15现在下载1.7.20containerd-1.7.20-linux-amd64.tar.gz root@k8s-worker-i58265u:/home/zhangbin# root@k8s-worker-i58265u:/home/zhangbin# https://github.com/containerd/containerd/releases/download/v1.7.20/containerd-1.7.20-linux-am…...

常用浮动方式
目录 一、标准流 二、float浮动 三、 flex浮动 3.1flex组成 3.2 主轴对齐方式 3.3侧轴对齐方式 3.4修改主轴方向 3.5弹性盒子换行 3.6行对齐方式 一、标准流 标签在网页中的默认排布规则 例如: 块元素独占一行、行内元素可以一行显示多个 二、float浮动 让块…...

设计模式反模式:UML常见误用案例分析
文章目录 设计模式反模式:UML常见误用案例分析1. 反模式概述2. 反模式的 UML 图示误用2.1 God Object 反模式2.2 Spaghetti Code 反模式2.3 Golden Hammer 反模式2.4 Poltergeist 反模式 3. 总结 设计模式反模式:UML常见误用案例分析 在软件工程领域&am…...

Python编码系列—Python SQL与NoSQL数据库交互:深入探索与实战应用
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...

贪心算法---跳跃游戏
题目: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 思路…...
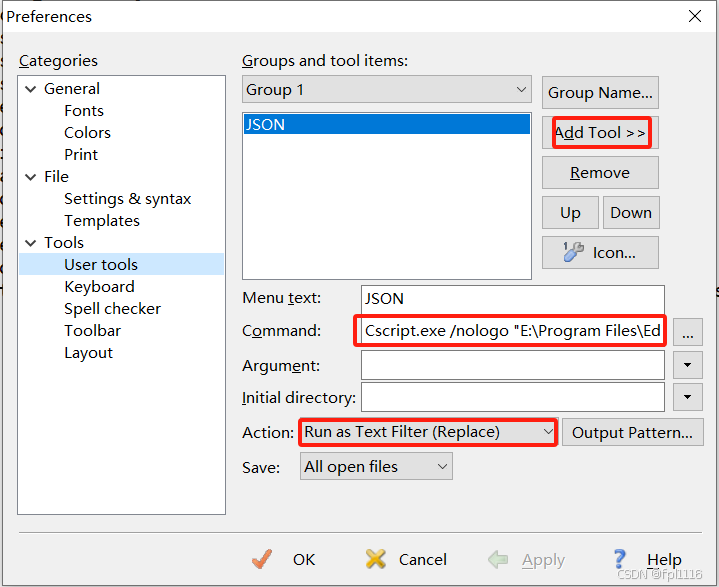
利用EditPlus进行Json数据格式化
利用EditPlus进行Json数据格式化 git下载地址:https://github.com/michael-deve/CommonData-EditPlusTools.git (安装过editplus的直接将里面的json.js文件复制走就行) 命令:Cscript.exe /nologo “D:\Program Files (x86)\EditPlus 3\json.js” D:\P…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
