数据结构—— 初识二叉树
1.树概念及结构
1.1树的概念
树是由根和子树构成
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的

1. 树有一个特殊的结点,称为根结点,根结点就是第一个节点
2. 除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个子节点
3. 树是递归定义的
4.在树形结构中,子树之间不能有交集,否则就不是树

1.2 树的相关概念

节点的度:一个节点含有的子树的个数称为该节点的度:如上图:A的为6(A B C D E F G)
重要部分:
* 叶节点或终端节点:子节点为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
* 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等结点为分支节点
* 双亲结点或父结点:若一个结点含有子结点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
* 孩子节点或子节点:一个节点含有的子树的根节点称为该结点的子结点; 如上图:B是A的孩子节点
* 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4

了解一下:
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6(A B C D E F G)

结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
堂兄弟结点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有节点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林(并查集,文件系统)
1.3 树的表示方法
树结构存储表示起来比较麻烦,既然保存值域,也要保存结点和结点之间
这里使用 "左孩子右兄弟 "表示法(子节点和兄弟节点)
也就是说不管有多少个孩子,每个节点只指向第一个孩子

1.A指向子节点B,A没有兄弟节点,指向空
2.B指向子节点D,B指向兄弟节点C,C没有兄弟节点,指向空
3.D没有子节点,D指向兄弟节点E,E指向兄弟节点F,F没有兄弟节点,指向空
4.E指向子节点H,H指向兄弟节点I,I没有兄弟节点,指向空
struct TreeNode
{int val;struct Node* leftchild;struct Node* rightBrother;};2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根结点加上两棵别称为左子树和右子树的二叉树组成
3. 二叉树不存在度大于2的结点
4.二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树

2.2 特殊的二叉树:
1. 满二叉树:每一个层的节点数都达到最大值,则这个二叉树就是满二叉树
也就是说,如果一棵二叉树的层数为K,且结点总数是(2^k - 1),则它就是满二叉树

2. 完全二叉树:前h-1层都是满的,最后一层不是满的,最后一层从左到右必须是连续的,如果不是连续的那么就不是完全二叉树
连续的:

不连续的:

满二叉树是一种特殊的完全二叉树,但是完全二叉树不是满二叉树
2.3 满二叉树和完全二叉树的位置计算
假设父节点在数组中的下标为i,那么:
1.左孩子在数组中的下标为:2*i+1
2.右孩子在数组中的下标为:2*i+2
假设孩子在数组中的下标为i,那么:
父在数组中的下标为:(i - 1)/ 2
在这里不区分左孩子和右孩子,因为除以会向下取整


3. 堆的概念及结构
3.1
1. 堆中某个结点的值总是不大于或不小于其父结点的值
2. 堆在逻辑上是一棵完全二叉树,物理上就是数组
3. 堆分为小堆和大堆
大堆:a. 完全二叉树
b. 任何一个父亲 > = 儿子
特点:根是最小

小堆: a. 完全二叉树
b. 任何一个父亲 < = 儿子
特点:根是最大

3.2 堆的实现
Heap.h
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;//堆的初始化
void HPInit(HP* php);//堆的销毁
void HPDestroy(HP* php);//堆的插入
void HPPush(HP* php, HPDataType x);//堆的删除
void HPPop(HP* php);// 取堆顶的数据
HPDataType HPTop(HP* php);//堆的判空
bool HPEmpty(HP* php);void Swap(HPDataType* p1, HPDataType* p2);void AdjustUp(HPDataType* a, int child);void AdjustDown(HPDataType* a, int n, int parent);Heap.c分解分析
堆的初始化
//堆的初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}堆的销毁
//堆的销毁
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}堆的插入
//堆的插入
void HPPush(HP* php, HPDataType x)
{assert(php);//判断内存是否满if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newcapacity;}//插入数据php->a[php->size] = x;php->size++;//插入数据之后需要向上调整AdjustUp(php->a, php->size - 1);
}堆的插入逻辑交换图表(向上调整)

堆的插入数据之后是否向上调整
//堆的插入数据之后是否向上调整
void AdjustUp(HPDataType* a, int child)
{//孩子/2找到父节点int parent = (child - 1) / 2;//孩子大于0就进入/继续while (child > 0){//如果孩子小于父亲if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交换child = parent;parent = (child - 1) / 2;}else{break;}}
}堆的交换
//堆的交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}堆的删除:一般是删除根
思路:排序删除:交换根和最后一个子节点的位置,再删除根,之后再进行向下调整算法(向下调整的前提是左右子树都是大小堆),然后根据左右子树的大小选择小的那个进行调整

//堆的删除
void HPPop(HP* php)
{assert(php);assert(php->size > 0);//交换下标为0的根和末尾数据的位置Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//删除//向下调整AdjustDown(php->a, php->size, 0);
}堆的向下调整
思路:先假设左孩子小,然后找出小的那个孩子,再判断右孩子是否小于n并且右孩子小于左孩子
向下调整的前提是左右子树都是大小堆
//堆的向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{// 先假设左孩子小int child = parent * 2 + 1;// child >= n说明孩子不存在,调整到叶子了while (child < n) {// 找出小的那个孩子//判断右孩子是否小于n并且右孩子小于左孩子 if (child + 1 < n && a[child + 1] < a[child]){++child;}//if (a[child] > a[parent]) 大堆//孩子小于父亲if (a[child] < a[parent])//小堆{//交换Swap(&a[child], &a[parent]);parent = child;//赋予//继续算左孩子child = parent * 2 + 1;}else{break;}
}取堆顶的数据
// 取堆顶的数据
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}堆的判空
//堆的判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}Heap.c全部代码
#include"Heap.h"//堆的初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//堆的销毁
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}//堆的插入
void HPPush(HP* php, HPDataType x)
{assert(php);//判断内存是否满if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newcapacity;}//插入数据php->a[php->size] = x;php->size++;//插入数据之后需要向上调整AdjustUp(php->a, php->size - 1);
}//堆的插入数据之后是否向上调整
void AdjustUp(HPDataType* a, int child)
{//孩子/2找到父节点int parent = (child - 1) / 2;//孩子大于0就进入/继续while (child > 0){//如果孩子小于父亲if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交换child = parent;parent = (child - 1) / 2;}else{break;}}
}//堆的交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//堆的删除
void HPPop(HP* php)
{assert(php);assert(php->size > 0);//交换下标为0的根和末尾数据的位置Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//删除//向下调整AdjustDown(php->a, php->size, 0);
}//堆的向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{// 先假设左孩子小int child = parent * 2 + 1;// child >= n说明孩子不存在,调整到叶子了while (child < n) {// 找出小的那个孩子//判断右孩子是否小于n并且右孩子小于左孩子 if (child + 1 < n && a[child + 1] < a[child]){++child;}//if (a[child] > a[parent]) 大堆//孩子小于父亲if (a[child] < a[parent])//小堆{//交换Swap(&a[child], &a[parent]);parent = child;//赋予//继续算左孩子child = parent * 2 + 1;}else{break;}}
}// 取堆顶的数据
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//堆的判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}感谢观看~
相关文章:

数据结构—— 初识二叉树
1.树概念及结构 1.1树的概念 树是由根和子树构成 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 1. 树有…...

2024.08.09校招 实习 内推 面经
地/球🌍 : neituijunsir 交* 流*裙 ,内推/实习/校招汇总表格 1、校招 | 顺丰科技 2025届秋季校园招聘技术专场正式启动(内推) 校招 | 顺丰科技 2025届秋季校园招聘技术专场正式启动(内推) …...

IDEA中设置类和方法的注释
分两步设置: 第一个设置是创建类的时候自动加的注解 第二个设置是快捷键为方法增加的注解 类的时候自动加的注解设置 注释模版 #if (${PACKAGE_NAME} && ${PACKAGE_NAME} ! "")package ${PACKAGE_NAME};#end /** * Description: TODO * Auth…...

Adobe Premiere Pro 2023-23.6.7.1 解锁版下载与安装教程 (一款专业的视频编辑软件)
前言 Adobe Premiere Pro(简称PR)是一款知名的专业视频编辑软件,数字视频剪辑软件。主要用来编辑视频和音频,可以在RGB和YUV色彩空间中以高达32位色彩的视频分辨率对4K和更高质量的视频文件进行编辑,支持VST音频插件和…...
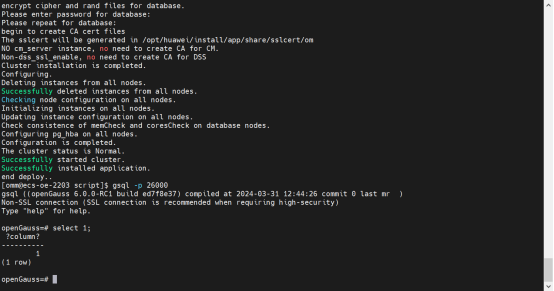
openGauss 6.0安装过程解除对root用户依赖之gs_preinstall
目录 1.执行前提条件 1.1设置OS参数: 1.2定时任务权限 1.3 修改最大文件描述符 2.切换至omm用户,执行preinstall 3.source环境变量 4.执行gs_install 在给客户部署业务系统时,由于openGauss数据库的预安装过程需要用到root用户执行&am…...

IOS 10 统一颜色管理和适配深色模式
实现分析 像系统那样,给项目中常用的颜色取名字,这里使用扩展语法实现,好处是可以像访问系统颜色那样访问自定义的颜色。 添加依赖 为了能使用16进制的颜色值,这里通过依赖DynamicColor框架来实现 #颜色工具类 #https://githu…...

Linux目录结构及基础查看命令和命令模式
Linux目录结构及基础查看命令和命令模式 1.树形目录结构根目录 所有分区、目录、文件等的位置起点整个树形目录结构中,使用独立的一个“/”表示 常见的子目录 /root 管理员的宿主(家)目录 /home/xxx 普通用户的家目录 /bin 命令文件目录,存放所…...

UDP和TCP协议段格式分析
目录 UDP协议 特点 UDP协议的缓冲区 UDP协议段格式 TCP协议 特点 如何理解TCP是传输控制协议? TCP协议段格式 四位首部长度 16位窗口大小 32位序号 32位确认序号 TCP/IP四层模型: UDP协议 UDP(User Datagram Protocol ÿ…...
)
Go语言基础--条件判断(if语句)
if语句它允许程序根据一个或多个条件(通常是布尔表达式)的真假来决定执行哪一段代码。如果条件为真(true),则执行if语句块内的代码;如果条件为假(false),则跳过该代码块&…...
应用)
白骑士的C#教学实战项目篇 4.2 图形用户界面(GUI)应用
系列目录 上一篇:白骑士的C#教学实战项目篇 4.1 控制台应用程序 在这一部分,我们将从简单的控制台应用程序过渡到图形用户界面(GUI)应用程序。GUI 应用程序更加直观和用户友好,是现代软件开发的核心内容。我们将介绍如…...

【Java学习】反射和枚举详解
所属专栏:Java学习 🍁1. 反射 在程序运行时,可以动态地创建对象、调用方法、访问和修改字段,以及获取类的各种属性信息(如成员变量、方法、构造函数等),这种机制就称为反射 反射相关的类 类名用…...

leetcode-461. 汉明距离
题目描述 两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。 给你两个整数 x 和 y,计算并返回它们之间的汉明距离。 示例 1: 输入:x 1, y 4 输出:2 解释: 1 (0 0 0 1) 4 (0 1 0 0) …...

rpmbuild 将二进制文件 strip,文件 md5 发生改变
rpmbuild 将二进制文件 strip,文件 md5 发生改变 上一篇中提到 strip 相关的操作,会去掉文件中的调试信息【strip 、objdump、objcopy 差异与区别】 在编译或打包环境中,莫名其妙的文件 大小 md5 都发生了改变,怀疑跟 rpmbuild 打…...

selenium爬取搜狗网站新闻的小Demo
使用之前请确保自己chrome浏览的版本与chromedriver的版本一致, Mac确保chromedriver已经放到python的bin目录中 Windows确保chromedriver已经放到python.exe同目录中 当前selenium Version: 3.141.0,4版本后面改为:find_element(By.CLASS_NA…...
)
R 语言学习教程,从入门到精通,R CSV 文件使用(17)
1、R CSV 文件 R 作为统计学专业工具,如果只能人工的导入和导出数据将使其功能变得没有意义,所以 R 支持批量的从主流的表格存储格式文件(例如 CSV、Excel、XML 等)中获取数据。 1.1、CSV 表格交互 CSV(Comma-Separ…...

【LLM之Base Model】Weaver论文阅读笔记
研究背景 当前的大型语言模型(LLM)如GPT-4等,尽管在普通文本生成中表现出色,但在创造性写作如小说、社交媒体内容等方面,往往不能很好地模仿人类的写作风格。这些模型在训练和对齐阶段,往往使用的是大规模…...

泰坦尼克号 - 从灾难中学习机器学习/Titanic - Machine Learning from Disaster(kaggle竞赛)第一集(了解赛题)
此次目的: hello大家好,俺是没事爱瞎捣鼓又分享欲爆棚的叶同学!!!准备出几期博客来记录我学习kaggle数据科学入门竞赛的过程,顺便也将其中所学习到的知识分享出来。这是第一集(了解赛题&#x…...

使用C++调用PyTorch模型的弯弯绕绕,推荐LibTorch加载,C++处理
需求:使用C调用Pytorch模型,对处理后的图像进行预测。 第一种,使用C调用Python代码处理,使用pybind11源代码再末尾 缺点,导入Python包非常麻烦,执行的C程序找不到cv2 torch包等等 本人解决了cv2 numpy等包&…...

实现异形(拱形)轮播图
项目需要实现如上图所示的轮播图。 实现思路: 1.项目引入使用普通轮播图。 2.根据轮播图个数,动态给可视范围的第一个轮播图和最后一个轮播图添加样式。 代码实现: 经调研,使用slick轮播图(官网地址 https://kenwheel…...

【软件测试】2024年职业院校技能大赛高职组“软件测试”赛项样题
目录 任务一:功能测试(45 分) 任务二:自动化测试(15 分) 任务三:性能测试(15 分) 任务四:单元测试(10 分) 任务五:接…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
